静态场景下HDFS副本放置的改进策略

鲍敬源，赵 宁，汪 洋

（1.海装武汉局驻武汉地区第二军事代表处，湖北武汉 430064；2.武汉理工大学计算机科学与技术学院，湖北 武汉 430070；3.贝壳找房科技有限公司，北京 100089）

0 引言

云存储系统［1-2］在大数据时代发挥着越来越重要的作用。作为云计算平台Hadoop 的存储模块，HDFS 采取了多副本记忆数据检测和快速恢复机制，其默认的副本放置策略为机架感知（rack-aware），即动态感知集群拓扑结构的变化，默认副本因子为3。该策略的缺点在于：没有充分考虑异构环境中各节点的差异（特别是在静态场景下对时间要求不高），没有根据节点情况充分优化放置策略。针对这一问题，本文提出静态场景下结合二进制灰狼优化算法的改进版多目标灰狼优化算法，以集群读取效率、整体负载均衡度、平均副本失效率为目标函数进行优化，减小了陷入局部最优的概率，增加了解的多样性，从而以一定时间成本得出在上述3 项指标上效果更好的方案。

1 相关工作

HDFS 副本放置分为静态和动态两种场景，前者即文件分批次处理，对时间要求不高，优化空间较大；后者的文件请求随机到达，请求频率和规律具有不确定性。

1.1 静态场景下的副本放置策略相关研究

此类场景通常是在集群上进行预定的计算任务，因而可以提前获得如文件热度、任务功耗等诸多特征。基于这些特征，可以更有针对性地对数据块作整体规划，从而使任务执行效率更高、耗时更短、节点利用率更均衡。这类方法对时效性要求不高，常采用启发式算法搜索可行方案。

基于多目标优化的副本放置策略MORM［3］将副本放置视为多目标优化问题进行处理，通过人工免疫算法，以副本放置表为个体，经过交叉、突变得出新的个体，同时以平均文件失效率、平均服务时间、节点负载方差、能量消耗、访问延迟5 项指标对这些个体进行评估及标量化处理，得到可作为适应度函数的一维向量，进而选取多个目标值都尽可能小的个体作为解决方案。该方法提供了处理这类问题一个非常好的思路，可以很好地平衡各个因素。PRPP［4］作为一种分块副本放置策略，其目的是在符合HDFS 默认的副本放置规则下，使得每个节点副本数量几乎完全一致，但由于其前提是集群节点性能以及块大小均相同（同构环境），因此适应性不佳。ISRPP［5］是SRPP［6］的改进版，两者都针对异构环境，但SRPP 假设同一机架上的节点计算性能相同，而ISRPP 考虑了各节点的计算性能，并采用数字划分的方法使得各节点分配到匹配自身计算能力的副本数。这种方法适用于分批次载入的数据集，由于其未引入高复杂度的算法，可应用于实际场景。

1.2 动态场景下的副本放置策略相关研究

此类场景类似于用户对Web 服务器的访问，需要实时对到达的写请求进行处理，因此需要动态获取节点的磁盘、CPU、内存、网络情况等信息，处理速度较快，并考虑了放置策略对之后任务执行和数据访问效果的影响。

Qu 等［7］提出基于马尔可夫链的动态副本放置模型，首先利用基于文件访问热度的马尔可夫模型调整文件副本因子，然后参考文件访问的平稳分布以及节点和机架的磁盘占用情况动态选择放置节点，实验结果证明，该方法能使数据在节点间和机架内更均匀地分布；Shithil 等［8］提出基于异构环境的动态数据管理策略，从存储情况和计算性能两方面衡量节点，通过统计学中的z 值对节点的评估值进行量化，并藉此为数据块安排位置；袁丽娜［9］对5 个指标进行考量，包括磁盘容量、CPU 负载、内存空闲率、磁盘I/O及网络带宽剩余量，通过线性加权得到综合评价指标，其系数通过变异系数法取得，改进的放置策略减少了集群任务执行时间，提升了集群的整体性能。

基于上述文献的思路和成果，本文综合考虑了副本失效率、节点负载程度以及读取能力（HDFS 的读写策略是一次写入、多次读取，因此更偏重于读取能力），因为是多目标问题，引入二进制的多目标灰狼优化算法并对其进行了改进。

2 副本放置改进策略

2.1 静态场景下默认副本放置策略的不足

HDFS 默认的副本策略在数据量大时容易出现的问题包括：数据节点负载不均、大量数据放置在处理能力弱的节点上，导致集群的任务执行速度受限、吞吐量降低。这些问题主要由以下几方面原因导致：①随机选择节点的方式没有考虑到时间和空间的局部性原理，容易导致负载严重不均，增大节点失效机率；②Dai 等［4］提出将两个节点放置在同一机架、另一节点放置在其它机架所导致的数据分布不均问题；③默认副本策略没有考虑到异构环境中各节点存储、计算、读写等性能的差异。

2.2 改进的静态副本放置策略模型

假设有m 个参数p1,p2…pm，n 个以p1,p2…pm为自变量的目标函数f1,f2…fn，k 个约束条件（等式或不等式约束）C1,C2…Ck，则多目标优化问题可表示为：

由于多个目标函数构成的向量无法直接比较，NSGAII 算法［10］规定了一种非支配排序方法：向量是第i维为1、其余为0 的单位向量；对于两个k 维向量，如果对所有的i∈1,…,k都有，而且存在至少一个i∈1,…,k，使得，则称支配，否则构成非支配关系。对于一个向量集合S，如果某个向量v→不被任何集合中的向量支配，则这样的向量构成pareto 边界。

通常认为多目标优化的最优解集是通过上述非支配排序或标量化的方式比较目标函数，最终在pareto 边界中取得的。具体优化方法一般分为两种：①启发式算法。例如NSGA-II 中采用的遗传算法、Ferreira 等［11］提出的多目标模拟退火算法等，利用了启发式算法搜索能力强、复杂度可控的特点；②结合强化学习方法［12］。强化学习［13］通过智能体（agent）做出动作并收到环境的反馈，藉此调整行动方案，从而适应环境，找到最佳策略。通过引入多目标函数，可使策略搜索和更新过程中对每个目标都有所关注，适用于解决状态空间有限的优化问题。

灰狼优化算法［14］是近年来提出的一种受生物学启发［15-17］的优化算法，原算法适用于连续的适应度函数（即目标函数）。如Emary 等［18］提出一种二进制的灰狼优化算法，将适应度函数的定义域变为离散空间。多目标灰狼优化算法［19］改善了原算法稳定性不佳、倾向于陷入局部最优的问题。崔明朗等［20］提出两条改进策略：①引入个体对周围个体的观察，更有可能跳出局部最优；②使用幂函数而非线性函数调整控制参数，使算法的搜寻过程更加稳定。

实验结果表明，多目标灰狼优化算法的结果集倾向于聚集在很小的范围内，其个体多样性差，具有易陷入局部最优的缺点。经过分析，本文得出结论：该算法的狼群位置更新主要受3 匹头狼影响，如果3 匹头狼都处在某局部最优点附近，狼群极有可能陷入该局部最优。本文认为可能导致该问题的因素之一为：Archive 集合仅包含pareto 前沿的个体，在出现优势个体的情况下，Archive 集合中的多个个体被淘汰，个体总数减少，更容易出现陷入局部最优情况。对此，本文提出改进算法以增大头狼选择范围，丰富灰狼的个体多样性，以减少算法陷入局部最优的概率。

以下介绍该方法所用到的符号及概念定义（假设集群由m 个相互独立的数据节点D1,D2…Dm组成，这些节点需要存储n 个数据块b1,b2…bn）。

（1）副本失效。无可用副本导致访问失败的几率。首先定义每个节点的失效率为fD1,fD2…fDm，然后引入副本放置表，如表1 所示，b1有3 份副本分别在D1、D2和D4。

Table 1 Placement of replicas表1 副本放置表

引入Φ(i,j)=1（表1 中第i行第j列的值）表示bi的副本在Dj上存在，否则函数值为0。bi的副本失效率为：

其中，Π*表示忽略零因子的连乘符号，假如表1 中fD2=0.005，fD4=0.001，则fb2=(1× 0.005) × (1× 0.001)=5 × 10-6。平均副本失效率定义为：

（2）磁盘相对负载标准差。假设第i个节点的已用空间为Usedi，总空间为Capi，则该节点的磁盘使用率为DUi=Usedi/Capi。集群空间使用率为：

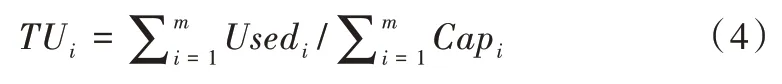
第i个节点的相对负载率为RLi=DUi/TUi，该指标大于1 的节点处于过载状态，应进行数据转移以使数据分布更加均匀。由此得到磁盘相对负载标准差为：

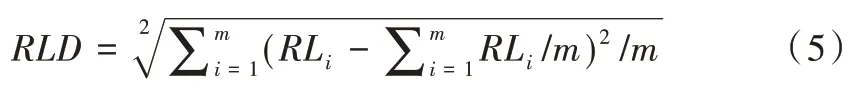
该指标反映了集群整体的数据分布均衡度。

（3）读取评价因子。假设第i个节点的磁盘读取速度为RSi，第j个数据块大小为Sj，则读取时间为：

由此得到，第j个数据块的块读取速度bRSj=Sj/RTj。

读取评价因子REF 为块读取速度倒数的均值，即：

副本放置策略必须满足以下两个约束条件：

条件1：每个数据块副本数不得小于2。

条件2：数据块副本大小之和不大于所在数据节点容量。

2.3 算法描述

2.3.1 灰狼优化算法

原始的灰狼优化算法应用于连续的解空间，且目标函数只有一个。灰狼群体被划分为4 个等级，α、β 和δ 为3 匹头狼，其余狼称为ω，它们的更新围绕着头狼进行。首先定义灰狼与猎物的距离：

2.3.2 二进制灰狼优化算法更新方式

假设有m 个节点、n 个数据块，则个体是大小为m×n 的布尔向量，存储了数据块的副本个数和存放位置。区别于原版灰狼优化算法［14］，本文方法中的个体以二进制形式保存，并按照二进制灰狼算法［18］中介绍的方式进行更新。

式中，rand是从正态分布中获取的［0，1］范围内的随机数。计算公式如下：

其中，t为当前迭代次数，Maxiter为最大迭代次数,属于区间为［0，1］的随机向量，维度与个体相同。x2和x3的计算类似于x1，仅将上述符号中的α 替换为β 和δ 即可。接下来有：

crossover 为3 个布尔向量的混合函数：

以上就是个体更新过程，更新完成后检查新个体是否符合约束条件，如不符合则重新更新，直到产生符合条件的新个体为止。

2.3.3 多目标灰狼优化算法不同点

（1）头狼选择。灰狼种群中最优的3 匹狼定义为α、β和δ，由于目标函数有3 个，不能用一般的方法为个体排序。多目标灰狼优化算法中设置了非支配种群Archive，在初始种群生成后（每个生成个体必须符合约束条件，否则需要重新生成）和每次个体更新完成后，更新Archive：

若Archive 中的个体数为0，则对种群中每个个体与其他个体进行非支配排序，如果个体不被任何其他个体支配，则将其加入Archive 中。如果Archive 中的个体超过设定上限，则执行网格策略（在后文介绍），去掉多出的个体后加入新个体。

若Archive 中已有个体，则将种群中更新后的个体与Archive 中的每个个体作非支配排序，如果：①更新后的个体被Archive 中的任意个体支配，则不能加入Archive；②更新后的个体支配Archive 中的个体集合S，则将该个体加入Archive，并踢出集合S 中的个体；③更新后的个体不被Archive 中的任意个体支配，则加入Archive。

（2）网格策略。将Archive 中的个体按同一维度i 的两个极值构成区间，将该区间等距离划分为n 组，每个个体第i 维目标函数值落在的区间号∈［0，1，…，n-1］记为个体在第i 维的网格坐标，以此得到个体的网格向量，向量相同的两个个体处于同一网格中。每当要从Archive中删除个体时，从个体数最多的网格中随机踢出个体。以上说明了Archive，即非支配种群的产生和更新，下面叙述头狼（即α、β 和δ）的选择。

采用轮盘赌的方式按顺序选择α、β 和δ，每个个体被选定的概率如下：

其中,Ni为个体所在网格的个体总数，c 是大于1 的常数。

2.3.4 改进的多目标灰狼优化算法

本文基于上述多目标灰狼算法提出以下改动：

（1）将Archive 集合分成layer1 和layer2，其中layer1 中存储最优个体，layer2 中存储次优个体。加入惩罚因子p∈（0，1），用于调节次优个体被选为头狼的概率：属于layer2的个体被选定的概率需要在原概率基础上乘以（1-p），使得次优个体在可能被选为头狼的同时，避免因其过多地影响狼群位置的更新而导致收敛速度变慢。

（2）个体加入Archive 的过程变为如下步骤：个体首先尝试加入layer1，如果成功，将layer1 中被支配个体的集合移入layer2，否则个体加入layer2。

（3）Archive 中个体数超过上限时，淘汰策略修改如下：从个体数最多的网格中踢出个体时，如果个体属于layer2，将以惩罚因子p 的概率被踢出，否则将以（1-p）/10 的概率被踢出。这样做是为了保护layer1 中的最优个体，使其被踢出的机率更小。

算法伪代码如下：

3 实验结果

3.1 实验环境与配置

实验仿真平台为CloudSim4.0，主机硬件配置如下：CPU为六核Intel（R）Xeon（R）E5-2603 1.60GHz（64G 内存，1T 硬盘）；操作系统为CentOS Linux release 7.5.1804；Java 环境为JDK1.8。

仿真集群中的节点在CPU 性能、硬盘配置、内存大小及失效率方面表现各异。节点之间较大的配置差异有助于更好地模拟异构环境，从而令默认策略与本文提出改进策略之间的差异更明显，优缺点对比更清晰。

3.2 改进多目标灰狼优化算法实验

第一组实验将原版多目标灰狼优化算法与上文提出的改进多目标灰狼优化算法作对比。实验参数包括：狼群数量为30，Archive 上限为30，迭代总次数为1 000。为评价多目标优化算法的效果，本文引入两个指标：

（1）GD（Generational Distance），用来衡量结果集中个体到Pareto 前沿的最小距离，如式（21）所示，其中Ps是Pareto 前沿，S 是优化算法的结果集。GD 主要用于评价算法收敛程度，其值越小，优化的结果越接近Pareto 前沿。

（2）IGD（Inverted Generational Distance）是对GD 作反向映射得到的指标，用于衡量Pareto 前沿到结果集的最小距离，如式（22）所示。IGD 指标对结果集的收敛程度和丰富程度进行了综合评价，IGD 越小，则算法得到的结果有更高的精度与更佳的个体多样性。

上式在实际运算中应作离散化处理，在Pareto 前沿上均匀取值，构成离散的Ps集合，然后计算式（23）。

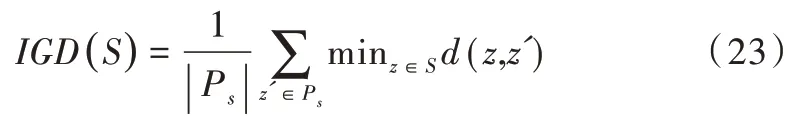
GD 指标的缺点在于无法评估结果集的多样性，也即结果集分布在Pareto 前沿附近的范围大小；IGD 指标的缺点在于其对异常值不敏感，当多个较优结果出现时即可得到较优的IGD 值。因此，本文从GD 和IGD 两方面评价多目标优化算法，以更全面地反映算法效果。本节采用DTLZ2 测试函数（有3 个目标函数）进行实验，以验证改进的多目标灰狼优化算法对于本文提出模型的适用性。DTLZ2 函数表示如下：

式中，m=12，DTLZ2 的pareto 前沿是圆心位于原点、半径为1 的球面在x、y、z 正半轴的部分。本节同样以GD 和IGD 指标衡量原始算法和改进算法在DTLZ2 上的效果，实验结果表明，当惩罚因子p=0.7 时效果较好，因此以下实验均取该值。表2、表3 分别展示了原始算法和改进算法在DTLZ2 上GD 与IGD 值的均值、最大值、最小值及方差。在GD 值方面，改进算法的均值、最大值和最小值均优于原始算法，IGD 值也同样如此。只是改进算法的方差大于原始算法，这是由于改进算法的个体多样性优于原始算法，所以在稳定性方面稍差。

Table 2 GD values of the DTLZ2 test function of original and improved algorithm表2 原始算法与改进算法在DTLZ2 上的GD 值比较

Table 3 IGD values of the DTLZ2 test function of original and improved algorithm表3 原始算法与改进算法在DTLZ2 上的IGD 值比较

3.3 静态副本放置策略改进方法实验

第二组实验是测试基于多目标灰狼优化算法的副本放置策略，应用场景是分批次的数据存储。首先使用算法计算出Archive 集合中的多个副本放置策略，算法参数如下：种群数量为50，Archive 集合上限为10，迭代次数为500次，惩罚因子p 取0.7。向集群中写入500 个数据块，大小均为64MB，每个数据块有若干个副本，放置策略符合约束条件。因此，算法中个体模型为500×11 的二进制矩阵将作为长度为5 500 的二进制序列进行处理，按照稀疏矩阵存储可大幅减少空间占用。默认与改进策略相对负载率对比如图1 所示。

Fig.1 Relative load of default and improved strategy图1 默认与改进策略相对负载率对比

由图1 可知，改进策略围绕着相对负载率为1 的直线上下浮动，而默认策略的波动非常大。从统计学的角度来看，默认策略的相对负载率极差为1.142，而改进策略只有0.169；在标准差方面，默认策略为0.349，而改进策略为0.054。以容量最大的节点2、3、7 为例，原策略的相对负载率分别为0.491、0.767、0.690，大量空间没有被利用，而改进策略为0.967、0.932、0.958。再以容量最小的节点0、1、6、8为例，在原策略下，其相对负载率为1.395、1.319、1.426、1.196，属于超载状态，而改进策略下对应值为1.092、1.058、1.023、1.040，使用情况优于默认策略。不仅整体的数据负载均衡程度更高，而且每个节点的相对负载率更接近，集群的数据块副本总数也更少。默认策略中副本因子为3，500 个数据块共生成了1 500 个副本，而改进策略中每个数据块最低有2 个副本。经统计，改进策略的副本总数为1 384 个，比默认策略更节省空间。

将算法的另外两个优化评价目标（平均副本失效率和读取评价因子）应用于数据块随机读取任务。图2 的横轴表示随机读取数据块的数量（每块64MB），纵轴为任务耗时。可以发现，随着数据块数量的增加，任务耗时的增速也有所提高，这是由于读取工作量增大后，副本访问失效次数增加，访问到读取速度较低节点的概率也增大，这两点体现了读取评价因子和平均副本失效率。当随机访问数据块数量在50～200 之间时，两种策略差别不大，但当数据块数量大于200 时，改进策略逐渐显示了其优势，在数量为200、300、400、500 时，改进策略的耗时较默认策略分别减少了31.8%、44.7%、42.2%、45.4%。当数量增大到300 以上时，改进策略的耗时几乎只有默认策略的一半。

Fig.2 Time taken to complete random read tasks图2 随机读取数据块任务完成时间比

综合以上两组实验可以看出，本文提出的改进多目标灰狼优化算法所生成的副本放置策略基本达到了使3 个目标函数（平均副本失效率、相对负载率标准差及读取评价因子）值都尽可能低的目的。

4 结语

本文针对HDFS 默认副本放置策略存在的未综合考虑节点性能，从而可能导致负载不均衡的问题，进行了以下研究工作：改进了基于二进制多目标灰狼优化算法的副本放置策略，综合考虑了副本失效率、集群整体读取性能和集群负载均衡3 项因素。实验结果显示，本文方法可行、有效，具有不易陷入局部最优、解更具多样性的特点，且负载均衡度更佳，数据块随机读取耗时更短，改善了静态场景下HDFS 默认副本放置策略未考虑节点差异、优化不充分的问题。基于当前工作，后续会开展以下几个方向的研究：①采用带权重的标量化方法代替目前的多目标策略，通过权值调节不同目标函数的重要程度；②引入更多节点性能评估指标，如能量消耗等，同时细化网络模型，以更好地反映节点之间的网络状态。