从热点概念导向信息技术教学中的计算思维培养

陈凯

人的头脑借助概念的生成、运动和反馈来进行认知，语言符号紧密地参与到认知过程中，它是人与人之间传达概念的最重要的途径。当人们提及某个概念的指称的时候——在绝大部分的交流情况下概念不得不依附于它的指称，这个指称的实际意义又与语境密切相关。所谓语境，一般就是指语言运用时的环境，如语言使用的时间、地点、场合，举例说，控制论语境中的“信息”一词的意义，与信息论中“信息”一词的含义有所不同，而以上两者又与人们日常生活中用到的“信息”这个词语在含义上有所不同。人们在获得某个概念的指称的时候，如果这个概念是熟悉的，则可以将这个指称还原为概念本身;如果这个概念是陌生的，根据建构主义的观点，则会试图将这个概念纳入自己已有的认知图示中，这个纳入过程需要同化、顺应、平衡等一系列过程，乃至重构认知图式。显然，会存在这样的情况，认知主体在获得概念指称的时候，并没有意识到，这个指称在新的情境中可能与自己所熟知的情境的意义存在很大不同，于是，仅仅简单地将这个指称还原为自身已有的认知图式的一部分，这便使得需要进行的认知建构过程并没能真正发生。

一个简单的实验就可以证明这一点，这个实验可以成为项目学习活动的一部分：假设让学生在纸上写下任意语言符号，也可以绘制图像，用来列举什么是数据，什么是计算，这里的“列举”的意思是，学生写下的这些语言符号或绘制的图像不能是直接对概念试图作解释和描绘，而只能是数据和计算的某些实例，那么，教师就可以通过观察这些实例，还原出学生头脑中对于“数据”和“计算”指称在他们头脑中还原的尽可能真实的情况。

实验结果是，有大概一半的学生在纸上写下了各种数字，其他的则五花八门，有文字符号，有图案，或者也会有其他的叙述，如动漫角色档案、武功秘籍、聊天记录、游戏存档等，这里不一一列举。在这一半写下了各种数字的例子中，有接近一半的学生为自己写下的数字进行了附加的说明，用以解释这些数字的用途，其余的，有的按规律写下数字序号，有的只是随便写了几个数字而已。

在计算一栏下，学生们列举的内容更有集中性，大约三分之二是各种不同的数学运算公式，相当多的学生就写了“1+1=2”，而其余学生，根据其列举的内容，能猜测出他们将“计算”这个词语大致等同于对“数据进行某种处理”，在这些例子中，学生往往会画一些符号，然后画上一个箭头，在箭头所指方向画上另一些符号，但箭头处究竟做了什么却是无法获知的，这样的答卷不在少数。有不到百分之十的学生，提到了对数据进行处理的规则，但只有更少的学生将规则是什么具体列举了出来。

假如给出这样的提示：你正在设计一个能在一定程度上模拟人进行计算的机器，那么你所列举的数据和计算又会是些什么？当给出这样的提示后，学生们的回答就变得相当统一，在“数据”一栏下，很多学生给出的是一些由0和1组成的符号串，在“计算”一栏下，很多学生给出的往往是几行程序代码。到目前为止，这个活动能否展现出学生的信息意识和计算思维方面的能力呢？答案是未必，原因是，学生在进行列举的时候，已经对教师的期望产生了某种预估。当教师没有给出提示的时候，“数据”和“计算”的意义并没有和信息技术学科紧密关联，当教师给出提示的时候，学生无疑联想到了课程中的概念，如二进制、算法，但这些概念只是和教师的问题产生了简单的对应关系，而不是借助概念解决了某个问题，这个过程中还是没有能体现出学生所有的意识和思维能力。为了证明这一点，只要将提示改成：你正在设计一个能在一定程度上模拟人的智能的机器，那么收回的答卷中，就会有相当多的机器人的图样了。

无论是“数据”还是“计算”，这些都是课程中出现频次很高的称谓，为了消除学生通过热点概念的简单套用来应对教师所提出问题的状况，笔者设计了一系列活动，试图让学生在信息技术或计算机科学的语境中，重构出“数据”和“计算”的意义。

● 从现实世界到数据

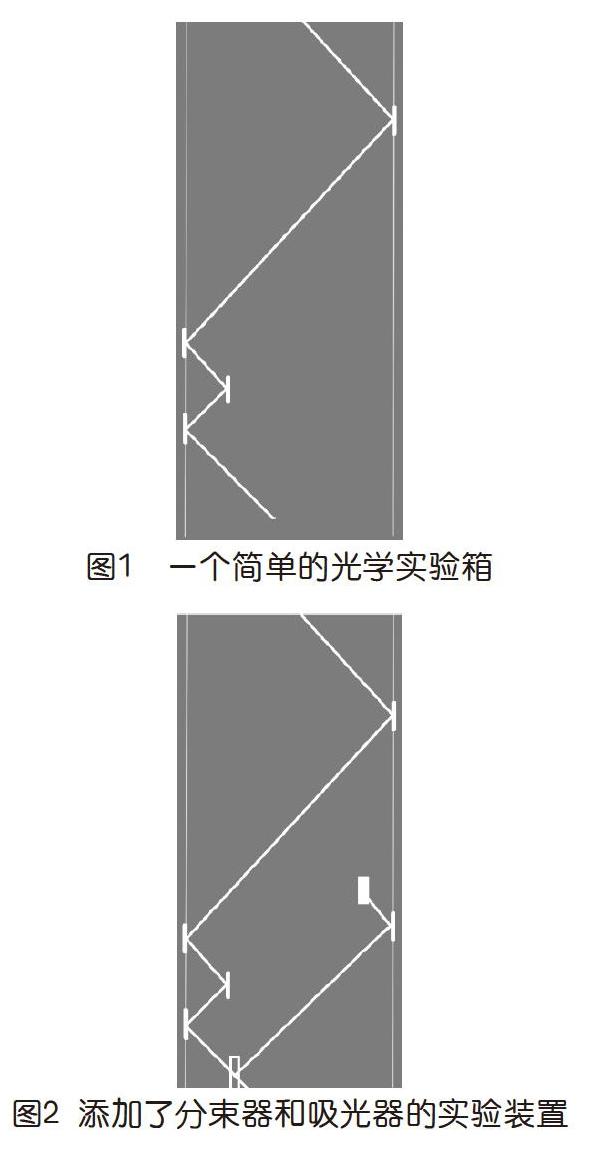
假设有这样一个物理光学实验箱，它由可发出单一光线的光源和一系列镜子组成，只要在实验箱中设置好光源和光线射出方向，并摆放镜子，就可以观察光的路径（如图1）。网络上有不少模拟光学实验的模拟器，不过这些模拟器大多只能进行比较简单的反射或透射的模拟，缺少像分束器、偏振光片这样的设备。所以可以考虑一下，自己怎么制作一个功能更丰富的虚拟的光学实验箱？乍看上去，好像是件挺困难的事，但若实验中所有光源射出的光线都和水平方向呈45度角射出，那么實现光束和器件之间的模拟，就变得很容易。

考虑有一个表格，表格中有这样一些数据，其中H代表镜子（当然，用其他任何字母都可以），L代表向左前方45度角射出的光线，R代表向右前方45度角射出的光线，那么就可以将现实中的光学实验箱变成数据，如表1所示。

接下来要做的是，按规则来填写表格。规则如下：如果L的左前方是空的，则在左前方补充L;如果R的右前方是空的，则在右前方补充R;如果L的左前方是H，则越过一行，在更前方的格子里补充R;如果R的右前方是H，则越过一行，在更前方的格子补充L。如果一直按这个规则填写表格，表格中数据则变成如下页表2所示的模样。在这个时候，重新审视什么是“数据”就显得很有意义了，教师可以明示的是，虽然毫无疑问这些数据记录了光线行进的路径，并且，数据的记录也正是自然科学研究中常做的事，但在上述例子中，重点并不是记录，而是仿真。一系列符号通过简单的规则仿真了光和器件之间的交互的行为，尽管在这个例子中，仿真仅仅限定在45度角射出光后的状况，也没有涉及光的强度、频率等更多特征，但实验足够能展现出这些数据按规则进行的变化，是具有仿真各种现象的潜力的。

这个例子也呈现出计算机科学中“计算”一词的特性，那就是严格根据规则来进行符号的变化，并且，这些规则对所有的数据都是齐一的。“齐一性”是个哲学术语，它指的是在自然界中如果事件的因是相同的，那么，在相同的情形下后续事件不仅将再发生而且会一直发生，由因致果的进程是齐一的。“计算”这个名词在计算机科学里有着特定的意义，它与图灵机的运行方式有着密切的关系，但对普遍的教学而言，若在“数据与计算”的模块中引入图灵机的概念，不仅提升了概念理解上的难度，而且会引出更多难解的新问题。笔者设计此项填图游戏的目的，是让学生理解“数据与计算”的“计算”一词与日常语境中的“计算”一词在意义上是有很大区别的：数据不仅仅是某个计算任务的对象，也实际参与到了计算模型的构造过程中，它的存在形式和变化行为是被严格规定的。

● 现实与虚拟现实的对应

接下来，就可以用很简单的方法，为这个虚拟的光学实验箱添加各种各样的有趣设备了。如分束器，这个设备可以将光线一分为二;还有吸光器，它能阻止光线的继续传播。在现实世界中，的确存在这样的实验设备。这些设备的行为方式如上页图2所示，其中空心矩形代表分束器，实心矩形代表吸光器。

定义分束器的规则也很简单，如在表格中用S代表分束器，用O代表吸光器。当某个L的左前方是分束器的时候，则在左前方格子的更左前方格子中补充L，同时在正前方格子的更正前方格子中补充R，如表3所示。

吸光器的行为自然而然就能达成，根本不需要为其定义规则。当没有可匹配规则的时候，填图工作自然就停止了，如表4所示。

在模拟实验中，可以构造出一些现实中可能不存在（至少淘宝网店是没有供应的）的设备器件，如用符号C来代表“光算器”（虽然是杜撰的名词，但其实与某种逻辑运算过程有所对应），假设有两种偏振方向不同的光源，一种用大写字母表示，如L或R，一种用小写字母表示，如r或l，当“光算器”C同时接收到两种光线的时候，它会过滤掉其中一种而通过另一种光线，过滤规则如下——规则1：r和l则通过R;规则2：r和L则通过R;规则3：R和l则通过R;规则4：R和L则通过r。

只要学过简单的数字逻辑，那么就可以知道，上述规则实际上对应与非门的行为，但学生也未必一定需要记得这个名词，他们只要能够对应规则，正确地预测出这个虚拟光学试验箱的行为就可以了，并且，大家也较能认可这个装置在现实中是能够被制作出来的。接下来，通过在实验箱里，在恰当的位置摆放光源、镜子、分光器和两个“光算器”，就可以让这个光学实验箱进行乘法运算了。这里，将这个乘法装置命名为M，最初始输入的数据分别放置在底部最左和最右处，输出放置在装置顶部最右处，之所以要对乘法装置另外命名，并且还要规定输入和输出的位置，是有其他道理的，后文中还会提到。装置中器件的安置和光线路径变化如表5所示。

如果将输入区和输出区的大写字母看作数字1，小写字母看作数字0，则可发现，此装置能正确地计算出两个一位二进制数码的乘法运算的结果。

到目前为止，虚拟的光学实验箱和真实的光学实验箱存在对应关系，但仔细想想，这种对应不是必然的，尤其是对于计算这种行为而言，装置的构造是可以脱离物理现实的。

● 从现实需求到思维过程的真实

假设有这样一个听上去很现实的需求：某个提案需要五位代表一致同意才能通过，根据投票的状况，怎么用一个光学实验箱计算出提案是否通过？从数学上看，只要设赞同票为1，设否决票为0，然后对各票进行乘法运算即可。但正如前文所说，计算机学科语境中的“计算”，是要按规则对输入符号进行一系列转换后得出结果，而不是用数学乘法运算求得结果。一个真实的光学实验箱也能完成这个任务，但为了运算五个数字的乘法，这个实验箱中需要四套乘法装置，装置规模一下子就变大了。

对于虚拟的光学实验箱而言，解决办法可以是这样的：首先设计一个专门用于进行乘法运算的虚拟实验箱，左下角和右下角为输入，而实验箱的右上角是输出，并将其定义为符号M，而M的具体结构和行为前文中已有说明了。那么，为了计算五个一位二进制数字的乘法，只要在特定位置放置四个M，就能轻松完成装置的设计任务了。这其中就体现出模块化和封装的思想的重要性。同样，也可以借助更多的“光算器”等设备设计并定义出其他装置，如专门做加法的装置。一个一位二进制加法装置需要两个输入数据和两个输出数据，至少要用到五个“光算器”。

对五个一位二进制数字进行乘法运算的过程如表6所示，显然，只要有一个输入是小写字母，结果就必然是小写字母。

在现实中，要做到同样的事情是很困难的，因为不可能将装置的空间进行压缩，此外，复制一模一样的M装置也是耗时耗力的工作，但在虚拟的世界中，只需定义好一套M装置，并规定好输入和输出的位置，就可以无数次地重复去使用它，并且它可以被随意复制粘贴到装置的任意处发挥作用。

想象一下，如果这个虚拟光学实验箱不是通过手工填图来完成的，而是能自动填图的设备，那么应该如何将它制造出来？最容易想到的，是设计一个并行的扫描和匹配装置，众多传感器组密布于表格上方，每个传感器组只负责3×3范围的区域，按匹配规则对空白区域进行填空。为了使这个装置能正常工作，还需要引入一个加速器T，其作用是对数据的变化速度进行同步，之所以需要加速器，是因为这个虚拟光学实验箱是借助二维的表格来存储数据的，每个格子中只能存放一个符号，因此每次进行某种运算的时候，因为代表数据的符号和代表计算设备的符号（这个符号同样以数据的形式存在）无法共存于一个格子中，所以计算结果会以“超时空”的方式出现在运算符号右上角，但这样就会使得其他数据的变化速度与之不同步，因此才有必要使用到加速器，使用示例如表7所示。

可以看出，加速器是纯粹为了计算得以顺利进行而引入的一种数据，它在这个装置中存在的理由是自洽的，并不需要专门为其寻找一个现实世界中的原型。

当使用数据和计算协同构建起一个计算装置的时候，尽管这个装置是虚拟的数码物，但它不仅能够完成，而且能更高效地完成现实生活中的计算任务。所以说，当为教学活动设定一个情境或任务的时候，教学情境的真实性可能并不仅仅对应现实物理事件的真实性，也对应一个由思维过程生發并主要以数据形式存在的虚拟数码物。当谈及计算思维时，常能见到的有这样一段说明文字：计算思维是运用计算机科学的基础概念进行问题求解、系统设计以及人类行为理解等涵盖计算机科学之广度的一系列思维活动。但周以真说，计算思维是人的思维，不是计算机的思维。这两段文字可能会让初学者难以理解、无所适从。但本文的例子给出了一个解释的途径，当一个人在虚拟的光学实验箱内，严格按规则进行填图的时候，他就是在按计算机的思维进行工作，类似的，某人或许能娴熟使用分支结构语句和循环语句解决诸如枚举、查找等问题，然而他或许只是按一个更庞大、更复杂的规则系统来解答问题，其中体现的仍然只是计算机的思维而已。那么，怎样的思维才是计算思维呢？笔者认为，从数据和计算的角度看，计算思维的重点不在于用数据和计算直接解决某实际问题，而是要用数据和计算构筑起一个可以自动计算的模型来解决问题，既然是模型，那么它既可以是实物，也可以是虚拟的数码物，或者，以两者相互整合的方式，融入到生活的方方面面。