大观念统领下单元学习任务的开发
刘延革 冯林
摘要围绕大观念进行单元教学设计,可以提升教师教学设计站位,促进学生核心素养的形成。以小学数学“图形与几何”领域中“图形认识”板块的教学为例,梳理大观念统领下开发学习任务的基本逻辑,具体阐述构建单元学习任务的流程。包括根据大观念确定单元具体观念,制定预期目标,形成关键问题或子问题,确定系列单元学习任务;把握活动目标、活动情境、核心问题、学习材料等要素,设计具体可操作的学习任务。此外还要在课堂教学中保证学生高水平的认知参与,由此促进学生对重要知识和思想方法的理解和迁移。
关键词 大观念;单元具体观念;学习任务;关键问题;活动情境
中图分类号G63
文献标识码B
文章编号1002-2384(2021)05-0032-04
在核心素养视域下,单元成为教师进行教学研究的基本单位。[1]围绕“大观念”进行单元教学设计,能让教师从课时教学中跳出来,提升教学设计的站位;能够为学生获取新知提供组织架构,为将来更高层次的学习提供理解基础。[2]那么,如何在大观念指引下设计有效的学习任务,并通过学习任务的实施形成对大观念的研究,就显得尤为重要。本文仅以小学数学“图形与几何”领域中“图形认识”板块的教学为例,具体阐述如何在大观念统领下进行单元学习任务的开发。
一、明确大观念的基本含义
大观念(Big Idea)也称“大概念”,当前学界对于大观念的各种表述均体现了“指向学科本质”“彰显学科价值”“概括学科结构”“提供思维模型”“具有广泛迁移性”等特征。[3]具体而言,学科大观念并非指学科中某一具体的概念或定理、法则等,而是“指向这些具体知识背后的更为本质、更为核心的概念或思想”。[4]
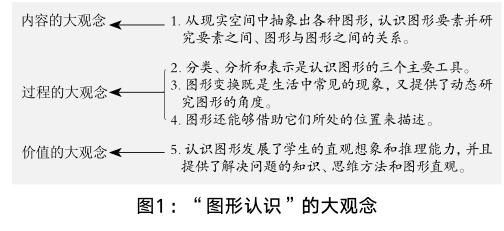
具体到数学学科,数学大观念作为数学素养和数学知识的桥梁,是内容、过程和价值的融合。[5]以“图形认识”的五条大观念为例(见图1),它们在内容、过程及价值三个维度系统回答了“学什么、怎么学、为什么学”。其中大观念1表明“学什么”,属于内容大观念;大观念2、3、4涉及“怎么学”,属于过程大观念;大观念5关乎“为什么学”,属于价值大观念。
这五条大观念要从教师的教学设计转化为学生的实际所得,需要开发一系列能激发学生深度思考的学习任务。
二、建构完整的单元教学设计体系
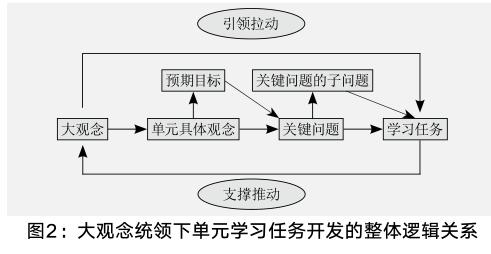
大观念是单元学习任务开发的基石,对学习任务设计起着引领拉动的作用,反过来,学习任务的实施又支撑推动着大观念的形成与完善(见图2)。从大观念出发,到确立“单元具体观念”以及相应的“预期目标”,再到确立单元“关键问题”以及分解出若干子问题等多个环节,最终形成以关键问题或子问题为驱动的具体学习任务系列,这是一个层层推进的过程,在逻辑上紧密联系,构成一个完善的单元教学设计体系。
1. 单元具体观念:实现对单元教学的引领
单元具体观念,是大观念在单元教学内容中的具体表现,是单元教学的核心内容、教学过程中形成的思想方法以及教育价值的集中体现,能够实现对单元教学的引领作用。它不仅与大观念在三个维度上有对应,而且单元与单元之间针对大观念的形成,也体现了学习进阶与迁移应用。例如:“图形认识”中《认识图形(一)》《长方体和正方体》《圆柱与圆锥》三个认识立体图形单元的单元具体观念,无论从学习内容还是学习方法上,都体现了“图形认识”大观念的学习进阶。
2. 預期目标:单元具体观念的外在表现
预期目标指向学生的学习结果,是单元具体观念的外在表现。借助这些外在表现,一方面学生头脑中所形成的单元具体观念变得可视,易于教师在单元教学过程中对学生情况的把握。另一方面,在学生经历了单元学习之后,评价学生是否形成了单元具体观念,或者评价学生对单元具体观念的理解和感悟达到了何种程度时,预期目标又可以作为重要的标准和依据。因此,确立单元具体观念的同时即要确定预期目标,二者共同作为提出关键问题的依据。
整体把握下的预期目标,一般以不同的行为动词进行层级划分,可大致分为四个层级:知道(know)、做到(do)、意识到(being)[6]和迁移到(transfer),其中知道(know)和做到(do)面向基础知识和基本技能,“意识到”更侧重情感态度和价值观层面,而“迁移到”体现了大观念的核心,能支撑学生后续相关内容的学习。学生在四个层级上的预期目标,应该是在大观念及单元具体观念的统领下逐步深入的。
需要说明的是,预期目标可以是结果性的,即学生经历学习任务之后具有的;也可以是过程性的,即学生在学习任务探究活动过程中表现出来的。
3. 关键问题:引领学生指向单元具体观念的深度思考
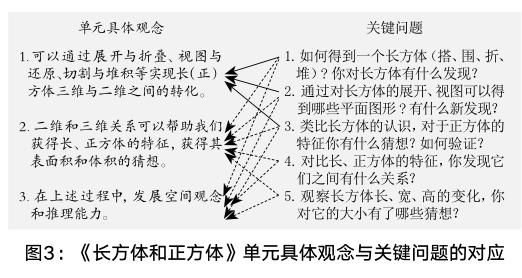
关键问题是指向单元具体观念的。确立关键问题,可以引导学生开展深度思考和合作交流,是“达到理解意义和自主迁移目标的关键”。[7]以《长方体和正方体》单元为例,单元具体观念是认识图形要素和研究图形要素之间的关系,那么关键问题就要指向这些方面(见图3)。如关键问题1“如何得到一个长方体”,直指单元具体观念1,甚至可以说是指向整个立体图形认识的,因为二维平面与三维立体之间的转化是认识立体图形的必由之路。同时从图中还可以看出,深度思考、理解并感悟关键问题的结果通常指向前两则单元具体观念,但过程则指向单元具体观念3,是意义和价值层面的对应。此外,在不同单元的关键问题之间,也要体现学生思维上的进阶。
4. 学习任务:在关键问题或子问题引领下开发
学习任务的设计会影响学生学习的质量,它不仅决定学生学习了什么,还决定他们怎么思考、发展、理解和运用数学。数学的学习任务是将学生的注意力集中在某一与数学内容相关的一系列问题或一个复杂问题上的数学活动。[8]因此,由单元具体观念衍生出的关键问题是学习任务的核心,是学生理解、感悟并形成单元具体观念的依托。
在关键问题的引领下,单元学习任务的开发有了抓手。那么,具体应该如何操作呢?
首先,以关键问题直接开发学习任务。例如:在《圆柱与圆锥》单元中,涉及3个关键问题:“是怎样得到圆柱的?所用图形与圆柱之间有怎样的关系?”“类比制作圆柱的过程,你想怎样制作圆锥部分?遇到了什么困难?是怎样解决的?”“你对圆柱、圆锥以及它们之间的关系有哪些猜想?你是怎样想到的?准备如何验证?”根据上述3个关键问题,可以分别设计“制作圆柱”“制作圆锥”“猜想圆柱和圆锥的关系”3个学习任务,呈现了关键问题与学习任务的一一对应。
其次,以关键问题分解的子问题开发学习任务。当关键问题过大时,需要将关键问题分解成几个子问题,并以子问题为核心设计系列学习任务,由此达成对关键问题的深入理解。例如:《长方体和正方体》单元的关键问题“如何得到一个长方体”,需要让学生经历搭、围、折、堆等多种操作活动,每一种操作就是以相应的子问题为核心确定了一个学习任务。如针对子问题“什么样的图形可以折成长方体”,可以设计“观察这些连在一起的长方形,想一想哪个能折成长方体”的学习任务。
三、设计具体可操作的学习任务
在单元系列任务确定之后,就可以进入一个完整的学习任务设计中。有研究表明,使用一系列情境化的高水平任务,能够促进学生在课堂上的交流,帮助学生更深入地进行数学理解。高水平学习任务的基本特征是:情境性、探究性、表征性。[9]依据此特征,本研究构建了学习任务应有的要素,包括活动目标、活动情境、核心问题、学习材料、学习单、活动形式和活动时间等。下面以“搭长方体”的学习任务为例进行各要素说明(见图4)。
1. 活动目标:体现内容、过程、价值大观念的融合
活动目标阐述了学生进行该学习任务探究后的结果预期,它与单元具体观念中的内容大观念、过程大观念与价值大观念相呼应。
根据《长方体和正方体》的单元具体观念,“搭长方体”的活动目标设定为:在搭建长方体框架的过程中,认识长方体各要素的特征(棱与顶点)以及要素之间的关系,发展推理能力。其中,内容大观念在这个活动目标中体现为认识要素及要素之间的关系,指向核心知识;过程大观念则体现在动手做长方体,指向“表示”;而价值大观念是发展学生的推理能力。这样的表述,实现了核心内容、过程方法以及教育价值的统一。

2. 活动情境:提供问题解决和意义建构的机会
活动情境是高水平任务的特征之一,真实的、有趣的、与实际生活相联系的情境能使学生把数学和生活联系起来,促进数学任务的完成。当然,这里的情境也可以是纯数学情境。无论情境的类型如何,最终都是为学生提供推理、意义建构和问题解决的机会。[10]
在“搭长方体”的学习任务中,教师给出了一组生活中的长方体实物图,有纸箱、铁丝围的框架、组装的凳子、叠放的书。情境图的出现,首先让学生感受到生活中长方体的物品很多,激发了学生的兴趣。然后在观察这些长方体时,又让学生感受到长方体可以用面围、用小棒搭,也可以由面堆积起来,让后续围、搭、堆长方体的活动有了实际出处。
3. 核心问题:指引学生深度思考的方向
在活动情境的基础上,设计能激发学生深度思考的核心问题是重中之重,因为它关乎学习任务的认知水平,直接影响学生在执行任务过程中的思维含量,指引活动的思考方向。核心问题由关键问题或者关键问题的子问题衍生而来,是关键问题或其子问题内嵌于情境中的另一种表达。形象地说,核心问题就像是给关键问题或子问题穿上了情境的外衣。
如制作长方体包括选材料和做长方体两个过程,因此涉及两个关键问题:“如何得到一个长方体?”指向做长方体之前的思考;“在做的过程中,你对长方体有什么发现?”指向做成长方体之后的反思。两个关键问题的核心引领学生关注长方体的要素及要素间的关系。在有了“搭”长方体的情境后,核心问题锁住了关键问题的“魂”;套上了搭长方体情境的外衣后,摇身一变成了“选择哪些小棒就能搭成长方体?”“在搭长方体的过程中,你有什么新发现?”等问题。正是这些把学生思维引向要素之间关系的问題,支持了学生在活动过程中的思考,促进学生的深入学习。
4. 学习材料:为学生提供执行任务的脚手架
学习材料是提供给学生的学具或学习单,旨在让学生的动手操作有物可用,思维过程有输出的载体。在“搭长方体”学习任务中,在材料支持方面,提供了长度不同的小棒和连接器,学生根据头脑中长方体的表象进行自主选择,为自主探究提供了保障。学习单作为学生执行任务的脚手架,包含活动要求、活动记录单以及活动时间的提示。
其中,活动要求是给学生的活动过程提示,明确指出每一步的所做与所想,提示学生边操作边思考。比如:在选择搭长方体材料的活动要求里,提示学生“选择哪些小棒就可以搭成长方体”,有助于学生对长方体要素之间关系的关注,能够避免学生动手操作的盲目性,让活动的认知努力高于操作努力。在此基础上,记录单上的空白部分成了学生思考结果的呈现载体,直接为后续课堂的深入交流提供了有形的支架。在学习单上,也明确提示了学生执行该活动的时间,保证学生活动有充分的时间,也能促使学生形成珍惜时间执行任务的意识。
此外,需要说明的是,每个学习任务完成的过程都应包括独立思考、小组合作、集体汇报三种形式,务必保证学生有充分的独立思考时间,为小组合作和集体交流的有效性奠定基础。活动时间的长短要依据任务的复杂程度或者所需的思维水平而定,可长可短,需要经过课堂实践检验。
大观念统领下的学习任务开发,力图促进学生对重要知识和思想方法的理解和迁移。若要实现这一目标,还需要在课堂教学中保证学生高水平的认知参与。美国“QUASAR”计划的研究结果表明,数学任务认知水平在不同的阶段会发生改变。大多数教师能够成功地设计高水平的数学任务,但是在高水平任务进入课堂环境的时候,只有三分之一的高水平任务能随着学生的实际参与保持原状。 [11]也就是说,有大量的高水平任务在实际课堂上被降低了思维含量。这启发我们,在单元学习任务的课堂实践中,一定要清楚高认知水平教学任务的影响因素,如课堂氛围、教师的教法、学生的态度等。只有针对性且有效地实施高认知水平的教学任务,才能真正落实大观念统领下单元学习任务促进学生核心素养形成的初衷。
参考文献:
[1][3][5][7] 张丹,于国文.“观念统领”的单元教学:促进学生的理解与迁移[J].课程·教材·教法,2020(5):112-118.
[2] 杨文源,刘恩山.为了理解的教学设计:从指向核心概念的问题开始[J].生物学通报,2014 (1):28-33.
[4] 顿继安,何彩霞.大概念统摄下的单元教学设计[J].基础教育课程,2019(18):6-11.
[6] Drake S M,Burns R C.Meeting Standards through Integrated Curriculum[M]. Alexandria,Virginia USA:Association for Supervision and Curriculum Development,2004:31.
[8] Stein M K Grover B W,Henningsen M. Building student capacity for mathematical thinking and reasoning:An analysis of mathematical tasks used in reform classrooms [J].American Educational Research Journal,1996(2):455–488.
[9] 胡典顺,余晓娟,王学萌,等.美国课堂高认知水平数学任务的设计与思考[J].数学教育学报,2019(6):37–41.
[10] 吴穎康.如何贯彻落实数学课程标准—美国《行动原则:确保所有学生的数学成功》评介[J].数学教育学报,2018 (2):16–23.
[11] Stein M K,等.实施初中数学课程标准的教学案例[M].李忠如,译.上海:上海教育出版社,2001:18.
(编辑 谢 凡)
注释:
① 本文系北京市教育科学“十三五”规划2020年度一般课题“运用大观念发展儿童数学关键能力的实践探索” (课题编号:CDDB2020140)的研究成果。

