基于SRAM的通用存算一体架构平台在物联网中的应用

曾剑敏 张 章* 虞志益 解光军

①(合肥工业大学电子科学与应用物理学院 合肥 230601)

②(中山大学微电子科学与技术学院 珠海 519082)

1 引言

随着移动互联网、云计算、物联网和人工智能等技术的快速发展，我们正全面步入大数据时代。大数据最重要的特征之一，也是大数据时代社会所面临最大的一个挑战：有海量的数据需要处理[1]。因为在大数据时代，包括社交媒体、生物医疗、气象、交通和航空航天等在内的多种领域均会产生海量的数据。例如当前国际射电天文界最重要的大型望远镜项目之一——平方千米阵(Square Kilometer Array， SKA)[2]，每年可以产生300 PB容量的数据[3]；一架波音喷气式客机飞行一小时就能产生约21 TB容量的数据[4]。社会所产生的数据是呈指数式爆炸增长的[5]，据全球知名数据公司IDC (International Data Corporation)发布的《数据时代2025》白皮书报告显示，到2025年，全球每年产生的数据将从2018年的33 ZB增长到175 ZB，相当于全球每天产生491 EB的数据[6]。

大数据的出现与繁荣发展使得数据处理的重心逐渐从以计算为中心转移到以数据为中心[7]，即数据处理任务或应用从计算密集型转移为数据密集型。而由于存储墙[8]和带宽墙[9]等原因，当前采用冯诺依曼架构设计的计算机系统在数据密集型计算中表现出的性能瓶颈和低能效等缺点日益凸显。因此，为了解决这些问题，新的计算机架构，特别是超越冯诺依曼(beyond von Neumann)架构，亟待提出。

近年来，存算一体(In-Memory Computing，IMC)架构引起了研究人员的广泛关注，并被认为是一种有望成为突破冯诺依曼瓶颈的新计算机架构范式。存算一体的核心思想是使得计算单元和存储单元尽量靠近，甚至融合为一体[10]。近期前沿文献中实现IMC架构的方式有多种，例如基于新兴的3D堆叠封装[11—13]或者忆阻器等非易失存储器件[14—16]来实现。然而，由于3D堆叠以及非易失存储等新兴技术并不十分成熟，基于这些技术设计的IMC架构短时间很难得到广泛应用。因此，许多文献[17—24]逐渐基于技术成熟的SRAM来探索和设计IMC架构，并证明基于SRAM的IMC架构在实现数据密集型应用时能够带来显著的性能和能效提升。例如，文献[20]为本文作者所设计的一种基于SRAM实现的通用IMC架构平台——DM-IMCA。为弥补现有文献中几乎所有基于SRAM来实现的IMC架构均面向如神经网络等专用目的而设计的缺憾，DM-IMCA能够在其内部SRAM中进行大部分的逻辑运算和算术运算，因此具有广泛的通用性，并且具有较高的潜力和价值。

为了充分挖掘DM-IMCA的应用潜力和价值，本文探索了该平台在物联网领域中的应用。详细来说，本文选取了包括物联网中信息安全、深度神经网络以及图像处理在内的若干轻量型数据密集型应用，对相关算法进行分析或者拆分，并把算法的关键部分映射到DM-IMCA的SRAM中进行计算，以达到加速应用计算或者降低功耗的目的。

2 基于SRAM的存内逻辑计算原理

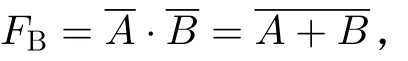
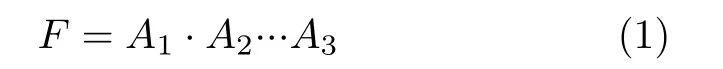
和

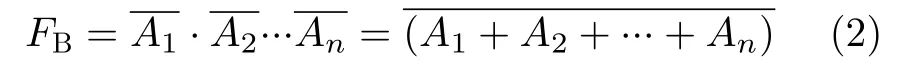
即可以利用SRAM位线的“线与”特性来实现多输入与门和或非门。

3 DM-IMCA：基于SRAM的通用IMC架构平台

3.1 DM-IMCA简介

DM-IMCA[20]是一个基于SRAM的通用IMC架构平台，其硬件架构如图2所示。DM-IMCA主要由1个6级流水精简指令集处理器核、1个指令存储器、1个存内计算协处理器——IMC-CP，以及由若干SRAM模块组成的数据存储器组成。其中处理器核是基于一款开源、具有经典5级流水且兼容MIPS32架构的低功耗轻量处理器核OpenMIPS进行裁剪与改进而来的。

图1 SRAM列内逻辑运算示意图

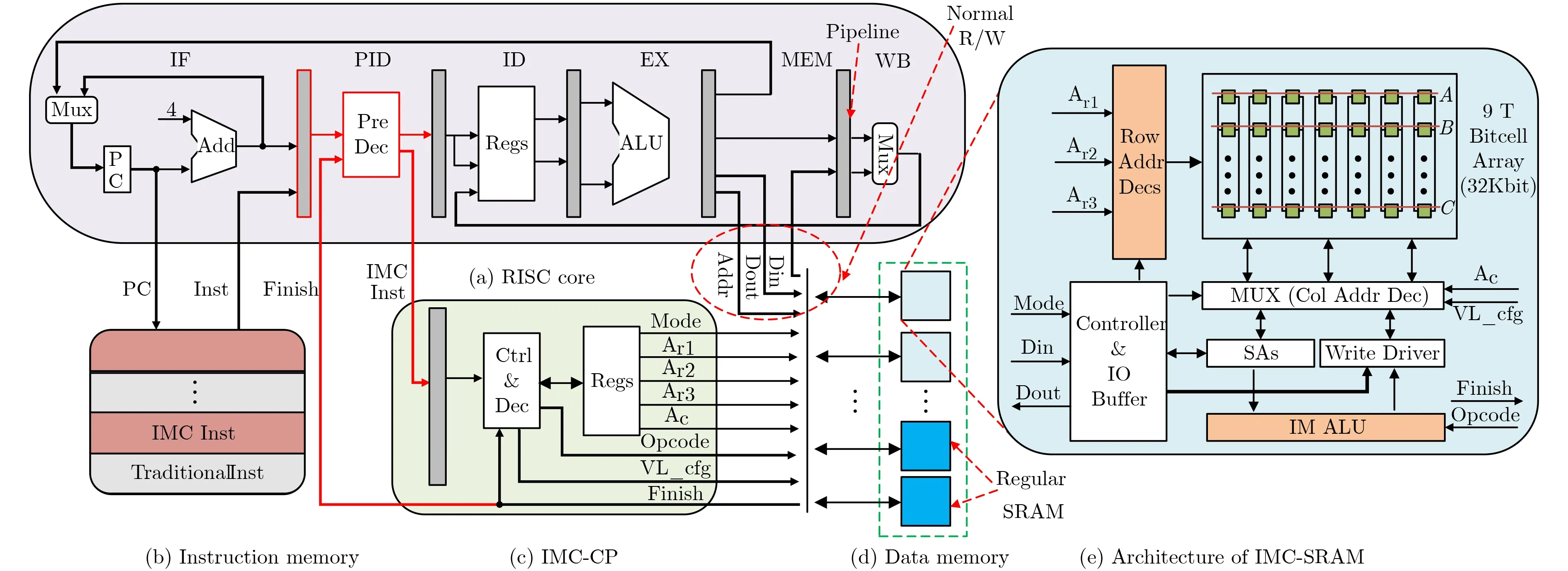
图2 DM-IMCA硬件架构图

数据存储器由若干常规SRAM模块与计算型SRAM——IMC-SRAM组成。IMC-SRAM是一款融合存储和计算为一体的SRAM，其硬件架构如图2(e)所示。IMC-SRAM是在如图1所示的电路原理基础之上，将传统6管单元换成9管单元，以消除6管单元所带来的读写互扰以及进行存内计算时的问题。此外，IMC-SRAM中还额外加入了少许逻辑门，用于实现除“与”和“或非”逻辑之外的其他运算。与已有文献相比，IMC-SRAM可以支持更多类型的运算，例如加法、移位运算等。此外，IMC-SRAM支持存内向量计算。如图2(e)所示，将向量操作数A和B沿字线方向对齐存储，那么只需1次操作，便可对存储阵列中某一行的A和B分量计算完，然后将计算结果回写至同样与A和B对齐存储的向量C中。在IMC-SRAM进行存内计算时，数据存储器中的常规SRAM仍然可以进行数据的读写操作。

IMC-CP是一个为存内计算设计的轻量协处理器，主要作用是对处理器核传送过来的IMC指令进行译码，然后根据译码后的信息对IMC-SRAM进行模式配置及控制存内计算操作，包括计算并配置操作数地址以及管理IMC-SRAM中的存内计算过程。IMC-CP中还包括几个重要的可配置的状态寄存器：

(1)R0：用来保存下一次存内计算的矢量长度信息；

(2)R1-R3：用来保存IMC-CP对IMC指令译码后得到的源操作数和目的操作数的列地址；

(3)Rm：用来保存系统当前工作模式；

(4)Rn：用来保存系统中用以存内计算的IMCSRAM模块的数量信息；

(5)Rv：保存当前IMC计算指令中的剩余矢量长度信息；

(6)Roc：保存存内计算的操作码信息。

在DM-IMCA中，运行着两套指令：传统MIPS32指令和IMC指令(IMC instruction)。前者通过完整的处理器核流水线来执行，后者在处理器核的指令预译码流水级之后，传送至IMC-CP进行二级译码，再由IMC-SRAM进行执行。两套指令长度一致，因此，并不需要设计两组不同的指令存储器，可以将传统MIPS32指令和IMC指令混合存储于同一个指令存储器中。这样做的好处是便于对系统进行程序设计，达到真正的传统指令和IMC指令混合编程的目的。对于两种指令的识别，将会交由处理器核的指令预译码流水级来进行处理。指令存储器采用常规的SRAM(通过工艺厂商提供的存储编译工具Memory Compiler生成)来进行设计。

DM-IMCA支持双工作模式：普通模式和IMC模式。当DM-IMCA工作于普通模式时，数据的运算由处理器核的流水线来完成，此时IMCSRAM与传统SRAM一样，其功能是进行数据的存取，此时DM-IMCA表现得与传统冯诺依曼架构一样；当DM-IMCA工作于IMC模式时，IMCSRAM可以进行存内计算，数据无需传送至流水线进行处理，此时DM-IMCA表现出与传统冯诺依曼架构不一样的特性。因此，DM-IMCA是一种超越传统冯诺依曼的混合架构。

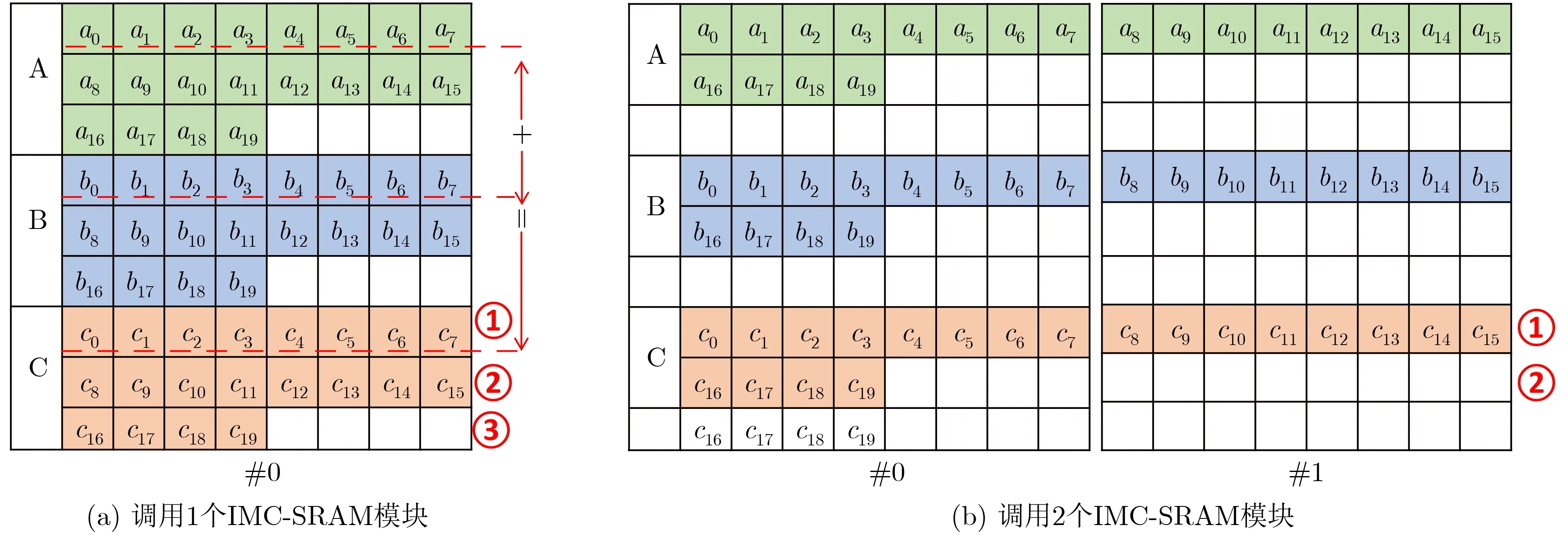
图3 存内向量计算自动化及自适应示意图

3.2 IMC指令集

DM-IMCA包含一个专门为存内计算设计的指令集——IMC指令集。DM-IMCA中的处理器核经过改进，将其中不需要的部分指令去除，将腾出的指令空间用于IMC指令的编码。IMC指令的高5位为识别码，其中前3位(110)为1级识别码，用于区分IMC指令和传统MIPS32指令。1级识别码在DMIMCA处理器核流水线中的预译码级被处理，并不会被传送至协处理器IMC-CP中。因此，处理器核传送给IMC-CP的指令实际上只有29位(IMC指令的低29位)。识别码中的后两位为2级识别码，用于分区某条IMC指令的类型。各类指令的指令格式也分别在表1中列出。

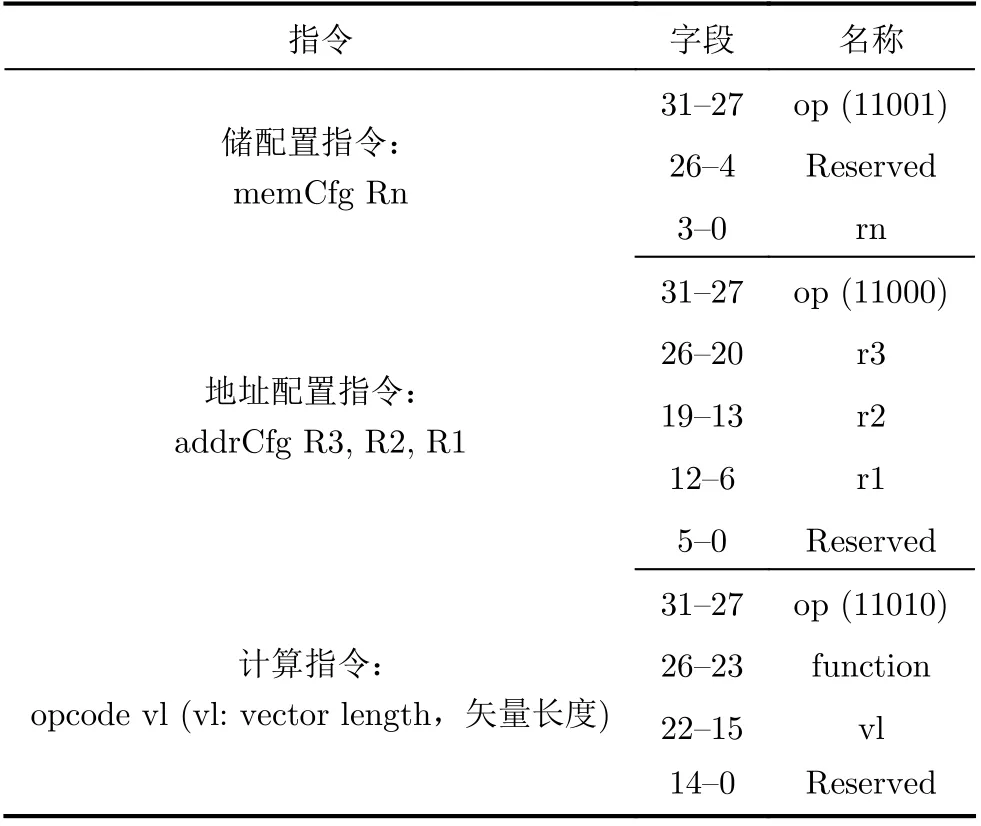
表1 IMC指令集编码格式

按照功能划分，IMC指令可以分为两大类：配置指令和计算指令，如表2所示。其中配置指令又可以分为存储配置指令和地址配置指令。存储配置指令的作用是对数据储存器中用于存内计算的IMC-SRAM宏模块数量进行配置。具体配置过程是将指令中rn字段所包含的信息写入IMC-CP中的寄存器Rn中。地址配置指令用于配置存内计算的源操作数和目的操作数的行地址信息。地址配置指令中的r1和r2字段所包含的内容为存内计算源操作数的行地址信息，r3字段所包含的内容为存内计算目的操作数的行地址信息。地址配置指令的配置过程为分别将r1字段和r2字段内容写入IMC-CP的寄存器R1和R2中，将r3字段内容写入IMC-CP的寄存器R3中。计算指令的作用是控制IMC-SRAM的存内计算，包括存内计算的功能类型和向量长度。计算指令中的function字段包含了存内计算的操作码(功能码)，用于IMC-SRAM选择特定的存内计算功能，vl字段包含了相应存内计算操作的向量长度信息。

表2 IMC指令集

3.3 DM-IMCA的工作流程

首先，在进行存内计算操作之前(一般为系统启动或者复位后)，需要执行一条存储配置指令memCfg来对IMC-CP中的寄存器Rm进行配置，以确定数据存储器中参与存内计算的IMC-SRAM宏模块数量。由于Rm在系统启动或者复位后被置为1，因此如果不对寄存器Rm进行配置，而又需要多个IMC-SRAM模块参与存内计算，存内计算将无法正确进行。

完成一个存内计算操作需要DM-IMCA连续执行两条IMC指令。第1条为地址配置指令addrCfg，第2条则是一条计算指令。第1条指令执行所包含的内容为第2条指令将执行的存内计算操作的源操作数和目的操作数的行地址信息。第1条指令被IMCCP执行完后，IMC-CP中的寄存器R1-R3将会被写入相应的操作数行地址信息，并且寄存器Rm被写入“1”，表示IMC-CP被切换到IMC模式。在随后的一个周期内，IMC-SRAM的行地址信息和工作模式将会被IMC-CP进行配置。第2条计算指令的作用则是让IMC-SRAM开始启动存内计算操作。计算指令被IMC-CP执行后，计算指令中所包含的存内计算操作码和向量长度信息会被IMC-CP分别写入寄存器Roc和Rv中，随后IMC-SRAM中的存内计算流程正式开始。当IMC-SRAM完成存内计算后，将寄存器Rm清零，将IMC-CP切换至普通工作模式，并且通知IMC-SRAM和处理器核切换至同样的工作模式。

下面以图3中的存内向量加法为例来说明存内计算的指令执行过程。为简化起见，将IMC-SRAM的起始地址设为0。对于图3(a)中的实例，只有一个IMC-SRAM模块参与存内计算，那么需要通过存储配置指令将Rn设置为“1”(如果系统刚启动或者复位，也可以不设置)。向量(数组)A， B和C的行地址分别为0， 3和6，存内加法计算的向量长度vl为20，那么完成C =A+B这个向量加法需要执行以下几条指令：

(1) memCfg 1

(2) addrCfg 6， 3， 0

(3) maddu 20

与图3(a)相比，图3(b)中实例的区别在于调用了2个IMC-SRAM模块参与存内计算。因此，完成同样的存内计算，除了Rn的配置不同，其余均与图3(a)中的实例一致。

4 DM-IMCA在物联网信息安全中的应用

随着物联网应用的越来越广泛，其安全性也变得更加重要。因此，非常有必要对所传输的数据进行加密来确保物联网的信息安全。利用加密算法可以有效提高物联网中设备通信时的数据安全。本节将以两个轻量级加密算法为例，介绍DM-IMCA在信息安全中的应用。这两个加密算法分别是一次性密码(One-Time Pad， OTP)[25]算法和哈希算法[26](或称为散列算法)。

4.1 基于DM-IMCA的OTP加密

在OTP加密技术中，信息发送方使用与信息长度一致的密钥对信息进行加密，信息接收方在接收到加密信息后使用与加密时相同的密钥进行解密。由于加解密使用了相同的密钥，因此OTP属于对称加密类型。为保障加密的有效性和安全性，加解密使用的密钥必须为一次性的，即一个密钥只能使用一次。此外，加解密所使用的密钥生成方式应该做到最大限度的随机性。由于OTP技术的密钥长度需要和被加密信息一致，因此其对大文件的加密效率较低，而比较适用于短信息加密。OTP加密的核心过程非常简单，只需对信息内容和一次性密钥做按位异或操作，运算结果便是加密后的内容，如表3所示。

DM-IMCA原生支持异或操作，因此OTP加密过程可直接通过使用IMC指令来实现。将表3中的数组K， P和C在IMC-SRAM中映射的行地址分别设置为32， 40和48，则其字节地址分别为0×400，0×500和0×600。通过DM-IMCA存内计算的方法来实现表3中算法的核心代码如下：

表3 OTP算法

(1) addrCfg 48， 40， 32

(2) mxor N

此处N为各数组的字长信息。如果通过基准系统来实现同样的OTP算法，其汇编代码如下：

(1) li $t0， 0

(2) loop:

(3) lw $t4， 0x400($t0)

(4) lw $t5， 0x500($t0)

(5) xor $t6， $t4， $t5

(6) sw $t6， 0x600($t0)

(7) addiu $t0， $t0， 4

(8) blt $t0， Nb， loop

其中，代码中的Nb=N/4，因为对于MIPS汇编来讲，地址是以字节而不是字为单位计算的。通过上述OTP算法在不同系统中实现的汇编代码对比，也可以看出，相比于传统的冯诺依曼架构的基准系统，DM-IMCA的代码要简洁许多，可以节省大量指令存储器空间。

为了测试与对比，本文搭建了一个测试平台，如图4所示。其中图4(a)是一个作为对照组的基准系统(baseline system)，主要由OpenMIPS、1块大小为32 kbit (128行×256列)的传统6管SRAM宏单元；图4(b)是用于测试的DM-IMCA系统，主要由一个本文改进后的6级流水处理器核M-OpenMIPS、1个大小为32 kbit (128行×256列)的IMCSRAM模块以及协处理器IMC-CP组成。基准系统及D M-I M C A 测试系统均采用由存储编译器(memory compiler)生成的6管SRAM模型作为指令存储器。该平台将用于本文所有应用的测试。

分别选择长度为256 bit(N =8字)和1024 bit(N =32字)的密钥，分别在DM-IMCA和基准系统中进行加密实验。在加密前，明文数组P、密钥数组K和密文数组C在IMC-SRAM中的存储方式类似图3的向量A， B和C。由于在实验中，DM-IMCA只采用了一个IMC-SRAM宏模块，因此N =8时，各数组分别需要占用IMC-SRAM一行的存储空间，而N =32时，各数组占用的IMC-SRAM的存储空间则为4行。分别统计通过DM-IMCA和基准系统进行OTP加密实验所花费的时钟周期数，如图5所示。结果显示，与基准系统相比，利用DMIMCA的存内运算来处理256 bit和1024 bit长度的OTP加密，分别可以获得8.75和23.8倍的运算加速比。

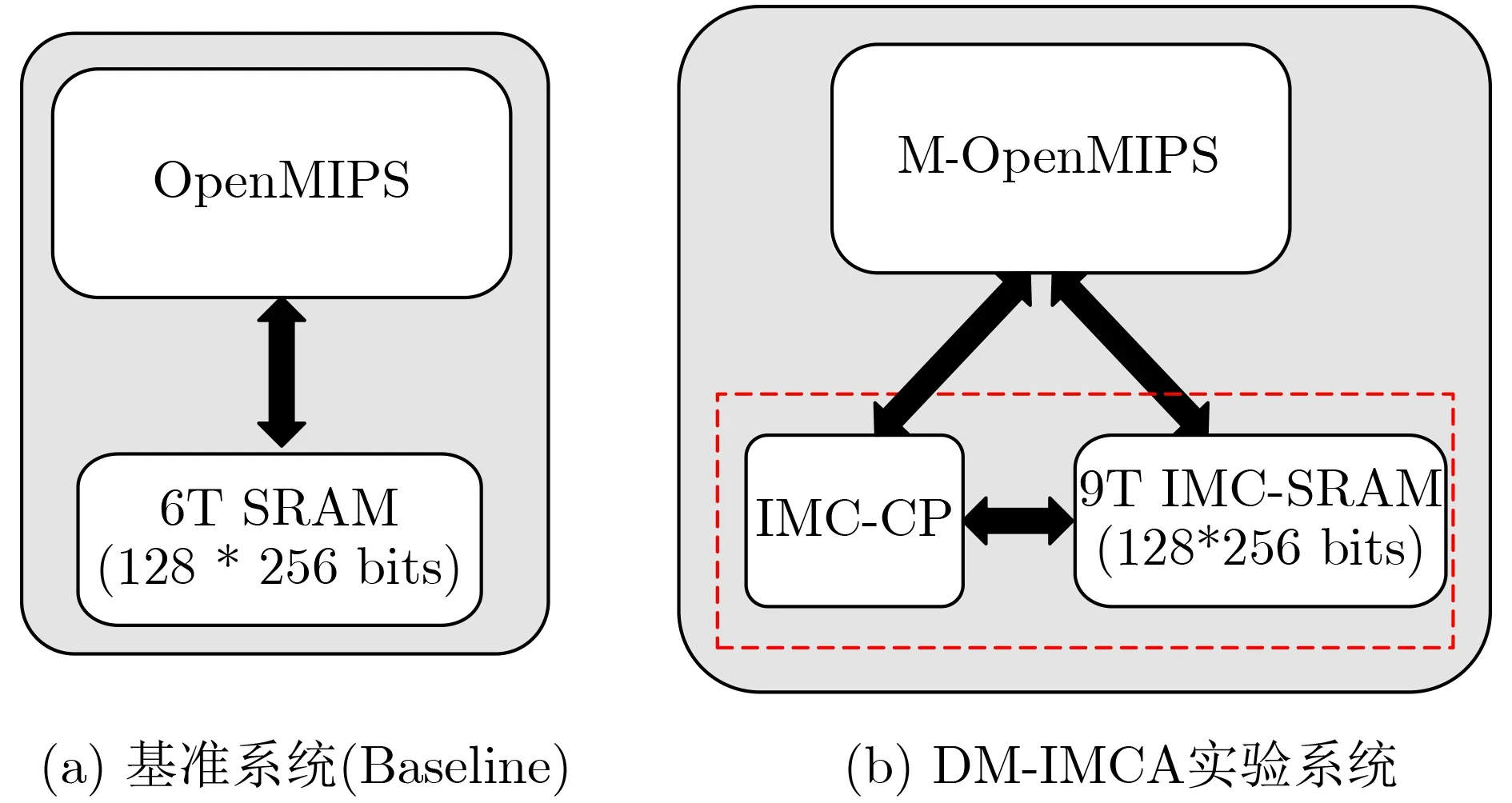
图4 测试平台

4.2 基于DM-IMCA的哈希函数实现

哈希算法的功能是将任意长度的信息映射到固定长度的序列中，这个序列称为哈希值(Hash code)。通常哈希值的长度比信息小得多，且哈希算法的运算是不可逆的，因此常用于信息提炼，以保障信息的真实性。因此信息发送者可以将原始信息和相应的哈希值一起发送，信息接收者通过对接收到的信息进行同样的哈希运算并将结果与接收到哈希值进行对比，来确认收到的信息是否为原始数据。这其实就是常用到的文件校验功能。另一个哈希应用的实例是网站用户登录机制中的密码找回。当用户忘记自己注册的某个网站的登录密码，申请找回密码时，为了保护用户的信息安全，网站管理方不是将登录密码明文发给用户，而是将登录密码的哈希值发送给用户，这样就可以避免密码遭到泄露。除此之外，哈希算法的应用还非常广，例如数字签名、协议鉴权等。随着物联网和区块链的发展，哈希算法在该领域也有着许多应用[27]。

哈希算法实际上是一类算法，而不单指某个算法，常见的MD5和SHA， 以及HMAC等均属于哈希算法的范畴。一般把产生哈希值的函数称为哈希函数，按照哈希值的产生方式不同，哈希函数可以分为加法哈希、乘法哈希、位运算哈希等几种经典的函数。这些基础的哈希函数组合还可以构成更复杂的哈希函数。本节将选取加法哈希在DM-IMCA以及基准系统中进行实现。加法哈希的描述如表4所示，其中key和len分别表示输入的字符串和字符串长度，prime是任意的质数。

图5 测试OTP加密所花费的时间对比

表4 加法哈希算法

从表4可以看出，加法哈希函数运算的核心部分实质是一个加法树，其规模随着字符串长度的增加而越来越庞大。这样的运算在基准系统中实现只能是以串行的方式逐个进行累加，显然效率较低，耗时较长。在DM-IMCA中，可以将字符串数组映射于IMC-SRAM中，按存内计算的存储要求排列，分批次进行运算。假设字符串长度len=128时，字符串数组key在IMC-SRAM中的起始地址为0×400(行地址为32)。先将数组key的元素对半分为两个新的数组K1和 K2，并分别按如图6所示的方式依次存储于IMC-SRAM中(需要注意的是，由于当前IMC-SRAM不支持字符型数据的操作，因此需将char型数据转换为unsinged int型)。K1和K2通过存内加法进行各元素相加，并将结果存于K1中，即

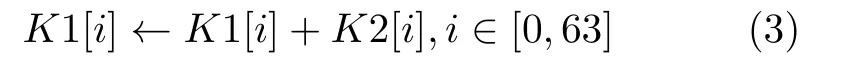
按式(3)完成第1阶段运算后，接着用同样的方法将数组K1对半分为两部分，分别记为K3和K4，再通过存内计算执行如下操作：K3[i]←K3[i]+K4[i]，i ∈[0，31]。以此类推，反复进行同样的数组对半拆分操作及存内加法运算，直到无法使用存内运算进行加法操作，将剩下的元素取出至处理器核中进行相加。对于字符串长度len=128的实例，存内矢量加法运算的相关汇编代码如下：

(1) addrCfg 32， 40， 32

K1[i]←K1[i]+K2[i]，i ∈[0，63]

(2) maddu 64 //

(3) addrCfg 32， 36， 32

K3[i]←K3[i]+K4[i]，i ∈[0，31]

(4) maddu 32 //

图6 加法哈希函数运算中字符串在IMC-SRAM中的映射

(5) addrCfg 32， 34， 32

(6) maddu 16

(7) addrCfg 32，33， 32

(8) maddu 8

分别取长度len为256和512的字符串使用加法哈希算法在基准系统和DM-IMCA中进行试验，并统计各自所消耗的时钟周期数，其结果如图7所示。结果显示，与基准系统相比，使用DM-IMCA的存内运算功能进行长度为256和512位字符的加法哈希加密运算分别可以获得约6.5倍和12.2倍的运算加速比。通过图7还可以看出，随着数日字符串长度翻倍，基准系统所需的加法哈希运算时间也几乎翻倍，而使用DM-IMCA来运算增加的时间非常少。因此，字符串越长，使用DM-IMCA进行加法哈希运算越有优势。

5 DM-IMCA在深度神经网络中的应用

图7 测试加法哈希算法进行加密所耗费的时间对比

近些年来，随着集成电路工艺的发展，计算机的算力获得了巨大提升。此外，在信息化时代，社会所产生的数据呈爆炸式增长。这些因素极大地促进了人工智能技术的快速发展，从而使人工智能得到了极广泛的应用，包括热门的计算机视觉、语音识别，以及自然语言处理[28]。在众多的人工智能模型中，卷积神经网络(Convolutional Neural Networks， CNNs)的发展尤其成功，例如著名的LeNet-5[29]， VGGNet[30]和ResNet[31]，均属于CNN。然而，CNN对存储和计算资源有着巨大的需求，例如VGG-16网络需要存储138 MB的参数，为了对一幅大小为224×224的图像进行分类，需要进行高达15.5 G次的浮点精度MAC(Multiply-Accumulate)运算；ResNet-50也仍然需要存储25.5 MB的参数，对同样大小的图片进行分类，需要高达3.9 G次的浮点精度MAC运算。对于面积和功耗等资源紧张型的场景，如嵌入式设备或移动终端，以及物联网中的许多边缘设备，这样的原生网络实在过于庞大，不便于部署。庆幸的是，Courbariaux等人通过研究证明可以同时将权值和神经元激活(neuron activations)二值化，即同时减小到1 bit精度，同时不会遭受明显的分类精度损失[32，33]。例如，可以采用如式(4)所示的算法进行二值化。

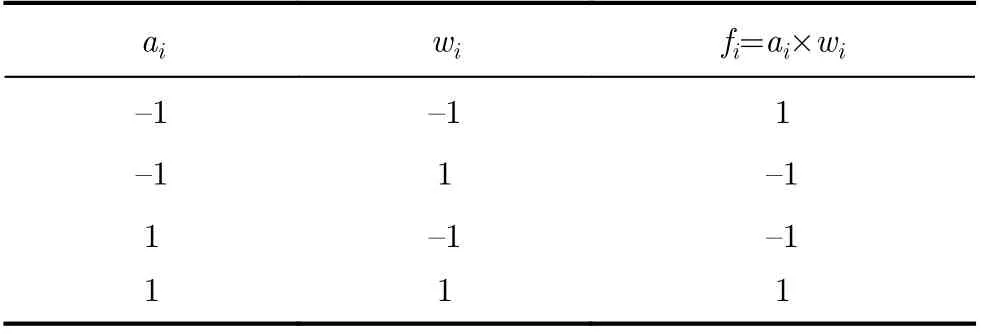
表5 二值乘法真值表

将神经网络的权值和激活二值化可以极大地压缩参数所需的存储空间，节省硬件计算资源。此外，功耗也相应得到大幅度降低[32]。

式(6)中的xor运算可以通过DM-IMCA中高度并行的mxor指令来实现存内计算，操作类似前述的OTP加密运算；此外，popcount操作也可以通过移位和加法等多类存内运算组合来完成。为了充分利用IMC-SRAM存储空间，首先将向量a和W 的元素以字为单位合并后存储于整形数组中。图8所示的是当向量长度L=256时，激活a和权值W 的存储映射实例。 a和W 分别映射到数组A和B中，并在IMC-SRAM中按行对其排列。其次，利用存内运算来完成XOR操作。随后分别通过移位、数据位屏蔽以及加法来完成popcount操作。表6描述了popcount(xnor())操作在IMC-SRAM中的存内运算映射，其中第(3)行描述的是XOR操作，第(4)～(11)行描述的popcount操作。第(4)， (5)，(6)和(8)行描述的运算分别可以通过DM-IMCA中的mxor， mand， maddu和msr指令来实现并行运算。表6中算法中涉及的数组M， C和D在IMCSRAM中的存储映射如图8所示。若输入数组A和B的长度较大，第(12)～(14)行操作还可以使用存内加法进一步进行加速，类似前面所介绍的对哈希算法中的加法树运算。

表6 存内矢量XOR运算和popcount操作算法

设数组A， B， M， C和D在IMC-SRAM中的行地址分别为32， 40， 48， 56和64，当L=256时，在DM-IMCA中实现表6中算法中的第(4)～(11)行运算的汇编代码如下：

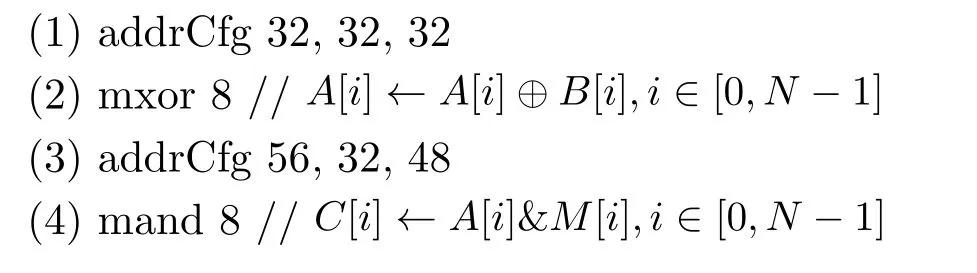
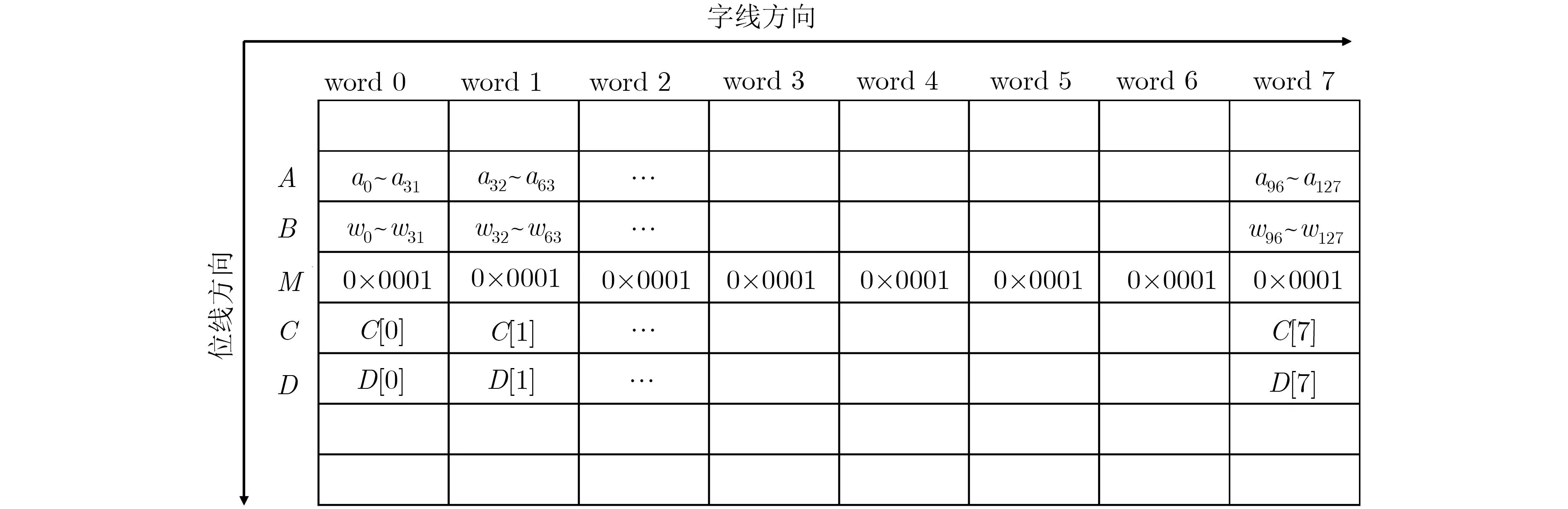
图8 二值神经网络中激活和权重在IMC-SRAM中的映射

而在基准系统中实现相同的功能，各步的运算都只能使用串行操作，因此运算效率将会比在DMIMCA中实现更低。

在实际的二值神经网络中，通常存在多维度的卷积操作，从而使参与MAC运算的两个向量长度均比较长。因此，对应的二值卷积计算中a和W的向量长度也较长。本节将通过实验模拟较长的二值卷积计算，从而观察DM-IMCA存内运算对其的加速效果。分别取向量a和W的长度L=512，L=1024和L=2048，分别在基准系统和DM-IMCA系统中实现，最后统计各自所消耗的时钟周期数，结果如图9所示。经计算可知，相比于基准系统，采用DM-IMCA实现长度L=512， L=1024和L=2048二值卷积运算，分别可以获得7.7倍、12.4倍和17.8倍的运算加速比。

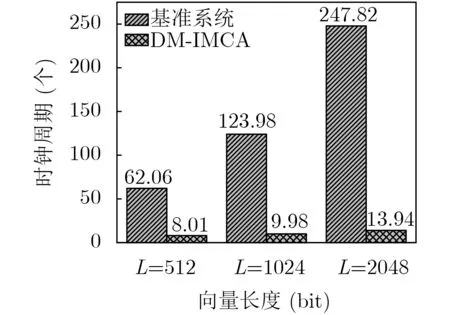
图9 测试二进制卷积运算所花费的时钟周期数对比

6 DM-IMCA在图像处理中的应用

除了在信息安全和卷积神经网络领域，DMIMCA在其他领域也存在着潜在的应用价值，例如传统的图像处理和视频处理领域。本节将简单介绍DM-IMCA在图像灰度化处理中的应用，以期能够对DM-IMCA在其他方面的应用起到启发作用。

在计算机图形学中，每幅图像使用一个2维数组表示，数组中的每个元素均表示一个像素点(Pixel)。根据像素点表示的不同，图像可以分为多种类型：真彩色图像、索引图像、二值图像和灰度图[34]。其中二值图像的每个像素点仅在“0”和“1”中取值，因此图像只有白和黑两种颜色。灰度图像是每个像素只有一个采样颜色的图像，每个像素点在[0， 255]范围内取值，0～255中间的每个值都代表了一个级别的灰度。因此灰度图像体现的是一幅图像中各区域的颜色深浅。真彩色图像也称为RGB图像，每个像素点由红(R)、绿(G)和蓝(B)3个分量来按不同灰度叠加构成，每个分量取值均在[0， 255]范围内。真彩色图像能够更真实地表达现实世界，因此在日常生活中我们通常使用彩色图像来记录事物。然而在很多场景中，灰度图像依然有着非常广泛的应用。例如黑白印刷由于比彩色印刷更廉价，依然受到大众欢迎。在打印中通常需要将彩色图像转为灰度图像，并对图像的灰度进行增强以提高打印品质。另外，在图像的边缘检测、特征提取、图像分割及图像分类等图像处理过程中也经常使用灰度图像，因为相比于彩色图像，灰度图像数据量小，便于存储和提高运算效率。因此使用这些算法进行图像处理之前，经常需要预先将彩色图像转换为灰度图像。

因此，通过位宽量化及精度缩减，可以将图像灰度化公式变换成只包含加法和移位运算。例如式(11)中的2×Gm×n可以通过DM-IMCA的一次加法(m a d d)或者移位(m s r l)实现，式(1 2)中的5×Gm×n可以通过DM-IMCA的两次存内1 bit移位及一次加法实现。对于一个像素点来说，若使用式(11)来将RGB值转换为灰度值，需要通过4次存内运算来完成。一般图像由比较大的像素点阵(如16×16， 64×64或256×256)组成，图像灰度化运算量比较大。但由于DM-IMCA支持自动化及自适应的存内向量计算，仍然可以对图像灰度化运算提供可观的加速比。对一幅像素为28×28的RGB图像进行灰度化，实验结果表明，对于相同的量化后算法，相比于基准系统，在DM-IMCA中实现可以获得约10倍的运算加速比。

7 结束语

本文介绍了基于SRAM进行存内逻辑计算的原理，以及基于SRAM的通用存算一体架构平台DMIMCA。随后，本文选取了OTP加密、哈希算法、二值深度神经网络以及图像灰度处理等几个轻量级物联网应用，对其进行算法分析及拆分，将数据密集计算部分算法映射到一款通用型存算一体架构平台DM-IMCA的计算型SRAM中，以达到对应用进行加速和提高能效的目的。这些实例表明DMIMCA在物联网领域具有较高的应用价值，且为后续的应用提供了思路与方法。