粗糙裂隙局部流场可视化实验教学探索

郭平业， 王 蒙， 刘世童， 高 恺

（中国矿业大学（北京）力学与建筑工程学院；深部岩土力学与地下工程国家重点实验室，北京 100083）

0 引 言

裂隙渗流问题是水利、石油、矿业等工程领域面临的关键科学问题之一［1-3］，常规的裂隙渗流实验多参照经典的Darcy渗流实验，通过实验获取不同条件下流量或流速与压力梯度之间的关系，并依据实验结果验证或修正各种理论与经验公式。但常规渗流实验受限于岩石样品的不透光性，无法观测裂隙内部流场结构特征的演化过程，仅能获得样品进口和出口两端的宏观流动参量变化规律，缺乏宏观流动参量关联式与裂隙内部流场演化过程的有效结合。而对于粗糙裂隙渗流的非线性特征研究，除了分析宏观流动参量的变化规律，更需要关注裂隙内部局部流场结构演化过程，因此流动显示实验就显得尤为重要。随着现代光学、摄像和计算机图像处理技术的飞速发展，流动显示方法得到很大改进，已从定性走向定量化，流动显示实验在流体力学研究中的比重逐渐增大。在流动显示教学方面，基于粒子图像测速（PIV）技术的流动显示教学案例较为广泛，在船舶尾部流场等宏观流场测试分析中取得良好的教学效果［4-8］。另外，随着光学测试技术的发展，微观粒子图像测速（Micro-PIV）技术已成为局部微观流场测量的主要方法，其拥有较高的分辨率及测量精度、强大的图像及数据处理能力。同时，利用3D打印和激光刻蚀等技术可获得不同条件的透明裂隙模型，使得粗糙裂隙局部流场可视化实验成为可能［9-11］。

为响应国家深化教育改革的号召、提高工程流体力学实验教学质量、增强学生学习兴趣和实验能力［12-13］，引入Micro-PIV技术进行裂隙渗流实验教学改革。通过理论知识与实验实操相结合的方式［14-15］，激发学生的学习热情、让学生更好的理解理论知识，同时也能够推动实验研究，培养创新型人才。针对裂隙非线性渗流问题，以Navier-Stokes（N-S）方程为出发点，讲解各种理论或经验公式的物理意义、简化推导及适用条件，然后，通过流动显示实验平台进行粗糙裂隙局部流场可视化实验，建立“知识体系——理论推演——实验教学”的授课方法，提高学生学习兴趣的同时加强授课质量［16-17］。

1 裂隙渗流可视化实验教学的主要知识体系

如图1所示，裂隙渗流可视化实验教学的主要知识体系包含N-S方程、量纲分析方法、传统裂隙渗流实验、雷诺实验和流动显示实验方法。教学中首先讲解N-S方程各项组成及物理意义，然后利用量纲分析的方法，依据各类裂隙渗流模型的假设条件简化N-S方程，从理论上推导包括Darcy定律、立方定理在内的各种裂隙渗流模型。同时，介绍裂隙渗流相关的实验方法，包括常规渗流实验、雷诺实验和流动显示实验。其中，通过常规渗流实验的讲解使学生首先掌握经典的Darcy渗流实验，而回顾雷诺实验使学生更进一步理解不同的流动状态和N-S方程的物理意义。在流动显示实验方面，在介绍包括悬浮物法、烟线法等常规传统的流动显示技术基础上，重点讲解目前常用的PIV技术。以上知识体系设置使得基础理论和实验方法有机结合，教学过程中学生不仅可以通过实验验证或修正理论模型、公式等，还可以激发学生应用理论知识揭示探索实验中新的现象和规律。

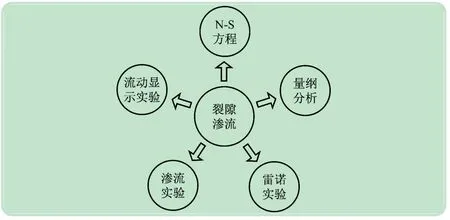
图1 裂隙渗流可视化实验知识体系图

2 裂隙渗流理论推演

在开展实验教学前，先开展裂隙渗流相关的基础理论讲解，图2所示为裂隙非线性渗流问题中基础理论模型与实验研究间的逻辑关系图。首先，围绕N-S方程组，结合量纲分析方法，针对具体的适用条件，讲解N-S方程简化为Stokes方程、Reynolds方程、Couette流动模型、Hagen-Poiseuille公式、Darcy公式和立方定理等的详细推导过程。明确指出上述方程或公式的适用条件，多数仅能描述雷诺数较低的流动，在高雷诺数条件下无法很好地描述裂隙内流体的流动行为。在此基础上，结合最新的研究进展和文献资料，介绍粗糙裂隙非线性流动现象，同时，引入常用的描述粗糙裂隙非线性流动行为的两个经验公式：Forchheimer与Izbash公式，并通过常规裂隙渗流实验验证上述非线性流动描述公式。最后，指出Forchheimer、Izbash等描述非线性流动的公式和常规裂隙渗流实验的局限性，即没有考虑裂隙内部流场的涡旋等非线性结构特征，从而引入现代流动显示实验方法，重点讲解PIV流场测试技术。通过理论教学，使学生回顾流体力学基本方程的推导和应用，掌握量纲分析方法，了解粗糙裂隙常规渗流实验和局部流场可视化实验方法。

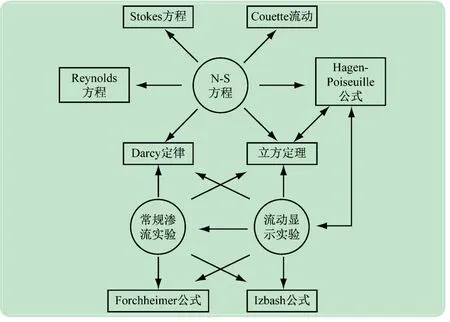
图2 裂隙渗流理论模型与实验之间的逻辑关系图

为了让学生们在实验过程当中能够更加清楚地将理论知识与实验结果相结合，通过量纲分析的方法推导N-S方程，为学生们详细介绍了图2中各公式之间的关系，此处仅介绍部分公式推导。

量纲为1的N-S方程推导。对于不可压缩流体，当体积力仅考虑重力时，N-S方程为：

将上式化为量纲为1的方程，引入特征速度、特征长度、特征时间、特征压力，这些特征量视具体情况选取：

将式（2）代入式（1）中整理得到：

式（3）中存在4个量纲为1的参数：

将4个参数代入式（3）中得：

再用式（4）求解实际流场时，可通过比较方程中4个参数的大小，忽略量级小的项，使方程得以简化而便于求解。

当流量较小时，惯性项相对于粘性项可以忽略，N-S方程可以简化为Stokes方程：

更进一步，Stokes方程可以简化为一维形式的Reynolds方程：

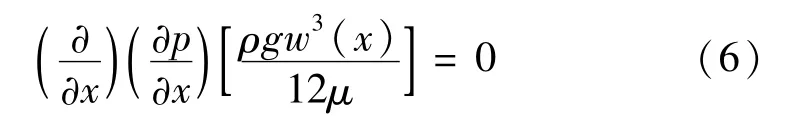
式（6）通过积分就可得到工程上广泛应用的立方定理：

以上内容重点讲解公式的物理意义和适用条件，在此基础上，结合裂隙常规渗流实验，介绍通过实验拟合的两个描述裂隙中非线性流动的经验方程，式（8）为Forchheimer方程，式（9）为Izbash方程。

式中：λ和m是Izbash方程的系数。m的值在1到2之间变化。当m＝1时，上式可简化为Darcy定律，流动符合层流状态。当m＝2时，Izbash方程可以很好地描述了多孔介质中的非线性渗流。

3 实验教学

实验教学主要目的是为了让学生们更好地理解裂隙渗流中的理论知识，提高学生的研究兴趣及动手能力。教学实验结合裂隙非线性渗流的热点问题，基于N.Barton提出的10条节理裂隙粗糙度标准剖面轮廓曲线（JRC）制作粗糙裂隙流动可视化模型，通过Micro-PIV技术分层次、分阶段进行实验教学。

基于Micro-PIV的粗糙裂隙流动可视化实验平台系统图如图3所示，可视化实验平台主要包括：安装了分析软件的计算机，532 nm双脉冲激光器，显微镜，CCD相机，注射泵，测压计及可视化裂隙模型。

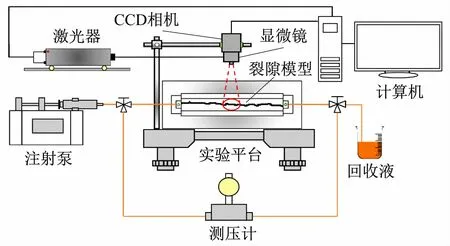
图3 粗糙裂隙可视化实验平台系统示意图

详细教学实验流程如图4所示，实验教学过程如下：

(1)开展基础实验教学。学生通过观看实验操作流程，了解Micro-PIV实验设备、粗糙裂隙流动可视化实验原理及实验步骤，观察已有的实验结果并与前期课堂教学的理论知识相结合，加深学生对非线性流动、流线、雷诺数、层流、紊流及涡流等流体力学知识的理解。

(2)进行综合实验操作练习。学生在实验员的指导下亲自动手进行简单的平行板模型流动可视化实验，记录不同流速下模型进出口压力差，并通过Darcy定律、立方定理、非线性流动方程等理论公式进行拟合及理论分析；观察不同流速下平行板模型内部流态，通过Micro-PIV记录并分析某一时刻下局部流场，得到沿模型隙宽方向的速度分布曲线，与Hagen-Poiseuille公式求得的理论解进行对比分析。通过亲自动手进行实验，进一步加深学生对实验原理及理论知识的理解，激发了学生进行实验研究探索的兴趣。

图4 粗糙裂隙可视化教学实验流程图

(3)进行深入实验研究。经过前两个阶段的实验教学与实际操作，学生已基本掌握了所学的流体力学知识及流动可视化实验方法，为了激发学生的主观能动性及科研潜力，鼓励学生基于10条节理裂隙粗糙度标准剖面轮廓曲线进行独立自主的实验研究，进一步巩固所学的理论知识、实验原理及操作流程。

实验教学中，要求学生重点观测裂隙局部流场随雷诺数增大的变化过程，定量分析裂隙速度分布随雷诺数的变化规律，观测裂隙局部流场内涡流等非线性结构的产生与发展过程（见图5）。同时，要求学生通过Darcy定律、立方定理、非线性流动方程等理论公式拟合裂隙渗流实验结果，结合可视化实验获得局部流场特征演化过程，分析粗糙裂隙宏观流动参数与局部流场特征演化的关联性，探寻裂隙内非线性流动的规律、影响因素及机理，进而引导学生进入更深的研究领域。

4 结 语

图5 不同雷诺数时的裂隙局部流场特征

理论知识与实验操作结合的教学方式一直是工科专业授课的核心方式。通过将Micro-PIV技术引入流体力学实验教学，与研究热点粗糙裂隙非线性流动问题相结合，采取“基础教学—综合练习—深入研究”分层次、分阶段的教学方式将理论知识与实验操作串联在一起，解决了常规裂隙渗流实验中无法获取流场信息的问题，让学生们进一步理解了流线、雷诺数、层流、紊流、涡流等知识点，掌握了流体力学基本方程的应用及场测试技术的基本原理和操作流程。通过该实验教学改革，不仅开阔了学生眼界、提高了学习兴趣和动手能力，也丰富了相应的教学手段，为传统教学方式注入了新的生机与活力，提高了教学质量和效果。