输油管道生产运行参数优化
李文忠 王兴旺 郑立龙 魏立新,4
(1.大庆油田有限责任公司储运销售分公司;2.中国石化石油勘探开发研究院;3.东北石油大学石油工程学院;4.中国石油天然气集团公司油气储运重点实验室)
某输油管道属于热油输送管道,输送介质为庆油和俄油按一定比例的混合原油。为了保证安全输送,输送过程中需要对油品进行升温加压。不同的输送温度和压力直接影响着运输成本。为了保证管道安全经济输送,管道最佳运行方案应与管道运行工况相匹配。
针对输油管道,戚广彪等人[1]运用优化出站温度温度的方法达到节能降耗的目的;易旸[2]也运用遗传算法、粒子群算法和模拟退火算法优化算法优化了对庆铁四线进行优化,达到减小成本的目的;魏立新,陈明辉等人[3]采用遗传算法和惩罚函数法对油田注水系统进行优化,在实际应用中取得了良好的效果;魏立新,刘扬等人[4]运用二级阶梯优化方法对输油管道系统进行优化,降低了能耗,效果明显;孙胜戈,唐愚等人[5]运用线性规划法对输油管道进行优化求解;倪玲英,李成华[6]根据分析影响成本的因素运用编制的软件对输油管道优化方案进行优化;张维志,王兰花等人[7]利用组合优化方法对长输热油密闭输油管道进行优化,优化效果明显;张维志,于清澄等人[8]运用动态规划法对运行优化方案机进行求解。
针对某输油管道的特点,以总能耗费用最低为目标建立了给定输量和设备开启方案下的系统运行参数优化优化模型,并给出高效求解策略。
1 优化数学模型
在给定输油量、设备开启方案、混油比等的条件下,影响管道总能耗费用的主要参数是输送温度和输送压力[9]。因此,以输油温度、输油压力为设计变量,以总能耗费用最低为目标,以输量约束、温度约束、压力约束、站场加热能力约束、站场的加压能力约束、输油泵工作性能约束和加热炉加热能力约束为约束条件,建立生产运行参数优化的数学模型如下:
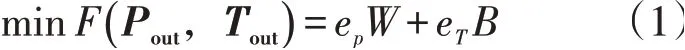
其中:
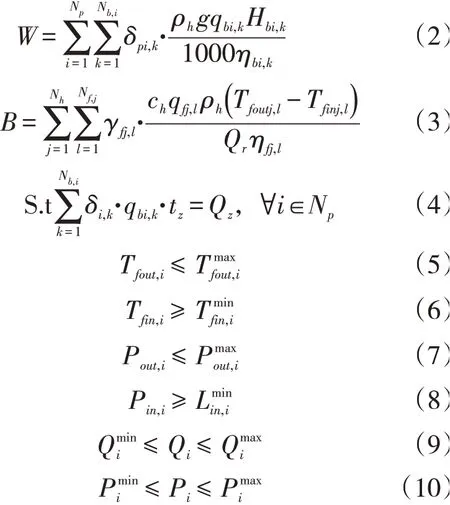
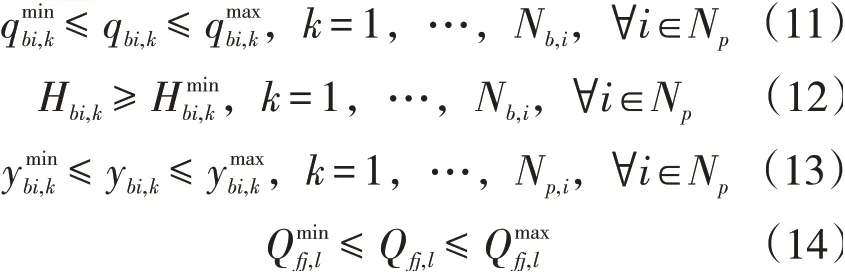
式中:Np为输油管道泵站个数;Nh为输油管道热站个数;Nb,i为第i泵站输油泵的总数;Nf,j为第j热站加热炉的总数;Pout为各泵站出站压力向量;Tout为各热站出站温度向量;B为输油管道全线加热炉总燃油消耗量,t;W为输油管道全线输油泵总耗电量,kWh;eP为单位电费价格,元/kWh;eT为燃料单位价格,元/t;δbi,k为第i泵站第k台泵的运行状态,0为关闭、1为开启;ρh为混合原油密度;qbi,k为第i泵站第k台泵的输量;Hbi,k为第i泵站第k台泵的扬程,m;ηbi,k为第i泵站第k台泵的泵效;γfj,l为第j热站第1台加热炉的运行状态,0为关闭、1为开启;ch为混合原油比热容,kJ/(kg·℃);Tfoutj,l为第j热站第1台加热炉的出口温度,℃;Tfinj,l为第j热站第1台加热炉的进口温度,℃;Qr为燃料油燃烧产生的热值,kJ/kg;ηfj,l为第j热站第1台加热炉的效率;tz为总的调度时间,h;Qz为tz时间内管道的任务输量,t;为允许最低进站油温,℃;为最高出站油温,℃;为第i站的最高出站压力,MPa;为第i站的最低进站压力,MPa;Qi为第i站的加热能力,kJ;Qmax
i为第i站的最大加热能力,kJ;为第i站的最小加热能力,kJ;Pi为第i站的加压能力,MPa;Pmaxi为第i站的最大加压能力,MPa;为第i站的最小加压能力,MPa;为第i站第k台输油泵的最高排量,m3/s;为第i站第k台输油泵的最低排量,m3/s;为第i站第k台输油泵汽蚀余量,m;为第i站第k台输油泵最小汽蚀余量,m;为第i站第k台输油泵高效运行时的最低转速,r/min;为第i站第k台输油泵高效运行时的最高转速,r/min;为第j热站第1台加热炉高效运行的最高热负荷,kJ;为第j热站第1台加热炉高效运行时的最低热负荷,kJ。
在上述约束条件中,约束条件式(4)为输量约束,一定时间内多台泵并联时,并联泵流量之和等于总输量;约束条件式(5)~(6)为温度约束,输油温度应在一定范围之内;约束条件式(7)~(8)为压力约束,输油压力应在符合设备要求,在一定范围之内;约束条件式(9)为站场加热能力约束,每个站场加热能力不同,应在合理范围之内;约束条件式(10)为站场加热能力约束,为使站场在高效区内;约束条件式(11)~(13)为输油泵工作性能约束,为使输油泵高效运行,其输量、扬程和转速应在合理范围之内;约束条件式(14)为加热炉工作性能约束,根据加热炉的实际情况,加热炉的热负荷应在合理范围之内。
2 求解算法研究
某输油管道生产运行参数优化问题是包含多个约束条件的非线性优化问题。针对此问题,有许多学者提出群体优化策略,如粒子群算法、蚁群算法和鸟群算法等智能优化策略。但这类优化策略都是处理无约束问题的方法,处理此问题还需要有约束问题处理成无约束问题,比较复杂。因此,针对此模型的特点,采用序列二次规划法进行求解。
又因为序列二次规划法[10],理论上只具有局部收敛性,为了能收敛到最优解,必须选择与真解充分接近的初始点。但是事先是难以得到好的最优解推测值的。所以对方法加以改良,使之不管从哪个初始解出发,都一定会收敛到某个局部最优解。即使之具有整体收敛性。下面就介绍一种通过罚函数[11]进行一维搜索来保证序列二次规划法具有整体收敛性的方法。
所谓罚函数是由目标函数和反映可行性程度的一个指标相结合的函数。这里,对于该问题,采用如下形式的罚函数:
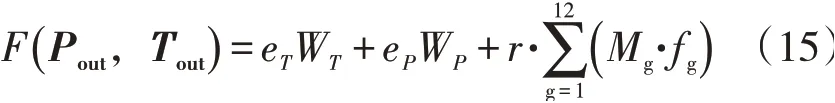
其中:
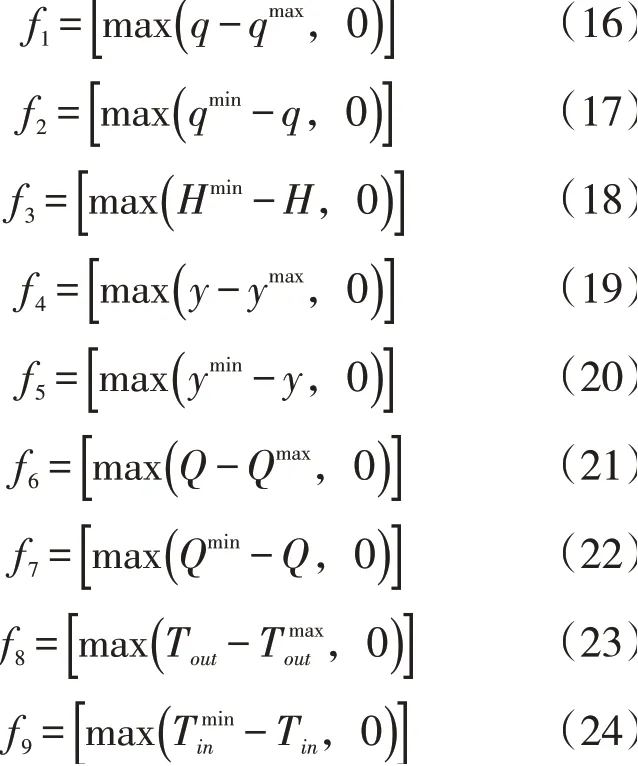
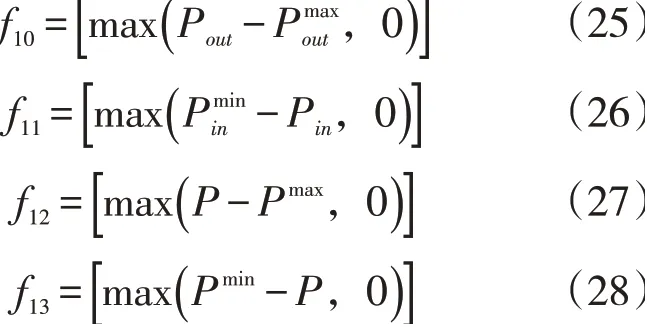
式中:r为惩罚因子。
通过罚函数进行一维搜索来保证序列二次规划法具有整体收敛性的方法,改进了序列二次规划法的不足,提高了计算精度。序列二次规划法程序见图1。
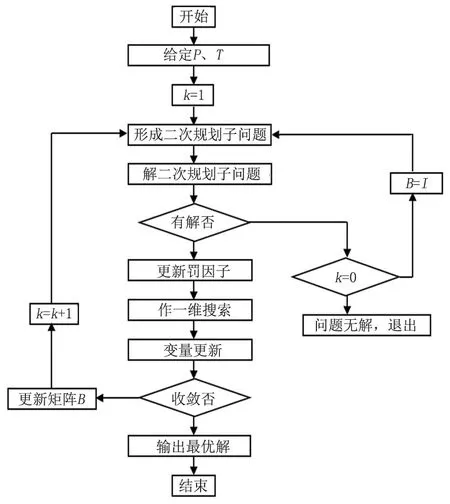
图1 序列二次规划法程序
3 计算实例
采用序列二次规划法对某一时间内某输油管道生产运行参数进行了优化。管道输量为9935t/d,庆油和俄油混合比例1∶1.63,电价为0.637元/kWh,燃油单价为2.102元/kg。首站、中一站和中二站均开启1台输油泵和1台加热炉。优化前后其各站输油温度、输油压力、耗电量、燃油消耗量及总能耗费用对比见图2~图5。
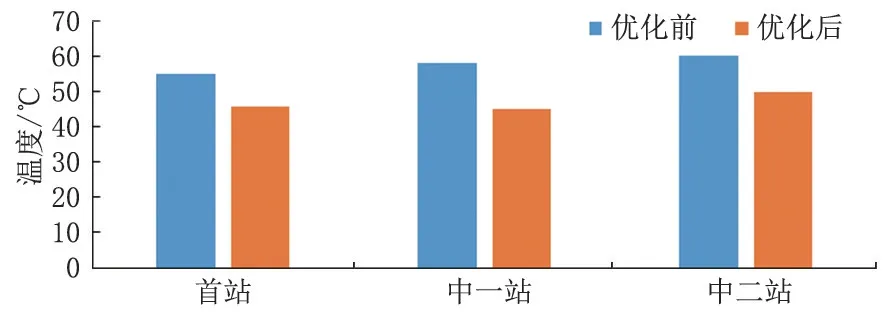
图2 优化前后各站输油温度对比
优化后各站输油温度降低,输油压力升高,由于输油温度降低,使原油黏度升高,进而使输油压力升高;优化后各站耗电量分别增加了6.8%、17.7%和17.6%;各站燃油消耗量分别降低了35.1%、66.3%和45.5%;总燃油费降低了19187.06元,节省了46.7%;总电费升高了4233.01元,增加了12.3%,总费用降低了14954.05元,节省了19.8%。优化效果显著。
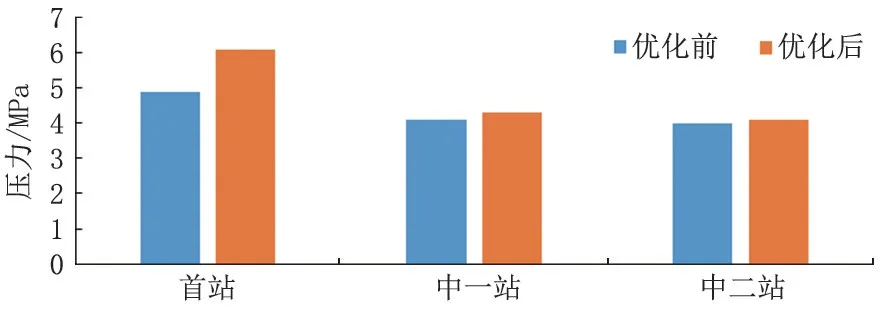
图3 优化前后各站输油压力对比
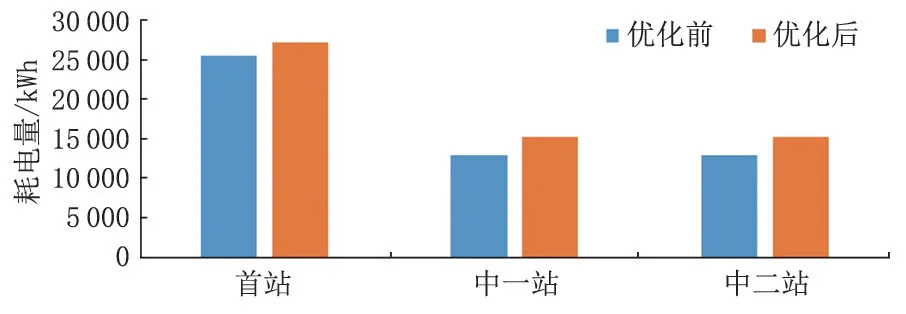
图4 优化前后各站耗电量对比
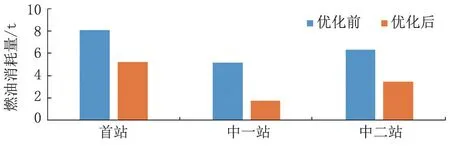
图5 优化前后各站燃油消耗量对比
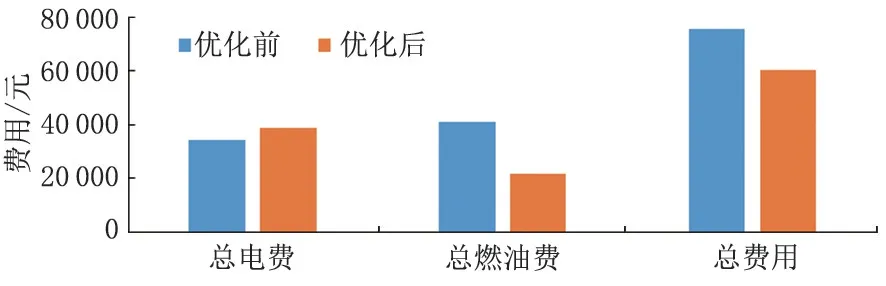
图6 优化前后各项费用对比
4 结论
1)根据实际生产需要,建立了以总能耗费用最低为目标,以输量约束、温度约束、压力约束、站场加热能力约束、站场的加压能力约束、输油泵工作性能约束和加热炉加热能力约束等为约束条件的某输油管道生产运行参数优化的数学模型,并给出序列二次规划法的求解策略。
2)对某输油管道生产运行参数进行优化计算。优化后总燃油费降低了46.7%,总电费增加了12.3%,总费用节省了19.8%,优化效果显著。

