多分区响应型接驳公交路径与发车时间的协调优化

王正武 ，谭笑 ，高愿 ，程向昕

(1.长沙理工大学 交通运输工程学院，湖南 长沙 410114；2.长沙理工大学 智能道路与车路协同湖南省重点实验室，湖南 长沙 410114)

为解决轨道公交等干线公交换乘站周边区域乘客出行的“最后一公里”问题，响应型接驳公交(Responsive Feeder Transit，RFT)被提出。目前，RFT 系统已成为智慧公交的研究热点之一，吸引了许多学者的关注。如QIU 等[1]比较分析了灵活公交、半灵活公交、固定公交的服务性能；ZHENG等[2]比较分析了低密度居民区域灵活公交的路线偏移和站点偏移策略；PAN 等[3−4]建立不规则服务区域RFT 的混合数规划模型来进行路径优化；韩博文等[5−6]均考虑既有静态需求、也有动态需求的需求响应公交，构建了两阶段调度优化及其启发式求解算法；YU 等[7]探讨了实时需求下循环接驳公交的线路优化问题；王力生等[8]运用图论和动态规划方法分别构建了RFT 路径优化模型；邓连波等[9]构建了常规接驳公交的线网优化模型；FERNAN‐DEZ 等[10]提出基于网络设计来优化需求响应公交的车辆路径；王正武等[11−12]构建了多换乘站和多车场协调的路径优化模型；王正武等[13]构建了同时接送模式RFT 系统车辆路径与发车时间的协调优化模型；王正武等[14]构建了RFT 分区内的路径协调优化模型；CHANDRA 等[15−19]分别从服务质量、票价、运营成本、乘客满意度、乘客利益、运营商利润、系统成本、票价收入、乘客数、乘客出行时间、车辆运行时间等中选择一个或多个指标构建目标函数来优化车辆路径或调度。到目前为止，现有研究主要关注的是一个分区的RFT 系统，很少考虑对较大服务区域进行划分，按分区优化车辆路径与调度[14]；几乎没有考虑边界上需求的协调分配，实际上，边界上乘客需求归属的分区不同，各分区的车辆路径与调度方案就不同；而且，很少考虑乘客满意度、运营商利润等的冲突，构建多目标优化模型获取Pareto 最优解来供管理者决策。针对上述问题，本文以多分区RFT 系统为研究对象，同时考虑分区边界上的、分区内的预约需求，兼顾运营商利润、乘客满意度，构建预约需求下RFT 系统多分区协调的、车辆路径与发车时间协调的多目标优化模型，从而有效提高RFT系统的运行性能。

1 多目标协调优化模型的构建

1.1 问题描述

在包含Z个分区的RFT 系统中(如图1 所示)，其分区已划定，且边界线已知；乘客预约需求点的集合为I(换乘站编号为0)，所有需求点i∈I的坐标(xi,yi),乘客数ni,可容忍时间窗[ETi,LTi],预约时间窗[eTi,lTi],预约上车时间(eTi+lTi)/2均已知；车内乘客的可容忍等待时间为Emax；分区边界上需求点的集合Ib,分区z内需求点的集合为Iz,I=Ib∪Iz，在满足乘客时间窗、车辆容量等约束下，通过分区边界上乘客的合理分配、车辆路径和发车时间的优化，同时尽量使乘客满意度、运营商利润最大。

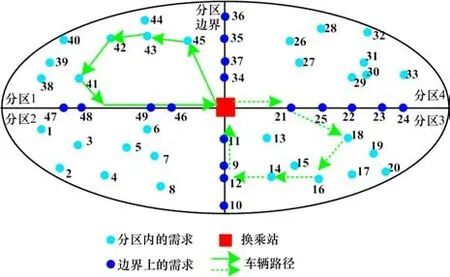
图1 多分区RFT系统示意图Fig.1 Schematic diagram of multi-partition RFT system

1.2 基本假设

1) 乘客只能在预约需求点上车，在换乘站下车(只考虑接，送是其逆过程)；

2)乘客需求一旦被系统响应便不会取消预约；所有乘客均在预约上车时间到达需求点，当乘客上车后接驳车辆立即发车；接驳车辆沿需求点间的最短路行驶，其运行速度恒为V；

3) 所有需求均应被响应，同一需求点只能被服务一次；如果车辆提早到达需求点则需在需求点等待乘客上车；同一需求点内乘客的预约时间窗相同且都为软时间窗，不同时间窗的乘客属于不同的需求点。

1.3 模型构建

乘客满意度是乘客对公交服务满意程度的衡量，本文以车辆到达需求点和换乘站的准时性作为衡量指标。一般地，车辆若提早到达需求点i，则需在需求点i等待乘客上车，车内乘客的满意度随等待时间的增加而降低；若车辆晚点到达需求点i，则需求点i乘客需等待上车，上车乘客的满意度也随等待时间的增加而降低。设分区z班次k开始服务需求点i的时间为Tikz；yikz∈{0,1}，若分区z班次k服务需求点i则为1，否则为0。需求点i的乘客满意度Sikz是车上乘客满意度S1ikz和上车乘客满意度S2ikz。若车辆早到，则车上乘客等待；若车辆晚到，则上车乘客等待。故根据文献[5]有：

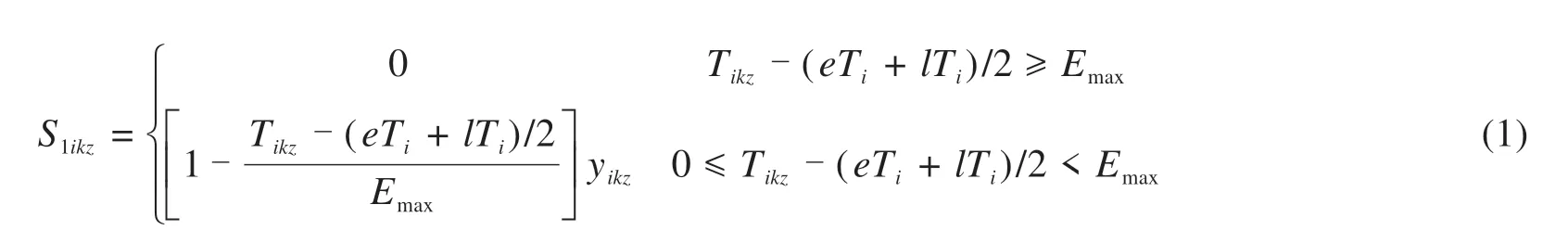
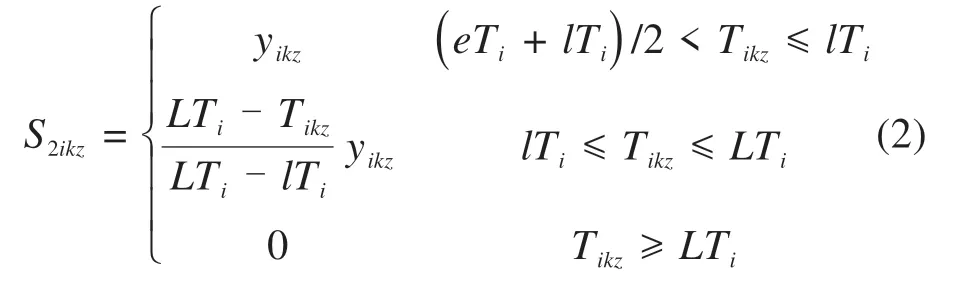
若车辆到达需求点i时车内乘客数为ci，若服务区域内所有需求点所有乘客的平均满意度Z1根据加权平均确定，则可表示为：

运营商利润Z2为运营收益与运营成本之差，运营成本包括车辆发车及行驶成本E1(元)、车辆早到与晚到的惩罚成本E2(元)，运营收益即票价收入E3(元)，票价采用一票制。设分区z班次k的发车时间为fkz，需求点i到j的最短距离为dij，分区z班次k早到或晚到需求点i的惩罚成本为Wizk，班次总数为K，λ是票价，γ是车辆行驶距离与经济成本的转换系数，C0为发车成本，ξ1,ξ2分别为早到和晚到的惩罚成本；分区z班次k到达需求点i前途经的需求点集合PREikz，u为需求点每位乘客的上车时间；xijkz∈{0,1}，若分区z班次k途经需求点i、j之间的最短路，则为1，否则为0。则运营商利润Z2为：

式(4)右边第1～3 项分别为收益、行驶成本和发车成本之和、惩罚成本。式(5)表示，服务于需求点i的车辆在预约时间窗内到达，则早到或晚到惩罚Wizk为0，否则按与预约时间窗的时间差进行惩罚；式(6)是服务于需求点i的车辆到达需求点i的时间计算式。

设ypkz∈{0,1}，若边界上的需求点p(p∈Ip)由分区z班次k服务需求点i则为1，否则为0；yqkz∈{0,1}，若班次k服务分区z内的需求点q(q∈Iz)则为1，否则为0；Q为车辆容量，Tmax为最大行程时间。参考文献[19]，优化时选择乘客满意度和运营商利润等2 个优化指标，故多分区协调的、车辆路径与发车时间协调的多目标优化模型可表示为：

式(7)为优化目标，即同时兼顾乘客满意度、运营商利润；式(8)为车辆容量约束；式(9)表示每一个需求点只被一辆车服务；式(10)表示车辆从起点出发要返回起点；式(11)为分区z班次k从需求点i至其近邻的下游i+1的时间关联约束；式(12)为需求响应公交最大行程时间约束。

2 算法设计

多分区协调的、车辆路径与发车时间协调的多目标优化模型是在车辆路径与发车时间优化的基础上再协调分配边界上的乘客需求，模型求解的关键还是车辆路径与发车时间的多目标协调优化，因带精英策略的快速非支配排序遗传算法的非劣解在目标空间分布均匀，且收敛性和鲁棒性好，比较适合于求解车辆路径问题[20]，故本文基于带精英策略的快速非支配排序遗传算法来设计求解算法，算法流程如图2所示。

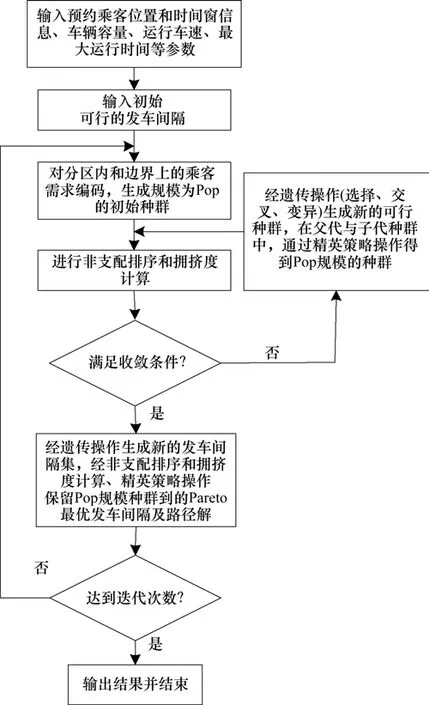
图2 算法流程图Fig.2 Algorithm flowchart

为同时优化发车时间和车辆路径，图2所示的流程是基于参考文献[13]的双遗传算法设计的，内循环是在发车时间确定的条件下进行路径优化，外循环是选择可接受的发车时间集。本文算法中，需求点和发车间隔均采用自然数编码[21]。双目标问题中，设个体i和j的目标值分别为Z1i,Z2i,Z1j和Z2j，若对任意个体j≠i，均有Z1i>Z1j且Z2i>Z2j，则个体i为非支配个体；重复比较，可得到非支配个体集，形成第1 级非支配层；忽略第1 级非支配个体，重复比较，可得到第2级非支配层；依此类推，整个种群被分层。通过精英策略操作，从当前父代和子代中挑选出Pop 规模的种群，选择时从第1 级非支配层开始、同一非支配层从拥挤度[20]最大的开始。在同一非支配层，根据每一目标函数值的升序对个体排序，设边界个体的拥挤度为∝,非边界个体i的初始拥挤度id为0，则id的迭代式为id=|Z1i+1-Z1i-1|+|Z2i+1-Z2i-1|。

3 算例分析

换乘站O 的坐标为(3.50,3.50)，预约需求情况见表1，分区情况如图1 所示。Tmax=25 min，V=30 km/h，u=6 s/人；λ=1.2 元；Q=15，C0=10 元/台，γ=1.2元/km，ξ1和ξ2分别为1.2,1.1，Emax=4 min。

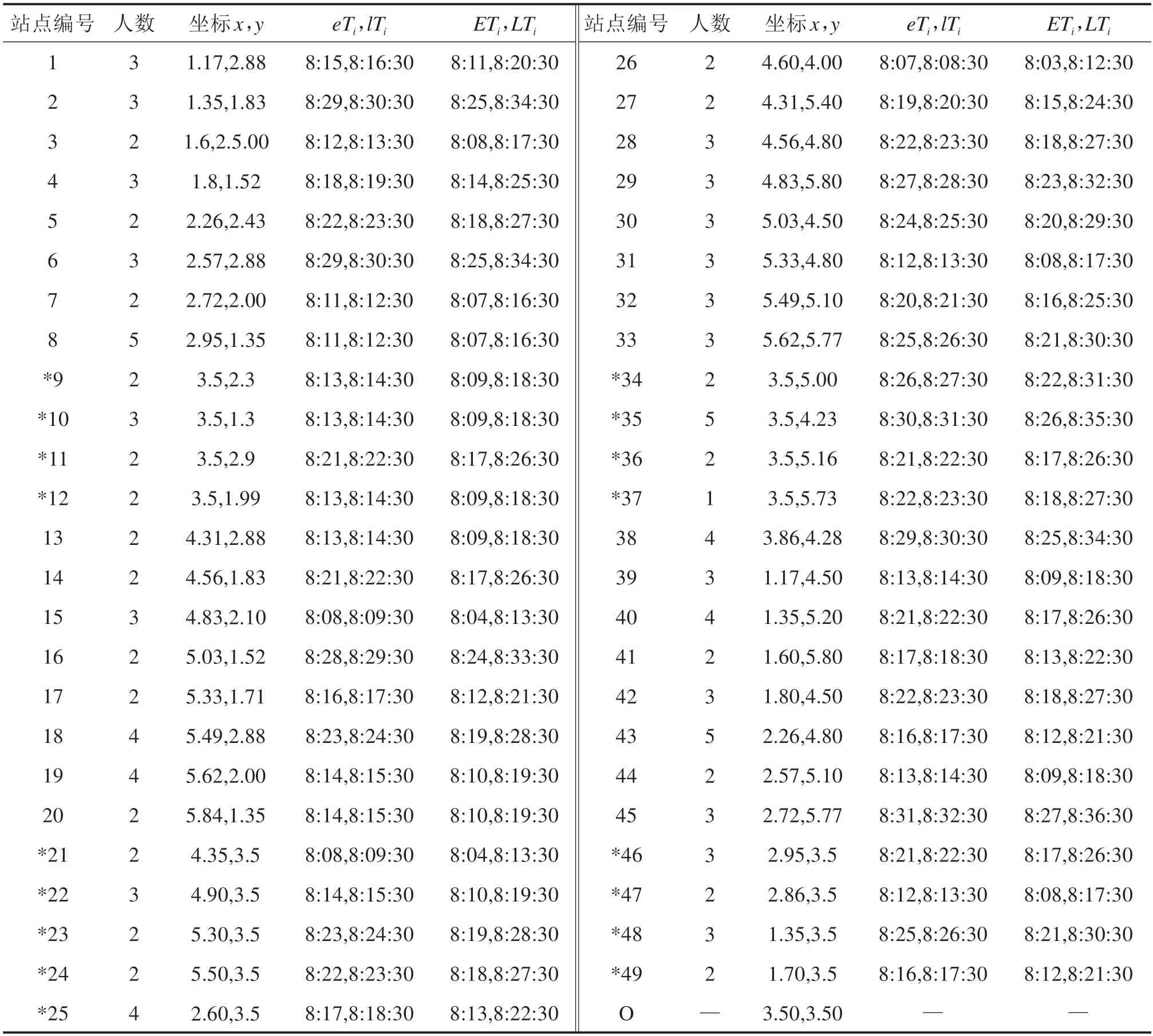
表1 乘客预约信息Table 1 Passenger reservation information

3.1 不同发车时间方案的比较

在乘客需求等一定条件下，运用本文模型获取分区协调的、发车时间和车辆路径协调的运营方案，也获取发车时间固定下分区协调的车辆路径方案(发车时间事先固定)，不同发车时间方案的计算结果及其比较如图3和表2所示。由图3可知，发车时间与路径协调优化下的Pareto解集对应的点均位于发车时间固定仅路径优化下的左下方，说明相同利润下，协调优化的满意度均高于发车时间固定的；相同满意度下，协调优化的利润均高于发车时间固定的，协调优化的效果显著。由表2可知，若追求利润最大，与发车时间固定的路径优化相比，发车时间与路径协调优化的利润和满意度分别增加了1.1%和0.01；若追求满意度最大，利润和满意度分别增加了8.4%和0.05；若获取利润与满意度均较佳的方案(对应图3 的A2 和B2)，利润和满意度分别增加了4.7%和0.07。

表2 不同发车时间方案计算结果的比较Table 2 Comparison of calculation results of different departure time schemes

图3 不同发车时间方案的Pareto解集Fig.3 Pareto solution set of different departure time schemes

3.2 边界上需求点不同分配方式的比较

在乘客需求等一定条件下，运用本文模型获取分区协调的、发车时间和车辆路径协调的运营方案，也获取边界上需求固定分配条件下的发车时间和车辆路径方案，边界上需求点不同分配方式的计算结果及其比较如图4 和表3 所示。由图4可知，边界上需求协调分配的Pareto解集对应的点均位于固定分配的Pareto解集的左下方，说明相同利润下，协调分配的满意度要明显高于固定分配的；相同满意度下，协调分配的利润要明显高于固定分配的，协调分配的效果显著。由表3 可知，若追求运营商利润最大，与固定分配相比，协调分配的利润增加了7.4%，但满意度有所降低；若追求满意度最大，利润增加了5.3%，但满意度相同；若获取利润与满意度均较佳的方案(图4 中的A2 和C2)，协调分配的利润和满意度分别增加了5.5%和0.02，说明边界上需求协调分配的利润增加较明显，但满意度变化趋势不明显。

图4 边界上需求点不同分配方式的Pareto解集Fig.4 Pareto solution set of different distribution modes of demand points on the boundary

表3 边界上需求点不同分配方式计算结果的比较Table 3 Comparison of calculation results under different allocation methods of demand points on the boundary

3.3 车辆容量的影响分析

在乘客需求等一定条件下，只改变车辆容量(车辆容量改变，其发车成本也将随之改变)，分析容量变化对运营商利润、乘客满意度、行驶总里程的影响。设定车辆基准容量为15人/车(发车成本为10元/台)，分析容量增至25人/车(发车成本为13元/台)后对优化方案的影响，计算结果分别见表4和图5。

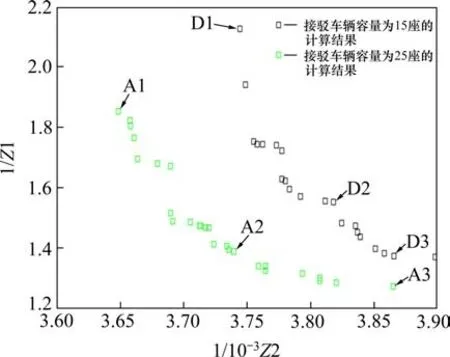
图5 接驳车容量变化下的Pareto解集Fig.5 Pareto solution set under the change of feeder capacity

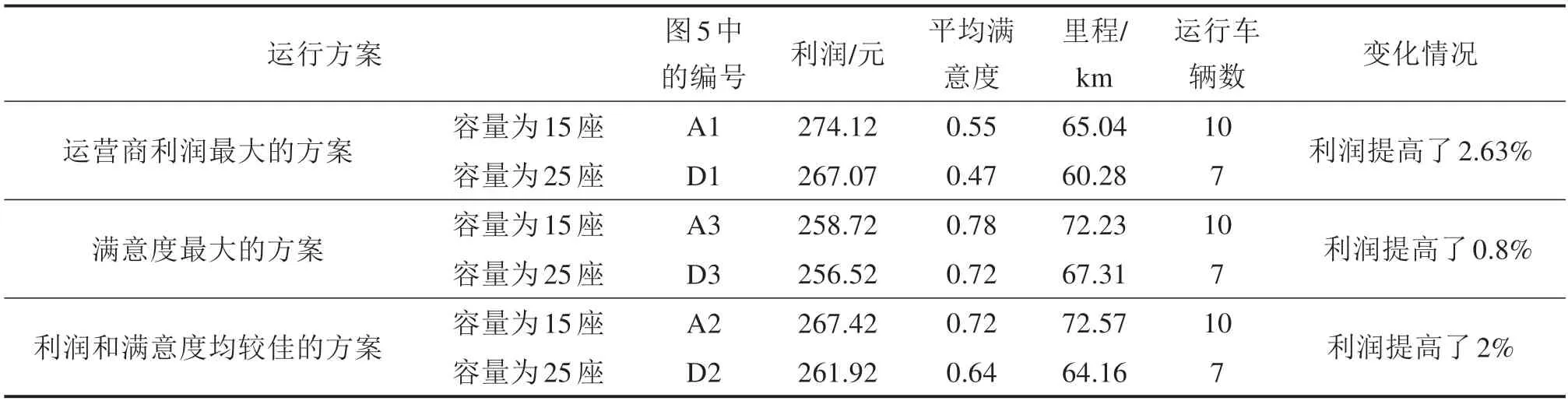
表4 车辆容量变化下计算结果的比较Table 4 Comparison of calculated results between vehicle capacity changes

由图5可知，容量15座下的Pareto解集对应的点均位于容量25座下的左下方，说明相同利润下，15座的满意度要明显高于25座的；相同满意度下，15 座的利润要明显高，15 座的更适合当前条件下的接驳服务。由表4可知，若追求利润最大，与25座的相比，容量15 座接驳车的利润和满意度分别增加了2.63%，0.08；若追求满意度最大，利润和满意度分别增加了0.8%，0.06；若获取利润与满意度均较佳的方案(对应图5 中的A2 和D2)，利润和满意度分别增加了2%，0.08，说明车辆容量的大小会显著影响系统性能。

4 结论

1) 兼顾运营商利润和乘客满意度，构建了边界上需求点协调分配的、发车时间和车辆路径协调的多目标优化模型及其带精英策略的快速非支配排序遗传算法。

2) 算例结果表明，发车时间方案、边界上需求的分配方式、车辆容量对多分区RFT 系统的多目标协调有显著影响。相同利润下，发车时间与路径协调优化的满意度均高于发车时间固定仅路径优化的；与边界上需求的固定分配相比，边界上需求的协调分配能获得更高的满意度；相同满意度下也类似。考虑车辆容量对利润和满意度的影响，接驳区域内一定需求量下应有最适宜的接驳车辆容量，宜配备合适的车型。

3) 进一步研究工作是分区范围与数量、车辆路径与调度的多目标协调优化。