基于一维卷积神经网络的恒星光谱分类研究

艾霖嫔,杨锦涛,徐权峰,张静敏,杜利婷,周卫红,2

(1.云南民族大学 数学与计算机科学学院,云南 昆明 650500; 2.中国科学院 天体结构与演化重点实验室,云南 昆明 650011)

研究天体光谱能发现许多对天文研究有重要的意义的信息,其中天体光谱的分类研究是天体光谱研究的重要一环.但目前仍有大量的天体没有经过光谱观测，郭守敬望远镜(LAMOST)有着极高的光谱获取率,为我国天文学研究做出了重大贡献.如今LAMOST光谱发布已进入千万量级时代,创下多项世界之最.

对于天体光谱的分类研究学者们进行了许多的尝试.覃冬梅等[1]利用主分量分析法来研究恒星光谱的分类,该方法的实验结果跟基南系统的恒星分类标准相差无几,表明了该方法的有效性;张华煜[2]提出的分类模型是基于支持向量机的层次型聚类多类分类器,该模型可以有效提高分类速度;康超[3]针对M矮星的分类研究，提出残差分布度量的方法,证实了该方法对天体光谱进行分类的可行性;赵旭俊等[4]提出利用分类模式树提取恒星光谱中属性的出现频率,挖掘分类的规则,表明了该方法对恒星光谱分类有较高的准确率;刘忠宝等[5]为了解决数据样本很大时,支持向量机计算量大速度慢等问题,提出流形模糊双支持向量机应用于SDSS的恒星光谱数据集,该方法不仅大幅度减少了计算的时间,同时还能有效降低噪声点以及奇异点的影响,提高分类精度.

随着LAMOST、SDSS等巡天项目的开展,光谱数据量呈爆炸式的增长,我们必须寻求快速、高效、精确的分类方法来对天体光谱进行分类.由于深度学习在图像识别领域取得了非凡的成就,学者们也开始将深度学习应用到天体光谱分类领域.石超君等[6]提出基于卷积神经网络对K型和F型恒星光谱进行分类,结果表明卷积神经网络能对K型和F型恒星光谱快速的分类筛选,训练的数据量与模型泛化能力,分类准确率成正比;张静敏等[7]提出基于深度信念网络的LAMOST恒星光谱分类研究方法,验证了该模型对F、G、K这3种恒星光谱分类的有效性;王奇勋等[8]针对LAMOST光谱数据优化了DenseNet网络,对恒星、星系和类星体3类天体光谱进行分类,该优化后的模型具有可解释性强、鲁棒性强、泛化能力强等优点, 可用于天体光谱的分类研究;许婷婷等[9]利用DBN模型对光谱数据特征的分层学习具有数据降维的特点,基于深度学习训练了一个深度信念网络对F、G和K 3种恒星光谱进行分类,没有对天体光谱进行降维处理,直接训练DBN模型,最终准确率为0.9303.张静敏等[10]又提出1种基于2维傅里叶谱图像的特征提取方法,采用短时傅里叶变换将1维光谱数据变换成2维傅里叶谱图像,再利用深度卷积网络模型对得到的2维傅里叶谱图像进行分类,最终的分类准确率是0.929 0.

1 恒星光谱数据

恒星光谱分类方法有西奇分类、哈佛系统、威尔逊山系统、基南系统等,其中基南系统对于恒星光谱的分类得到了广泛的应用.它按照恒星的表面温度从高到低对恒星光谱进行分类,仍然使用哈佛系统对光谱分类的标示,将恒星的光谱分成O、B、A、F、G、K、M 7大类.目前国际上的巡天项目有LAMOST、斯隆数字巡天(Sloan Digital Sky Survey，缩写为SDSS)等,而LAMOST获取到的光谱是所有天文望远镜中最多的,历经5年,在LAMOST全体工作人员的共同努力下，LAMOST一期光谱巡天任务圆满完成,LAMOST DR5数据集也于2017年12月31日正式发布,共发布了901万条光谱,信噪比大于10,其中高质量光谱数达到了777万条.

在LAMOST中，天体光谱存储形式为FITS格式，其包含许多恒星的属性特征信息，而这些信息在某一具体问题中不一定都能用，因而在恒星光谱分类中选取其中的一个数字矩阵中的流量与波长构成光谱图，横坐标为波长，纵坐标为流量.不同类别的恒星光谱,其流量、形状、峰宽有一定的差异,即使同一波长处的流量也相差很多,不同的恒星光谱波长不同时流量也不同.根据这些特性,我们可以判断出恒星光谱的类型.由于不同类型的恒星光谱在不同的波长处具有各自的发射线与吸收线,从而不同类型的恒星光谱的光谱图会有很大的差异,因此可以将恒星光谱看成是一维信号,再利用一维卷积神经网络中一维卷积计算的特性，实现了对一维恒星光谱的自动分类[11].

2 一维卷积神经网络

在20世纪80年代就有学者开始研究卷积神经网络,此后深度学习的理论日趋成熟,以及计算机被日益改进,卷积神经网络也快速的发展.

卷积神经网络是1种前馈网络,是深度学习领域比较典型的算法.卷积神经网络的特征学习能力可以有效的学习数据中的特征,并学会怎样提取特征.卷积神经网络被广泛应用于分类识别研究,其中一维卷积神经网络对于时间序列、电信号以及音频信号等领域的分析有着出色的表现,鉴于此将一维卷积神经网络应用于天体光谱分类的研究.

2.1 一维卷积运算

卷积是表征函数f(x)或g(x)先进行翻转,另一个表征函数进行平移,它们重合部分函数值乘积对重合区间长度的积分,即“循环乘积与加和”一维卷积的数学定义公式如下：

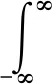
(1)

图1 一维卷积运算过程

2.2 一维卷积神经网络结构

卷积神经网络一般结构包括：

1) 输入层:通常一维卷积神经网络处理的数组类型是一维或二维的,在原始数据进入输入层之前会对其进行归一化处理;

2) 卷积层:提取输入数据的局部特征,提取到的特征进入池化层继续筛选和过滤;

3) 池化层:首要的作用是降采样,过滤掉对分类识别影响不大的特征,将数据压缩,完成特征的降维处理,可实现参数数量的减少,提升网络模型的计算速度,同时提高模型的容错性,最终获得更有代表性的特征;

4) 全连接层:输入数据经过卷积层,池化层的处理,得到极具代表性的抽象化特征,由全连接层整合起来;

5) 输出层:给出模型的预测结果,此次分类任务完成.

图2 卷积神经网络一般结构

图3 卷积神经网络分类简图

3 数据预处理及实验设计

3.1 数据的预处理

由于F、G、K 型恒星光谱由于温度相近、谱线相似导致分类准确率较低,所以文中选取 LAMOST DR5 中的F、G、K 型恒星光谱各 10 000 条,共 30 000 条,采用一维卷积神经网络模型对其进行分类,以提升这三类恒星光谱的分类精确率,其中训练数据集为 27 000 条, 测试数据集为 3 000 条,每条光谱数据的波长范围是370～910 nm.

为了后续实验方便,将用于实验的光谱数据调整为相同的维度,3 909 维.其次光谱原始数据在波长不同时流量会有很大的差异,对数据进行了归一化处理,使流量值处于同一数量级,这个操作可加快网络模型的收敛性,有利于数据分析.

图4 原始F5型、G5型、K5型光谱数据

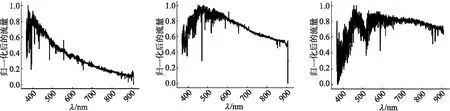
图5 归一化后的F5型、G5型、K5型光谱数据

文中使用min-max归一化, 对原数据进行了等比例缩放, 公式如下：

(2)

其中xnorm表示归一化后的数据，x为原始的光谱数据,xmax表示每条原始光谱数据的最大流量值,xmin表示每条原始光谱数据的最小流量.

3.2 实验设计

文中的一维卷积神经网络的结构包括1个输入层,7个卷积层和池化层,1个Dropout层,2个Dense层,1个输出层.其中卷积的步长设置为1,每层滤波器的大小都设置为3,滤波器的个数每层依次递增10，即第1层卷积滤波器的个数为10,到第7层滤波器的个数为70, 本实验在每一层卷积层的后面都添加了池化层,采用的是最大池化,窗口为 1×2, 网络结构如图6所示.

图6 一维卷积网络结构

为解决深层神经网络的梯度爆炸和梯度消失问题,减少输出的复杂度和防止数据的过拟合,在卷积之后使用修正线性单元ReLU函数,其函数如下：

ReLU(x)=max(0,x)

(3)

其中x为神经元的输入,当x>0时,梯度为1,解决了梯度消失的问题,加快收敛速度的同时增大了网络的鲁棒性;当x<0 时,该层的输出为0,当训练结束时真正对分类效果有影响的神经元越少网络的稀疏性越大,提取到的特征对于分类效果的影响就越强,优化了计算的过程使得网络模型的计算代价大大降低.

本实验在全连接层中加入了Dropout层,目的是防止出现过拟合,减少计算时间.交叉验证表明,Dropout率为0.5的时候,能随机生成最多的网络结构,网络模型效果最佳[12].

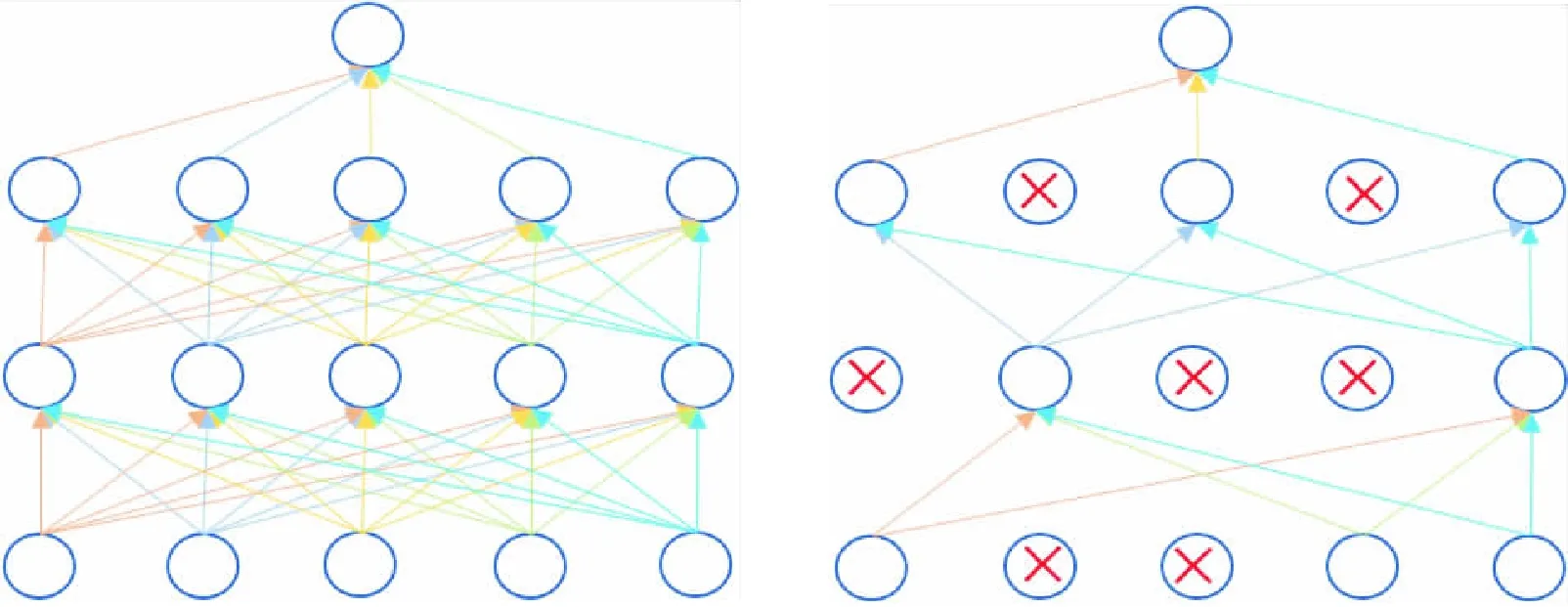
图7 标准神经网络、应用Dropout层后的神经网络

按照Dropout率随机令一定比例的神经元暂时等于零,这样能实现神经元的总个数不会减少的同时,增加网络的鲁棒性.参数被传递到下一次迭代中,进行新一轮的随机丢弃,一直到训练完成为止.

4 实验结果与分析

将 3 000 条测试数据,用于训练好的一维卷积神经网络模型进行测试,得到F型、G型、K型光谱在测试集上的混淆矩阵.可以看出在对F型光谱进行分类预测时,有5条被分类为G型光谱,有一条被分类为K型光谱; 在对G型光谱进行分类预测时,有10条被分类为F型光谱,有2条被分类为K型光谱; 在对K型光谱进行分类预测时,没有光谱被分类为F型光谱,有35条被分类为G型光谱.在这3类恒星光谱中F型光谱和G型光谱相似性更高,混淆矩阵如表1：

表1 混淆矩阵

根据混淆矩阵可得到F型、G型、K型光谱的分类精确率、准确率、召回率以及F1分数,如表2所示：

表2 各类分类效果及平均分类效果

由表2可以看出一维卷积神经网络对恒星光谱进行分类预测时有着极强的泛化能力和鲁棒性，平均分类精确率为 0.982 2,准确率为 0.988 2,召回率为 0.982 4,F1分数为 0.982 1.其中F型恒星光谱特征最明显分类效果最好,精确率、准确率、召回率以及F1分数都在0.99以上.

鉴于本文使用的数据集来源以及实验数据大小与文献[9]～[10]相同,将本文方法所获得的结果与DBN和Inception v3方法获得的结果做对比,如表3所示：

表3 DBN、Inception v3与本文使用方法的对比

由表3可以看出,采用3种不同的方法对恒星光谱进行分类研究,本文使用的方法效果更好,花费时间更少.表明了一维卷积神经网络对于恒星光谱分类的泛化能力强,分类准确率高,计算成本更小. DBN、Inception v3方法对于恒星光谱的分类可能存在以下问题:

1) 许婷婷等[9]利用DBN模型对光谱数据特征的分层学习具有数据降维的特点,基于深度学习训练了一个深度信念网络对F、G和K 3种恒星光谱进行分类,没有对恒星光谱进行降维处理,直接训练DBN模型.但该分类模型可能不能很好的找出数据的联合概率分布, 未能获取潜藏在数据中的高层信息导致分类精度不高,且该模型的时间复杂度明显增加.

2) 张静敏等[10]采用短时傅里叶变换将1维光谱数据变换成2维傅里叶谱图像,再利用Inception v3网络模型对得到的2维傅里叶谱图像进行分类.但将1维光谱数据变换成2维傅里叶谱图像的过程中可能造成原始光谱特征信息的丢失;其次新生成的2维傅里叶谱图像特征分布并不明显,深度卷积网络模型可能不能很好的对新生成的图像进行分类;最后将1维光谱数据变换成2维傅里叶谱图像,导致分类模型的时间复杂度也明显增加.

本文鉴于一维卷积神经网络可以很好地分析具有固定长度周期的信号数据,将其应用于F5、G5、K5型恒星光谱的分类研究,通过实验可以看出:

1) 一维卷积神经网络有很强的泛化能力以及鲁棒性,能有效应用于恒星光谱的分类研究中;

2) 一维卷积神经网络用于恒星光谱的分类研究能有效降低计算代价;

3) 直接对光谱数据进行一维卷积处理,有效降低了将光谱数据进行变换处理,再应用于传统二维卷积神经网络的特征损失,进而提高分类准确率.

5 结语

为了提高F、G、K型恒星光谱的分类可信度,本文将一维卷积神经网络应用于这3种恒星光谱的分类识别研究中,平均精确率达到 0.982 2,平均准确率达到 0.988 2,平均召回率达到 0.982 4,平均F1分数达到 0.982 1,相对于其他的方法有了较大的提升.表明了一维卷积神经网络模型对于恒星光谱数据分类具有很强的泛化能力.将本文方法与DBN以及Inception v3方法的实验结果对比发现一维卷积神经网络模型对恒星光谱分类的效果更好.但用于实验的数据量较少,在接下来的工作中,会选取更多的光谱数据来进行实验,与本文实验以及其他方法进行对比分析,希望进一步提高F、G、K型恒星光谱的分类可信度.并且也会继续将一维卷积神经网络应用于分类精度较低的光谱，以验证一维卷积神经网络对于低精度恒星光谱分类的有效性,为人类探索宇宙的奥秘尽一份绵薄之力.