近距离爆炸荷载作用下H型钢柱毁伤数值分析*

李鹏鹏，高振儒，陈叶青，武双章，周兆鹏

(1.陆军工程大学 野战工程学院，南京 210007；2.军事科学院 国防工程研究院，北京 100036)

战争状态下，跟战争紧密相关的工业厂房是敌方重点打击目标。钢结构厂房具有抗震、抗风、耐久、环保等特点，逐渐取代传统的钢筋混泥土结构厂房，成为工业厂房的主要构筑形式。H型钢柱，因其强度高，自重轻，被广泛用作钢结构厂房承重柱。航空爆破炸弹，因其强大的摧毁能力，非常适合用作攻击厂房，现代高技术战争中，对地面目标实施空中打击已成为战争的首选方案。航空爆破炸弹，壳体一般用普通钢材制成，装药通常为TNT炸药，弹体壁厚与半径之比小于0.1，对厂房造成的破坏以装药爆炸冲击荷载为主。给航空爆破炸弹加装激光、电视、红外、毫米波等制导装置，能有效提升航空爆破炸弹的命中精度，对厂房实施接触爆炸毁伤或近距离爆炸毁伤。H型钢柱作为多数钢结构厂房的重要承重及传力构件，一旦被爆炸袭击失去承载能力，很可能造成连锁反应，导致整个厂房失稳，甚至倒塌。因此，研究H型钢柱在爆炸荷载作用下的毁伤机理具有十分重要的现实需求和科学意义。

Mohammad Ali Hadianfard等使用可靠性理论并考虑到爆炸荷载和材料特性的不确定性[1,2]，改进了一种确定爆炸荷载作用下钢柱损伤概率的方法。Nassr等基于SDOF近似值模型[3]，研究了爆炸荷载作用下梁柱的强度和稳定性。周龙云等研究了H型钢柱在爆炸荷载作用下的剩余承载力系数K与相对挠度ωR的关系[4]，提出了钢柱受损的判定依据并划分了受损钢柱的损伤等级。周游等将薄壁方管置于单次和重复爆炸场中进行冲击实验，获得了爆炸次数对方管动力响应的影响规律[5]。张亚东等通过有限元程序ABAQUS对完好钢柱的动力响应进行数值模拟，研究了试件垮塌前后所产生的塑性铰的变化与移动规律[6]。高金明等应用新型CONWEP爆炸加载方式，分析不同爆炸距离下变截面H型钢的动态响应过程[7]，得到了构件变形的响应规律。张新鑫等采用LS-DYNA软件对不同比例距离爆炸荷载作用下H型钢梁的动态响应进行了数值分析[8]，发现随着比例距离的减小，梁由弹性变形阶段转变为塑性变形阶段。

从国内外相关资料来看，目前爆炸荷载作用下钢柱毁伤的研究，大多是都是针对中远距离爆炸荷载作用下的研究，而对近距离爆炸荷载的关注较少。基于显式有限元方法软件LS-DYNA，区分不同比例距离，研究了近距离爆炸荷载作用前后钢柱的轴向承载能力的变化，计算了损伤指数。H型钢柱的毁伤分析，对于钢结构厂房的设计与防护，武器弹药的效能评估等具有重要的意义。

1 爆源与H型钢承重柱

1.1 爆源

爆源为航空爆破炸弹，圆径一般在100 kg级以上，最大可达20 000 kg级，其中以250～500 kg级使用最为广泛。高阻外形的航空炸弹长细比较小，低阻外形的航空炸弹长细比较大[9]。本研究选取某型高阻外形航空爆破炸弹作为模型，炸弹圆径250 kg，装填系数0.4，装药TNT当量C1=100 kg，装药形状为圆柱形，装药长细比为1.0，忽略弹壁厚度，装药直径d1=427 mm，装药高度h1=427 mm。

图 1 典型爆炸冲击波压力时程曲线Fig. 1 Typical explosion shock wave pressure time history curve

(1)

球形装药情形中爆炸产物所占据体积的极限半径大约是其初始半径的10～12倍，圆柱形装药时则约为30～40倍。本文所采用的爆源虽为圆柱形装药，但由于其装药直径等于装药高度，故其爆炸产物所占据的极限半径应介于球形装药和圆柱形装药之间。所以近距离爆炸时，爆炸产物的作用不容忽视。

1.2 H型钢承重柱

参考某钢结构厂房，结构横向尺寸为48 m，两跨跨度均为24 m，每跨承载40 t吊车，参考图2(a)；结构纵向尺寸为96 m，采用等柱距，柱距为8 m，参考图2(b)。

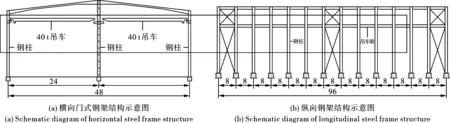
图 2 某钢结构厂房示意图(单位：m)Fig. 2 Schematic diagram of a steel structure workshop(unit:m)

钢柱为等截面Q355B热轧H型钢柱，钢柱高H1=1250 cm，截面(mm)(H750 ×375× 25×35)，屈服强度σ=355 MPa，弹性模量E=2.06×105MPa。x方向的截面惯性矩Ix1=4.013×105cm4，y方向的截面惯性矩Iy1=3.085×104cm4；x方向的截面抵抗矩和净截面抵抗矩Wx1=Wnx1=1.070×104cm3，y方向的截面抵抗矩和净截面抵抗矩Wy1=Wny1=1.645×103cm3，x方向的回转半径ix1=30.450 cm，y方向的回转半径iy1=8.440 cm；横截面面积S1=432.500 cm2，如图3所示。

图 3 H型钢柱示意图Fig. 3 Schematic diagram of H-shaped steel column

2 建立爆炸毁伤有限元模型

2.1 近距离无限空中爆炸判别条件

炸弹装药中心与H型钢柱翼缘中心处于同一水平位置，装药轴对称中心线与H型钢柱高度方向平行，装药中心距离地面的高度H=6.250 m，装药的比例高度

(2)

符合装药无限空中爆炸时装药的比例高度，可以认为炸弹是在无限空中爆炸。

2.2 相似转换

根据相似法则对实际模型作相似转换，相似倍数取0.2，即相似转换后的炸弹尺寸、H型钢柱尺寸及相互间的几何关系等较原型尺寸均缩小0.2倍。近距离爆炸时，对目标的破坏作用取决于冲击波的冲量，两组模型i1/r1=i2/r2。

式中：i1为实际模型爆炸冲击波冲量；i2为相似模型爆炸冲击波冲量；r1为实际模型H型钢柱翼缘厚度；r2为相似模型H型钢柱翼缘厚度。

作相似变换后，装药直径d2=8.54 cm，高度h2=8.54 cm，TNT当量C2=800.00 g；钢柱高H2=250.00 cm，截面(mm)(H150 ×75× 5×7)，x方向的截面惯性矩为Ix2=642.02 cm4，y方向的截面惯性矩为Iy2=49.36 cm4；x方向的截面抵抗矩和净截面抵抗矩Wx2=Wnx2=85.60 cm3，y方向的截面抵抗矩和净截面抵抗矩Wy2=Wny2=13.16 cm3；x方向的回转半径ix2= 6.09 cm，y方向的回转半径iy2=1.68 cm；横截面面积S2=17.30 cm2。

2.3 有限元模型

整体模型由空气、装药、H型钢柱、上下刚性面板5部分组成，假设空气为理想气体，采用NULL材料模型，状态方程用LINEAR_POLYNOMIAL表示；装药采用 HIGH_EXPLOSIVE_BURN 材料模型，状态方程用JWL表示；H型钢柱采用PLASTIC_KINEMATIC模型，该材料模型适合于模拟各向同性和运动硬化塑性，并且可以选择包括速率效应[11]。

有限元模型采用流固耦合方式模拟空气、装药与H型钢柱之间的相互作用，装药与空气之间采用多物质耦合，无反射边界来模拟无限空气域，腹板、翼缘连接处采用共节点的方式模拟热轧，H型钢柱与上下刚性面板共节点连接，下刚性面板无平动与转动自由度，上刚性面板只有沿面板法向法向的自由度，如图4所示。

图 4 有限元模型Fig. 4 Finite element

2.4 材料本构模型及状态方程

(1)空气材料模型及状态方程

采用LS-DYNA材料库中的9号*MAT_NULL模型来模拟空气域，空气材料模型具体参数的取值如表1所示[12]。

表1 空气MAT_NULL模型Table 1 Air MAT_NULL model

空气材料*EOS_LINEAR_POLYNOMIAL状态方程如表2所示。

表2 空气EOS_LINEAR_POLYNOMIAL状态方程Table 2 Air EOS_LINEAR_POLYNOMIAL state equation

(2)装药材料模型及状态方程

采用LS-DYNA材料库中的8号*MAT_HIGH_EXPLOSIVE_BURN模型来模拟装药在空气中的爆轰反应[12]。装药材料模型具体参数的取值如表3所示。

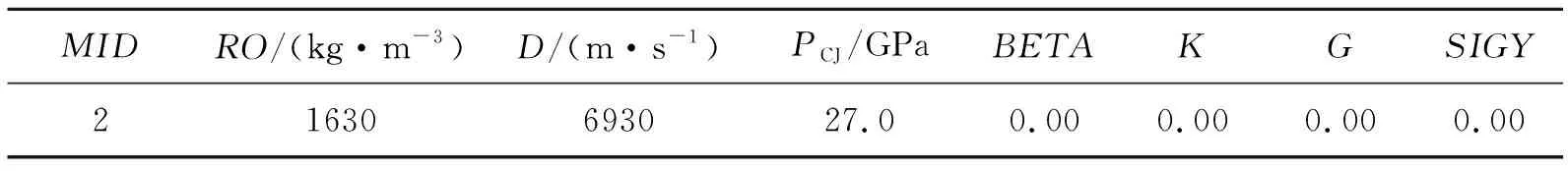
表3 装药MAT_HIGH_EXPLOSIVE_BURN模型Table 3 Explosive MAT_HIGH_EXPLOSIVE_BURN model

装药材料*EOS_JWL状态方程如表4所示。

表4 装药EOS_JWL状态方程Table 4 Explosive EOS_JWL state equation

(3)钢材本构模型

选用LS-DYNA材料库中的MAT_PLASTIC_KINEMATIC模型[13,14]，具体参数的取值如表5所示。

表5 钢材本构模型Table 5 Steel constitutive model

3 数值模拟及分析

3.1 未施加爆炸荷载作用下钢柱轴向承载能力数值模拟

钢柱轴向极限承载能力FN,max1的理论计算值

FN,max1=S2·σ=614.15 kN

(3)

极限受压状态下钢柱轴向收缩量Δl

Δl=FN,max1H2/ES2=0.43 cm

(4)

钢柱应变ε

ε=Δl/H2=1.72×10-3

(5)

研究表明，应变速率10-4s-1～10-2s-1时，金属的力学性能未发生明显变化，可按静载荷处理。

取应变速率

ε/t1=7.4910-3s-1

(6)

加载时间

t1=230.00 ms

(7)

荷载增加速率

v1=FN,max1/t1=2.67 kN/ms

(8)

数值模拟中，以2.67 kN/ms荷载增加速率加载，t2=231.00 ms，即轴向荷载FN,max 2=616.00 kN时，钢柱轴向承载能力失效。钢柱轴向极限承载能力，理论计算值FN,max 1和数值模拟值FN,max 2差值为0.30%，模型选取合理。轴向荷载与轴向位移同加载时间关系如图5所示。

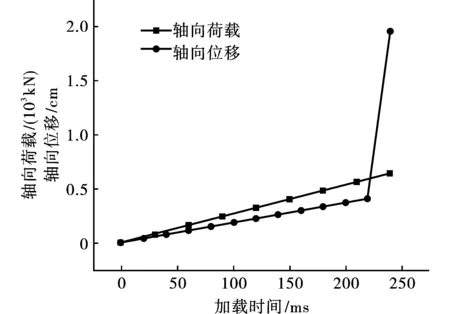
图 5 轴向荷载与位移同加载时间关系Fig. 5 The relationship between axial load and displacement with loading time

3.2 爆炸荷载作用下钢柱轴向承载能力数值模拟

第一步，使用时间的斜坡函数，将轴向荷载以2.67 kN/ms均匀增加的压力施加到安装在钢柱顶部的刚性板上，46 ms时刻加载轴向极限承载力的20%，即122.83 kN。

(9)

因

Wy2/Wx2=Wny2/Wnx2=0.15

(10)

爆炸荷载冲击后的H型钢柱，在轴向逐渐增加的荷载作用下，最终将沿腹板法向方向发生弯曲变形。爆炸荷载对钢柱造成了翼缘面法向方向的振动，腹板法向方向只发生轻微振动，综合爆炸荷载正压时间和腹板的振动情况，46～60 ms，轴向荷载不变。

第三步继续以2.67 kN/ms的荷载增加速率施加轴向荷载，直至钢柱失效，在此阶段施加到钢柱的最大荷载可认为爆炸荷载作用后钢柱的残余承载力。轴向加载如图6所示。

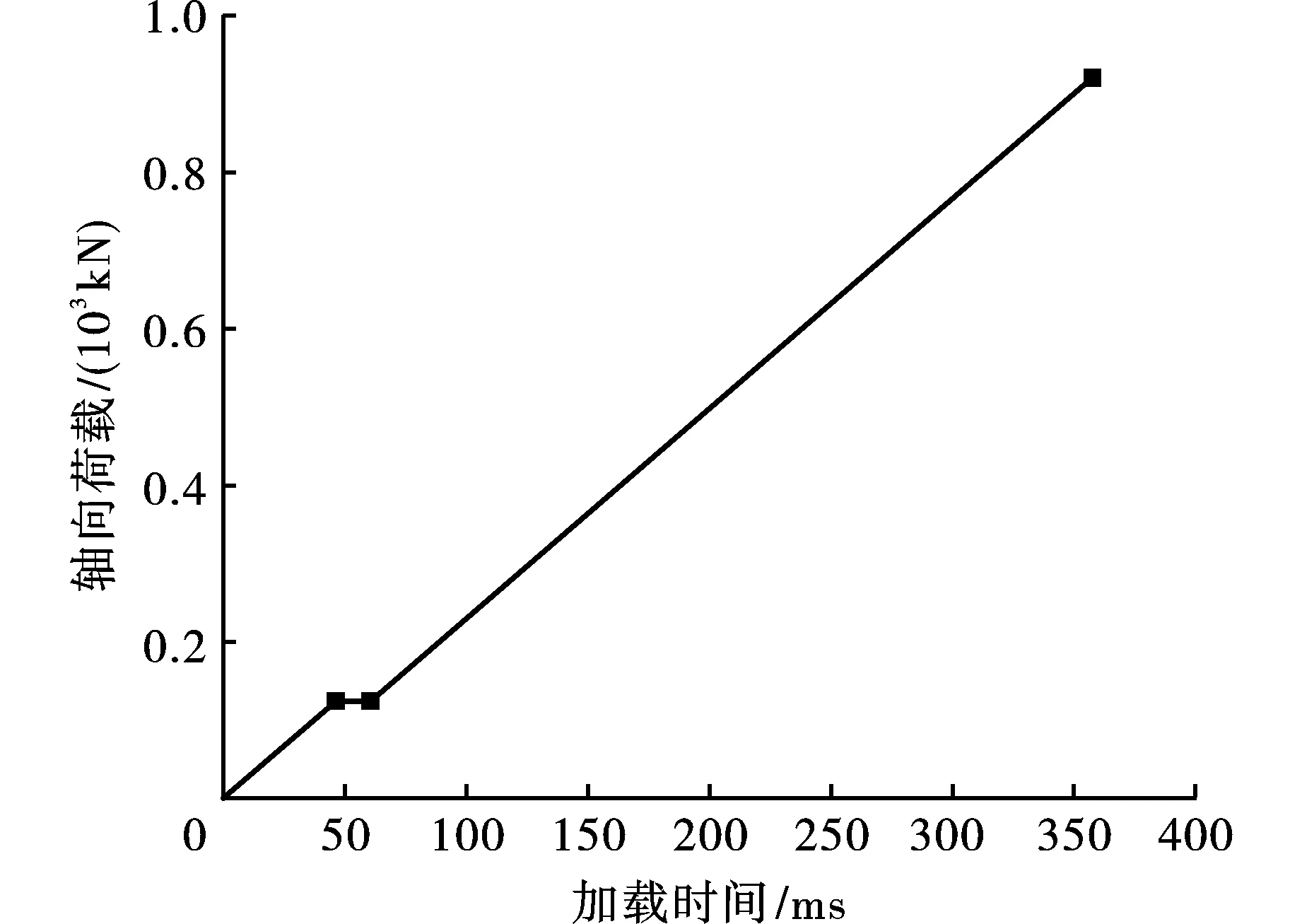
图 6 轴向加载Fig. 6 Axial loading

3.3 损伤指数

比例距离分别取：0.100,0.125,0.150,0.175,0.200,0.250,0.300,0.350,0.400(m·kg-1/3)，共9种情况，不同比例距离爆炸荷载作用下钢柱轴向承载能力持续时间如图7所示。

图 7 不同比例距离爆炸荷载作用下钢柱轴向承载能力持续时间Fig. 7 Duration of axial bearing capacity of steel column under blast load with different scaled distances

基于钢柱残余轴向承载能力，确定钢柱在爆炸荷载作用下的损伤指数(D)，可以定义如下

D=1-PResidual/PInitial

(11)

式中:PResidual为遭受爆炸冲击荷载后钢柱的残余轴向承载力；PInitial为钢柱初始极限轴向承载力。

近距离爆炸荷载作用下钢柱轴向承载能力损伤指数如图8所示，(0.100 m·kg-1/3,0.400 m·kg-1/3)区间内，损伤指数随比例距离的增加总体呈逐渐减小趋势，最大损伤指数0.533，最小损伤指数0.095；( 0.125 m·kg-1/3,0.175 m·kg-1/3)区间内，损伤指数减小速率较小；( 0.175 m·kg-1/3,0.300 m·kg-1/3)区间内，损伤指数减小速率较大；在(0.300 m·kg-1/3,0.350 m·kg-1/3)区间内，损伤指数减小速率逐渐变小；0.350 m·kg-1/3以后损伤指数减小速率趋于平缓。

根据爆炸常识和实验测定单位面积冲量公式

i+=BC/r2

(12)

式中：i+为单位面积冲量；B=250。

随着比例距离的增大，对构件造成毁伤的主要因素爆轰产物比能量和空气冲击波比冲量都会下降，所以损伤指数会逐渐减小；比例距离大于0.350 m·kg-1/3，相比于钢柱的抗冲击能力，爆轰产物比能量和空气冲击波比冲量较小，所以损伤指数较小。通过分析，比例距离0.175 m·kg-1/3是损伤指数超过0.50的临界值上限；比例距离0.350 m·kg-1/3是损伤指数低于0.10的临界值下限。但在(0.100 m·kg-1/3,0.125 m·kg-1/3)区间内，损伤指数的变化悖逆于总体趋势。见图8。

3.4 悖逆趋势分析

比例距离0.100 m·kg-1/3，爆炸荷载造成靠近装药一侧的翼缘剪切破坏，腹板30%左右剪切破坏、大部分轻微弯曲，远离装药一侧的翼缘未有明显变形，如图9(a)所示；比例距离0.125 m·kg-1/3，爆炸荷载造成靠近装药一侧的翼缘剪切破坏，腹板20%左右剪切破坏、大部分严重弯曲破坏，远离装药一侧的翼缘未有明显变形，如图9(b)所示。

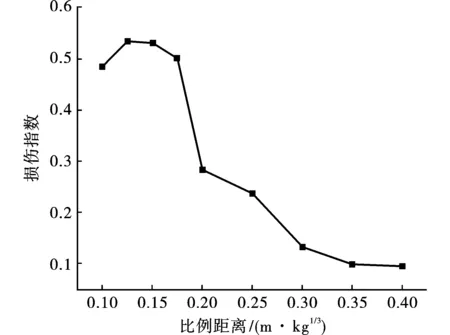
图 8 近爆作用下钢柱轴向承载能力损伤指数Fig. 8 Damage index of axial bearing capacity of steel column under close explosion

比例距离0.100 m·kg-1/3,0.125 m·kg-1/3，2种工况分别在远离装药一侧的翼缘中心位置选取1个监测点，查看所选取监测点沿翼缘法向方向位移和振幅。

初始最大位移如图10(a)所示。

S0.125 m·kg-1/3⟩S0.100 m·kg-1/3

(13)

初始振幅如图10(b)所示。

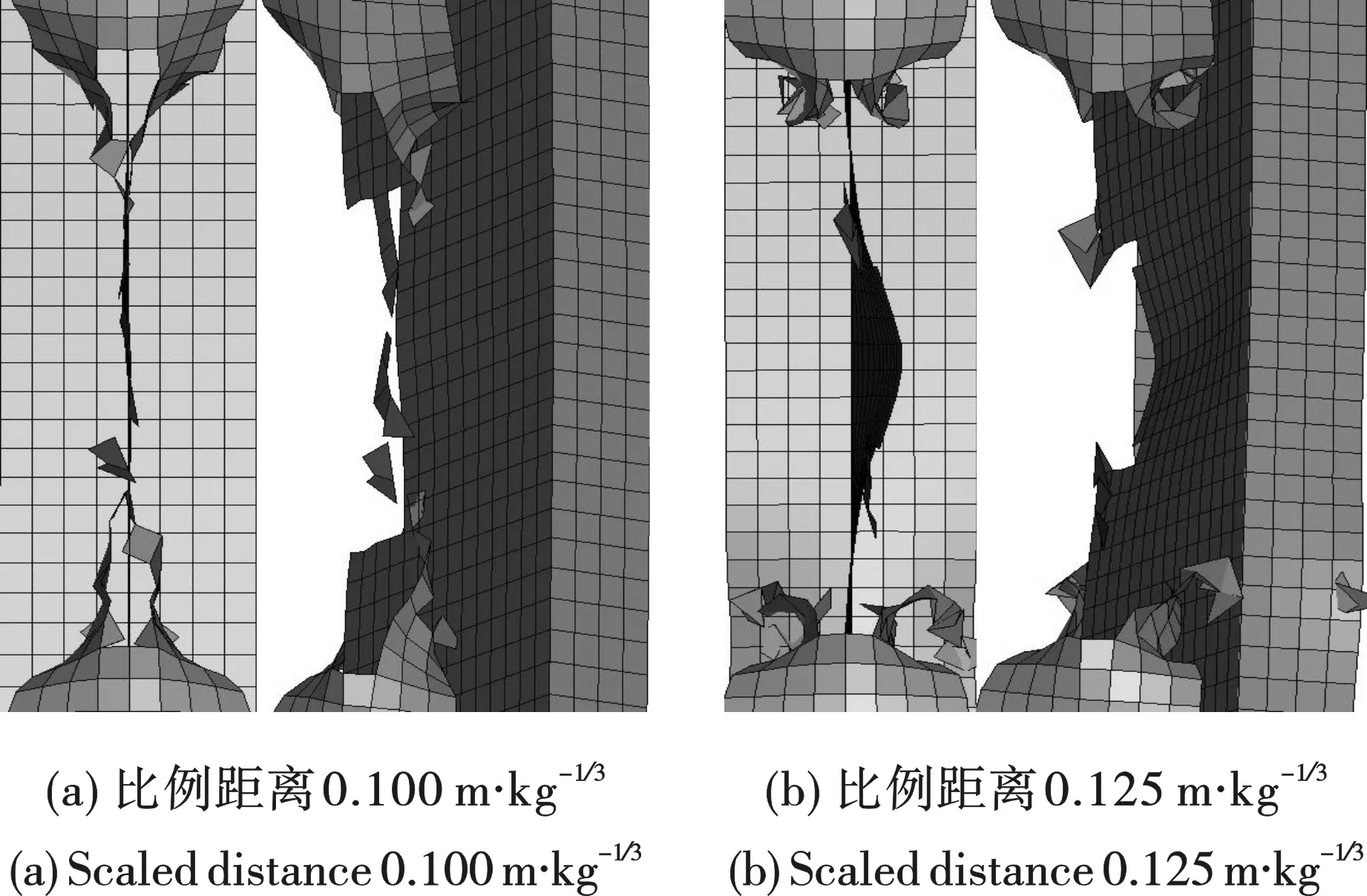
图 9 爆炸荷载对钢柱的破坏Fig. 9 Destruction of steel column by explosion load

图 10 爆炸荷载作用下远离炸药一侧的翼缘中心节点位移Fig. 10 Displacement of the center node of the flange on the side away from the explosive under explosive load

A0.100 m·kg-1/3=0.511 cm

(14)

A0.125 m·kg-1/3=0.605 cm

(15)

钢柱的自振周期T=10 ms，爆炸冲击波正压作用时间t+=0.79 ms，则

t+=T≤0.25

(16)

按照奥里所夫和萨道夫斯基研究论证，该情况下爆炸冲击波应当按照冲量计算。作为相似转换的补充，再次说明了近距离爆炸荷载作用下冲击波的破坏作用按冲量计算是可取的。

型钢的初始振动理想化为简谐振动，2种情况下钢柱被炸毁剩余部分获得的初始振动能量比

E0.100 m·kg-1/3/E0.125 m·kg-1/3=

(17)

对于一定的爆炸量，即当给出总爆炸能量时，每个组件吸收能量的增加将相应减少结构中其他组件吸收的能量[15]。比例距离0.100 m·kg-1/3与0.125 m·kg-1/3情况下，因为H型钢柱距装药中心的尺寸变化不大，可以认为两种情况下炸药爆炸传给H型钢柱的能量E是一致的。由于比例距离为0.100 m·kg-1/3时，H型钢柱的剪切破坏范围大于比例距离为0.125 m·kg-1/3时，所以对H型钢柱腹板的弯曲破坏就应小于后者。因为剪切破坏耗散的能量要远大于弯曲破坏，故两种比例距离下剪切破坏的范围差值为10%，而弯曲破坏的范围差值要大很多，且赋予后者更多的初始振动能量。这正是(0.100 m·kg-1/3,0.125 m·kg-1/3)区间内，损伤指数的变化悖逆于总体趋势的原因所在。

4 结论

通过分析，得出以下结论：

(1)近距离爆炸荷载作用下，随着弹目距离增大，钢柱损伤指数总体呈逐渐减小趋势。

(2)比例距离0.350 m·kg-1/3是损伤指数低于10%的临界值下限，比例距离超过临界值下限仅对钢柱造成轻微毁伤。

(3)比例距离0.175 m·kg-1/3是损伤指数超过50%的临界值上限，但未对钢柱造成严重毁伤。缩小比例距离，损伤指数提升有限，这种情况下H型钢柱仍能起到一定的轴向支撑作用。如进一步提升损伤指数，只能采取增加装药量、制作聚能槽、使用高级炸药等方法。

(4)比例距离小于0.125 m·kg-1/3时，损伤指数在小范围内悖逆总体趋势，合理利用该现象能有效提升钢结构的抗毁伤能力，同时也对武器弹药的毁伤评估提出了新要求。