基于Morris法的供水管网全局灵敏度分析

黄乐烽 杜坤 宋志刚 卢慢 董云程 许丁

(1.昆明理工大学建筑工程学院 昆明 650500； 2.云南省设计院集团有限公司 昆明 650000)

0 引言

供水管网模型可以模拟管网系统在一系列工况下的运行状态，是实现供水系统现代化管理的重要工具。当在管网模型基础上进行分析和设计时，比如模型校核、管径优化设计以及监测点布置等，模型输出结果存在不确定性，可能影响决策的有效性，部分原因是输入参数的不确定性。不确定的输入参数包括节点流量、管道阻力系数以及阀门状态等。对大型供水管网进行分析时，众多的参数意味着高维的输入空间，对问题的求解需要大量计算资源。已有研究表明[1-2]，管网模型分析结果主要受部分关键参数的影响。因此，通过灵敏度分析辨别关键参数，重点围绕关键参数进行分析，可有效降低问题复杂性和减少工作量。

灵敏度分析定性或定量评估输入参数的不确定性对模型输出结果的影响，可辅助基于模型进行的分析和设计。灵敏度分析包括局部灵敏度分析(LSA)和全局灵敏度分析(GSA)。LSA可以分析参数变化对模型输出的局部影响，在供水管网研究领域应用较多。BUSH C A等[3]通过求导法计算参数灵敏度矩阵，用于优化管网水压监测点布置。吴双利等[4]利用有限差分法研究管道摩阻变化对水压的影响，只对关键管道进行校核。与LSA相比，GSA是在整个参数定义域内，评估输入参数单独作用及交互作用对模型输出的影响，更适用于非线性的管网模型。全局灵敏度分析方法主要有多元回归法、Morris法、傅里叶幅度灵敏度检验法、Sobol’法等[5]。其中的 Sobol’法近年开始应用于供水管网领域。信昆仑等[6]利用Sobol’法对管网模型中的管道摩阻进行灵敏度分析，选取灵敏度较大的管道进行校核，其余管道摩阻则取经验值，提高了校核效率且达到了预定的精度要求。在管网多目标优化设计方面，FU G等[1]以两个基准管网为例，利用Sobol’法筛选出对管网性能影响较大的管道，再对问题进行简化，提高了进化算法对该优化问题的求解速度。

然而，Sobol’法局限性在于计算量需求大。根据SALTELLI A等[7]的建议，Sobol’法宜在输入参数不超过20个且单次模型运行时间小于1 min时使用。当管网模型中有成百上千个参数时，使用Sobol’法分析需耗费大量的计算时间。而GSA中的Morris法能以较小的计算代价获取参数灵敏度大小的排序以及参数相互作用的定性描述，还鲜有应用于管网模型研究。

针对以上问题，本文提出采用Morris法对管网模型中参数进行全局灵敏度分析，识别关键参数，降低问题复杂性。通过纽约隧道管网案例，将Morris法和Sobol’法的灵敏度分析结果进行对比分析，验证Morris法灵敏度分析的有效性。最后，对管网模型灵敏度分析方法的选择提出建议。

1 全局灵敏度分析方法

1.1 Morris法

为高效地筛选出模型中的少数重要参数，Morris于1991年提出一种GSA方法[8]。假设模型y(X)有k个参数，对于给定输入参数X=[x1,x2,…,xk]，第i个参数的一个基本效应为：

EEi=[y(x1,…,xi+△,…,xk)-y(X)]/△

(1)

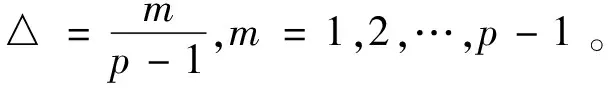
构造m×k(m=k+1)的矩阵B：

(2)

显然，将B中相邻两行作为输入参数，可计算得到k个基本效应，分别与k个参数对应。矩阵B可称为参数空间中的一条轨迹。在实际操作中，进行一随机过程，生成多条轨迹，以充分探索整个参数空间。随机过程详见参考文献[8]。按照预设轨迹数r，计算各参数基本效应的均值μi和标准差σi。μi的值越大，xi对模型输出的影响越大；而σi的值大，则说明xi对模型输出的影响是非线性的，或者xi与其他参数存在交互作用，反之亦然。

1.2 Sobol’法

Sobol’法是一种基于方差的全局灵敏度分析方法[9]，能定量评估参数对模型输出不确定性的贡献度。其核心是将目标函数的总方差分解成每个参数的方差以及参数之间相互作用的方差。

假设有k个参数的模型目标函数为：

y=f(X)=f(x1,x2,…,xk)

(3)

模型输出方差D可表示为：

(4)

式中，Di为xi单独作用造成的输出方差；Di,j是xi和xj间相互作用的方差；D1,2,…,k为k个参数间相互作用的方差。

将上式左右两边同除以D得：

(5)

式中,Si=Di/D，称为一阶灵敏度；Si,j=Di,j/D，称为二阶灵敏度；S1,2,…,k是k阶灵敏度。总灵敏度STi=∑S(i)表示xi对模型输出的总影响，其中S(i)为所有包含参数i的灵敏度。STi-Si可用于表征xi与其他输入变量之间的交互作用对模型输出的影响。

通常用Si和STi来评估参数对模型输出的影响。对于Si和STi的计算，采用Saltelli推荐的方法[10]，需运行模型N(k+2)次。此外，Sobol’方法要求样本覆盖整个参数空间，为此采用拉丁超立方抽样对参数空间进行抽样。

2 案例分析

以纽约隧道管网为例，展示Morris法和Sobol’法在管网优化设计中的应用，并从计算精度和计算量两个方面对上述两个方法进行对比分析。

2.1 纽约隧道问题

纽约隧道问题是由SCHAAKE J C等[11]于1969年提出的，其管网布局如图1所示，包含1个水源、20个节点和21个管段。为满足用户用水需求，需对该管网进行扩建，可在现存的管道旁平行敷设新管。新增管道有16种管径可选，不同的管径造价不同。管网多目标优化设计的目的是兼顾经济性和可靠性，寻求最优解决方案。对于这种优化问题，通常利用进化算法进行求解。但其高维度的参数空间对计算量的需求很大，导致算法搜索效率低下。利用灵敏度分析找出该问题的关键参数有助于提高进化算法的搜索效率。

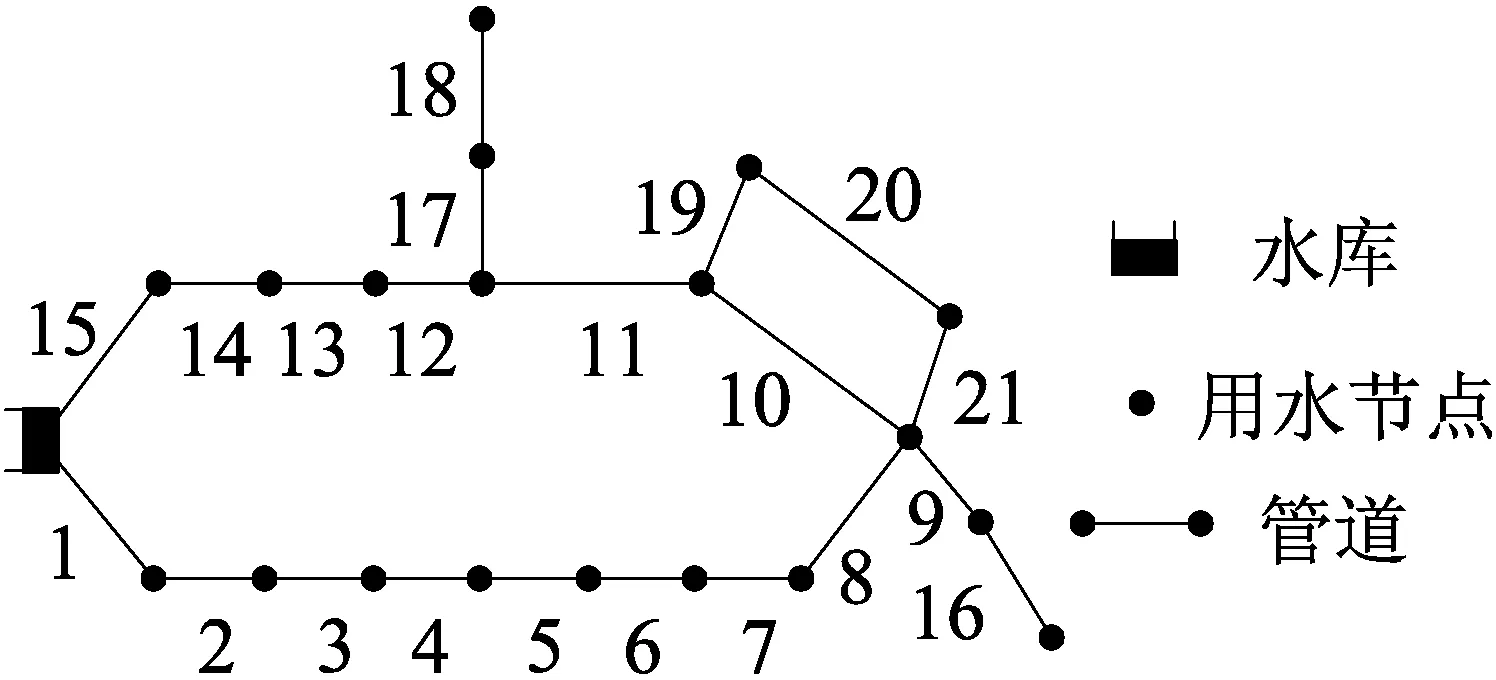
图1 纽约隧道管网

2.2 目标函数和输入参数

采用TODINI E[12]提出的一个指标Fresilience来评估管网扩建方案的可靠性，并将该指标作为输出变量，其计算方法如下：

(6)

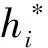
2.3 结果与讨论

2.3.1 Sobol’法分析结果

经过多次取样计算测试稳定性后，取样本次数为N=2 000，共需运行模型N(k+2)=46 000次。分析结果如图2所示，各参数一阶灵敏度和总灵敏度具体数值见表1。为便于区分，对新增管道进行编号，方法如下：1号新增管道即与1号管道平行敷设的新增管道，依此类推。

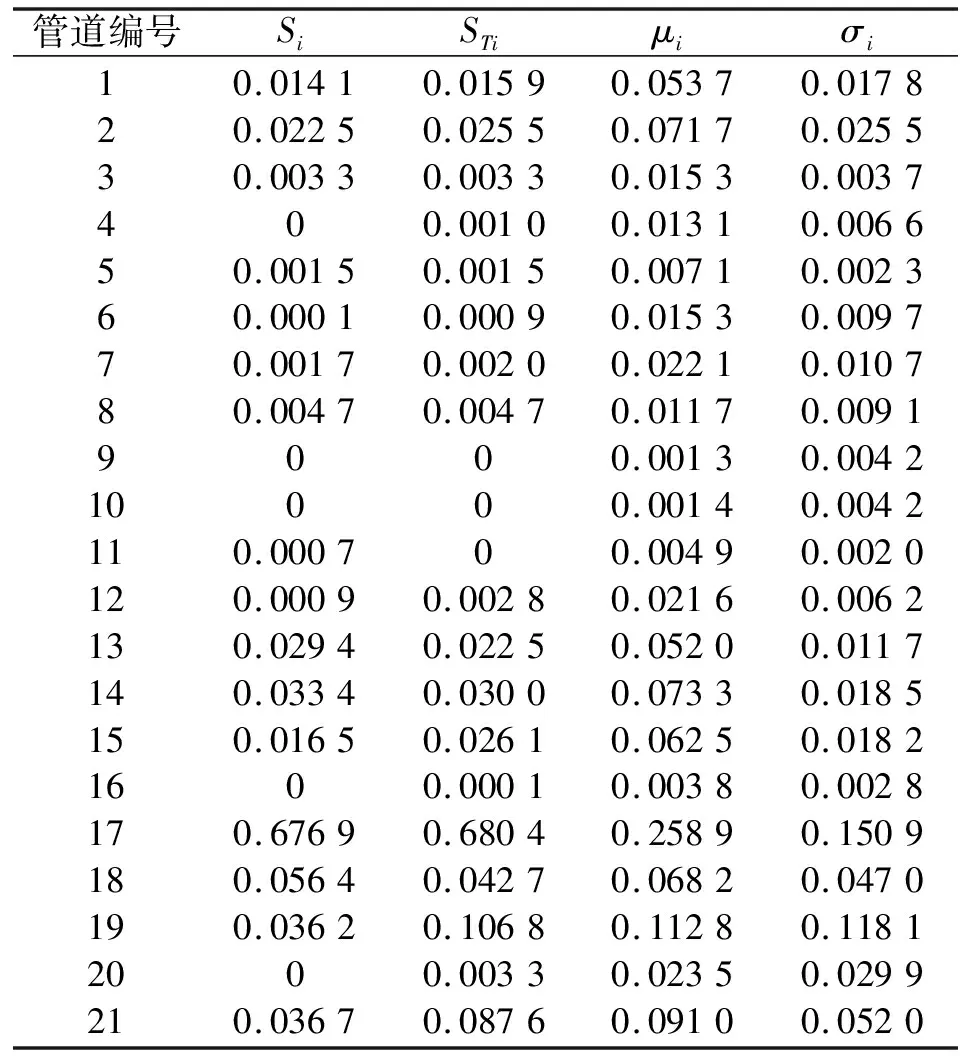
表1 各管道灵敏度值

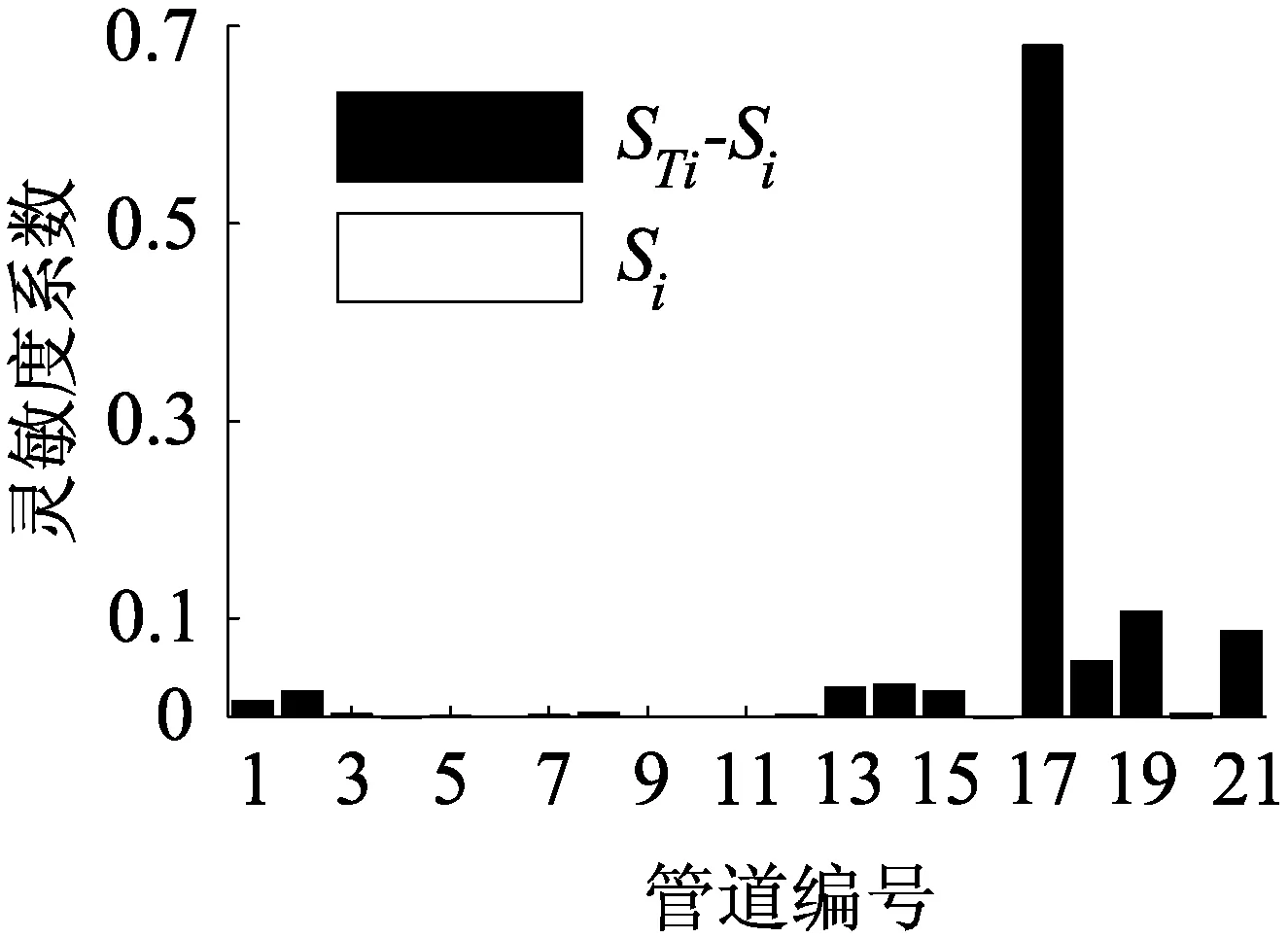
图2 Sobol’法的分析结果

由图2可知，目标管网的可靠性受17号新管管径变化的影响最大，其次为1、2、13、14、15、18、19和21号新增管道，而其余新增管道对管网可靠性的影响非常小，可以忽略；总体上来说，参数间的交互作用对该管网可靠性影响不大。

为验证Sobol’法分析结果的准确性，设置如下4种情况。Case1：考虑所有新增管道的不确定性，即输入变量包括所有新增管道；Case2：只考虑1、2、13～15、17～19和21号新增管道的不确定性，其余新增管道管径取值为8 in(可选管径的中间值)；Case3：只考虑17号新增管道的不确定性，其余新增管道管径取值为8 in；Case4：考虑3～12、16和20号新增管道的不确定性，其余新增管道管径取值为8 in。通过蒙特卡洛模拟对以上4种情况进行不确定性分析，对每种情况均随机取样2 000次，计算后得到纽约隧道管网可靠性的经验累积分布函数(CDF)曲线如图3所示。

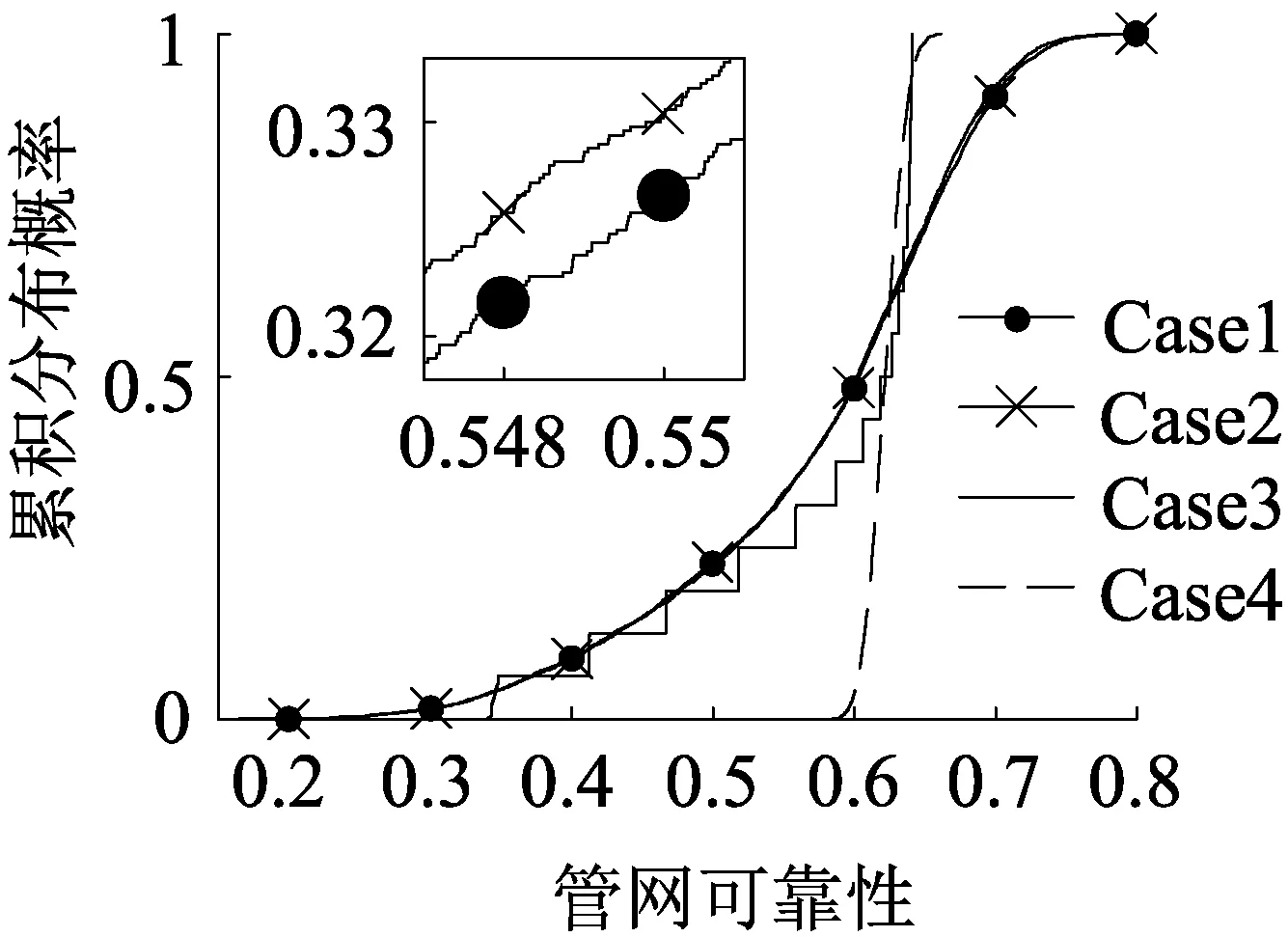
图3 4种情况的累积分布曲线

由图3可知，当仅考虑最重要参数的不确定性(Case3)时，其CDF曲线与考虑所有参数不确定性(Case1)的CDF曲线相比，趋势大致相同；当只考虑重要参数的不确定性(Case2)时，CDF曲线与考虑所有参数不确定性(Case1)的CDF曲线基本一致；而仅考虑不重要参数(Case4)时，其CDF曲线接近于直线，管网可靠性的变化非常小。因此，由Sobol’法分析得到的参数灵敏度是可靠的。

根据总灵敏度对重要管道进行排序，Sobol’法分析得到的管道排序依次为17、19、21、18、14、15、2、13和1。

2.3.2 Morris法分析结果

Morris法参数设置：p=4，r=10。共运行模型r(k+1)=220次，Morris法分析结果如图4所示，各管道灵敏度具体数值如表1所示。由图表可知，3～12、16和20号新增管道的μi和σi值都很小，表明其对管网可靠性的影响很小, 是不重要参数；其余新增管道的μi值和σi值相对较大，表明它们对管网可靠性的影响较大，且其效应的非线性程度较高或与其他参数间存在交互作用，是重要参数。根据μi值对重要管道进行排序，Morris法分析得到的管道排序依次为17、19、21、18、14、15、2、1和13。

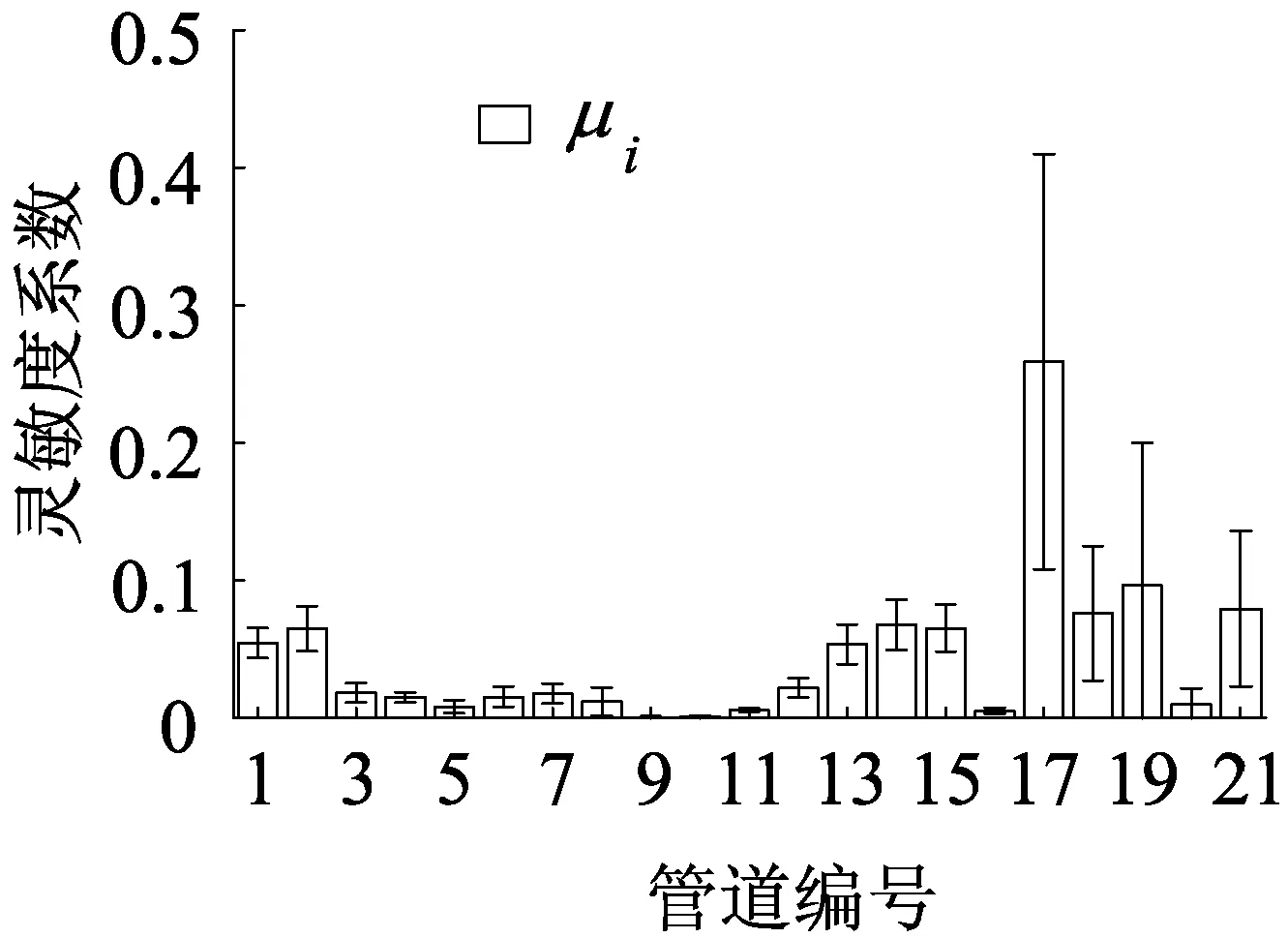
图4 Morris法的分析结果

2.3.3 Morris法与Sobol’法的对比分析

对3～12、16和20号新增管道，Morris法和Sobol’法的分析结果一致，是不重要参数；对于其余重要参数，Morris法分析得到的参数灵敏度排序与Sobol’法所得排序大致相同，但Morris法不能对参数间的交互作用进行详细分析。值得注意的是，虽然Morris法的精度稍差于定量分析的Sobol’法，但其所需样本量远小于后者。也就是说，相对于Sobol’法，Morris法能以较小的计算代价识别重要参数，并获得比较准确的参数灵敏度排序。

3 结论与建议

根据已有研究表明：在基于供水管网模型的分析和设计中，输出结果的不确定性主要受少数重要参数的影响。为提高识别模型中重要参数的效率，本文提出采用Morris法进行全局灵敏度分析。通过纽约隧道案例，从计算效率、计算精度方面对Morris法和Sobol’法进行详细对比，结果表明：Sobol’法虽然能定量评估输入参数对模型输出的影响，但所需计算量大；Morris法精度稍差，但能以较小的计算代价获得参数灵敏度的定性描述，其计算量远小于Sobol’法。

根据管网模型复杂程度和使用目的，对全局灵敏度分析方法的选择提出以下建议：

(1)当管网模型参数较少时(不多于20个)，若需要对各参数的作用进行详细分析，可选择Sobol’法；若只需大致的参数灵敏度排序，可选择Morris法进行分析。

(2)当管网模型输入参数众多时，可考虑先采用Morris法筛选出模型的重要参数，再采用Sobol’法定量分析重要参数对模型输出的影响，以降低计算时耗。