老龄多人口死亡率联合建模与一致性预测
王晓军 赵晓月 陈惠民


摘 要:退休年龄以上的老年人群死亡率预测是养老金精算和长寿风险度量的基础。针对我国大陆地区退休年龄以上人群死亡率数据量较小且波动较大的问题,借助多人口联合建模思想,基于单人口CBD模型,提出了一个适用于老龄死亡率建模的Logistic多人口模型。通过加入更多相关人口数据信息来预测我国老年人口死亡率,选取我国台湾地区分性别死亡率相关数据,与我国大陆地区分性别死亡率数据进行联合建模。研究发现,Logistic多人口死亡率模型比单人口CBD模型表现出更好的拟合效果和长期预测一致性效果。
关键词:老年人口;死亡率;Logistic模型;多人口模型
中图分类号:C921 文献标识码:A 文章编号:1000-4149(2021)02-0045-12
DOI:10.3969/j.issn.1000-4149.2021.00.011
收稿日期:2020-08-28; 修订日期:2021-01-25
基金项目:教育部哲学社会科学研究重大课题攻关项目“健康中国2030背景下的健康老龄化体系优化研究”(20JZD023)。
作者简介:王晓军,中国人民大学应用统计科学研究中心研究员,统计学院教授;赵晓月,中国人民大学统计学院博士研究生;陈惠民,中国人民大学统计学院博士研究生。
Modeling and Coherent Forecasting of the Elderly Mortality
with Multiple Populations
WANG Xiaojun1,2, ZHAO Xiaoyue2, CHEN Huimin2
(1.Center for Applied Statistics, Renmin University of China, Beijing 100872,
China;2.School of Statistics, Renmin University of China, Beijing 100872, China)
Abstract:
The mortality prediction of the elderly above retirement age is the basis of pension actuarial valuation and longevity risk measurement. In order to solve the problem of small amount and large fluctuation of mortality data of people above retirement age in mainland China,
this paper proposes a Logistic
multi-population model for the elderly mortality model based on a single population
Cairns-Blake-Dowd (CBD) model.
By adding more relevant population data information to predict the mortality rate of the elderly population in China, this paper selects the gender specific mortality data in Taiwan and carries out joint modeling with the gender specific mortality rate in mainland China. It is found that compared with single population CBD model, the Logistic multi-population mortality model has a better fitting
and long-term coherent prediction effect.
Keywords:aging population;mortality;Logistic model;multiple population model
一、引言
退休年齡以上的老年人群死亡率预测是养老金精算和长寿风险度量的基础。依据国家统计局公布的数据,截至2019年末,我国60岁及以上老年人口数达到2.54 亿人,占总人口的比例超过18%。人口预期寿命逐年增加,2015年我国男、女性出生预期寿命分别达到73.64岁和79.43岁。另外,依据联合国《世界人口展望2019年》的预测结果,未来人口预期寿命仍然保持约每5年增加一岁的趋势,人口预期寿命增长的不确定性给养老金风险管理带来挑战。
在我国,分年龄的死亡人数和生存人数来源于人口普查和人口抽样调查,除了每10年的人口普查和每5年的1%人口抽样调查,其他年份均是千分之一左右的人口变动抽样调查,对应的分年龄性别人数较少,分年龄性别的死亡率波动较大。用这些数据直接建模,很难捕捉死亡率随年龄和时间的变动规律。
考虑到人类死亡率变动具有共同规律性的特点,近年来,研究者开始关注对多人口死亡率的联合建模。这里的多人口指研究人群范围为两个或两个以上的具有相似特征的不同人口群体,可以是具有相似经济文化背景或地理位置相近的国家或地区,也可以是同一地区的不同种族或性别。有学者指出,密切相关人群的死亡率模式和轨迹可能类似,可以通过考虑多人口的联合建模方式来提高个别国家的死亡率预测精度[1]。
多人口死亡率模型一般包括公共因素项和附加的特定因素项,公共因素描述整个人口死亡率随时间变化的主要长期趋势,附加因素考虑不同人口的短期差异。多人口死亡率模型可以分为三大类:一是对男女性联合建模,能够有效避免男女死亡率在中长期预测中出现死亡率交叉或分离的不合理问题;二是对不同国家或地区的多个人口进行死亡率联合建模,以达到长期的一致性预测;三是对不同国家和地区的不同性别人口死亡率进行联合建模,既考虑不同人口间的协整关系,又保证同一人口不同性别间的相依关系。
我国大陆地区高龄人口死亡数据的时间序列短,分年龄性别的风险暴露人数少,死亡率数据的波动性较大,因此在现有大陆地区人口死亡率数据的基础上,加入更多相关人口数据信息,可以实现对我国高龄人口死亡率更好地建模和预测。本文基于CBD模型和Logistic两人口死亡率模型,提出一种包括分地区和分性别的老龄多人口死亡率模型,在性别因子的基础上加入国别和地区别因子,假设死亡人数服从泊松分布,利用极大似然估计进行参数估计。
选择人种相同、地理位置相近的中国大陆、中国台湾分男女共四类人口的数据进行联合建模,通过捕捉死亡率变动的共同规律,拟对中国大陆人口死亡率做出更合理预测。
二、死亡率模型的研究综述
早期的死亡率模型只是能描述死亡率随年龄变动的静态模型,之后死亡率模型中加入时间项,发展为单个人口动态模型,动态死亡率模型的典型代表是1992年提出的 Lee-Carter 模型[2],该模型假设对数死亡率由年龄效应、时间效应以及与年龄相关且与时间有交互效应的项组成,因其形式简单且参数的可解释性强等特点被广泛应用。之后,有许多研究在Lee-Carter 模型基础上进行了扩展。伦肖(Renshaw)等在Lee-Carter模型的基础上加入了队列效应,对于过去观察到队列效应的国家,该模型可以更好地拟合历史数据[3]。柯里(Currie)提出了含有年龄、时期、队列的Age-Period-Cohort(APC)模型,该模型可以视作伦肖所提
模型的简化形式,模型不需要平滑性的条件,消除了可能存在的稳健性问题[4]。凯恩斯(Cairns)等又提出了适用于高龄死亡率的CBD(Cairns-Black-Dowd)模型,CBD模型引入了两个时间效应因子,区分了高年龄人群的死亡率随时间的改善效应,使模型对高年龄段的拟合和预测效果更好[5]。凯恩斯等人在CBD模型的基础上,考虑二次项和队列效应项,给出了一些CBD扩展模型,并指出加入二次项和队列项的模型拟合效果更好[6]。
随着研究的进行,研究者发现单人口死亡率模型在死亡率的长期预测中容易出现不合理的交叉或偏离情况,有违人类死亡率变动的一般规律性,从而提出多人口联合建模和预测的思路。有学者在Lee-Carter模型基础上进行扩展,提出了公共因子(Common Factor,CF)模型及增广公因子(Augmented Common Factor,ACF)模型,它包含了整个人群的一个共同因素,以及扩展模型中的一个额外的性别特定因素[1]。公共因素描述了整个人口死亡率随时间变化的长期主要趋势,附加因素考虑了每个性别的短期差异。使用公共因子模型避免了不同人口死亡率随时间出现的交叉或偏离问题,并确保根据观察到的历史模式,每个年龄段的男性死亡率与女性死亡率的比率在长期收敛到一个常数。又有学者使用泊松分布直接对死亡人数建模,同时将模型结构广义化,提出了泊松公共因子模型(Poisson Common Factor Model,简称PCFM模型),该模型为数据分析、参数估计和模型选择提供了严格的统计框架,同时模型可以扩展为多个特定因素,可以更好地捕获残差中的其他系统特征[7]。他们利用10个人口死亡率数据,进一步评估了泊松公共因子模型的拟合和预测性能,结果表明,该方法能确保每个年龄段的男女死亡率在长期内收敛到一个常数,并提供更准确的男女死亡率预测[8]。此后,又有学者在扩展公共因子模型的基础上加入了国别(不同国家或地区)因子,提出了两层扩展公共因子模型,并使用英国的英格兰和威尔士、苏格兰和北爱尔兰的数据,对模型进行了验证,对死亡率作出了一致的预测[9]。
学者们又对单人口CBD 模型进行扩展,在截距项和斜率项中分别加入了性别参数,提出了一个适用于高龄的Logistic两人口死亡率模型,并使用模型对比利时、瑞典、瑞士、英国四个国家的高龄死亡率数据进行建模预测,取得了良好的拟合和预测效果[10]。
三、Logistic死亡率模型
1. CBD模型
凱恩斯等人提出的CBD模型是一种单人口Logistic动态模型,适用于高龄人群死亡率的拟合和预测[5]。模型形式如下:
logit(qx,t)=κ(1)t+(x-)κ(2)t+εx,t(1)
其中,qx,t是t年x岁的死亡概率,κ(1)t、κ(2)t是两个时间项,εx,t为随机误差项。
2. Logistic两人口死亡率模型
如前所述,采用单人口模型对男性和女性高龄人口死亡率进行单独建模和预测时往往在预测期内会出现两性别死亡率的交叉或分离等脱离实际的现象,因此需要考虑对两性别死亡率的联合建模。
2019年,学者们提出适用于高龄的Logistic两人口死亡率模型[10],模型形式如下:
logitq(i)x,t=αt+βt(x-)+τ(i)t+ν(i)t(x-)(2)
其中,q(i)x,t表示x岁的人在时间t的死亡概率,i代表性别(i=1代表女性,i=2代表男性),αt和βt是两个性别的共同参数,τ(i)t和υ(i)t是分性别参数,αt+τ(i)t和βt+υ(i)t分别代表死亡率曲线对性别i在时间t的截距项和斜率项。表示建模年龄段的平均年龄。
在模型(2)的基础上加入个体曲率项可以进一步扩展为模型(3),具体形式如下:
logitq(i)x,t=αt+βt(x-)+τ(i)t+ν(i)t(x-)+γ(i)t[(x-)2-σ2](3)
其中,γ(i)t是关于性别i的曲率项,σ2是建模所覆盖的年龄范围下(x-)2的均值。如果男女之间的曲率相似,即第三项为公共曲率项,则模型(3)可简化为模型(4):
logitq(i)x,t=αt+βt(x-)+τ(i)t+ν(i)t(x-)+γt[(x-)2-σ2](4)
其中,γt为两性别的共同参数项。
3. Logistic多人口死亡率模型
以上两人口模型可以避免男女死亡率随时间的交叉问题,但没有考虑不同人口之间死亡率的长期一致性。本文在Logistic两人口死亡率模型的基础上,加入人口别(不同国家或地区)因子,提出一种Logistic多人口死亡率模型,既考虑不同人口之间的协整关系,又考虑性别间的相依关系,构建高维多人口死亡率模型,捕捉人类死亡率变动的共同规律,使对不同人口的死亡率预测具有一致性。模型形式如下:
logitqx,t,i,j=αt+βt(x-)+τt,i,j+νt,i,j(x-)(5)
其中,qx,t,i,j表示x岁的人在时间t的死亡概率,i代表性别(i=1代表女性,i=2代表男性),j=n表示n个不同的人口(国家或地区)数据, αt和βt是共同参数,τt,i,j和υt,i,j是分性别参数。
αt+τt,i,j和βt+υt,i,j分别代表死亡率曲线对性别i在时间t的截距项和斜率项,表示建模年龄段的平均年龄。
在模型(5)的基础上加入分性别分人口曲率项可以进一步扩展为:
logitqx,t,i,j=αt+βt(x-)+τt,i,j+νt,i,j(x-)+γt,i,j
[(x-)2-σ2](6)
其中,γt,i,j是关于性别i人口j的曲率项,σ2是建模所覆盖的年龄范围下(x-)2的均值。
为确保死亡率预测的一致性,假设共同的参数遵循带漂移的随机游走,性别参数和人口别参数均遵循自回归过程AR(1):
αt=δ1+αt-1+εt,1(7)
βt=δ2+βt-1+εt,2(8)
γt=δ3+γt-1+εt,3(9)
τt,i,j=φ(i,j)0,1+φ(i,j)1,1τt-1,i,j+ω(i,j)t,1(10)
υt,i,j=φ(i,j)0,2+φ(i,j)1,2υt-1,i,j+ω(i,j)t,2(11)
γt,i,j=φ(i,j)0,3+φ(i,j)1,3γt-1,i,j+ω(i,j)t,3(12)
其中,δ1,δ2和δ3是漂移项,φ(i,j)0,1,φ(i,j)0,2和φ(i,j)0,3是截距项,φ(i,j)1,1,φ(i,j)1,2和φ(i,j)1,3是自回归参数,εt,1,εt,2,εt,3,ω(i,j)t,1,ω(i,j)t,2和ω(i,j)t,3是正态误差项。它们相互关联,跨时间独立。
4. 参数估计方法
运用极大似然估计方法
估计参数,以模型(6)为例,假设死亡人数服从泊松分布:
Dx,t,i,j~Poisson(ex,t,i,j μx,t,i,j)(13)
其中,Dx,t,i,j是死亡人数,ex,t,i,j是中心暴露数。令logitμx,t,i,j=ηx,t,i,j,则μx,t,i,j=exp(ηx,t,i,j)/[1+exp(ηx,t,i,j)]。似然函数为:
l=∑x,t,i,j[dx,t,i,jlnex,t,i,j+dx,t,i,jlnμx,t,i,j-ex,t,i,jμx,t,i,j-ln(dx,t,i,j!)](14)
参数估计迭代更新方程为:θ*=θ-lθ/l2θ2,迭代更新步骤如下。
步骤1:设置参数初始值(建议αt=-2,βt=0.1,τx,t,i,j=0,νx,t,i,j=0,γx,t,i,j=0),并计算所有的μx,t,i,j和ηx,t,i,j的拟合值;
步骤2:对所有的t更新αt,然后重新计算所有μx,t,i,j和ηx,t,i,j的拟合值;
步骤3:对所有的t更新βt,然后重新计算所有μx,t,i,j和ηx,t,i,j的拟合值;
步骤4:对所有i和t更新τx,t,i,j,然后重新计算所有μx,t,i,j和ηx,t,i,j的拟合值;
步骤5:对所有i和t更新νx,t,i,j,然后重新計算所有μx,t,i,j和ηx,t,i,j的拟合值;
步骤6:对所有i和t更新γx,t,i,j,然后重新计算所有μx,t,i,j和ηx,t,i,j的拟合值;
步骤7:对所有i和t,调整α*t=αt+cτ和τ*t,i,j=τt,i,j-cτ,其中cτ=∑tτ(1)t/Nt,Nt为年数;
步骤8:对所有i和t,调整β*t=βt+cτ和υ*t,i,j=υt,i,j-cυ,其中cν=∑tν(1)t/Nt,Nt为年数;
步骤9:计算对数似然函数;
步骤10:重复步骤2到9,直到对数似然函数收敛。对于其他形式的模型,可以简单修改上面的一些步骤,实现参数估计。
四、死亡率联合建模
1. 数据描述
中国大陆人口死亡率数据来自历年《中国人口统计年鉴》和《中国人口和就业统计年鉴》,目前公布的数据有1994—2018年共25年连续数据。其中2000年和2010年为全国人口普查数据,1995年、2005年、2015年为全国1%人口抽样调查数据,对于普查年数据和1%人口抽样调查数据,分年龄分性别有0岁到100岁及以上数据。其他年份为1‰左右变动抽样数据,其中1996年数据从0岁到85岁及以上,对于85—89岁死亡率采用插值法处理,其他年份数据从0岁到90岁及以上。
中国台湾人口死亡率数据来自人类死亡率数据库HMD(Human Mortality Database),根据公布的分年龄分性别数据,台湾地区有1970—2014年共45年连续数据,台湾地区分年龄分性别数据从0岁到110岁及以上。相比中国大陆地区而言,中国台湾地区的死亡率数据时间段较长,数据质量较高。柳向东等认为我国大陆地区和台湾地区人口死亡率存在长期均衡关系[11]。段白鸽指出我国大陆和台湾地区各年龄死亡率、平均预期寿命之间的差异明显缩小,未来死亡率呈现趋同化发展[12]。因此我们选择中国大陆和中国台湾分性别老龄数据进行联合建模,对中国大陆老龄人口死亡率数据进行修匀和预测。
2. 模型拟合和模型选择
我们选择中国大陆、中国台湾共同数据区间1994—2014年男性和女性分年龄60—89岁死亡率数据进行联合建模。考虑到中国大陆人口基数较大,为了充分利用死亡率信息,以中国大陆地区的风险暴露数为基准,按1∶1的比例调整中国台湾地区的风险暴露数,再以台湾地区的中心死亡率调整死亡人数,最后运用极大似然方法对死亡人数进行建模。
选择赤池信息准则(Akaike Information Criterion,AIC)和贝叶斯信息准则 (Bayes Information Criterion,BIC)来评估模型的拟合效果。其中,
AIC=2k-2ln(L)(15)
BIC=kln(n)-2ln(L)(16)
其中,k为模型参数个数,n为样本量,L为似然函数。AIC准则和BIC准则的区别在于BIC准则考虑了样本量,对模型复杂度的惩罚力度更大,当样本量较大时,可以有效防止模型拟合精度过高而造成的模型复杂度过高的现象。AIC和BIC值越小模型效果越好。
表1给出了Logistic多人口模型的2个模型拟合得到的AIC值和BIC值。模型(6)的AIC和BIC值均比模型(5)小了大约13%,因此选择模型(6)对数据进行建模。
我们还可以通过计算样本内平均绝对百分比误差(Mean Absolute Percentage Error, MAPE)来评价模型的拟合效果,MAPE表达式为:
表2给出了模型(1)—模型(6)中国大陆、中国台湾拟合结果的MAPE值,其中模型(1)为单人口CBD模型,模型(2)、(3)为仅加入性别项的两人口模型,模型(5)、(6)为加入了性别项和人口项的多人口模型。结果显示,无论是男性还是女性,加入性别项的两人口模型与同时加入性别和人口项的多人口模型的MAPE值相同,均小于单人口CBD模型,而加入曲率项的模型(3)和模型(6)的男女死亡率拟合结果均优于没有加曲率项的模型。与CBD模型相比,在模型(6)下的拟合结果中国大陆男女MAPE值分别减小了6%和5.5%,中国台湾男女MAPE值分别减小了46%和35.7%,拟合效果有明显改善。
运用模型(6)对数据进行联合建模,图1给出了模型(6)的拟合残差图,可见,中国大陆、中国台湾男女的残差分布均满足随机性。对于中国大陆而言,可以看到数据质量较好的普查年份和1%抽样调查年份的残差明显较小,说明模型对这部分的数据拟合效果较好,这也符合我们的预期结果。对于中国台湾而言,整体拟合残差值较小。
图2给出了模型(6)下中国大陆男女死亡率原始数据和修匀结果,可以看出模型(6)修匀效果有较好的光滑性,男女死亡率随时间变化呈递减趋势。
对于上述拟合结果,考虑到我国大陆地区分年龄死亡率波动性较大,高龄部分数据稀疏的情况,我们选择数据量较大,数据质量较好的普查年和1%抽样调查年的1995年、2000年、2005年、2010年四年的分性別死亡率数据,将几个模型的拟合结果做对比。表3给出了中国大陆地区这四个年份分性别拟合结果的MAPE值。结果表明,对于中国大陆地区,模型(6)对数据拟合优于CBD模型,而且对于数据质量较好的年份,男女MAPE值分别减少了29%和25.85%,拟合结果也优于单人口的CBD模型。
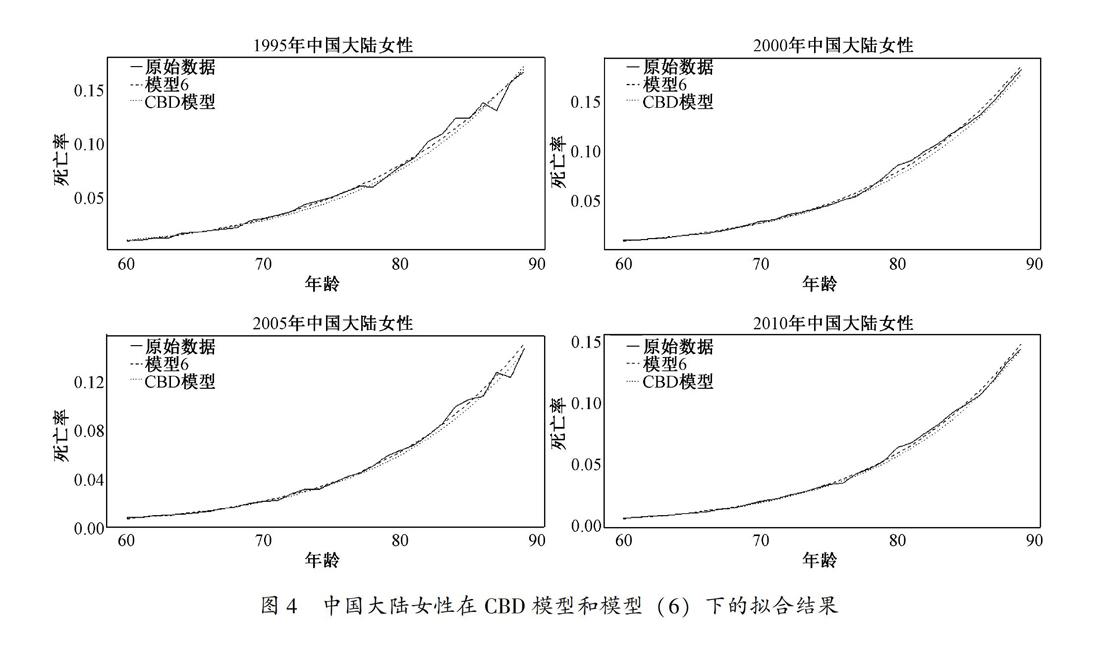
图3、图4分别给出了中国大陆地区男性和女性在CBD模型和模型(6)下1995年、2000年、2005年、2010年的拟合效果图。可见,无论是男性还是女性,CBD模型拟合结果均低于模型(6),模型(6)在CBD模型的基础上提高了拟合精度。
3. 死亡率预测
在死亡率预测中,为确保预测一致性,假设共同的参数遵循带漂移的随机游走,性别参数和人口别参数均遵循自回归过程AR(1)。图5给出了共同参数αt和βt的估计和预测结果,参数αt反映了死亡率整体下降的趋势,参数βt呈缓慢下降趋势。图6给出了中国大陆分性别参数的估计和预测结果,可以看到分性别和人口别的参数在弱平稳过程下收敛到常数,同时也给出了参数的95%预测区间。
使用上述参数预测值,可以对死亡率做出预测,将死亡率外推到2050年,并与单人口死亡率预测结果进行对比。图7给出了中国大陆地区、中国台湾地区在CBD模型、模型(3)、模型(6)下2050年的分性别分地区的预测结果对比图。图中CBD模型死亡率曲线从上到下依次为中国大陆男性、中国台湾男性、中国大陆女性、中国台湾女性,可以看到在长期预测中,CBD模型男女死亡率产生偏离现象;模型(3)结果显示男女死亡率呈现一致性预测,男女死亡率曲线趋于平行,但不同人口之间死亡率差异性较明显;模型(6)的结果显示,男女死亡率呈现一致性预测,男女死亡率曲线趋于平行,且不同人口之间死亡率也呈现一致性预测。
在模型(6)参数估计的结果下,可以计算得出中国大陆地区男女死亡率预测值。表4给出了2020年、2030年、2040年、2050年的60—89岁死亡率预测值。可见,随着时间推移,男女死亡率均呈下降趋势,60岁男性死亡率从2020年的0.0105降到了2050年的0.0075,大约降低28.6%;60岁女性死亡率从2020年的0.0058降到2050年的0.0043,约降低25.9%。同一时期女性死亡率明显低于男性,随着时间推移男女死亡率差距逐渐减小。
五、结论
本文在CBD模型和Logistic两人口死亡率模型基础上对模型进行扩展,在分性别因子
基础上加入国家和地区别因子,提出了Logistic多人口模型,用于对多个人口分性别的联合建模,以捕捉不同人口死亡率的共同特性,更好地预测死亡率变动趋势。模型打破了单人口模型与两性别或多人口联合建模的局限,将性别与人口别同时联合建模,将模型推向高维。
针对中国大陆地区高龄死亡率数据波动大,数据质量差的问题,我们选择中国大陆地区、台湾地区
分男女死亡率相关数据,以中国大陆数据为基础,并按1∶1数据量调整台湾数据,对其进行联合建模和预测,来拟合和预测中国大陆未来死亡率变化模式;与单人口CBD模型相比,从拟合结果MAPE值来看,中国大陆、中国台湾男女死亡率拟合效果均有所改善。在长期预测中,Logistic多人口模型避免了单人口CBD模型可能出现的死亡率交叉或偏离问题,能够给出死亡率的一致预测。
在进一步的研究中,Logistic多人口模型还可以尝试加入队列效应对模型进行扩展,以适用于能够捕捉到队列效应国家或地区的数据;
也可以采用贝叶斯技术,该技术可以提供合理的框架来同时处理死亡率结构和时间序列过程。
参考文献:
[1]LI N,LEE R.Coherent mortality forecasts for a group of populations: an extension of the Lee-carter method[J]. Demography, 2005,42(3):575-594.
[2]LEE R D, CARTER L R. Modeling and forecasting U.S. mortality[J]. Journal of the American Statistical Association, 1992,87(419): 659-671.
[3]RENSHAW A E, HABERMAN S. A cohort-based extension to the Lee-carter model for mortality reduction factors[J]. Insurance: Mathematics and Economics, 2006, 38(3):556-570.
[4]CURRIE I D. Smoothing and forecasting mortality rates with p-splines[R]. Institute of Actuaries, 2006.
[5]CAIRNS A J G, BLAKE D, DOWD K. A two-factor model for stochastic mortality with parameter uncertainty: theory and calibration[J]. Journal of Risk and Insurance,2006,73(4): 687-718.
[6]CAIRNS A J G, BLAKE D, DOWD K et.al. A quantitative comparison of stochastic mortality models using data from England & Wales and the United States[J]. North American Actuarial Journal,2009,13(1):1-35.
[7]LI J.A poisson common factor model for projecting mortality and life expectancy jointly for females and males[J]. Population Studies,2013,67(1):111-126.
[8]LI J, TICKLE L, PARR N.A multi-population evaluation of the poisson common factor model for projecting mortality jointly for both sexes[J]. Journal of Population Research,2016, 33(4):333-360.
[9]CHEN R Y, MILLOSSOVICH P. Sex-specific mortality forecasting for UK countries:a coherent approach[J]. Eur.Actuar.J,2018,8(1):69-95.
[10]LI J, LIU J. A Logistic two-population mortality projection model for modelling mortality at advanced ages for both sexes[J]. Scandinavian Actuarial Journal, 2019(2):97-112.
[11]柳向東,范洋洋. 基于均衡关系的中国人口死亡率预测模型[J].统计与信息论坛,2016(10):3-9.
[12]段白鸽.我国全年龄段人口平均预期寿命的动态演变[J].人口与经济,2015(1):49-63.
[责任编辑 刘爱华]

