基于函数型特征数据的光伏短期功率预测方法

张林，刘继春，马靖宇，周晟锐，文杰

（四川大学电气工程学院，四川 成都 610065）

近年来，伴随信息化建设的飞速发展和储存收集设备的不断完善，电力行业数据呈现出来的形式不再是离散、稀疏的片段点集，而是表现为连续、紧密的函数曲线特征[1]，“函数”并非代表外在直观特征的展现，而是指观测收集的离散数据具有函数本征连续结构，将此类具有函数型特征的数据称为函数型数据[2]。并且，随着能源互联网的大力推进，许多地区开始推行多种能源综合发电，如梯级水光蓄互补综合发电系统[3]，利用梯级水电和抽水蓄能出力的可控特性，去调控优化光伏出力的随机波动性，以此提高能源的综合利用率，减少弃光、弃水量。抽水蓄能调控能力技术可达min级，而光伏出力受天气因素影响，具有较强的随机性和不可控性，因此，准确的min级别光伏短期预测是调控水电和抽水蓄能运行方式的重要依据。

目前，光伏特性分析预测已有不少研究。文献[4]从影响光伏出力因素的角度出发，使用模糊C均值（fuzzy C-means，FCM）对历史太阳辐射和温度进行聚类分析，通过典型式子将太阳辐射和温度转化为光伏出力，并进行特性分析。文献[5]将光伏数据预处理成多个样本子集，使用K-means将数据划分为三类，依靠聚类中心挖掘光伏波动性和规律性。文献[6]基于传统的K-means结合层次聚类方法，研究了光伏数据的相似性。文献[7]分别分析了辐射、温度、风速、空气质量单一因素和其两两组合因素对光伏出力的影响，并基于回归方法建立了光伏出力预测模型。文献[8]利用K-means将样本训练成多个子集，对不同类别的子集分别使用支持向量机（support vector machine，SVM）进行预测，但通过经验设置SVM的参数存在一定的偶然性和误差。文献[9]提出使用改进的粒子群优化-支持向量机（partical swarm optimization-support vector machine，PSOSVM）方法对光伏进行预测，虽通过PSO寻优降低了因经验选取参数而导致的SVM模型误差，但光伏出力随天气变化差异较大，使用单一模型不具有普适性。文献[10]结合历史气象和光伏数据，将光伏数据分为晴、多云、阴和雨四种典型场景，利用分散搜索-支持向量机回归（scatter search-support vactor regerssion，SS-SVR）算法对四种天气分别建模预测。

考虑不同天气类别光伏输出功率差异较大，上述多数文献在光伏预测方面，对光伏数据都进行了预处理，目的是为了减少预测的计算时间和提升预测精度，样本精度通常为15 min或1 h。而现阶段对于具有函数型特征的1 min级光伏出力预测研究还较少。传统预测方法[11]，如灰色轨迹、BP神经网络和SVM等预测模型仅适用于小样本数据的训练。

针对上述问题，提出利用傅里叶基函数将具有函数特征的光伏离散数据转换为函数数据，提取光伏形态趋势序列；利用函数主成分分析（functional principal component analysis，FPCA）将集成的函数曲线进行函数主成分降维分析，用低维的函数主成分特征向量对原始高维数据进行直观表达；并结合高斯混合模型最大期望（gaussian mixture model-expectation maximum，GMMEM）算法对函数主成分特征矩阵进行聚类，提取聚类簇形态中心和均值中心突出典型场景类型，结合天气数据验证聚类效果。

最后，分别对聚类形成的各光伏场景建立改进粒子群优化-极限学习机（partical swarm optimization-extreme learning machine，PSO-ELM）算法预测模型。

1 基于函数型光伏历史数据的预测总体框架

现阶段已经建成或者正在修建的光伏电站，配备的数据采集装置精度可达到min级别，能将光伏出力过程实时高频的刻画出来。针对此类数据，提出以下聚类处理与预测分析的总体流程框图，如图1所示。

图1 算法总体框架图Fig.1 Algorithm overall framework

由图1中可以看出：

1）光伏数据预处理部分，选取傅里叶基函数作为转换模型，通过傅里叶基函数将离散的光伏数据转换为函数型数据；利用FPCA对函数型数据降维，提取函数主成分对应的特征系数，用少量代表曲线特征的特征向量来替代函数型光伏数据特征。

2）光伏数据聚类分析部分，利用GMM-EM算法将光伏函数主成分特征向量快速准确分类，提取簇类别中心与均值中心突出各种类别的差异性和独特性。

3）光伏数据预测分析部分，从GMM-EM算法得到光伏聚类分组结果1，…，n，选取处理海量数据性能优越的ELM神经网络作为函数型光伏数据预测模型，并利用改进PSO算法寻求ELM网络中的参数，分别对聚类分组结果1，…，n建立改进PSO-ELM算法预测模型。

2 光伏数据预处理模型

2.1 傅里叶基函数

光伏历史数据的完整性是进行数据分析的前提，首先筛选剔除缺失片段数据。傅里叶基函数适用于周期性的观测数据[12]，鉴于光伏数据呈正弦波形，且日光伏出力曲线也具有一定的周期性，故采用傅里叶基函数对其进行转换。

用X=[x1,x2,…,xn]T代表光伏的日出力数据，其第i天光伏数据xi的近似展开形式为

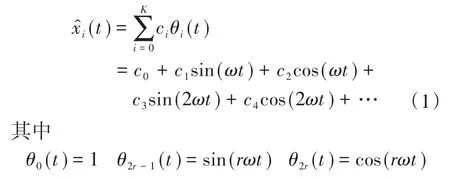
式中：ci为权重系数；K为展开序列的傅里叶级；ω为基角频率；r为基角频率的倍数。

2.2 基于FPCA的光伏数据降维

主成分分析是多元数据的一种重要的降维方法，这种降维思想推广到函数型数据就称为函数主成分分析[13]，基于FPCA的光伏数据降维，具体步骤如下：

3）求解光伏日出力曲线协方差函数的特征值和特征向量，如下式所示，具体求解过程参考文献[14]。

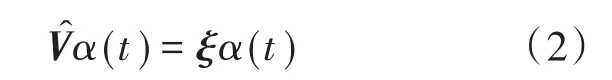
式中：ξ为光伏日出力曲线函数主成分的特征向量；α(t)为光伏日出力曲线函数主成分。

4）将求取的函数主成分对应的特征值按由大到小顺序排列得到 ξ1,ξ2,…,ξn，计算所有特征值的累积贡献率，通常选取D＞85%时前m个特征值，光伏函数主成分特征向量为

3 基于GMM-EM算法的光伏数据聚类模型

3.1 GMM-EM算法

GMM-EM算法能够精确快速将数据分类，本文采用该模型对降维后的光伏数据特征向量进行聚类分组，假定光伏特征向量服从有限个高斯分布的线性组合。

每一个输入高斯分布参数的极大似然表达式如下式所示：

式中：P(α|Θ)为高斯分布的最大似然函数；Θ为GMM的参数集合。

对于GMM的聚类分组实质上就是求取GMM模型中的参数，关于E-step和M-step具体求解步骤参考文献[15]，GMM-EM聚类算法的流程框图如图2所示。

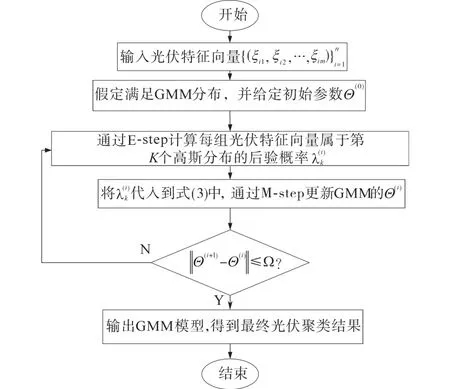
图2 GMM-EM聚类算法的流程图Fig.2 Flow chart of GMM-EM clustering algorithm

GMM中最优聚类个数的确定，通过贝叶斯信息准则（Bayesian information criterion，BIC）进行选取，如下式所示：

式中：logP(α|Θ)为由k个高斯成分混合成的模型对数似然函数；n为样本量；γ为未知参数个数。极大化BICΘ得到的Θ对应最优的模型参数。

3.2 光伏聚类簇的形态模型提取

为了突出光伏数据通过GMM-EM算法聚类分组后类别的差异性和独特性，从各个类别中提取典型光伏曲线表征该类型数据特征，参考文献[16]选取类别均值中心与形态中心。

4 基于改进PSO-ELM的光伏预测模型

ELM作为一种单隐含层前馈神经网络算法，不仅适应性强、训练样本速度快，而且对于大数据样本适应性较好。但该算法输入层权值与隐含层阈值随机产生，稳定性较弱[17]。因此，利用改进PSO算法寻求ELM神经网络中的输入权值和隐藏层阈值，提高模型的预测精度和稳定性。

4.1 改进PSO算法

为防止标准PSO算法陷入局部最优，对标准PSO算法做出以下改进：

1）引入平均粒子距离D(t)，当平均粒子距离小于某一阈值判断粒子是否陷入局部最优。

2）引入动态学习因子c1,c2和惯性权重w。具体改进如下所示：

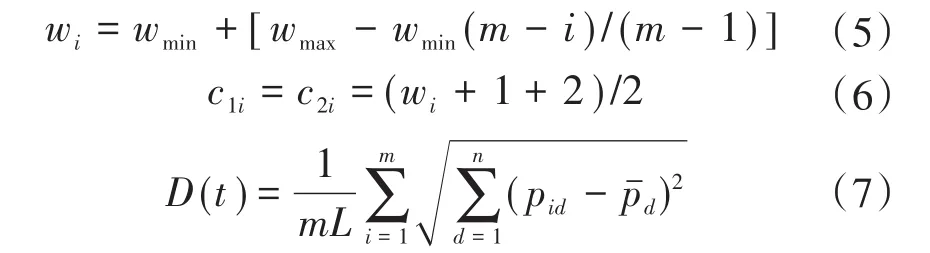
式中：wmax为最大惯性系数；wmin为最小惯性系数；L为搜索空间对角最大长度；m为解空间维数；pid为光伏数据在ELM神经网络训练参数第i个粒子位置的第d维坐标值；为光伏数据在ELM神经网络训练参数粒子在第d维坐标的均值。

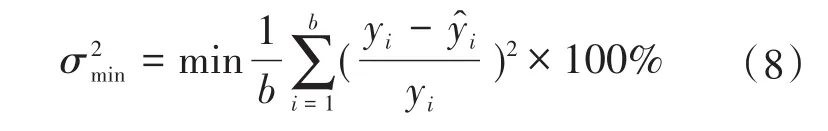
4.2 ELM神经网络

ELM神经网络结构主要分为三层，分别为天气数据输入层、隐含层和光伏出力输出层，如图3所示。

图3中，输入、输出关系如下式所示：

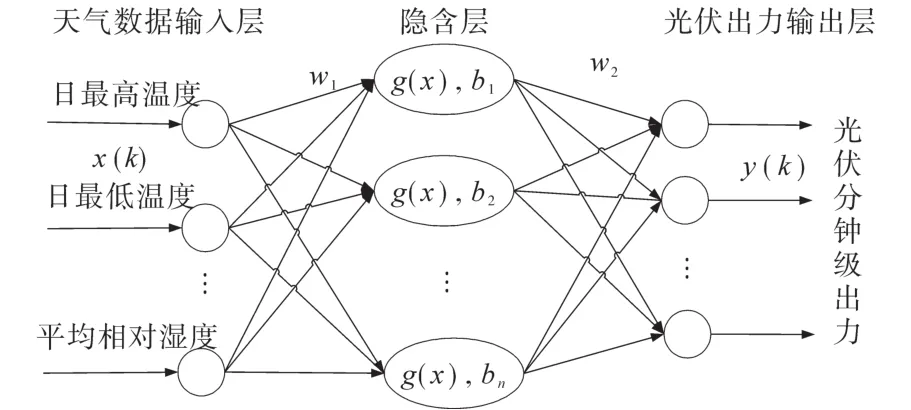
图3 ELM神经网络结构框图Fig.3 ELM neural network structure block diagram

式中：x(k)为天气数据，包括最高气温、最低气温、平均气温、平均相对湿度及日照小时数等；y(k)为每天min级光伏出力数据；w1，w2分别为输入层到隐含层、隐含层到输出层的权值；L为隐含层节点数；bi为第i个隐含层节点的阈值；gi(·)为第i个隐含层节点的激励函数。

当激活函数g(·)能够无误差的逼近输出光伏出力样本，此时：

上述方程的矩阵表达式：

式中：H为ELM神经网络隐含层到输出层的权值矩阵；T为期望的min级光伏出力向量。

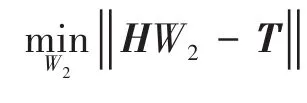
式中：H+为隐含层输出矩阵H的逆矩阵。

4.3 改进PSO-ELM预测模型

本文首先利用改进PSO算法寻求ELM神经网络算法中的输入权值和隐藏层阈值，再采用ELM算法训练样本，提高ELM神经网络的稳定性和精确性，其预测流程如图4所示。

图4 改进PSO-ELM预测模型流程图Fig.4 Flow chart of improved PSO-ELM prediction model

选取天气数据和光伏min级出力数据，将数据归一化处理，划分ELM神经网络的训练样本和测试样本，天气数据作为ELM算法输入层，min级光伏出力作为ELM算法输出层，进而确定ELM神经网络的结构。

通过PSO算法寻求ELM模型的输入层权值和隐含层阈值，把ELM训练输出光伏出力与期望光伏出力误差比值平方作为改进PSO算法适应度函数σ2，计算各个粒子的适应度值，找到对应的粒子速度和位置，并设置平均粒子距离D()t阈值避免PSO算法陷入局部最优。最后，将寻求的最优粒子输入层权值和隐含层阈值赋值ELM神经网络中，得到光伏的预测模型。

5 算例分析

本节数据来源于四川省某地区国家综合能源示范区。选取2017年9月14日～2018年11月17日该地区的天气与历史光伏出力作为原始数据。

光伏出力数据时间尺度为1 min；因影响光伏出力的天气因素较多，本文选取影响功率较大的因素，具体包括日最高气温、最低气温、平均气温、平均相对湿度、日照小时数、地表最高辐射强度、地表最低辐射强度和地表平均辐射强度。光伏数据预处理和聚类在R语言中进行，预测仿真在Matlab 2014a环境中进行。

5.1 光伏数据预处理分析

用傅里叶基函数将历史min级光伏出力数据展开，得到函数化序列，图5展示了五种典型场景用傅里叶基函数变换前后的对比图。

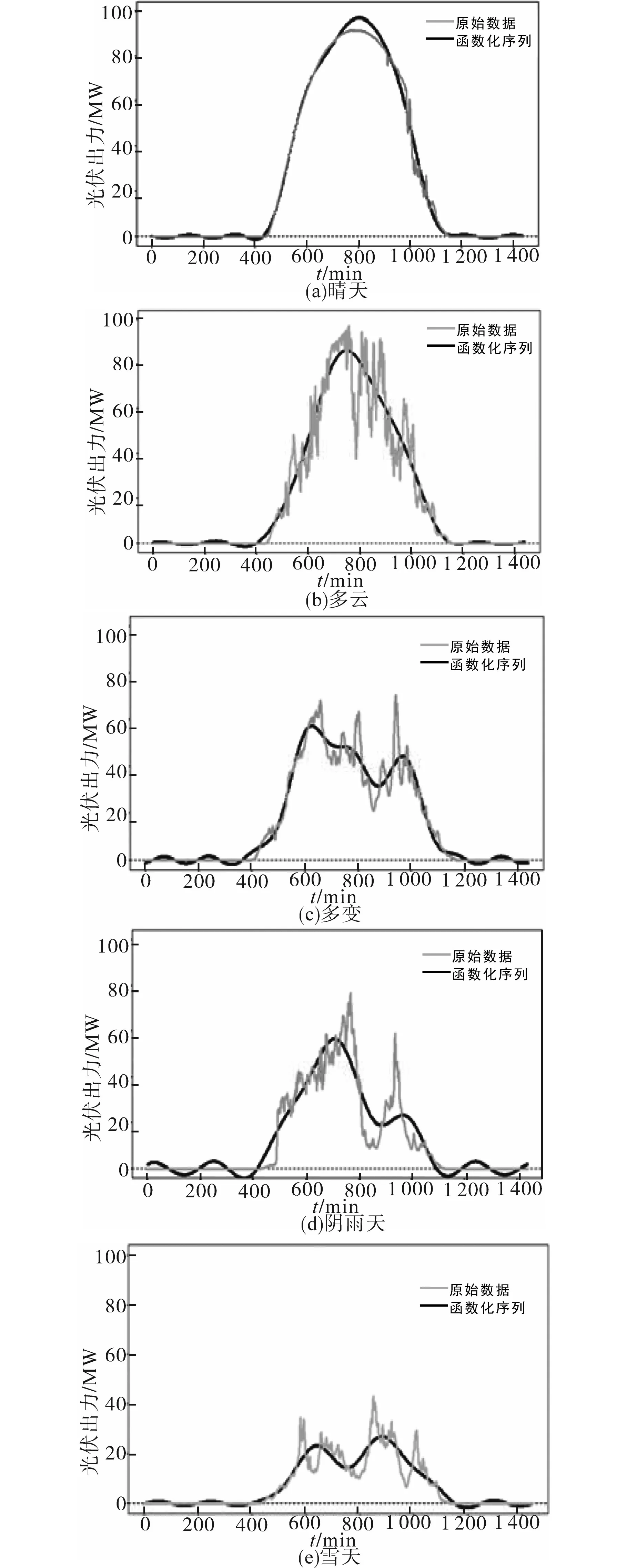
图5 典型天气下光伏原始序列与函数化序列对比图Fig.5 Comparison of photovoltaic raw sequence and functionalized sequence in typical weather

表1为主成分方差贡献率表。由表1可知，通常情况下，选取大于85%的主成分即可以满足要求，因此选取前2～4个主成分都满足要求。若对光伏函数数据提取前2个主成分，方差累计贡献率可达90.54%，但聚类效果差，如2018年2月无论晴天、雨雪全聚为一类；若只提取前三个主成分，会把2018年10月晴天和雨天聚成一类；若提取前四个，方差累计贡献率可达98.78%，聚类效果较好。

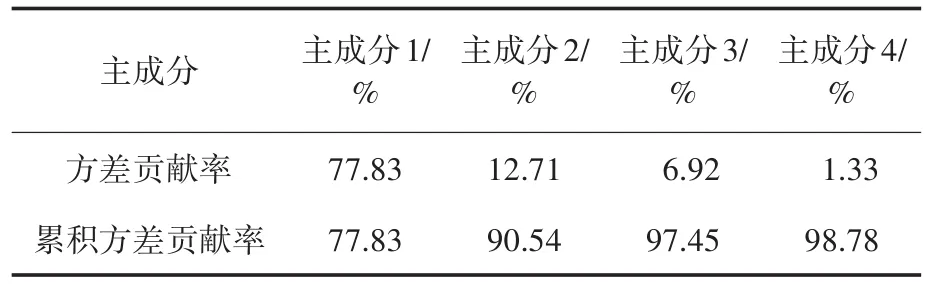
表1 主成分方差贡献率Tab.1 The contribution rate of the main component variance

5.2 基于GMM-EM算法的聚类分析

R语言中预设GMM-EM模型聚类数为1～9，基于贝叶斯信息准则（BIC）选取最优聚类个数，当BIC达到最小时，其对应的聚类数为最优聚类数[18]。

图6为基于BIC折线图。从图6可以看出最优聚类数应为5。

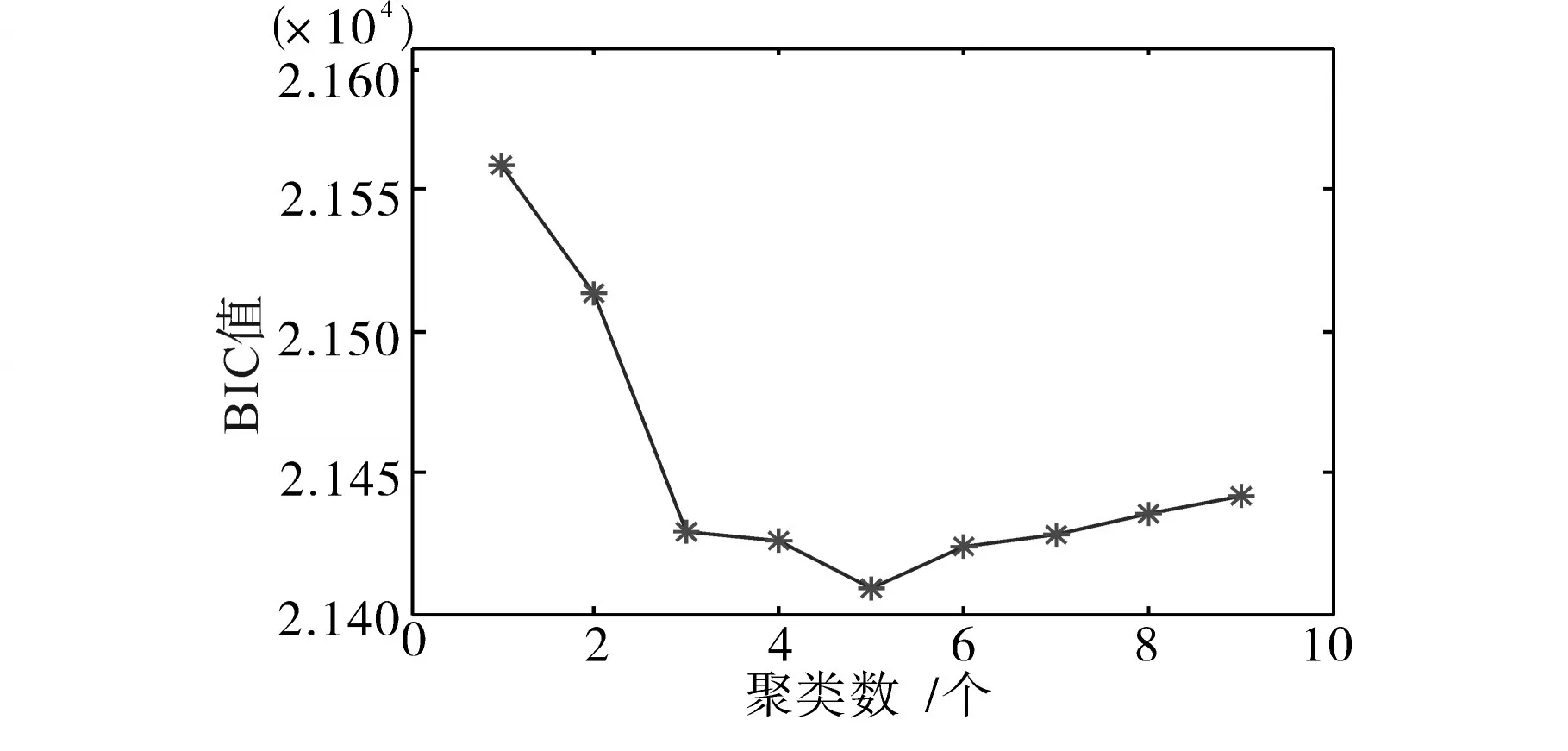
图6 基于BIC折线图Fig.6 Line chart based on BIC

表2为聚类簇和形态中心样本信息表。

表2 聚类簇和形态中心样本信息Tab.2 Clustering cluster and morphological center sample information

图7为通过GMM-EM算法对光伏主成分特征向量聚类后生成的五个类别，分别用形态中心和均值中心来突出该类别的特征，形态中心所在的日期及天气如表2所示。

图7 GMM-EM算法得到的聚类簇与形态均值中心Fig.7 Cluster cluster and morphological mean center obtained by GMM-EM algorithm

从表2和图7观察到，聚类结果层次分明，簇内形态中心有较高区分度，光伏聚类结果与天气相互映照。

5.3 基于改进PSO-ELM光伏数据预测分析

为有效改善光伏预测结果，ELM神经网络和PSO算法的重要网络参数设置如下。

5.3.1 ELM神经网络参数设置

1）ELM 所需参数[10，19]：将全天最高气温Tmax，最低气温Tmin，平均气温ˉ，地表最大辐射强度T地max，地表最小辐射强度T地min，地表平均辐射强度，平均相对湿度ˉ，日照小时数H作为 ELM神经网络的输入该天7∶00～20∶00的所有光伏出力作为输出Xij=[Xi1,Xi2,…,Xim]，m=1,2,…,M，Xij代表第i天j时刻的光伏出力。

2）ELM参数设置：采用的ELM结构为8-80-780，输入层节点数8，即ELM神经网络输入变量为天气数据；隐含层节点80是通过经验公式（13）初步确定后，再由多次ELM网络训练选取使得光伏预测出力误差最小的节点数；输出层为780节点，表示光伏min级出力，因光伏晚上不发电，本文选取7∶00～20∶00光伏min级出力数据，共780个数据。

式中：L为隐含层节点数；N，M分别为输入、输出节点数。

5.3.2 PSO算法的重要网络参数设置

PSO参数设置：粒子种群规模设置为100，迭代次数50次，惯性权重分别为ws=0.9，we=0.4，采用式（5）的减速方式；加速因子设置依据式（6）；粒子最大速度为vmax=1和最小速度为vmin=-1。

从GMM-EM聚类算法得到的聚类簇中各随机任取1 d作为测试样本，其余的样本作为改进PSO-ELM神经网络的训练样本，分别对五种典型场景预测未来1 d的光伏出力数据。为直观地验证所提模型的预测性能，分别采用ELM，PSOELM，PSO-BP（粒子群算法-BP神经网络），PSOSVM和改进PSO-ELM模型进行预测并进行均方差E、平均相对误差ˉ分析和算法耗时对比，如图8～图10以及表3所示。

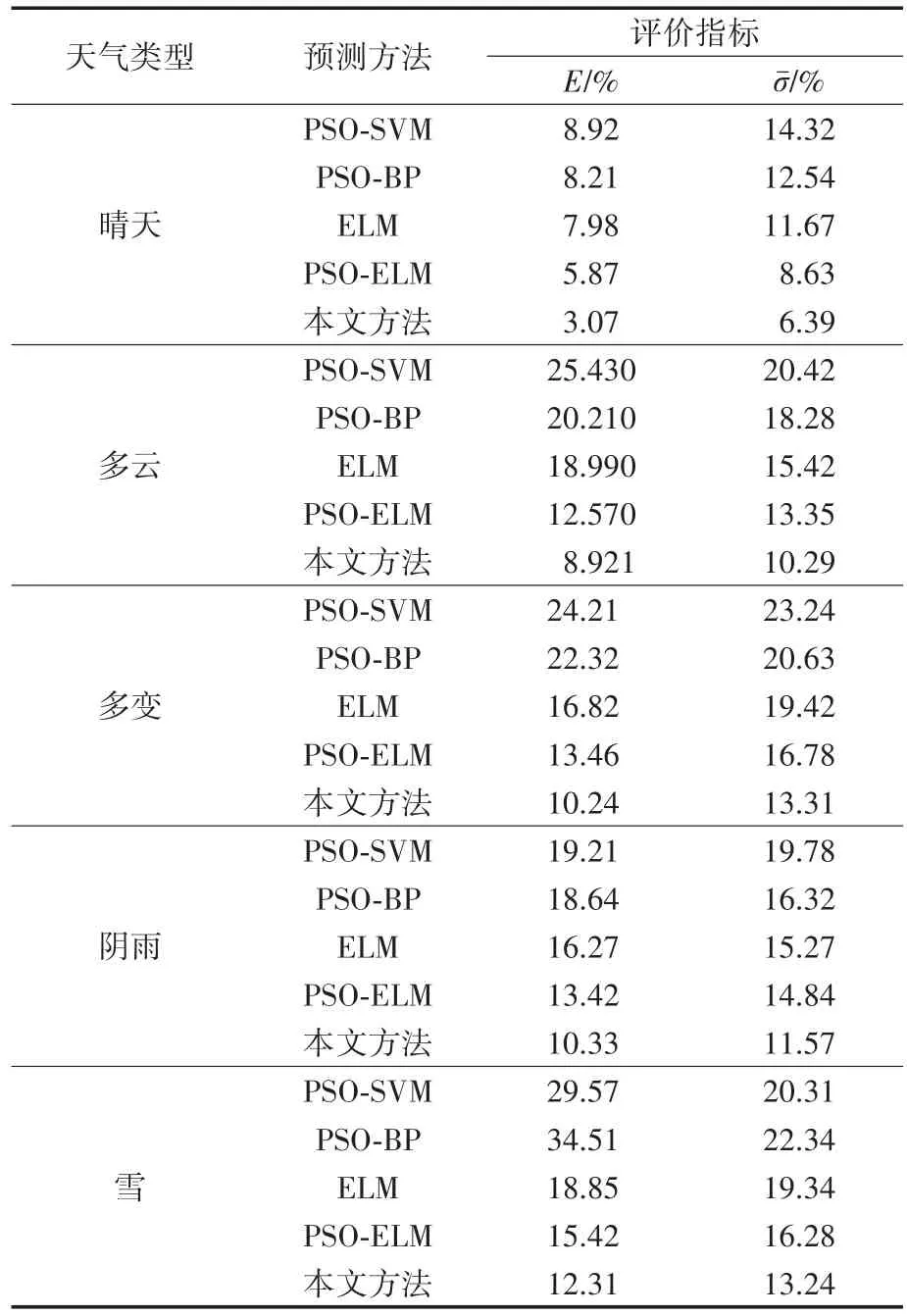
表3 测试集的误差分析Tab.3 Error analysis of test set

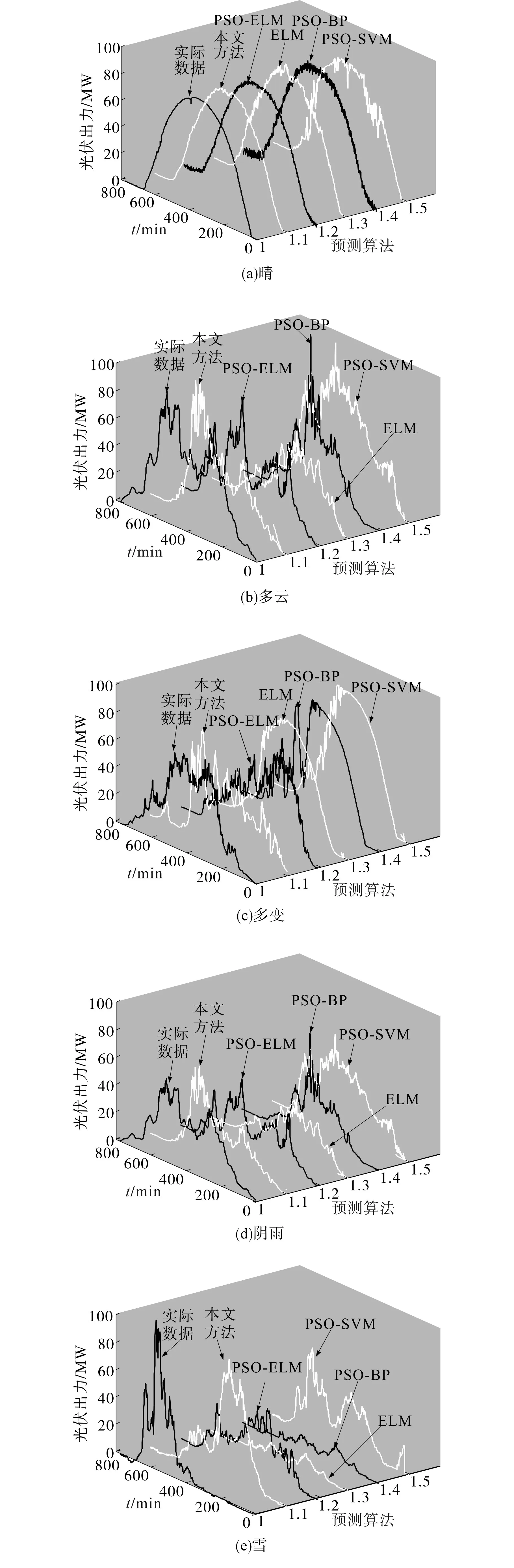
图8 三种方法预测结果对比3D展示图Fig.8 Comparison of three methods of prediction results 3D display

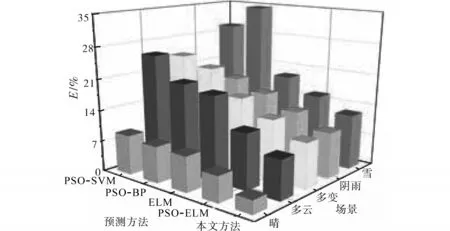
图9 不同预测算法下均方差值EFig.9 The value of mean square deviation E under different prediction algorithm

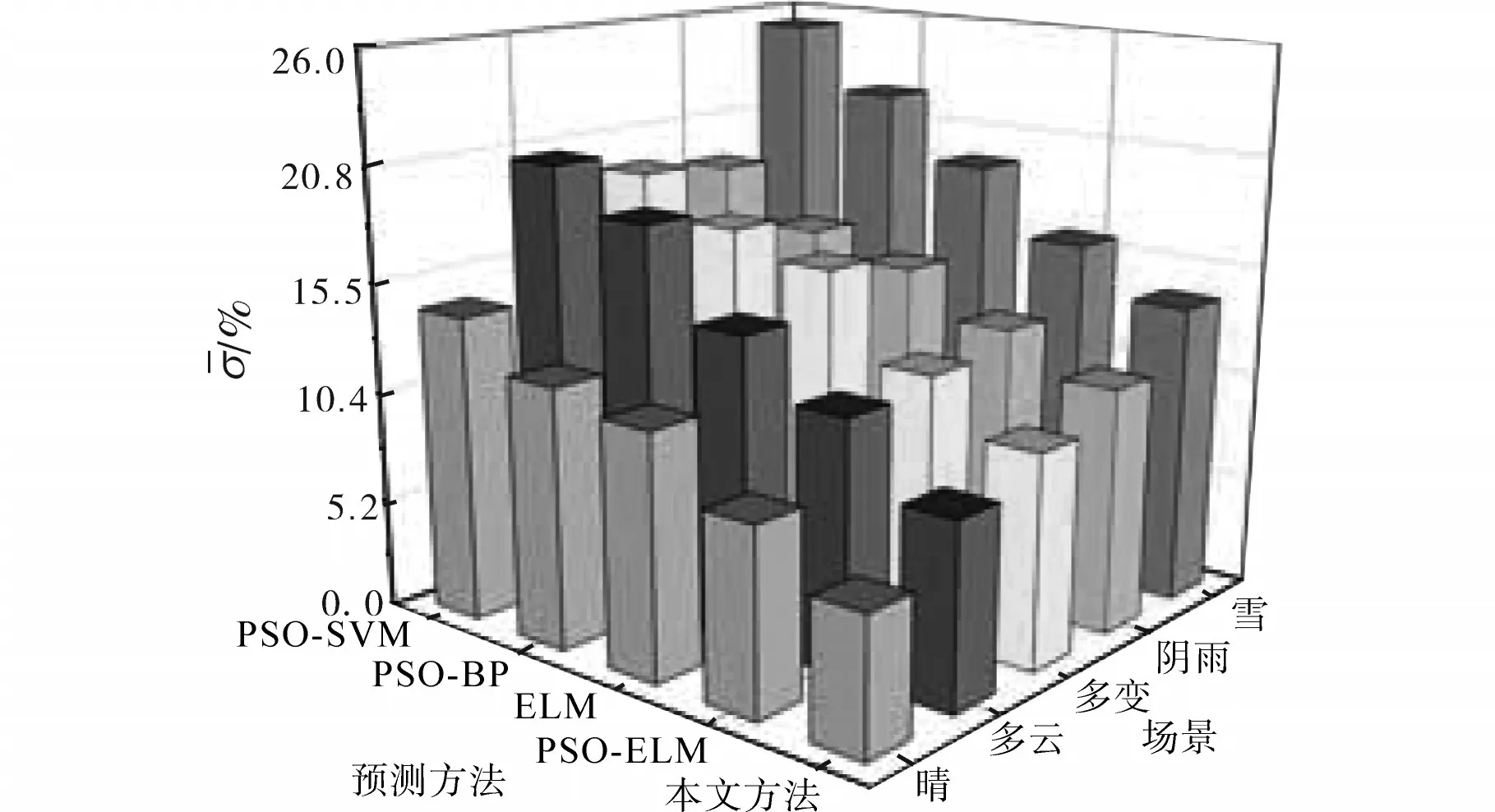
图10 不同预测算法下平均相对误差值σFig.10 Average relative error valueσunder different prediction algorithm

从图8～图10以及表3可以看出，利用改进PSO-ELM算法得到的光伏min级出力，在晴、多云、多变、阴雨和雪五种场景下，无论是平均相对误差，还是均方差，都比其余四种对比算法要小。以晴天为例，五种算法的均方差E和平均相对误差σˉ分别为3.07%，5.87%，7.98%，8.21%，8.92%和6.39%，8.63%，11.67%，12.54%，14.32%。

6 结论

本文为了研究具有函数型特征的光伏数据，通过傅里叶基函数将光伏离散数据转换为函数数据，从函数分析的角度出发，使用FPCA将函数数据降维，得到函数主成分的得分系数，提取了四个包含原信息95%以上的新变量作为聚类样本的输入，解决了因min级光伏数据维数过高，导致数据聚类复杂缓慢以及效果差等问题，消除了部分干扰数据形态的噪声信号，保留了原始序列的主要信息。使用GMM-EM算法对主成分特征向量聚类，能够快速精确对样本进行聚类，其结果图和天气信息验证表均表明聚类的有效性。

ELM模型对于大数据样本适应性较好，不仅包含了传统神经网络的优点，而且训练速度快，适用于函数型光伏数据的预测。改进PSO算法引入平均粒子距离，对不同性能的粒子动态分配惯性权重和学习因子，解决了传统PSO算法容易陷入局部最优的问题，通过改进PSO算法寻求ELM神经网络的输入层权值和隐含层阈值，提升了网络的泛化能力和稳定性。

算例分析结果表明，本文所提出的基于函数型光伏数据的预测方法，具有一定的实用价值。