基于改进强跟踪滤波器的PMSM矢量控制

孟得龙，李宁洲，卫晓娟

(兰州交通大学 机电工程学院，兰州 730070)

0 引 言

近些年来，无速度传感器控制因为运行成本低，运行性能良好，成为电机控制领域的研究热点。文献[1]模型参考自适应算法估计永磁同步电机转子位置角及转速，实现无速度传感器控制。文献[2]采用模糊超螺旋算法二阶滑模观测器，提高了转子位置估计精度，增强了控制系统的鲁棒性。扩展卡尔曼滤波算法以及改进的扩展卡尔曼滤波算法因为能够对系统状态实行在线估计，进而实现对系统的实时控制，也被广泛应用于电机控制领域[3-4]。文献[5]利用扩展卡尔曼滤波算法估计电机电流，实现了无电流传感器控制,对于电机转速及转子位置未进行研究。文献[6-8]分别采用中心差分扩展卡尔曼滤波算法、抗差扩展卡尔曼滤波算法以及改进的模糊卡尔曼滤波算法对感应电机进行转速估计，取得了良好的控制效果，提高了转速估计精度，但增加了计算过程的复杂程度。文献[9]采用低阶串行双扩展卡尔曼滤波算法，实现了永磁直线同步电机无速度传感器控制系统的设计，同样计算过程复杂。文献[10]采用平方根卡尔曼滤波算法对永磁同步电机实行无速度传感器控制，仿真效果良好。文献[11-13]采用扩展卡尔曼滤波算法估计电机转速及转子位置角，算法简单，但估计精度不高，滤波效果较差。

本文在扩展卡尔曼滤波(以下简称EKF)的基础上，采用带多重渐消因子的强跟踪扩展卡尔曼滤波算法来估计转速及转子位置，不仅提高滤波的稳定性和收敛性，而且算法相对简单，易于实现。

1 传统扩展卡尔曼滤波器算法

表贴式三相永磁同步电动机(以下简称PMSM)在静止坐标系下的电压方程[14]：

(1)

将式(1)变换为电流方程，可得：

(2)

考虑到式(3)所示关系：

(3)

由式(1)、式(2)、式(3)得到如下的状态方程：

(4)

y=Cx

(5)

式中：

(6)

(7)

(8)

将式(4)和式(5)离散化，可得：

x(k+1)=f[x(k)]+B(k)u(k)+V(k)

(9)

y(k)=C(k)x(k)+W(k)

(10)

式中：V(k)为系统噪声;W(k)为测量噪声。

传统扩展卡尔曼滤波器的状态估计可分为以下几个步骤：

(1)一步预测：

(11)

式中：Ts为采样时间;“～”表示预测值;“^”表示估计值。

(2)计算此预测对应的输出：

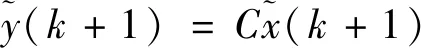
(12)

(3)计算预测协方差阵：

(13)

式中：

(14)

结果为：

(15)

(4)计算EKF的增益矩阵:

(16)

(5)计算优化状态估计值：

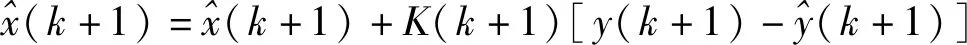
(17)

(6)计算估计误差协方差矩阵：

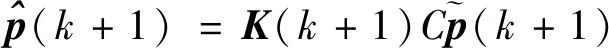
(18)

2 带多重次优渐消因子的扩展卡尔曼滤波算法[15]

由于传统卡尔曼滤波算法在对状态变量估计的过程中精度不高，有学者提出带次优渐消因子的扩展卡尔曼滤波算法。同时，为克服渐消因子易引起过调节这一问题，在算法中引入弱化因子。

根据残差序列的正交性原理，如式(19)所示。同时，定义式(20)：

(19)

(20)

式中：β≥1为弱化因子;Vk为残差协方差矩阵;Hk为观测矩阵;Q,Rk为噪声协方差矩阵。定义如下：

(21)

式中：εk为残差序列，εk=zk-zk/k-1；0<ρ≤1为遗忘因子，通常取ρ=0.95。

对式(20)两端求矩阵的迹，可以得到渐消因子λk的次优解：

(22)

式中：

(23)

式中：tr[ ]为矩阵的迹。

将式(22)代入到式(13)中，可以得到带单一次优渐消因子的状态误差协方差矩阵：

pk/k-1=λkFkpkFk+Q

(24)

由于篇幅限制，带渐消因子的卡尔曼滤波稳定性推导不再进行赘述。

系统模型的不确定性在不同状态时的影响是不同的，采用单一渐消因子时，状态跟踪性能不理想。因此，为进一步提高滤波器的强跟踪性能，本文采用带多重次优渐消因子的扩展卡尔曼滤波器(SMFEKF)。由式(24)及系统先验知识，可以大致确定：

(25)

令：

(26)

式中：αi≥1均为预先选定的常数，由先验信息确定；ck为待定因子。则可以确定多重次优渐消因子的一般算法如下：

(27)

同时，将式(25)代入式(24)可得：

(28)

总结上述推导过程，多重次优渐消因子λk求解算法如下：

(29)

由扩展卡尔曼滤波算法结合，式(25)～式(29)便可以得到SMFEKF算法。至此，SMFEKF算法所需参数以及公式全部给出。

图1为基于SMFEKF的PMSM磁场定向控制仿真框图。图2为SMFEKF模块。

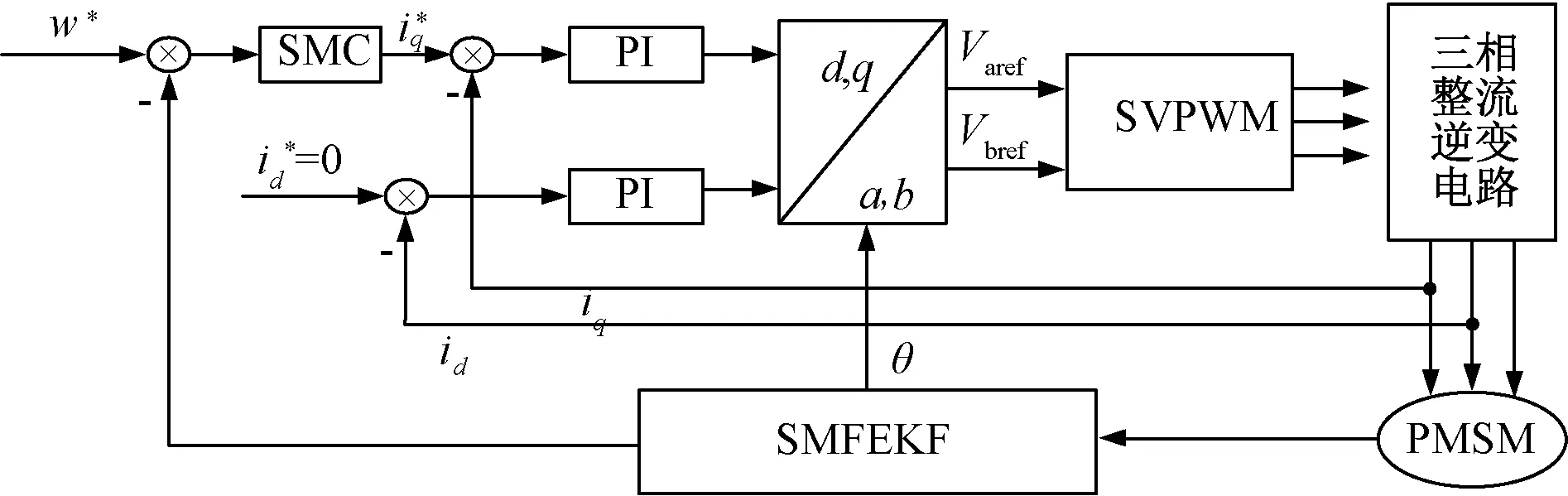
图1 基于SMFEKF的PMSM磁场定向控制仿真框图

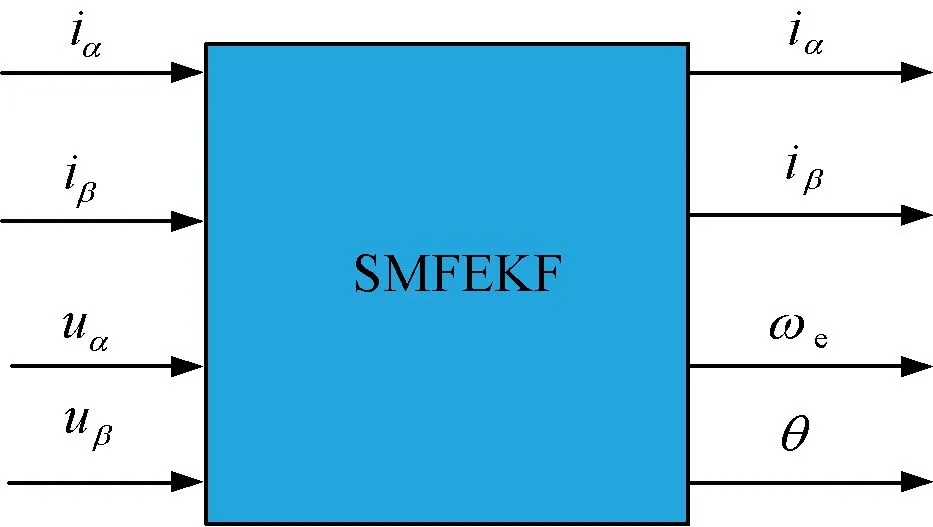
图2 SMFEKF算法框图

3 仿真结果

仿真用到的PMSM主要参数：Rs=2.875 Ω；Ld=8.5 mH；Lq=8.5 mH；φf=0.175 Wb；J=0.003 kg·m2；p=4；系统仿真时间t=0.4 s；给定速度为1 000 r/min；在起动0.1 s后给定负载转矩15 N·m。仿真结果如图3～图6所示。

由图3可知,SMFEKF矢量控制相比传统扩展卡尔曼算法(EKF)，在转矩输出方面，脉动成分降低，稳态性能良好。在0.1 s突加负载时，转矩的响应速度较快，上升比较平稳。

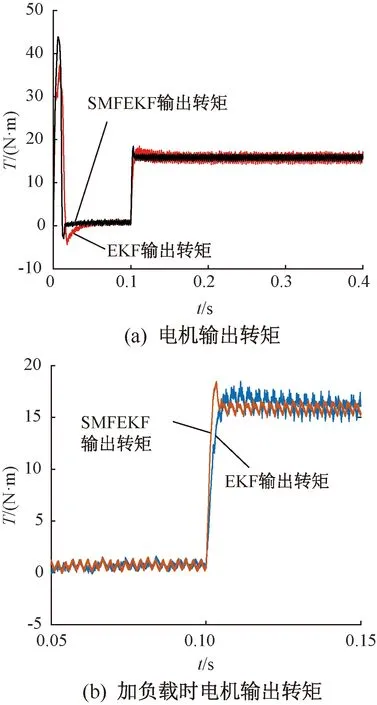
图3 电机转矩

由图4可知,电机输出转速响应较快，转速估计未出现超调现象，动态响应效果明显改善。在0.1 s施加负载转矩时，转速出现小幅下降，但很快达到给定转速，并稳定运行。从图4(b)可知，基于SMFEKF的转速差在电机起动阶段，超调量大幅降低，并最终稳定在零值附近。

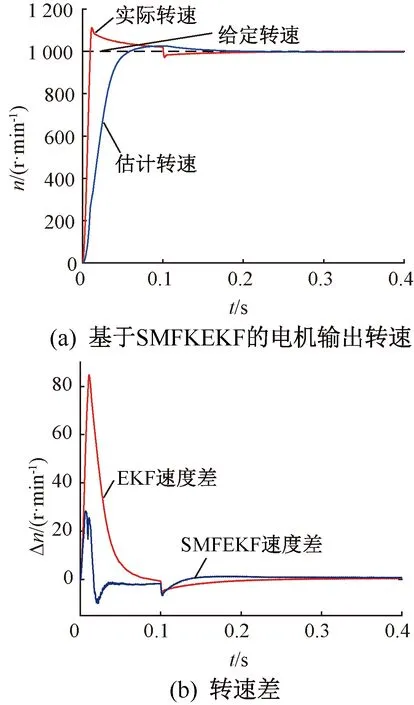
图4 电机转速及转速差

由图5可知，估计的转子位置角能够准确追踪电机实际转子位置角，在0.1～0.4 s电机稳定运行阶段，基于SMFEKF估计误差明显小于EKF估计误差，在一定程度上提高了无位置传感器控制的运行性能。图6为电机α轴定子电流。

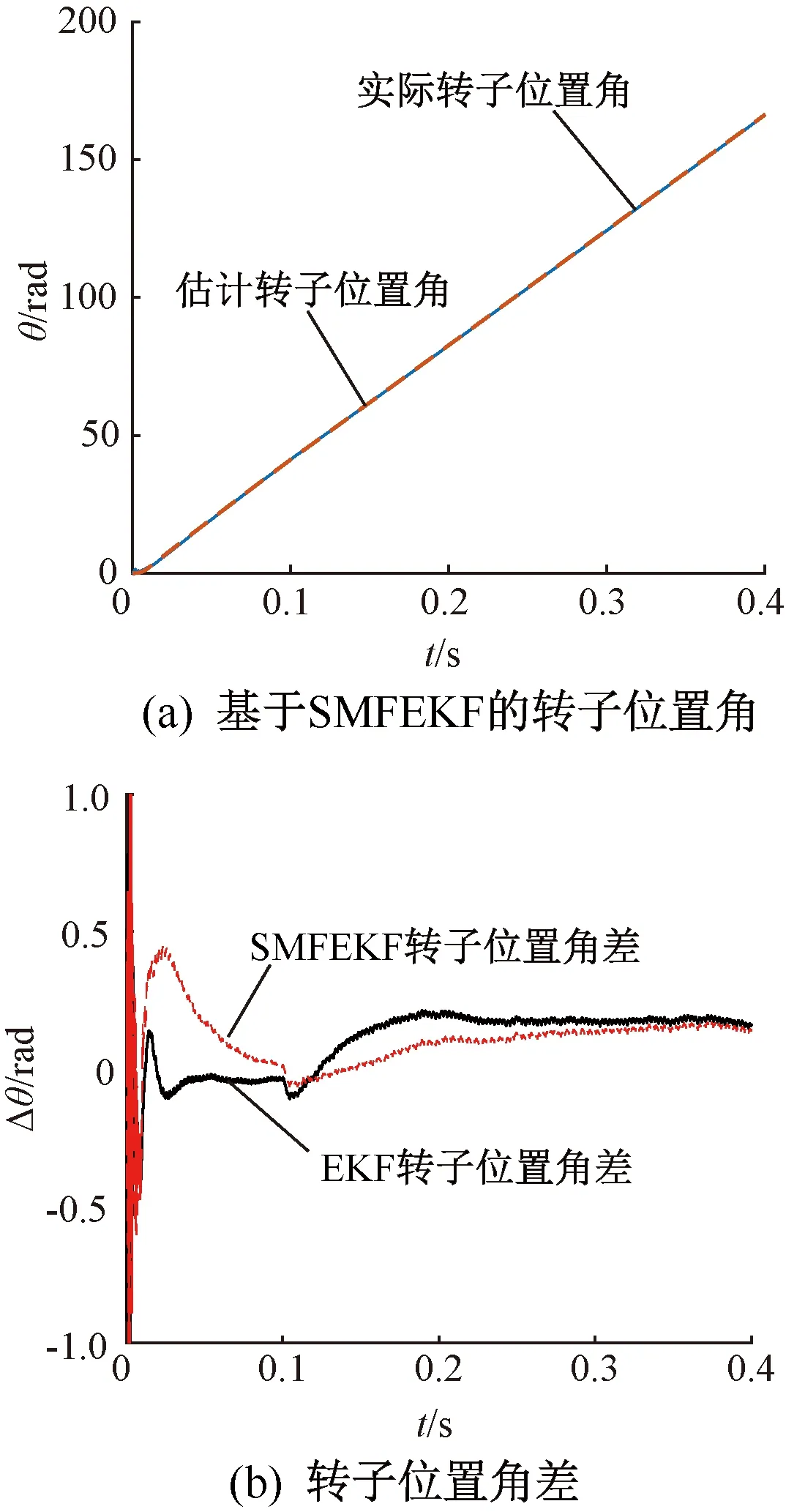
图5 电机输出转子位置角

从图6中可以看出，估计电流能够较好地跟踪实际电流，且电流波形具有较高的正弦度，未出现明显畸变。

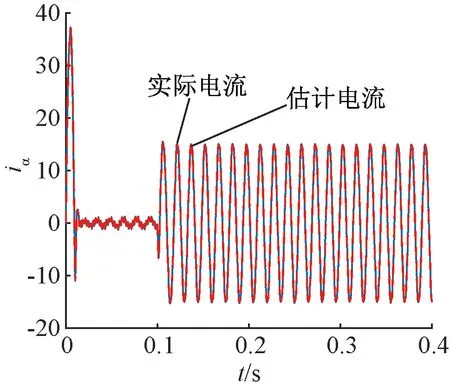
图6 α轴定子电流

4 结 语

本文在 PMSM两相静止坐标系数学模型基础上，设计基于SMFEKF的无速度传感器矢量控制系统。仿真结果表明:该系统不仅能够准确估计出转子空间位置和转速，同时减少了电机输出转矩的脉动成分，具有良好的运行性能。由于PMSM是一个多变量、强非线性的系统，通过辨识系统参数来提高转速估计精度和增强系统鲁棒性还需在后续工作中作进一步研究。