渐开线斜齿轮齿面点偏差求解及三维齿面偏差评定
张登攀,王黎阳,张洪良,刘瑞弢,王宇,姚新景
(河南理工大学 机械与动力工程学院,河南 焦作 454000)
0 引 言
近年来,随着坐标测量技术、传感器技术和计算机技术的发展,尤其是数据处理软件功能的增强,三维齿面形貌偏差、分解齿轮单项几何偏差和频谱分析等误差项目的测量得到了推广[1]。
国内外专家学者对齿面三维偏差获取与分解开展了大量的研究。石照耀等[2]提出了多自由度回归齿面的齿轮误差评定算法;张白等[3]将齿轮三维数据降维至二维数据,再对二维测量数据进行各项误差评定;大连理工大学精密齿轮团队[4-5]对改进后的齿轮测量中心Mahr891E螺旋线偏差测量系统测量不确定度进行评定,借助Mahr891E齿轮测量中心获得齿面偏差并对齿轮三维齿面偏差拟合分离;姬建钢等[6]对渐开线圆柱齿轮修型原理及修形技术进行了综合论述;W.Lotze等[7]通过对齿面坐标拟合,提出齿轮误差三维测量技术;YUE P等[8]利用二维切比雪夫正交多项式对齿面偏差整体拟合,对齿面偏差进行评价;Vit Zeleny等[9]使用齿轮几何方法推导测点的齿形和螺旋偏差的计算公式。以上研究可以较好描述齿面偏差,但仍存在以下问题:齿面点偏差的求解过程不明确;三维齿面偏差曲面拟合评价与传统齿面偏差评价的关系不确定。
针对以上问题,本文提出一种利用坐标法获取三维齿面偏差的方法。在柱坐标系下推导圆柱渐开线斜齿轮测量点坐标与标准齿面的垂直偏差,使用二维勒让德正交多项式对齿面偏差整体拟合并评定齿面偏差。以含有径向变位的6级精度圆柱斜齿轮为例,采用三坐标测量机对齿轮进行测量实验,实验所得数据使用MATLAB编程计算结果,评定齿面偏差,将计算结果与齿轮测量中心报告中部分偏差数据进行对比,以验证该方法的可行性。
1 齿面点偏差的求解
本文将齿面各偏差均视为在标准齿形上偏转一定角度所形成。以齿轮上端面为基准面,把与被测齿轮齿数、模数相同的标准渐开线齿轮第一个轮齿齿形作为基准齿形,将测量点旋转变换至基准齿形附近。视测量点为偏离基准齿形一角度的辅助渐开线上一点,测量点的渐开线生成线与基准齿面渐开线的交点即为测量点端面对应点。由渐开线性质求得两者距离,其在齿面的法向分量即为垂直于齿面的偏差。
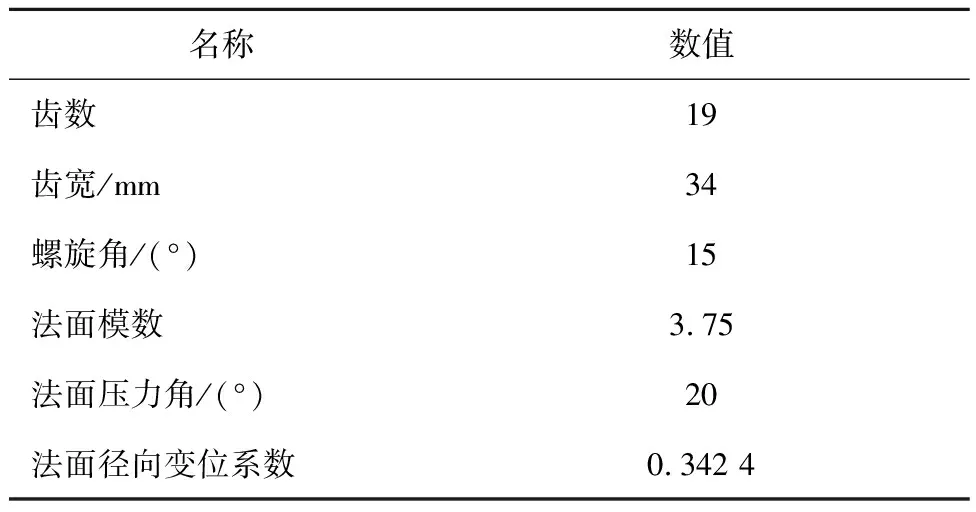
齿轮基本参数如表1示,其中螺旋角β左旋为正,右旋为负,直齿取0。
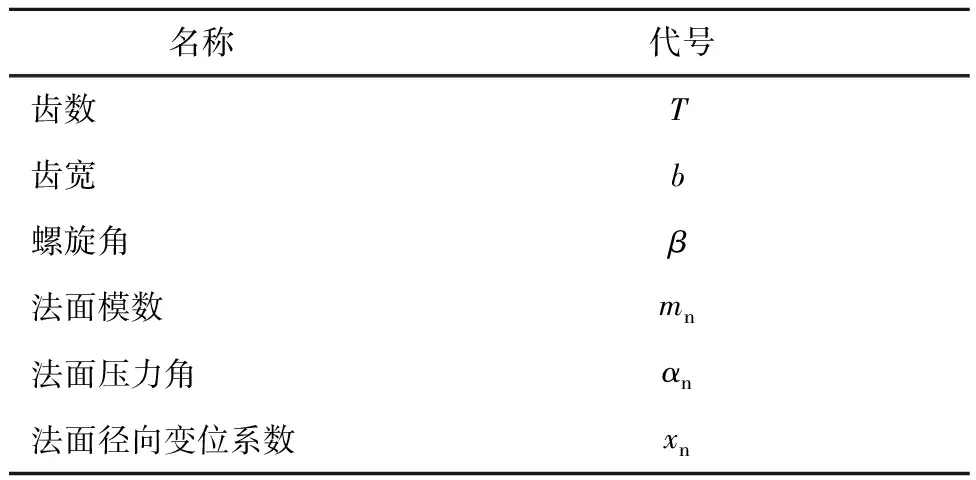
表1 斜齿轮基本参数
1.1 建立坐标系
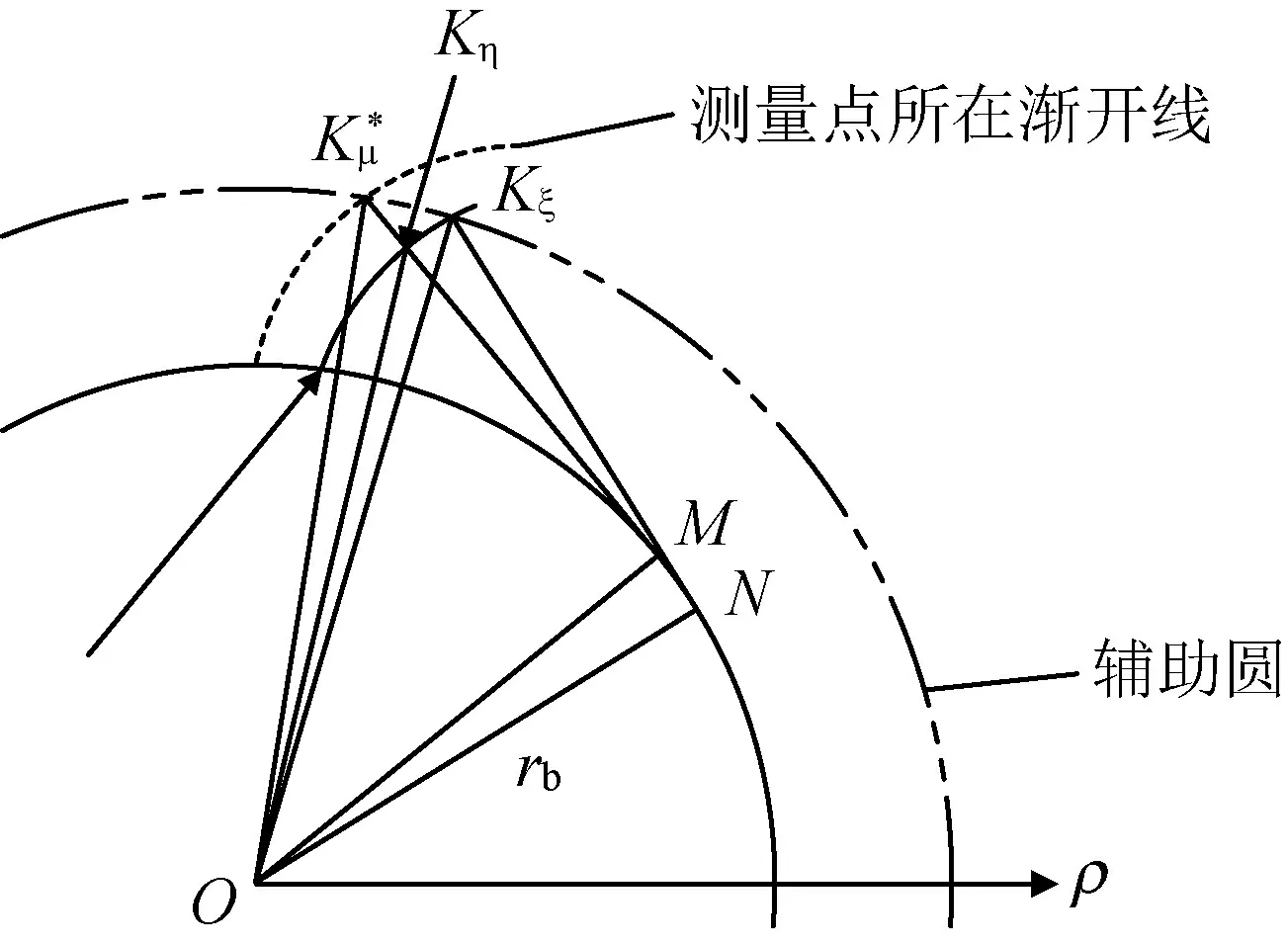
将齿轮水平放置,齿轮中心轴线向上为z轴正向,交齿轮上端面于坐标原点O。以z=0作为基准面,从原点过一齿顶圆弧中点向外引出一条极轴ρ,并以该齿为基准作为第一齿,从第一齿顺时针顺序编号[10],逆时针为极角正向,建立齿轮柱坐标系,如图1所示。此坐标系是依据测量直角坐标系经变换得到的计算柱坐标系。
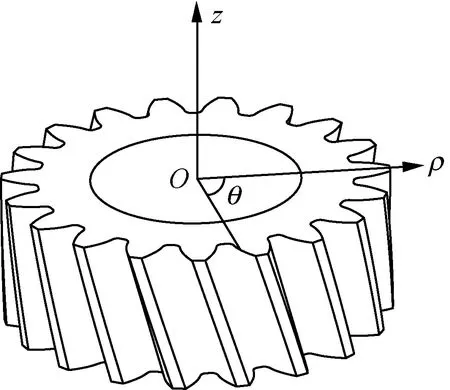
图1 齿轮柱坐标系
选取被测齿面上取值范围内任一测量点Kμ(ρμ,θμ,zμ)为例。其中下标μ表示该点为测量点,以与η表示基准齿形点相区别。表2列出本文涉及到的斜齿圆柱齿轮参数及计算公式,本文取法面齿顶高系数为1,法面顶隙系数为0.25。

表2 斜齿圆柱齿轮参数及计算公式
首先将测量点坐标值转换为柱坐标值,针对渐开线部分给出取值范围以筛选数据。
由表2得(Te为当rb=rf时齿轮齿数)
(1)
极径ρμ的取值:当齿数T≤Te时,齿根圆半径小于基圆半径,rb<ρμ zμ的取值为:-b 斜齿圆柱齿轮可以看作由渐开线标准齿形沿轴向螺旋上升形成,利用该性质将测量点Kμ旋转至z=0基准面,对应旋转角度如图2示。 图2 螺旋角在基准面对应角度 由螺旋角与直径关系[11],Kμ旋转到z=0端面后极角θd如式(2)表示,其中βμ为Kμ处螺旋角。 通过式(3)求出该测量点位于第i齿,其中方括号表示向下取整: (3) 将θd去除i-1个齿距的影响,得到在基准齿形附近的θt: θt=θd-(i-1)×π×mt, (4) 以测量点Kμ极径ρμ为半径在基准面做辅助圆,交第一基准齿形于辅助点Kξ(ρξ,θξ,0),如图3所示。 图3 基准齿形各角度 Kξ点处的极径ρξ=ρμ,根据渐开线极坐标方程[12],其压力角αξ与渐开线函数uξ分别为 (5) uξ=tanαξ-αξ, (6) 分度圆压力角对应的渐开线函数为 uα=tanαt-αt, (7) 在标准齿形分度圆上齿厚等于齿槽宽,半个齿厚圆弧对应极角为 λ=2π/4T, (8) 斜齿圆柱齿轮传动多采用标准斜齿轮,也可以采用高度变位或角度变位。采用角度变位对提高斜齿轮的承载能力效果不大,本文对高度变位齿轮给出计算。 高度变位又名等移距变位,可将变位视为基准齿形沿渐开线方向、齿顶齿根沿径向偏移2xn×mn,如图4所示。对于变位斜齿圆柱齿轮,如果用其端面的值,则仍可用直齿圆柱齿轮的计算公式。渐开线齿廓端面变位量px为 定向越野运动并不像传统体育教学只依赖固定的运动场地,而是充分利用天然的运动场地,例如郊外、田野或校园内的小树林。充分利用天然的运动场地让体育教学内涵变得更加丰富多彩。大学生的课余时间相对来说较为充裕,适当开展定向越野运动能让学生走出寝室,丰富课余生活。 图4 端面径向变位量 px=xn×cosβ×mt×tanαt。 (9) 图5 端面点偏差 通过以上计算,得出测量点垂直于端面基准齿形的距离,空间中测量点垂直于齿面的距离[13]为(βb为基圆螺旋角) dμ=dt×cosβb。 (11) 对齿面所有测量点进行计算,形成齿面偏差点云,建立齿面坐标系,对齿面偏差点云进行拟合评估,从而实现对三维齿面偏差的评定。 参照GB/T 10095.1-2008中的齿廓偏差和螺旋线偏差范围,建立齿面(u,v,d)坐标系,如图6所示。其中,u为齿廓偏差定义中的可用长度,即2条端面基圆切线长度之差,方向沿齿廓从rb到齿顶;v为螺旋线偏差定义中的迹线长度,与齿宽成正比,方向从负齿宽到z=0;dμ为式(11)求得的齿面偏差值,方向垂直于齿面。通过式(12)计算测量点在齿面坐标对应值。 图6 齿面坐标系Fig.6 Tooth surface coordinate system (12) 二维勒让德正交多项式的正交性使各项之间无串扰,增加或删除一个项对其他项没有影响,而且由于二维勒让德正交多项式前6项函数图像与齿面常见偏差有相似特征[14],因此,齿面常见偏差可用二维勒让德多项式前6项表示。以下通过一维勒让德正交多项式引入二维勒让德正交多项式的概念。 区间为[-1,1],权函数为1,一维勒让德多项式递推表达式为 (13) 在区间x×y=[-1,1]×[-1,1]上,二维勒让德多项式表达式为(下标m,n分别为x,y的次数) Lm,n(x,y)=Pm(x)×Pn(y), (14) 由一维勒让德正交多项式的正交性: 二维勒让德正交多项式前6项表示为 (17) 取二维勒让德正交多项式前6项为基函数,对齿面偏差函数D(x,y)进行最小二乘拟合[15-16],得到D(x,y),可表示为 D(x,y)=∑Am,n×Lm,n(x,y)= (18) 在齿面坐标系下对齿面偏差点云进行拟合,齿面偏差拟合前使用3δ准则除去坏点。将u,v归一化至[-1,1]×[-1,1]区间,D即为dμ齿面偏差矩阵,代入式(19),求得各项系数: (19) 常见齿面偏差类型(齿距偏差、齿廓斜率偏差、螺旋线斜率偏差、扭曲偏差、齿廓凸度、轮齿鼓度)示意图与二维勒让德正交多项式前6项(以x,y,z为例),在[-1,1]×[-1,1]域内函数图像对比见图7。 图7 齿面偏差与二维勒让德多项式各项函数 结合GB/T 10095.1-2008与GB/Z 18620.1-2008中各偏差量计算方法与二维勒让德正交多项式前6项函数性质可推导出:拟合项中一次项L0,1,L1,0斜率为1,可用系数直接表示对应偏差量;拟合项中二次项L2,0,L0,2在域内的z范围为[-0.5,1],可用其系数值的1.5倍表示对应偏差值,其符号取决于左右齿面及偏差凹凸类型,若左齿面凸偏差、右齿面凹偏差,二次项系数符号为负,否则为正。 本文使用海克斯康GLOBAL STATUS 9128三坐标测量机,允许误差2.2+4.0L/1 000 μm(L为测量值),在规定测量环境下[18]进行齿轮测量,测量设备及环境如图8所示。 图8 齿轮测量设备及环境 被测齿轮基本参数见表3。 表3 被测齿轮基本参数 建立齿轮测量坐标,使用PC-DMIS测量软件对被测齿轮第一、五2齿左右齿面进行测量,每一齿面沿齿廓方向等距开线扫描15条线得到齿面坐标点数据,如图9所示。 图9 扫描测量获取齿面数据 通过MATLAB编程读取齿面扫描数据,分别存入x,y,z矩阵,将各矩阵转换为柱坐标对应值,通过本文算法得出齿面点云偏差,并使用二维勒让德正交多项式前6项对各齿面偏差拟合。 表4为各齿面偏差使用二维勒让德多项式拟合各项系数的计算结果,其中u′、v′为齿面坐标u、v归一化至[-1,1]表示,表中“1左”表示被测第一齿左齿面,以此类推。表5为3906型齿轮测量中心报告部分偏差数值。 表4 各齿面偏差拟合项系数 表5 3906型齿轮测量中心报告部分偏差数值 使用二维勒让德正交多项式拟合各偏差曲面如图10示。拟合项中一次项L1,0=u′与L0,1=v′系数分别对应测量中心报告中齿廓斜率偏差、螺旋线斜率偏差,系数值均在精度等级范围内。v′均值与报告中螺旋线斜率偏差均值相差较大,但其均值与三坐标测量机PC-DMISGear软件测量评估结果均值接近,初步判断是由齿轮上端面与齿轮制造基准孔存在垂直度偏差、建立测量坐标系坐标轴与理想坐标轴之间存在偏角而导致测量误差引起的。 图10 齿面偏差拟合图Fig.10 Tooth surface deviation fitting diagram 其二次项L2,0=(3×u′2-1)/2、L0,2=(3×v′2-1)/2为凹函数,分别对应测量中心报告中齿廓凸度、轮齿鼓度,本文规定逆时针方向为正,左齿面正偏差图像上凸,所以其对应二次项系数为负值。各齿面二次项系数的1.5倍分别为L2,0:-1.036(左齿面)、-1.079(右齿面);L0,2:-20.88(左齿面)、14.378(右齿面),与测量中心报告中对应项接近,验证了上文的推断。 由u′×v′混合项得出各齿面还存在一定的扭曲偏差,传统测量中心报告中无此项。齿距偏差与二维勒让德正交多项式常数项的关系的确定,需要加强实验条件,在进一步工作中完成。 (1)基于坐标法,利用渐开线基本性质,将齿面各变化均视为在标准齿形上偏转一定角度形成,推导出含有径向变位渐开线斜齿圆柱齿轮齿面点偏差的求解方法。 (2)利用二维勒让德正交多项式的正交性及其前6项与齿面偏差函数特征的相似性,对齿面偏差点云进行拟合,用拟合项描述齿廓斜率偏差、螺旋线斜率偏差、齿廓凸度和轮齿鼓度,确定勒让德正交多项式项系数与对应类型齿面偏差量的比例关系,实现了基于面偏差数据的三维齿面偏差评定。 (3)使用三坐标测量机对6级精度含有径向变位的斜齿圆柱齿轮进行测量实验,将实验结果与齿轮测量中心报告数据对比,采用以上方法实现的三维齿面偏差与测量中心报告结果接近,从而验证了该方法的可行性。 (4)确定齿距偏差项与二维勒让德常数项的关系尚需加强实验条件,以进一步验证本文结论。1.2 测量点的旋转变换
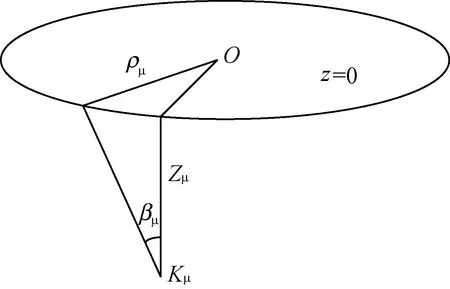
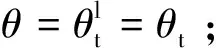
1.3 辅助点极角
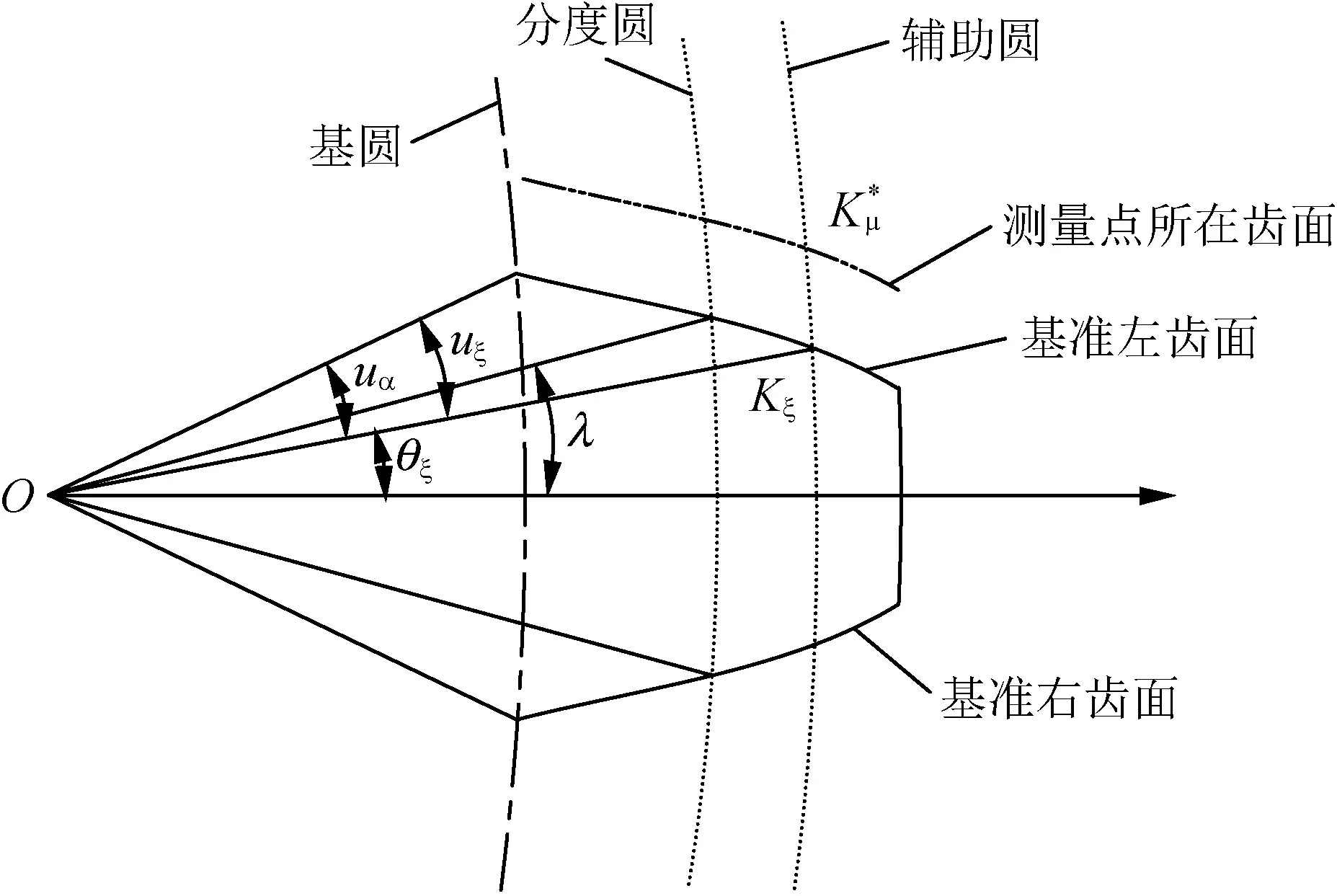
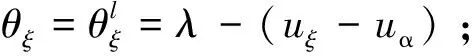
1.4 径向变位量
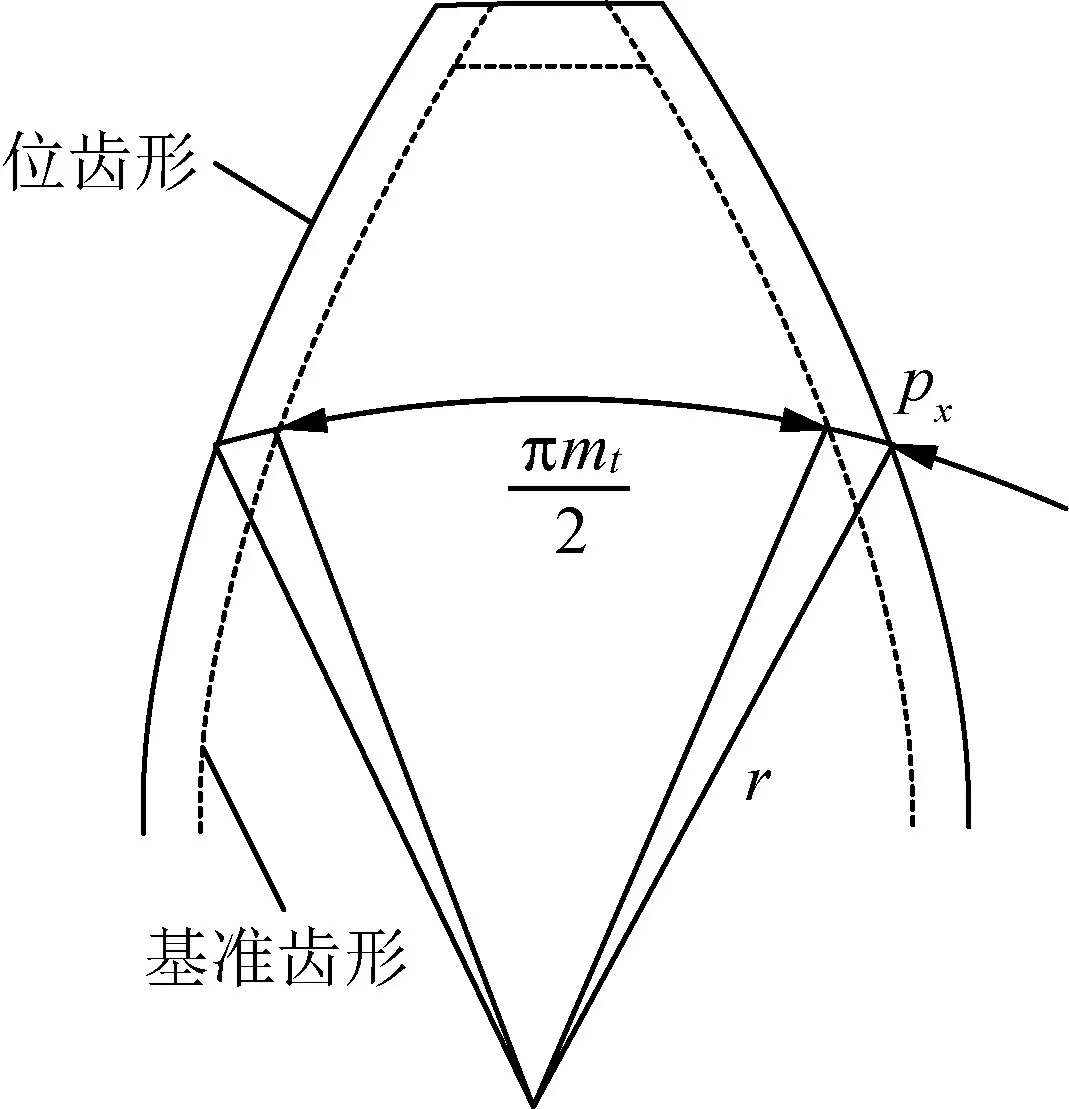
1.5 齿面点偏差的计算
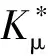
2 三维齿面偏差的评定
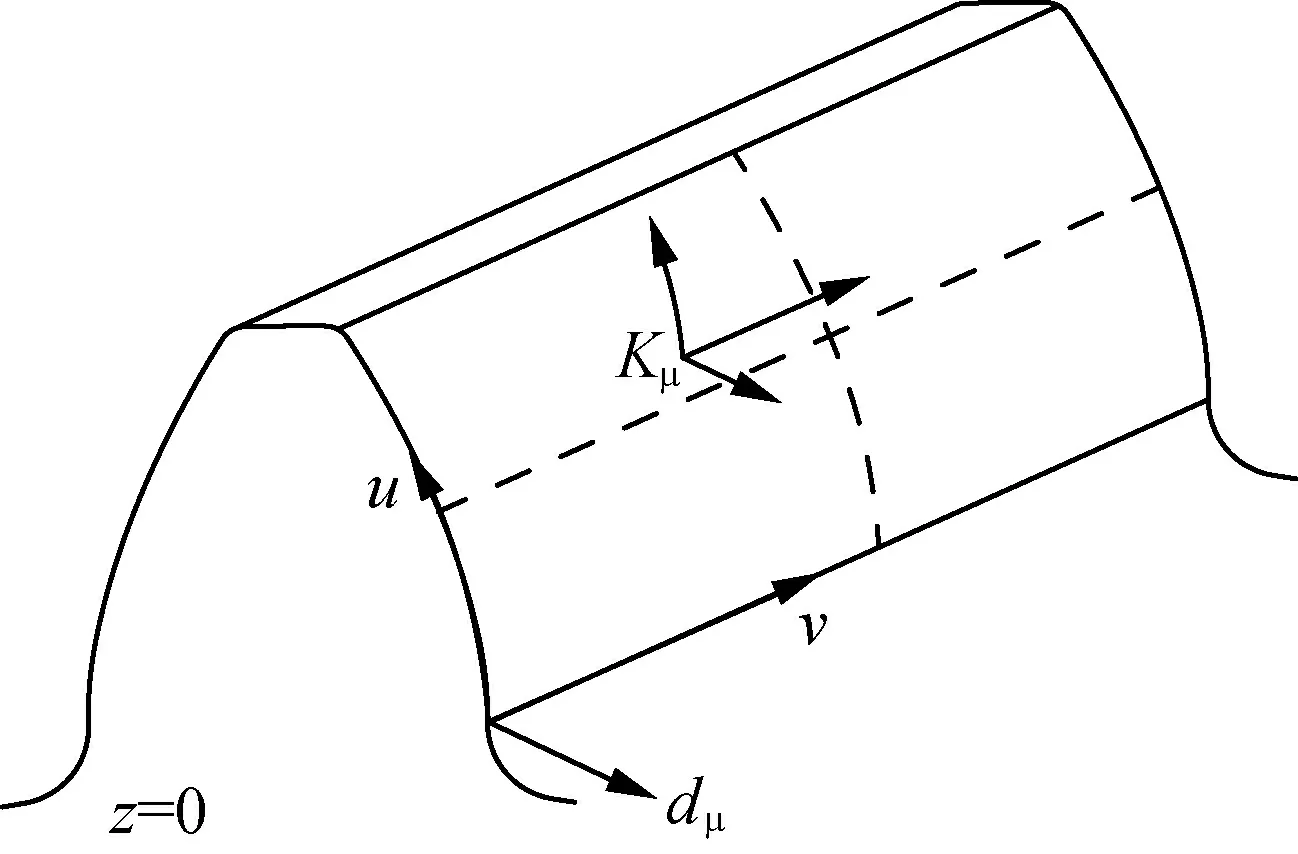
2.1 齿面坐标系建立
2.2 二维勒让德正交多项式
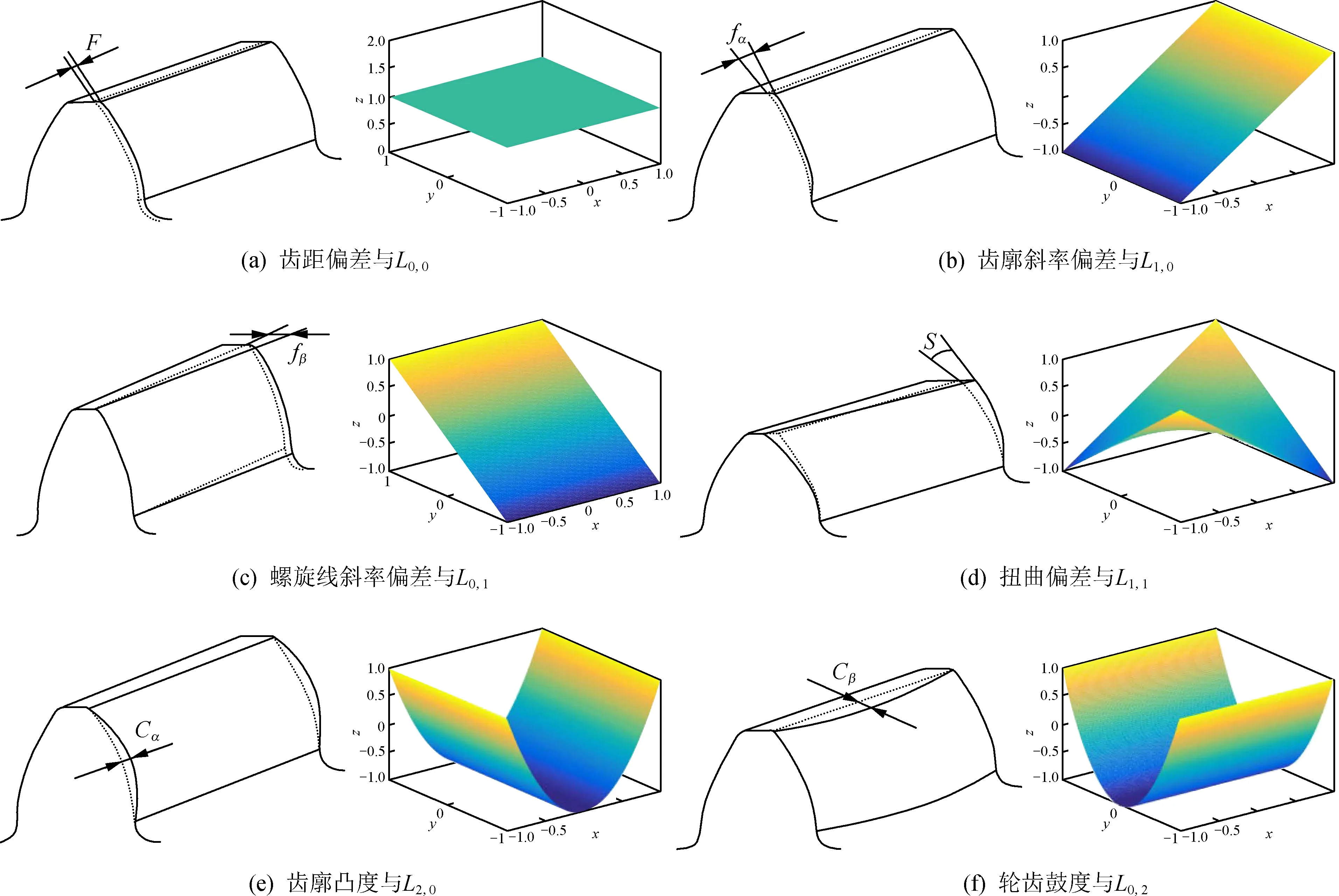
∑Am,n×Pm(x)×Pn(y)。2.3 齿面偏差评定
3 三坐标测量与齿面偏差估算


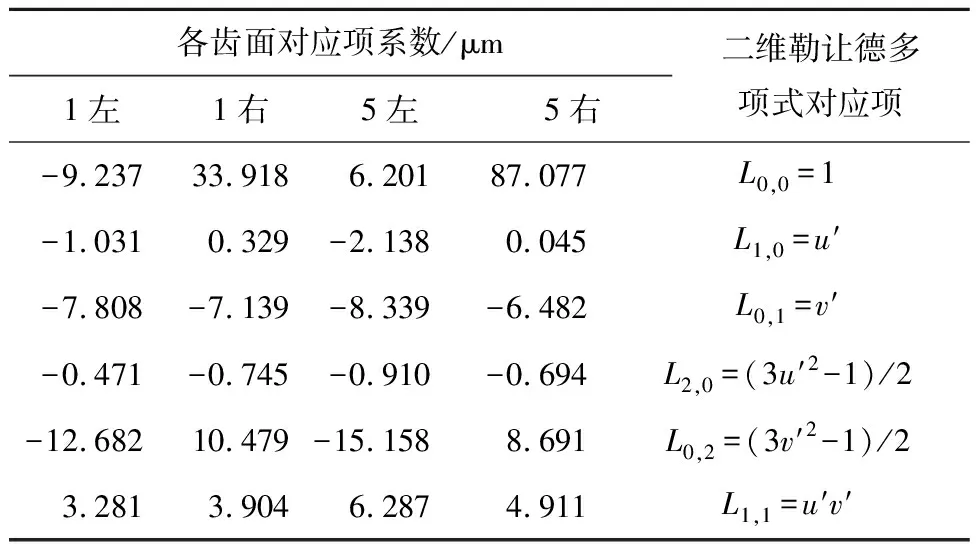

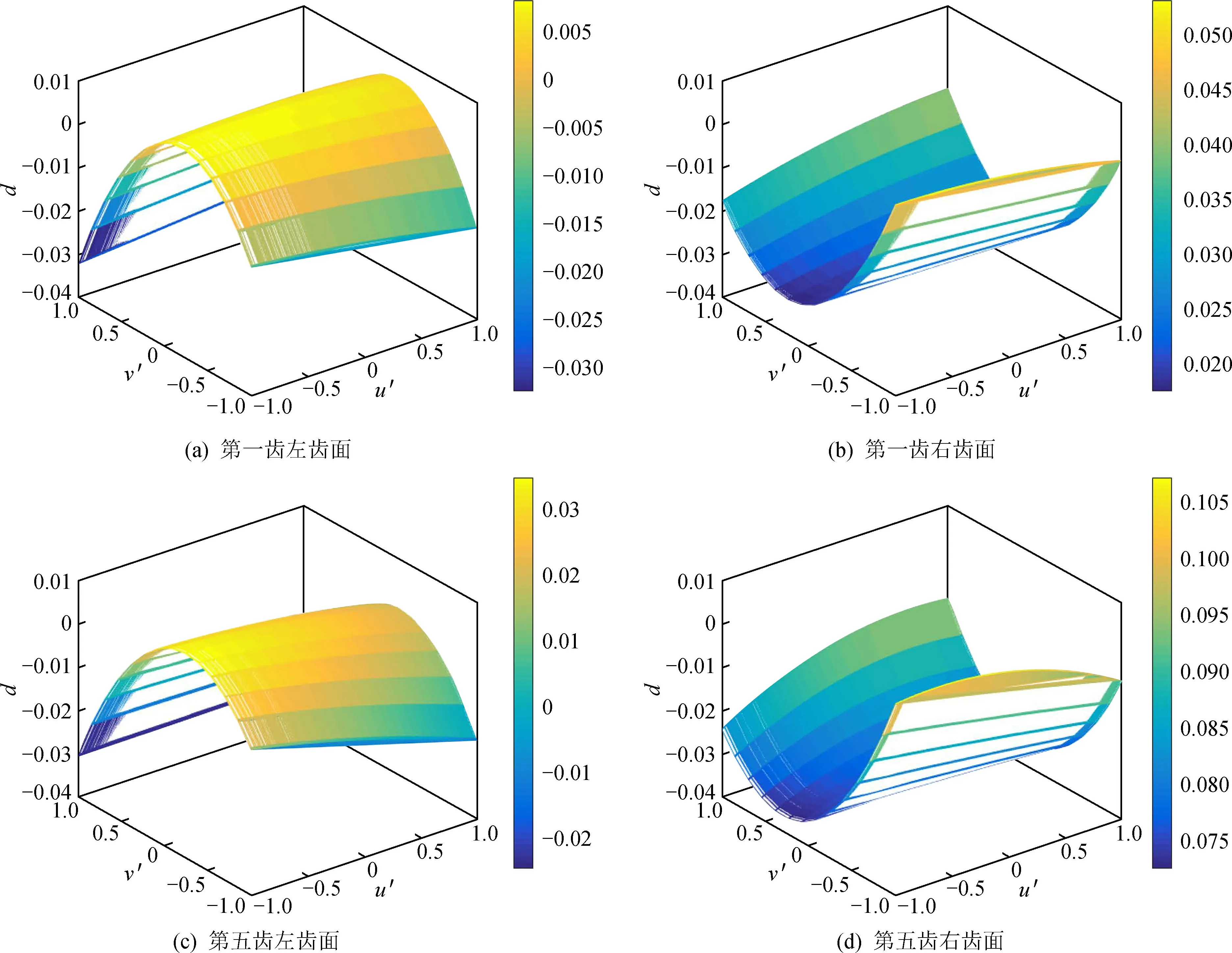
4 结 论

