Equilibrium mercury and lead isotope fractionation caused by nuclear volume effects in crystals
Sha Yang·Yun Liu
Abstract To investigate equilibrium mercury(Hg)and lead(Pb)isotope fractionation caused by the nuclear volume effect(NVE)in crystals,the electron densities at nuclei(i.e.,|Ψ(0)|2)for Hg-or Pb-bearing crystalline compounds were investigated by using the relativistic spin orbit zeroth-order regular approximation(ZORA)method with a three-dimensional periodic boundary condition based on the density functional theory(DFT).Many isotope fractionation factors of crystalline compounds are provided for the first time.Our results show,even at 1000 °C,NVE-driven Hg and Pb isotope fractionation are meaningfully large,i.e.,range from 0.12‰ to 0.49‰(202Hg/198Hg),from-0.20‰to 0.17‰(208Pb/206Pb)and from-0.08‰ to 0.06‰(207Pb/206Pb)relative to Hg0 vapor and Pb0 vapor,respectively.Specifically,the fractionations range from-0.06‰to-0.20‰(208Pb/206Pb)and from-0.02‰ to-0.08‰(207Pb/206Pb)for Pb2+-bearing species,from 0.10‰ to 0.17‰(208Pb/206Pb)and from 0.04‰ to 0.06‰(207Pb/206Pb)for Pb4+-bearing species in crystals.All calculated Hg-bearing species in crystals will enrich heavier isotope(202Hg)relative to Hg0 vapor.Meanwhile,Pb4+-bearing species enrich heavier Pb isotopes(208Pb and 207Pb)than Pb2+-bearing species in crystals,which the enrichment can be up to 0.37‰(208-Pb/206Pb)and 0.14‰(207Pb/206Pb)at 1000 °C,due to their NVEs are in opposite directions.The NVE-driven MIFs of Hg isotopes,which are compared to the Hg202-Hg198 baseline,are up to-0.158‰(),-0.024‰()and-0.094‰()relative to Hg0 vapor at 500 °C.For all studied Hg-bearing species in crystals,the MIFs of two odd-mass isotopes(i.e., and)will be changed proportionally and their ratio(i.e.,will be a constant 1.67.The NVE can also cause mass-independent fractionations for 207Pb and 204Pb compared to the baseline of 208Pb and 206Pb.The largest NVEdriven MIFs are 0.043‰()and-0.040‰()among all the studied species relative to Pb0 vapor at 500 °C.The magnitudes of odd-mass isotope MIF()and even-mass isotope MIF()are almost the same but with opposite signs,leading to the MIF ratio of them(i.e.,)is-1.08.
Keywords Mercury and lead isotopes·Crystals·Nuclear volume effect·DFT relativistic effect calculations
1 Introduction
The nuclear volume effect(NVE)term,also known as the nuclear field shift effect(NFSE),was first proposed in spectroscopy studies(Stacey 1966;Heilig and Steudel 1978;King 1984;Aufmuth et al.1987).It is a mass-independent isotope fractionation driven by differences in volumes and shapes of nuclei for heavy elements(Schauble 2013).Fujii et al.(1989a,b)first reported an anomalous isotope effect ofU in U(IV)and U(VI)isotope exchange reactions.There are also anomalous isotope effects ofGd andZn in liquid-liquid extraction experiments(Chen et al.1992;Nishizawa et al.1993),which was known as the‘‘odd-even isotope effect’’(Nishizawa et al.1994).Nishizawa et al.(1995)attributed an anomalousSr isotope effect founded in liquid-liquid extraction of strontium chloride using a crown ether to isotope shift in atomic spectra(field shift).Nomura et al.(1996)also found an anomalous isotope effect ofU in the U(IV)-U(VI)exchange reaction,which was caused by the nuclear volume effect.
Bigeleisen modified the conventional Bigeleisen-Mayer equation(Bigeleisen and Mayer 1947;Urey 1947)and added the NVE item into the new equilibrium isotope fractionation calculation formula for heavy elements(Bigeleisen 1996).He also concluded that the NVE has a weak influence on chemical bonds and it was only secondorder correction(Bigeleisen 1998).Therefore,the NVE has only a minor effect on the vibration frequency,i.e.,it has only a minor effect on the conventional mass-dependent fractionation based on vibrational frequencies.However,Bigeleisen(1998)indicated that the NVE could independently cause significant isotope fractionations for heavy elements already via the changing of ground-state electronic energies of isotopologues.Subsequently,significant isotope fractionations of heavy elements have been reported due to the NVE,such as U(Bigeleisen 1996;Nomura et al.1996;Abe et al.2008a,b,2010),Hg(Schauble 2007;Wiederhold et al.2010;Ghosh et al.2013;Yang and Liu 2015),Tl(Schauble 2007;Fujii et al.2013;Yang and Liu 2015;Fang and Liu 2019)and Pb(Yang and Liu 2015).
NVE-driven equilibrium isotope fractionations for many heavy metal systems have been studied experimentally,including Ti,Zn,Zr,Fe,Gd,Nd,Cr,Sr,Mo,Ru,Te,Cd,Hg,Tl,and Pb,etc.(Fujii et al.1998a,b,1999a,b,2000,2002,2006a,b,2008,2009a,b,c,2010,2011a,b;Nishizawa et al.1998;Shibahara et al.2002a,b;Bergquist and Blum 2007;Estrade et al.2009;Ghosh et al.2008,2013;Moynier et al.2009a,b;Wiederhold et al.2010;Zheng and Hintelmann 2009,2010).Moynier et al.(2013)summarized the results of NVE-driven U and Tl isotope composition changes in natural environments.Yang and Liu 2016 reviewed the nuclear field shift effects on stable isotope fractionation mainly about theoretical treatment details.
With the increasing experimental studies on NVEs,people began to theoretically investigate the NVE-driven fractionations of heavy elements in small gas-and aqueous-phase isotope systems,including Hg(Schauble 2007;Ghosh et al.2008;Wiederhold et al.2010;Yang and Liu 2015),Tl(Schauble 2007;Fujii et al.2013;Yang and Liu 2015),U(Abe et al.2008a,b,2010),Zn(Fujii et al.2010),Ni(Fujii et al.2011b)and Pb(Yang and Liu 2015).The theoretical calculations of U,Hg,Tl,and Pb obtain the same conclusion,which NVE-driven isotope fractionations are larger than the conventional mass-dependent fractionations for heavy metal isotope systems.However,the calculated NVE-driven isotope fractionations of Zn and Ni are smaller than the conventional mass-dependent ones.
For large systems,e.g.,crystalline materials,it will be no longer suitable for using the tiny electronic energy difference caused by the isotope substitution,compared to the extremely large total electronic energies,to calculate the final isotope fractionation.The electron density method was hence proposed as an alternative way to calculate the NVE(King 1984;Bigeleisen 1996;Fujii et al.2009a).Schauble(2013)calculated the nuclear volume effects of Cd,Sn,and Hg in crystals by using the projector augmented wave method(DFT-PAW)with a three-dimensional periodic boundary condition based on the density functional theory(DFT).Nemoto et al.(2015)established a two-component relativistic method(IODKH-IOSO-MFSO)for computing NVE of heavy elements,which was with almost equivalent accuracy but 30 times faster than the previous four-component method by DIRAC software package and could compute lager isotope systems for future NVE investigation.Fang and Liu(2019)calculated the NVE-driven isotope fractionations of several Tl-bearing compounds and Tl-bearing aqueous solutions.They also investigated the Tl isotope fractionations caused by adsorption on mineral surfaces.Méheut et al.(2020)theoretically investigated the main potential driving processes in magmatic Zr-bearing minerals and bulk rocks,which the results showed NVE-driven fractionation is up to 0.08‰on δ/Zr at 800 °C.
Because under high temperature,where those crystalline compounds formed,the conventional mass-dependent fractionations are negligible.Here we calculate the NVEdriven fractionation factors of mercury and lead in crystals by calculating electron densities at the nuclei using the density functional theory(DFT).Many isotope fractionation factors of crystalline compounds are provided for the first time.Our calculations evaluate quantum relativistic effects of Hg and Pb atom with all-electron ZORA approach.
2 Methods
2.1 Nuclear volume effect(NVE)
The NVE is proportional to the difference in ground-state electronic energies.For the isotope exchange reaction(AY+AX=AX+AY),the NVE(i.e.,lnK)is written as(e.g.,Bigeleisen 1996):

where Eis the ground-state electronic energy and AX and AX represent compounds with different isotopes;k is Planck and Boltzmann constants;T is the absolute temperature.
The nuclear volume effect is also found in proportion to the electron density at the nucleus(King 1984;Bigeleisen 1996;Fujii et al.2009a;Schauble 2013).The electron density at the nucleus is expressed as|Ψ(0)|:

where δT is the difference of NVE-driven energies for two isotopes;C is the scaling factor,i.e.,C=Ze/6ε(Almoukhalalati et al.2016)(Zis the atomic number of element A;e is an elementary charge(1.60217733910C); εis the permittivity of free space(8.854187817910F/m));|Ψ(0)|is the electron density at the nucleus of the atom;δ<r>is the difference in mean-square nuclear charge radii of two isotopic nuclei and the mean-square nuclear charge radii of Hg and Pb isotopes are from Angeli and Marinova(2013)(Table 1).Therefore,the NVE of species A relative to species B(δE=δT-δT)is

where δEis the difference of NVE-driven energies for two species;lnαis the isotope fractionation caused by NVE.
2.2 Mass-independent fractionation(MIF)
The same methods were used in previous calculations(e.g.,Yang and Liu 2015)for mass-independent fractionations(MIFs)of Hg and Pb isotopes.Here,we take Hg isotopes as an example to describe the concept of mass-independent isotope fractionation(MIF).
The MIF of any pair of Hg isotopes(e.g.,Hg/Hg)will be


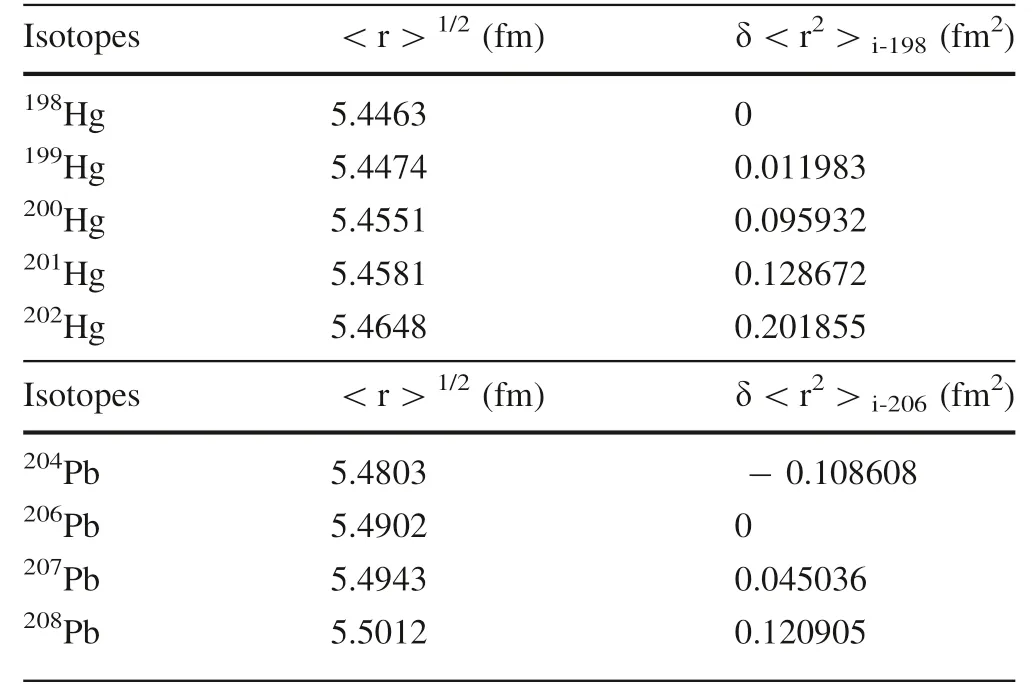
Table 1 Values of root mean square charge radius(<r2>1/2)of Hg and Pb isotopes

where λis calculated using the high-temperature approximation of equilibrium fractionation(Young et al.2002):

Meanwhile,λis calculated from the mean square nuclear charge radii(Schauble 2007):

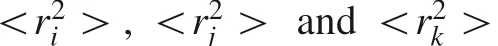
The relative MIF in comparison of Hg vapor(Hg)is hence calculated by

The values of λand λfor Hg and Pb isotope systems are shown in Table 2.
2.3 Computational details
Un-optimized crystal structures are used for electron densities at nuclei calculations in BAND module with relativistic spin orbit ZORA method in combination with the generalized gradient approximation(GGA-PBE)density functional of amsterdam density functional(ADF)software package(Velde and Baerends 1991;Wiesenekker and Baerends 1991;Franchini et al.2013,2014;Philipsen et al.2019).Because the unit cell and structural optimizations of crystal structures have a minor effect on calculated electron densities at nuclei(Schauble 2013).QZ4P basis sets are used for Hg and Pb.TZ2P basis sets are used for Br,Te,and Cr.TZP basis sets are used for other small atoms(e.g.,C,O,S).BAND module is available for the study of threedimensional periodic boundary condition systems.All studied crystal structures are shown in Figs.1 and 2,which is from the materials project(Jain et al.2013)and American Mineralogist Crystal Structure Database(Downs et al.2003).

Table 2 Conventional massdependent(CMD)and nuclear volume(NV)scaling factors of Hg and Pb isotope systems
3 Results
3.1 NVE-driven fractionations of mercury in crystals
NVE-driven equilibrium fractionation factors of mercury in crystals relative to Hgvapor(i.e.,Hg)in terms ofHg/Hg are presented in Fig.3 and Table 3 calculated by AMS software package.Fractionation factors are reported in terms of 1000·lnα
NVE-driven equilibriumHg/Hg fractionations range from 0.12‰ to 0.49‰,at 1000°C(Fig.3 and Table 3).All calculated crystals(oxidized phases)enrich heavier isotope(Hg)relative to Hgvapor,where Hg,Hgand Hgare with the electron configuration as[Xe]6s4f5d,[Xe]6s4f5dand[Xe]4f5d,respectively.It is consistent with the rule of thumb heavy isotopes tend to enrich in oxidized phases rather than reduced phases in redox reactions.Because NVEs can cause isotopes with larger nuclear charge radii to prefer to enrich in the fractionation species with smaller s electrons or more p,d,and f electrons,where the electrons in s-orbital cause larger electron densities at nuclei than p-,d-,f-orbitals.

Fig.1 Crystal structures of mercury modeled in this study from the materials project(Jain et al.2013)and American Mineralogist Crystal Structure Database(Downs et al.2003)

Fig.2 Crystal structures of lead modeled in this study from the materials project(Jain et al.2013)and American Mineralogist Crystal Structure Database(Downs et al.2003)

Fig.3 NVE-driven equilibrium fractionation factors(1000·lnαNV)of mercury in crystals relative to Hg0 vapor in terms of 202Hg/198Hg
3.2 NVE-driven fractionations of lead in crystals
NVE-driven equilibrium fractionation factors of lead in crystals relative to Pbvapor(i.e.,Pb)in terms ofPb/Pb andPb/Pb are shown in Fig.4 and Tables 4 and 5 calculated by AMS software package.
NVE-driven isotope fractionations are up to-0.20‰(Pb/Pb),-0.08‰(Pb/Pb)of Pb-bearing crystal species,0.17‰(Pb/Pb)and 0.06‰(Pb/Pb)of Pb-bearing crystal species relative to Pbvapor,at 1000 °C(Fig.4 and Tables 4 and 5).Pb-bearing crystal species enrich heavier isotopes(Pb andPb)than Pb-bearing crystal species,which the enrichment can be up to 0.37‰(Pb/Pb)and 0.14‰(Pb/Pb)at 1000 °C,due to their NVEs are in opposite directions.
3.3 MIFs of mercury and lead in crystals
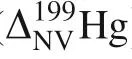

Table 3 CalculatedΔ|Ψ(0)|2,δEfs and NVE-driven equilibrium fractionation factors(1000·lnαNV)of mercury in crystals relative to Hg0 vapor in terms of 202Hg/198Hg

Fig.4 NVE-driven equilibrium fractionation factors(1000·lnαNV)of lead in crystals relative to Pb0 vapor in terms of 208Pb/206Pb and 207Pb/206Pb

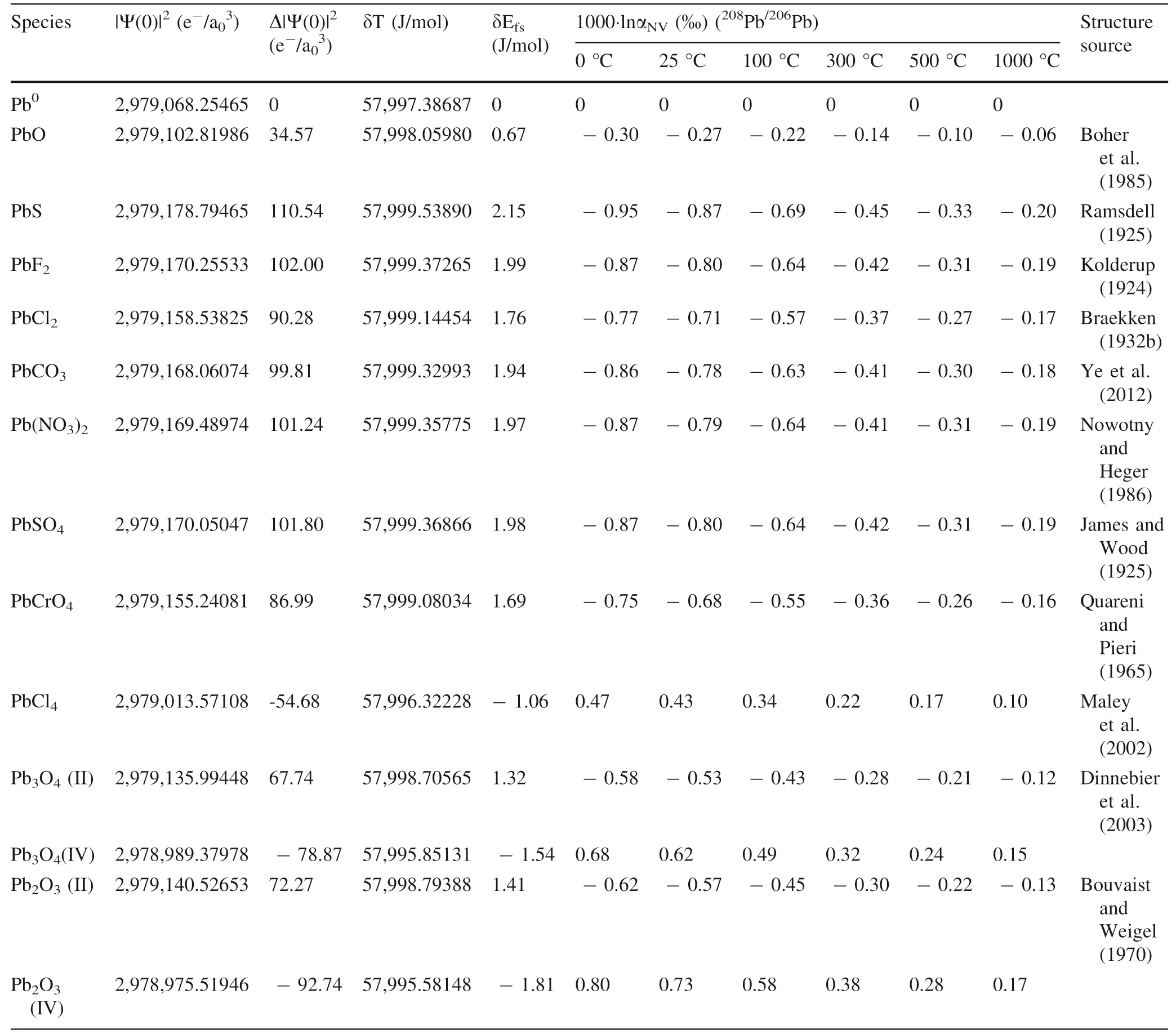
Table 4 CalculatedΔ|Ψ(0)|2,δEfs and NVE-driven equilibrium fractionation factors(1000·lnαNV)of lead in crystals relative to Pb0 vapor in terms of 208Pb/206Pb
4 Discussion
NVE-driven equilibrium fractionations of Hg-bearing crystal species(e.g.,HgCl)are smaller than Hg-bearing crystal species(e.g.,HgCl,HgO).The main exceptions are HgTe and HgBr,which their 1000·lnαare smaller than that of HgFand the NVE-driven fractionation of HgBris even smaller than that of HgCl.NVEdriven fractionations of HgXand HgXdecrease with the increasing mass number of halogen(i.e.,HgF>HgCl>HgBr,HgF>HgCl>HgBr),which X represents F,Cl and Br.Because the differences in electron densities at the nucleus of HgFand HgFrelative to Hgvapor are respectively larger than that of HgCl,HgBr,HgCland HgBr,leading to a larger NVE-driven equilibrium isotope fractionation of HgFand HgF.
For all studied Hg-bearing crystal species,the largest isotope fractionation is found in HgFrelative to Hgvapor,which is also much larger than that of HgCland HgBr.Large fractionation of HgFrefers to the differentelectronegativity of F,Cl,and Br and coordination numbers compared to the other two species(i.e.,HgCland HgBr).The electronegativity of F is larger than that of Cl and Br,and the coordination number(CN)of HgFis much larger than HgCland HgBr[i.e.,CN(HgF)->CN(HgCl)=CN(HgBr)](Fig.1),causing a much larger difference in electron density at the nucleus of Hg atom in HgFcrystal relative to Hgvapor.
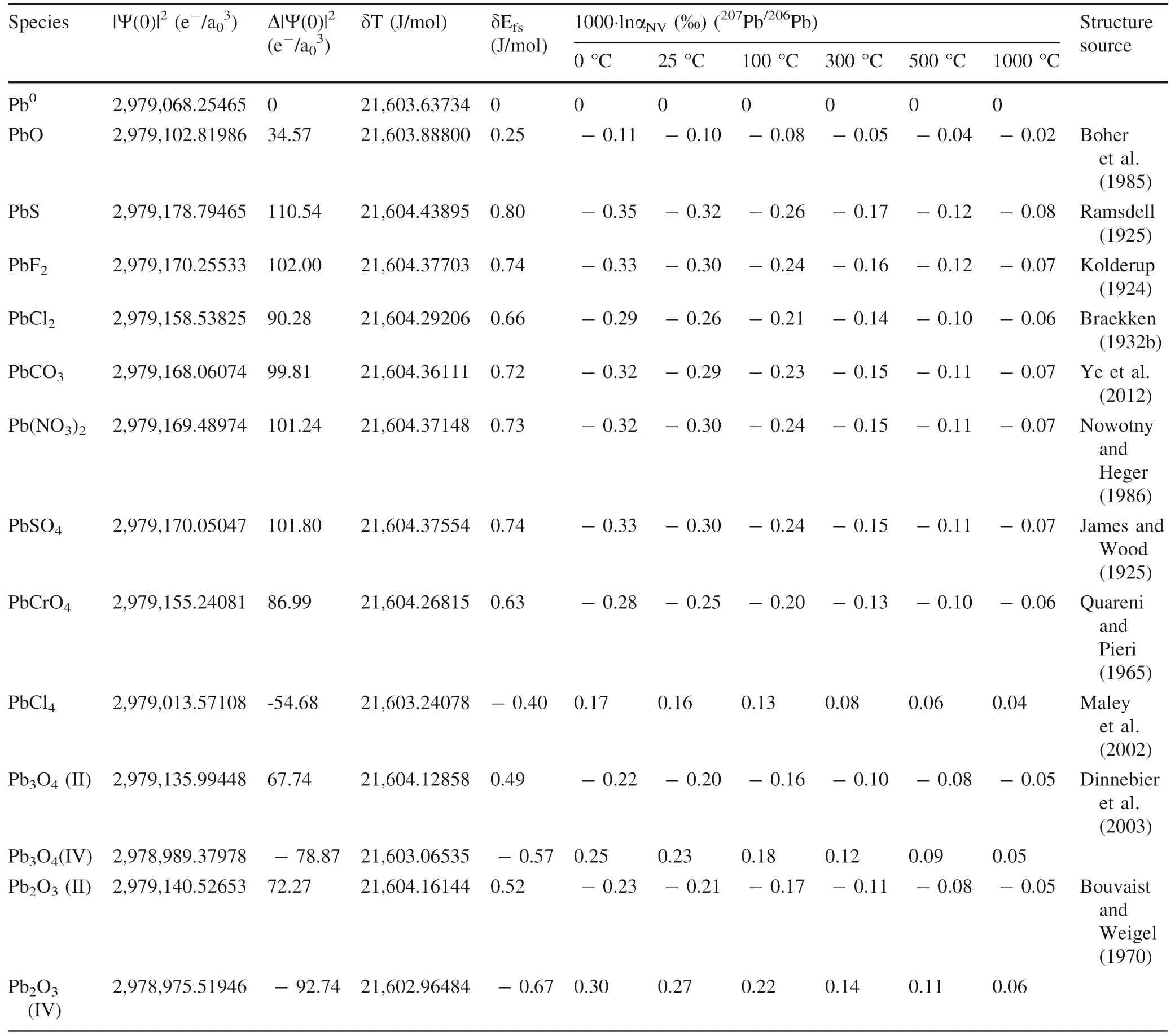
Table 5 CalculatedΔ|Ψ(0)|2,δEfs and NVE-driven equilibrium fractionation factors(1000·lnαNV)of lead in crystals relative to Pb0 vapor in terms of 207Pb/206Pb
The electronegativity of O is larger than that of S and HgO and HgS have the same coordination number.Similar to the mercury halide system,the fractionation of HgO should be theoretically larger than that of HgS caused by the nuclear volume effect.The NVE-driven fractionation of HgO is smaller than that of HgS due to the difference in electron density at the nucleus of Hg atom in HgO is smaller than that in HgS relative to Hgvapor in our calculations.We suspect this abnormal phenomenon is mainly due to the different structures of these two crystals although they have the same coordination numbers(Fig.1).The crystal system of HgO is orthorhombic,however,the crystal system of HgS is hexagonal.
Comparing with the previous study(Table 3),our NVEdriven Hg isotope fractionation results are noticeably different from those of Schauble(2013).The difference between Schauble(2013)and our results are due to the different calculated methods,software packages,crystal structures,the nuclear charge radii,and values of the scaling factor(i.e.,C)were used.The calculations ofSchauble(2013)were made with the ABINIT software package using the Perdew-Wang functional in the local density approximation(PW)and the Perdew,Burke,and Ernzerhof functional in the generalized gradient approximation(PBE).Our calculations are made with the BAND module in Amsterdam Modeling Suite(AMS)software package using the relativistic spin orbit ZORA method in combination with the Generalized Gradient Approximation(GGA-PBE)density functional.Schauble(2013)used the nuclear charge radii of Fricke and Heilig(2004)(i.e.,<r>ofHg andHg are 5.462 fm and 5.443 fm)and the nuclear charge radius difference(δ<r>=<r>-<r>)is 0.207fm.But we use the nuclear charge radii from Angeli and Marinova(2013)(i.e.,<r>ofHg andHg are 5.4648 fm and 5.4463 fm)and the nuclear charge radius difference(δ<r>=<r>-<r>)is 0.2019fm.The value of the scaling factor(i.e.,C)of Schauble(2013)is 0.166 in a·fm·J/mol which is larger than that of this study(C=0.157 in a·fm·J/mol).If the same nuclear chargeradii and the difference in electron density at the nucleus(i.e.,Δ|Ψ(0)|)were used,a larger scaling factor will induce larger equilibrium isotope fractionations.

Table 6 NVE-driven mass-independent fractionation values for different Hg bearing species in crystals relative to Hg0 vapor
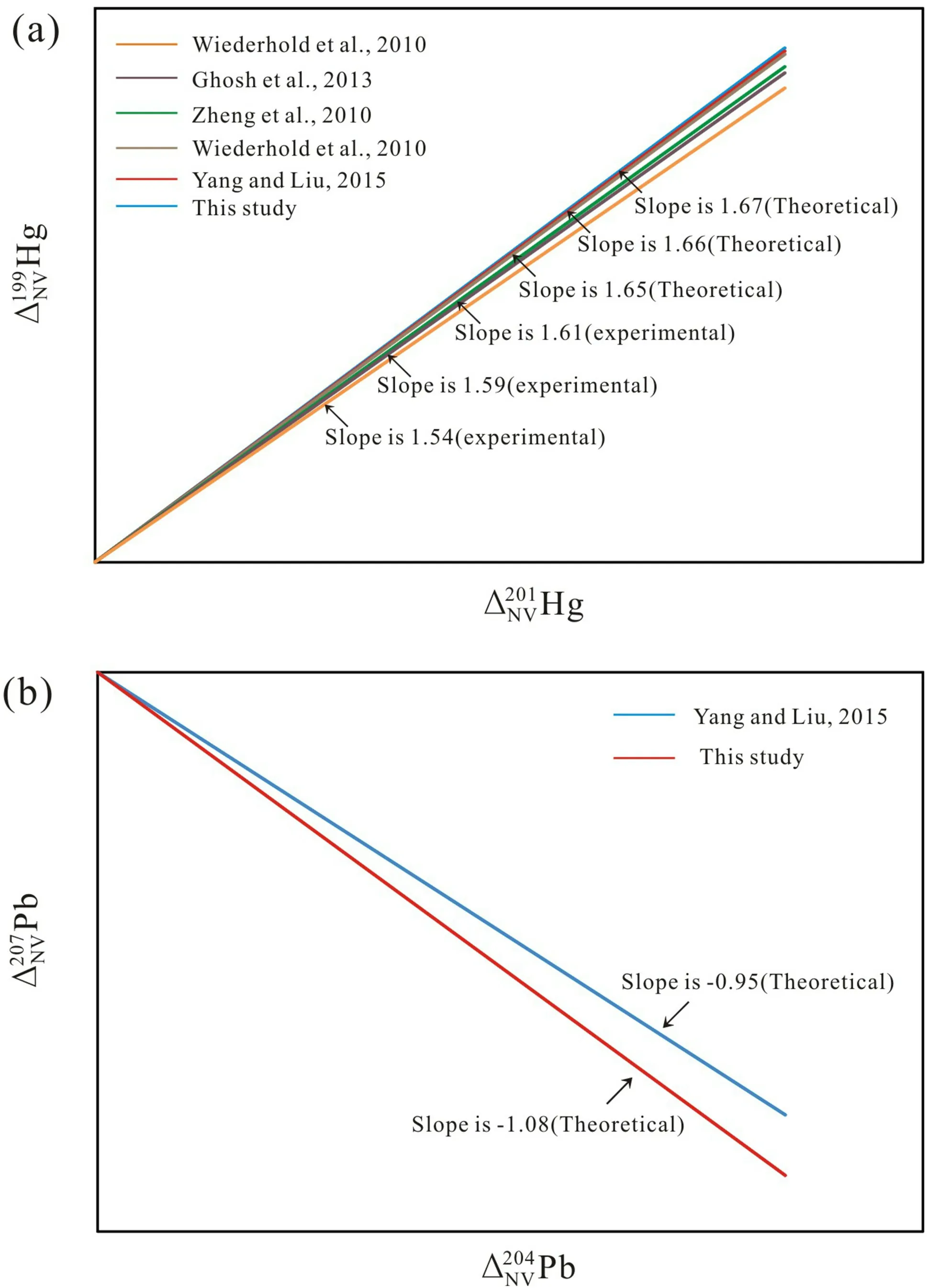
Fig.5 a Slopes ofΔNV199Hg/ΔNV201Hg from NVE comparing with previous experimental and theoretical studies.b Slopes ofΔNV207Pb/ΔNV204Pb from NVE comparing with the previous theoretical study

Table 7 NVE-driven mass-independent fractionation values for different Pb-bearing species in crystals relative to Pb0 vapor
NVE-driven fractionations of Pb-bearing crystal species(e.g.,PbS)are larger than that of Pb-bearing crystal species(PbCl)except for PbO,PbCl,PbO,PbOThis result is different from the previous research(Yang and Liu 2015),in which the NVE-driven fractionations of Pb-bearing gaseous species are much larger than those of Pb-bearing gaseous species.We contribute this phenomenon to the differences in electronegativity and coordination number.For instance,the fractionation of PbClis much larger than that of PbCldue to their different coordination number(CN(PbCl)>CN(PbCl)),although the signs of NVEs are opposite to each other.
Similar to the mercury halide system,NVE-driven fractionations of PbXdecrease with the increasing mass number of halogen(i.e.,PbF>PbCl)which X represents F and Cl.This result is consistent with the rule of thumb.The NVE can cause large isotope fractionations for salt compounds of Pb in crystals[i.e.,PbCO,Pb(NO)and PbSO]and their magnitudes are almost the same due to the smaller differences in electron densities at nuclei of Pb in these three crystals.This result suggests these three different acid radical ions have almost the same effect on NVE-driven fractionations.
Similar to HgO and HgS,the fractionation of PbO are smaller than PbS caused by the nuclear volume effect due to the difference in electron density at the nucleus of Pb in PbO crystal is smaller than that in PbS relative to Pbvapor.It is mainly attributed to the different coordination numbers of these two crystals[i.e.,CN(PbS)>CN(PbO)](Fig.2).Both PbOand PbOinclude two valence states,i.e.,Pb(II)and Pb(IV),where the magnitudes of NVEdriven fractionations for Pb(II)-bearing crystals are smaller than those of Pb(IV)-bearing crystals due to the larger coordination numbers of Pb(IV)-bearing crystals than that of Pb(II)-bearing crystals although the signs of their NVEs are in opposite direction.
Comparing with precious calculated results of smaller gaseous and aqueous mercury and lead systems(Yang and Liu 2015),the NVE-driven equilibrium isotope fractionations in crystals are almost smaller.For example,the NVEdriven equilibrium isotope fractionations of gaseous HgCland HgBrare 1.45‰ and 1.40‰,where the NVE-driven equilibrium isotope fractionations of crystalline materials(HgCland HgBr)are 0.90‰ and 0.54‰ at 25 °C.Therefore,the magnitudes of NVE-driven fractionations depend on the values of the scaling factor(i.e.C),the choice of the nuclear charge radii,crystal structures,and calculated methods.
5 Conclusion
In this study,we have theoretically calculated isotope fractionations of mercury and lead at equilibrium between several crystals and their vapors caused by the nuclear volume effect.NVE-driven fractionations of Hg and Pb are range from 0.12‰ to 0.49‰(Hg/Hg),from-0.06‰ to-0.20‰(Pb/Pb),from-0.02‰ to-0.08‰(Pb/Pb)for Pb-bearing species,from 0.10% to 0.17‰(Pb/Pb)and from 0.04‰ to 0.06‰(Pb/Pb)for Pb-bearing species in crystals relative to Hgvapor and Pbvapor at 1000 °C,respectively.All calculated Hg-bearing species in crystals enrich heavier isotope(Hg)relative to Hgvapor.Pb-bearing species enrich heavier Pb isotopes(Pb andPb)than Pb-bearing species in crystals,which the enrichment can be up to 0.37‰(Pb/Pb)and 0.14‰(Pb/Pb)at 1000 °C,due to their NVEs are in opposite directions.
Acknowledgements
This research was supported by National Natural Science Foundation of China(NSFC)projects(41703012)and Qinghai Science and Technology projects(2018-ZJ-956Q).Y.L is grateful for the supports of the Strategic Priority Research Program(B)of CAS(XDB18010100,XDB41000000),and pre-research Project on Civil Aerospace Technologies No.D020202 funded by the Chinese National Space Administration and NSFC projects(41530210).- Acta Geochimica的其它文章
- Effect of crustal porosity on lunar magma ocean solidification
- Gold anomaly ranking based on stream sediment geochemistry in the Fariman-Kashmar axis,NE Iran
- Petrographic and geochemical characterization of weathered materials developed on BIF from the Mamelles iron ore deposit in the Nyong unit,South-West Cameroon
- Estimation of evaporation losses based on stable isotopes of stream water in a mountain watershed
- Geochemical significance of tricyclic and tetracyclic terpanes in source rock extracts from the Offshore Niger Delta Basin,Nigeria
- Paleoclimate evolution and aridification mechanism of the eastern Tethys during the Callovian-Oxfordian:evidence from geochemical records of the Qiangtang Basin,Tibetan Plateau

