Effect of crustal porosity on lunar magma ocean solidification
Mingming Zhang·Yingkui Xu·Xiongyao Li
Abstract The lunar ferroan anorthosites,formed by plagioclase flotation from the crystallization of the lunar magma ocean,have an age span of over~200 Ma.However,previous thermal models predicted a much shorter time range.We propose that a much smaller thermal conductivity of anorthositic crust due to its high porosity may have delayed the solidification of the lunar magma ocean.Our thermal simulation results,using the thermal conductivity of porous lunar crust,show that crystallization of a 1000 km deep magma ocean could be prolonged to tens of millions of years,and up to 180 Ma under some extreme conditions.The porous crust alone can’t explain the large crustal age span,however.Other circumstances must be taken into consideration,such as a thick lunar soil.
Keywords Porosity·Thermal evolution·Ferroan anorthosites
1 Introduction
The Moon is believed to be a product of a giant impact between proto-Earth and a Mars-sized impactor(Hartmann and Davis 1975;Cameron and Ward 1976).Consequently,at least a majority of the infant Moon could be melted,which is known as the lunar magma ocean(thereafter,LMO)hypothesis(Smith et al.1970;Wood et al.1970),due to highly energetic collision and rapid accretion(Canup and Asphaug 2001).Samples from Apollo missions provide solid evidence that lunar anorthositic crust is a primary product of LMO differentiation(Taylor 2016),and its solidification extends from 4.47 to 4.29 billion years before the present(Borg et al.2015;Fig.1).Lunar magma ocean crystallization process can be divided into two stages(Snyder et al.1992;Elardo et al.2011;Elkins-Tanton et al.2011;Sakai et al.2014;Lin et al.2017).
The first stage mainly crystallizes olivine and pyroxene at the bottom of residual magma ocean since adiabat changes much smaller than liquidus with depth and would intersect with liquidus at some depth where crystallization occurs(Elkins-Tanton 2012).During this epoch,the surface of magma ocean would remain as free liquid(Herbert et al.1977b;Elkins-Tanton et al.2011),because any chilled magma due to exposure to cold stellar space is denser than liquid magma underneath,vigorous convection and meteoritic impacts would disintegrate quenched material and bring it downwards into hot magma(Walker et al.1980;Spera 1992),although some research would argue the presence of a stable anorthositic crust formed at its very beginning(Xu et al.2016).The high-temperature liquid surface would radiate energy at a rate of>10W m,orders of magnitude higher than thermal conduction.Accordingly,the first~80 vol% of magma ocean would cool in just 10-10years(Elkins-Tanton et al.2011).When plagioclase becomes a liquid phase,it will crystallize at the bottom and float to the surface,forming an anorthositic crust.The most significant aspect of this crust,in terms of thermal evolution,is that it blocks heat loss efficiently and delays the solidification of the last~20 vol% residual magmas.However,the last dreg of magma would possibly crystallize in 10 Ma according to a comprehensive LMO evolution model of Elkins-Tanton et al.(2011),much shorter than geochronology analysis from ferroan anorthosites(FANs)samples.Solomon and Longhi(1977)and Meyer et al.(2010)also modeled the age of FANs by assuming a priori plagioclase lid,an invalid premise that violates the results of petrological experiments.Therefore,the discrepancy between dated FANs ages and modeled ones has not been fully reconciled yet.

Fig.1 Chronology of lunar anorthosite rocks,compared with solar system formation and Moon formation(Borg et al.1999,2011;Marks et al.2014;Carlson and Lugmair 1988;Norman et al.2003;Nyquist et al.2006,2010;Alibert et al.1994;Bouvier and Wadhwa 2010;Yin et al.2002)
Essentially,the thermal evolution of LMO is regulated by an initial heat budget and rate of heat loss.The initial heat budget is always associated with its giant impact origin and is not well constrained.The two-stage evolution model of the magma ocean,on the one hand,divides crystallization into two regimes,i.e.,equilibrium and fractional crystallization;on the other hand,it sets up two corresponding thermal evolution schemes.Heat loss during the first stage is very efficient when magma ocean has a free liquid surface and can be characterized by Stefan-Boltzmann law(Elkins-Tanton et al.2011).This stage is considered transient.The rate-limiting stage is the second one because heat loss mode is transformed from blackbody radiation to conduction.From Fourier’s law of heat conduction,heat flux is a product of thermal conductivity and temperature gradient.Thus,thermal conductivity is a key ingredient of thermal evolution.More often than not,lunar and other planetary bodies’thermal evolution models use constant thermal conductivity in the range of 2-4 W mK(e.g.Solomon and Longhi 1977;Wieczorek and Phillips 2000;Elkins-Tanton et al.2011).This range is mainly derived from minerals and rocks on Earth at room temperature(e.g.Murase and McBirney 1970;Cermak and Rybach 1982;Clauser and Huenges 1995;Schumacher and Breuer 2006).The conditions under which thermal conductivity was measured may not be applicable to the Moon.The lunar anorthositic crust is heavily cratered and its fractures,cracks,and porosities are well preserved.Researches on porous chondrites and planetesimals show that thermal conductivity can be drastically reduced by porosity as much as three orders of magnitude(Yomogida and Matsui 1984;Hevey and Sanders 2006;Henke et al.2012).Due to small thermal conductivity,highly porous anorthosites would serve as a blanket covering the remaining magma ocean and insulate internal heat from being lost.Thus,in this study,we propose that porous anorthosites have a vital influence on LMO thermal evolution and may keep some of the lunar interiors as liquid till 4.29 Ga ago.
In this study,we will first briefly introduce the procedure of solving energy conservation equations numerically that control LMO solidification process.Then the following section will describe the impact of porosity of anorthosites on their thermal conductivity,followed by three models that increase in complexity.Finally,we will also discuss the possible factors that may affect LMO thermal evolution.
2 LMO solidification
The depth of LMO is poorly constrained.McLeod(2016)thoroughly discussed the possible scale of LMO,ranging from 400 to 1000 km,based on aluminum mass balance and geophysics.We will use 1000 km in all three models for a good comparison with that of Elkins-Tanton et al.(2011).
The crystallization of LMO follows Elkins-Tanton et al.(2011)and Snyder et al.(1992).Detailed descriptions can be found in these two studies.To simplify the problem,we divide LMO evolution into two stages.According to Elkins-Tanton et al.(2011),the first stage crystallizes olivine and pyroxene at the bottom of LMO,leaving a liquid surface.This stage extends to 80% of the initial magma volume.The second stage,however,grows plagioclase besides olivine,pyroxene,and oxides.The volume ratio β between plagioclase and other minerals during this stage does not hold constant,in other words,β=0.5 when 80-87 vol%magma ocean is solidified;otherwise,β=0.4.

During the second stage,plagioclase and other minerals will co-crystallize at the base of the remaining magma ocean.Plagioclase is lighter than surrounding liquids and floats to the surface immediately after its formation,whereas other minerals(olivine,pyroxene,and oxides)stay still at the bottom due to their higher densities.The temperature of the crust surface is set as constant 250 K(Langseth et al.1976;Hevey and Sanders 2006),whilst the temperature at bottom of the magma ocean is set as solidus.The solidus of residual magma is defined as the temperature at the base of residual magma ocean where crystallization occurs and is a function of pressure and chemical composition.Following Meyer et al.(2010),solidus is calculated as:

where Tis solidus temperature in K,r is the radius in km,and Vis residual liquid fraction relative to initial volume.Furthermore,the temperature profile within the residual liquid follows an adiabat.
In the following,we divide the volume of 20% of the initial magma ocean into 1000 equal sub-volumes,each step crystallizes one part.During each step,the residual liquid fraction can be considered as constant,as an approximation.Then,we solve the heat balance equation numerically at the base of the crust(r=r):

where k is the thermal conductivity of crust,H,C,ρ and L are heat production rate of radioactive decay,specific heat capacity,density,and latent heat of residual magma,respectively.These parameters are listed in Table 1.Note that the present abundances of radioactive energy sourcesU,U,Th,andK should be extrapolated backward to the time of lunar formation.The present abundance of Thorium,Uranium,and Potassium concentrations are adopted from(Anders and Grevesse 1989;Hagee et al.1990).Heat production rates(watts per kilogram of isotope)and decay constants can be found in Turcotte and Schubert(2014)and Haenel et al.(1988).By multiplying density,concentration,volume,and heat production rate,and then summing up these four isotopes,we have the energy contribution of radiogenic heating H.
The left side of Eq.(2)is the energy conducted through the crust;on the other side,these three parts represent energy sources in residual liquid,i.e.,radioactive energy,sensible heat,and latent heat.It is the heat flux at the bottom of the crust that controls the solidification lifespan of the magma ocean,as easily seen from Eq.(2).During this step,the internal heat is continuously transferred to stellar space by solving Fourier’s law of heat conduction and calculation stops when the temperature of the next step at the base of the crust is reached.Then,the next onethousandth volume is added to the bottom of the crust and the top of the solidified mantle.The same procedure is undertaken until the LMO is completely solidified.Unlike Maurice et al.(2020),we consider solidified magma as static cumulates for simplicity.
3 Effect of crustal thermal conductivity on LMO solidification
3.1 Thermal conductivity of anorthosites
Thermal conductivity of certain material is a function of composition,porosity,temperature,ambient pressure,and fluids content(Cermak and Rybach 1982;Clauser and Huenges 1995;Vosteen and Schellschmidt 2003;Schön 2015).FANs on the Moon are rather anorthositic.Amongsamples listed in Warren(1993)and Wieczorek(2006),only a few of them contain mafic minerals more than 10 wt%.As Wieczorek(2006)pointed out,the massweighted average plagioclase in FANs is 93 wt%.In addition,accessory minerals are mostly absent in FANs(Wieczorek 2006).Thereby,FANs are modeled as 93 wt%plagioclase plus 7 wt% pyroxenes.Moreover,different anorthite content can result in a large difference in thermal conductivity(Horai and Simmons 1971),this requires that the plagioclase,for its overwhelmingly high anorthite content,should be treated as pure anorthite.The monomineralic anorthite aggregates have a thermal conductivity of 1.68 W mKat room temperature(Horai and Simmons 1971;Schön 2015);while pyroxene(mostly high-Ca pyroxene)is 4.66 W mK(Clauser and Huenges 1995;Schön 2015),and mass-weighted average thermal conductivity of anorthosites is 1.89 W mK.It follows Sass(1965)that aggregates of crystals typically have lower conductivity values than monomineralic anorthosite,arising from contact effects of intergrains(Binder and Lange 1980;Schön 2015).We thus infer that anorthosites may be more thermally resistant.
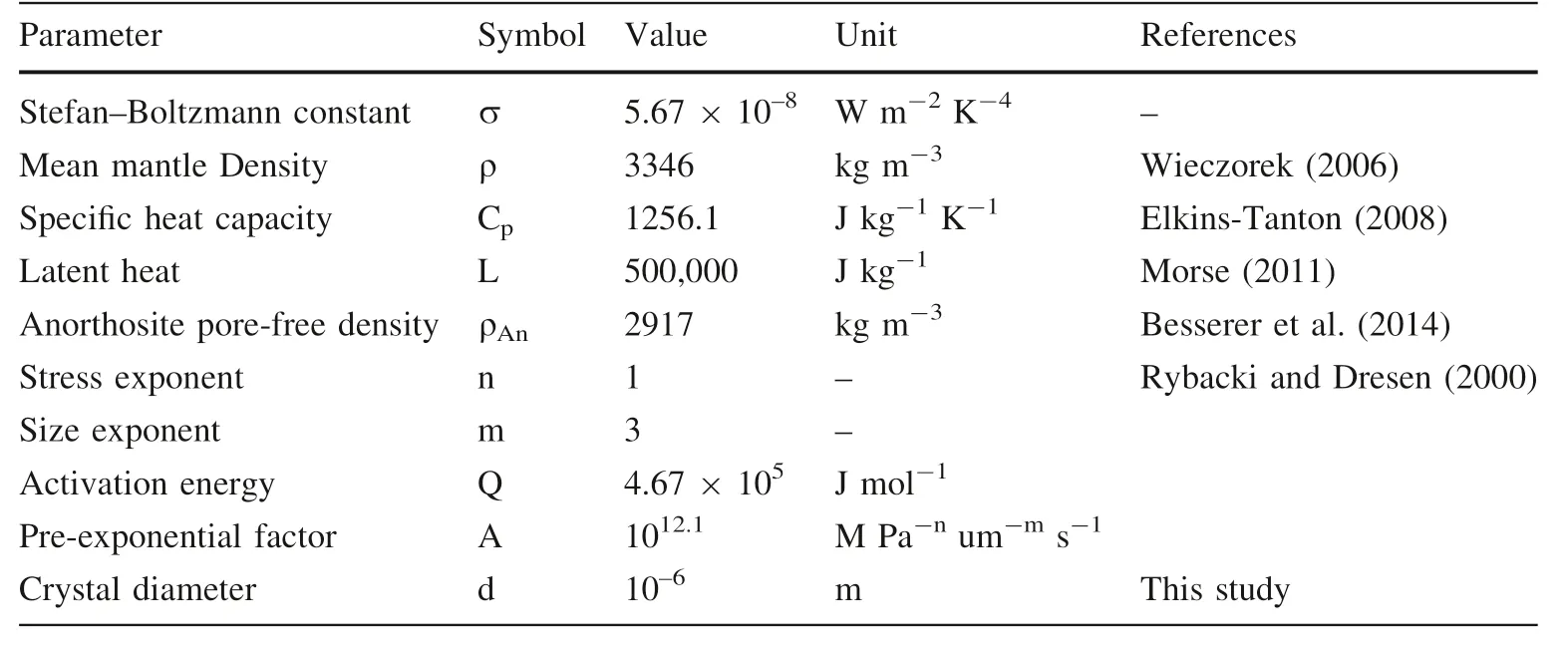
Table 1 Parameters used in this study
3.1.1 Dependence on T,P
The temperature influence of thermal conductivity has been confirmed by many experiments,(Murase and McBirney 1970;Clauser and Huenges 1995;Vosteen and Schellschmidt 2003).In particular,the conductivity of synthetic pore-free lunar basalts(10,022)in a large temperature range,for example from room temperature up to 1500 °C(e.g.Murase and McBirney 1970),exhibits asymptotically decrease till melting point,where the conductivity reaches its minimum,one-sixth of room temperature value.However,plutonic rocks rich in feldspar including anorthosites do not show such a strong correlation,instead,conductivity decreases slightly with temperature(Clauser and Huenges 1995).We hence assume that FANs possess conductivity just independent of temperature.This assumption is valid in our model since the temperature range of lunar anorthite crystallization is~1400 K calculated by the MELTS program(Smith and Asimow 2005)using the BSM composition of(Elkins-Tanton et al.2011),comparable with the temperature range of Clauser and Huenges(1995).
The dependence of conductivity for pore-free materials on ambient pressure is not well constrained compared with temperature.Ross et al.(1984)showed that,though not for rock-forming minerals,the thermal conductivity of crystalline material increases with ambient pressure on the GPa scale.For rock-forming minerals,Yukutake and Shimada(1978)and Seipold and Gutzeit(1980)conducted very precise measurements and showed that pore-free minerals,in terms of thermal conductivity,are insensitive to pressure at least 10 kbar.In the case of the Moon,the lunar crust of average thickness 34-43 km(Wieczorek et al.2013a)has pressure up to 0.2 GPa,small enough that pressure effect on pore-free lower crust can be ignored.From the discussion above,we conclude that neither temperature nor pressure in our model would contribute remarkably to thermal conductivity.
3.1.2 Dependence on porosity
Besides,the effect of fluids content in rock voids,if any,should be ignored,inferred from results of Clauser and Huenges(1995).The lunar anorthosite could have~1 wt% volatiles at most,according to Hui et al.(2013).Here,we find porosity(φ)to be the utmost factor that influences the thermal conductivity of FANs.Porosity may originate from dislocation of grains due to differential thermal expansion(Clauser and Huenges 1995),meteorites impact,and inherent voids(like holes in vesicular basalts).

Fig.2 Relationship between porosities and ages of anorthosites.Porosity from(Kiefer et al.2012b);age from(Gaffney et al.2008;Daubar et al.2002;Grange et al.2016;Nyquist et al.1991,1977,2005,2007,2009;Dalrymple and Ryder 1996;Shih et al.1985;Meyer et al.1996;Borg et al.2011;Stettler et al.1973;Murthy et al.1971;Kirsten and Horn 1974)
Recently,the mean porosity values of dozens of lunar samples have been upgraded,including Apollo samples and lunar meteorites(Kiefer et al.2012a,b).These are regarded as on-the-Moon bulk porosities because alteration of meteorites by terrestrial weathering is a negligible factor(see supplementary materials in Wieczorek et al.2013a).Figure 2 summarizes the ages and porosities of their samples.Ages are collected from Meteoritical Bulletin Database(https://www.lpi.usra.edu/meteor/)and Lunar Samples(https://www.lpi.usra.edu/lunar/samples/),Lunar and Planetary Institute.They are considered as genesis time based on resistance to shock events of geochronometers,in the order Sm-Nd,Rb-Sr,U-Pb,according to Borg et al.(2015).77,035 and NWA4932 haven’t been dated yet;NWA482 has only Ar-Ar age.So it may represent a little higher porosity accumulation rate.It seems that the porosities do not correlate with ages or rock types,broadly consistent with statistical results(Consolmagno et al.2008).The fact that the porosities do not cumulate with ages implies that the porosities could be an indigenous feature of these rocks,or the current porosities represent a steady-state between the effect of impact cracking and porosity generating rate.Both feasibilities indicate that lunar rocks during or soon after their formation should have the same porosities as they currently do.The maximum porosity is a little bit higher than 20%.Confining pressure induced fracture decrease would be the most likely factor in reducing porosity within a few kilometers below the surface.This is because loose materials like lunar soils become closer packed by grains rolling and gliding under low pressure(Henke et al.2012).Güttler et al.(2009)determined porosities variation with pressure range 10-100 bar,equivalent to 2 km below the lunar surface,and porosities decrease to 0.42 from 0.88,representative values of lunar soils.In the following,we will employ three models,each using a different depth-dependent porosity distribution,to evaluate the influence of thermal conductivity on LMO thermal evolution.
3.2 Thermal conductivity profiles within anorthosites
When plagioclase starts to form at magma’s bottom,it will float to the magma surface forming a nascent lunar crust.This crust could not be a single homogeneous crystal,but possibly a local shell of plagioclase aggregates,because plagioclase cannot crystallize everywhere simultaneously and reach the surface at the same time.Different aggregates or rockbergs will eventually join together,giving birth to a complete global shell of crust(Herbert et al.1977a).
This process will inevitably result in imperfect contact between crystals and aggregates.Whatever the cause of porosity,meteoritic impact,inherent bubbles,or differential thermal cracking,we argue that there are indeed some pores in the primitive crust.Thermal conductivities of rocks and soils that have porosities up to 60% have been summarized by Warren(2011)and Keihm and Langseth(1977).An exponential fitting equation is acquired by Warren(2011):

where kis non-porous conductivity,here taken as 1.89 W mK.Thus,rocks with φ=0.2 have conductivities~0.156 W mK.Interestingly,Henke et al.(2012)independently derived a similar analytical expression from H and L chondrites data:

where φ=0.08.This formula yields an almost identical result.We infer that the porosity reducing effect on the conductivity is likely to be independent of materials and thus Eqs.(3)and(4)can be more reliably applied to the Moon.Figure 3 illustrates the relationship between thermal conductivity and porosity defined by Eq.(3).The upper limit of porosity is 0.6 corresponding to the lunar surface,where thermal conductivity is approximately three orders of magnitude smaller than pore-free anorthosites.

Fig.3 Relationship between thermal conductivity and porosity
In the following,three models of porosity distribution will be demonstrated.We firstly consider a simple case,model A,in which a homogeneous porosity is at all depth.This uniform porosity is taken as 20% in light of measurements(Kiefer et al.2012a,b).This model is oversimplified and is included here because it serves as a basis to discuss the relationship between porosity and thermal evolution.In this model,any parcel of forming crust is assumed to have 20% porosity,and specific heat capacity and density are constants.
Thermal evolution is shown in Fig.4.Figure 4a depicts the temperature profile for four selected times,0 Ma,30 Ma,100 Ma,190 Ma;Fig.4b displays the growth of the solidifying mantle and crust.Therefore,this simplified model,for an initial composition of,shows that the last drop of magma will freeze at~190 Ma after lunar formation.Apparently,both mantle and crust crystallize at a higher rate during earlier times.
In model B,a more realistic porosity profile is considered.High-resolution lunar structure from GRAIL indicates that density or porosity changes with depth below the surface(Wieczorek et al.2013b).Additionally,seismic data proves that there is a steady increase of density within uppermost~20 km,under which a rather stable layer exits down to lunar Moho(Toksöz et al.1974;Khan et al.2013).Since Apollo 12 and 14 landing sites are in a region that has a similar vertical density feature to the far side(Besserer et al.2014),we tentatively assume that this discontinuity exists 20 km below the lunar surface globally as a primary feature,regardless of later mare basalts eruption.As a consequence,the uppermost~20 km crust has an increased thermal conductivity,while the conductivity deeper than 20 km is invariable.
Han et al.(2014)set up a model with a suite of reasonable scenarios.The porosity follows an exponential decrease:


Fig.4 a Temperature profiles of four selected time,0 Ma,30 Ma,100 Ma,190 Ma.The temperature in residual liquids is adiabatic,shown as a nearly vertical temperature profile.b Mantle and crust growth with time.Mantle and crust met at~1691 km when the last drop magma solidified,~190 Ma after lunar formation.
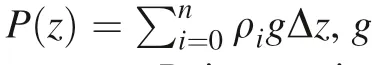
Again,Binder and Lange(1980)suggest another exponential decrease of porosity:

where φis surface porosity set as 0.2.Factor 6.5 is an e-folding depth in km.With the help of Eqs.(3)or(4),the conductivity profiles are obtained.Once a shell of crust is formed,according to its depth,it is assumed to have a porosity corresponding to that of the same depth.This assumption,though unrealistic to some extent,is good to match the final porosity profile.In model C,we will try to make up for this defect.
We also try a similar distribution but with e-folding depth and surface porosity being 10 km and 0.24,respectively(Besserer et al.2013),i.e.,φ(z)=0.24e.A linear porosity distribution is also possible(Besserer et al.2014),φ(z)=0.24-0.012z.
On the other hand,Wieczorek et al.(2013a)suggest that porosity may extend to lunar uppermost mantle.Accordingly,an exponential decrease in porosity throughout the entire crust is modeled under the same pattern.A comparison between these porosity profiles is made in Fig.5.These results can be classified into two categories.The first category has a surface porosity of 0.2,giving rise to shorter crystallization time.While the second one has a longer evolution time due to higher porous.Unexpectedly,the little porosity difference between the two categories leads to a clear discrepancy in total evolution time.Perhaps most importantly,all these models fail to account for anorthosites’large age coverage,though porosity does have a noticeable influence on thermal evolution.

Fig.5 a Five porosity profiles within the lunar crust.The discontinuity around 20 km is an artificial truncation assumed by the corresponding model because porosity near 20 km is about a few percent,not exactly zero.b Corresponding results of five porosity profiles.Solid curves are the growth of crust,meanwhile dotted curves are the solid front of the crystallizing mantle.
In model B,the presumption of the latest formed crust having some certain porosity is possibly not in accordance with reality.The temperature of anorthosites right after its crystallization,generally above 1000 K,is high enough that the thermal annealing effect could take place above the solidification front.Thus,some inherent pores in anorthosites could be squeezed out.In model C,in the following,both overburden pressure and thermal annealing are taken into account,giving a real-time adaptive porosity profile synchronous with the ongoing solidification of LMO.Rocks,when subjected to long-term stress,tend to deform permanently,and if the temperature is close to their melting point,they will be much easier to adjust shapes.Minerals and rocks will finally adapt themselves to mutual geometric shapes and fill voids in between.This process is termed thermal annealing or sintering.The creep rate of olivine crystal powders has been experimentally determined by Schwenn and Goetze(1978)in 1000-1600 °C range.Henke et al.(2012)and Yomogida and Matsui(1984)utilize it to model the sintering process of porous planetesimals.In terms of anorthosites,the parameters of Rybacki and Dresen(2000)are made use of.From volume conservation,we have:

where A is the pre-exponential factor,ε is stress in MPa,here taken as hydrostatic pressure,n is stress exponent,d is particle size in um,m is size exponent,Q is the activation energy in J mol,R is the universal gas constant 8.314 J molK,and T is the temperature in K.This equation relates the time rate of porosity reduction and strain rate,very similar to the one used by Schwenn and Goetze(1978),Yomogida and Matsui(1984)and Henke et al.(2012).The activation energy is,though highly dependent on water content(Rybacki and Dresen 2000),insensitive to stress,grain size,or porosity(Schwenn and Goetze 1978).Thus,despite the high porosity of Schwenn and Goetze(1978)or the low porosity of Rybacki and Dresen(2000),we take Q as a constant.In the lunar crustal pressure range,the dominant deformation is supposed to be diffusion creep,according to Rybacki and Dresen(2000).Parameters are listed in Table 1,Q is 4.67×10J molif the Moon is dry.The strain rate employed by Yomogida and Matsui(1984)is physically identical to that of Rybacki and Dresen(2000).The particle diameter is taken as a critical value that convective magma would allow anorthite crystals to be not trapped in(Solomatov 2007):

Parameters are surface heat flux F,thermal expansivity α,density contrast between anorthite and magmaΔρ,and magma viscosity η.For reasonable values,e.g.,Δρ=450 kg m, α=5×10K, η=10 Pa s(Dygert et al.2017),the critical diameter is a few microns.
In order to constrain the depth of porous crust,we define an annealing depth,d,the depth where the last 0.1%porosity diminishes within 100 years.This tells us that crust with porosities smaller than 0.1% will be annealed within 100 years,short enough that can be considered as an instant compared with geological time scale.A brief estimation gives the strain rate should be higher than 3.2×10s.Therefore,the corresponding annealing depth can be numerically determined according to Eq.(7).The porosity distribution above annealing depth is then following an exponential with surface porosity 20%;while porosity below annealing depth is set as 0.Figure 6 is the annealing depth evolution and residual magma ocean crystallization.Admittedly,it would take a shorter time to a full crystallization because porosities between annealing depth and crust surface during cooling are smaller than final values.
3.2.1 Surface powdered matter insulation
As manifested by model B,a higher porosity of surface materials will dramatically delay magma solidification.Therefore,we infer that the uppermost highly porous layer of the lunar crust might have a strong insulation effect.A 20 m layer of loose matter with porosity up to 60% at the surface could possibly postpone the cooling of magma ocean to a great extent,as represented by Fig.7.With the first layer of 10 m having 60%pores,a second 10 m being 36%(Warren 2011),and 20 m below surface following porosity distribution of Wieczorek et al.(2013a),the residual magma ocean extends to 180 Ma,almost 4 times longer than the one without surface highly porous material in model B.Thus,a 20 m thick highly porous layer could possibly explain FANs large age span.
4 Discussion
4.1 Comparison with the previous model

Fig.6 Time evolution of annealing depth and growth of mantle and crust

Fig.7 Porosity profile and LMO solidification.Black dashed line stands for porosity,with the uppermost layer the most porous,60%.Below,the porosity profile of Wieczorek et al.(2013a)is adopted
Our model is a ramification of Elkins-Tanton et al.(2011).The solidus equation we adopted is based on the thickness of the lunar crust of 47 km,thicker than Wieczorek et al.(2013a).A thinner anorthosite crust changes the initial BSM,which further alters the solidus curve.However,due to the large volume of LMO,the effect of a few kilometers anorthosites on solidus could be modest.On the other hand,this setup benefits us a better comparison between our results and Elkins-Tanton et al.(2011).Their model yielded 7 Ma to complete solidification.However,even in the adaptive porosity case,it would take magma ocean 25 Ma to solidify,several times longer.Therefore,porosity in the lunar crust should be considered in thermal evolution.
It’s interesting to note that we have noticeable different results from Maurice et al.(2020)wherein they achieved~178 Ma magma ocean lifespan with a similar thermal conductivity of porous-free anorthositic crust in a pure conduction scheme.This discrepancy comes from magma’s internal heat source.They adopted U,Th,K abundances from Taylor(1982),~4 times higher than those in CI chondrites(Anders and Grevesse 1989;Hagee et al.1990).Additionally,we don’t include partitioning of these elements between residual magma and solid,instead,they are uniformly distributed in solidified cumulates and residual magma.We admit that their model is more reasonable with respect to radioactive decay,and can be incorporated in future models.
4.2 Highly porous surface layer
Most people will argue the rationale of a highly porous layer on the lunar surface.Those porosities were taken from present lunar soil.The most uncertain factor perhaps is its thickness.The thickness of this layer has an accumulative tendency with its age(Nakamura et al.1975),and the mean rate after Imbrian Period is~0.2 mm Ma(Craddock and Howard 2000).This extremely low rate would contribute to lunar soil less than one meter since the Imbrian Period.This implies that the majority of present lunar soil originated from late heavy bombardment and before.If present lunar soil stemmed from late heavy bombardment only,then we suspect there should be more soil because impacts would be more frequent during crust formation.If this is the case,our presumption will be valid.The reason why we don’t see a thicker soil is that soil made during crust formation may undergo a sintering process due to relatively high temperature under the lunar surface.On the other hand,if present lunar soil was produced from both late heavy bombardment and before,we infer there would be some soil,for example,half of its present thickness,on the surface of the Moon during crust formation.Overall,some soil atop crust during crust formation is reasonable.And the truth is the surface powdered matter is extremely efficient in keeping the magma ocean warm.
4.3 Lunar surface temperature
Among these parameters in thermal models lies one important factor,lunar surface temperature.This is treated very roughly over the decades.Most literature takes as 250 K,for reasons like Apollo mission in situ heat flow measurements(Langseth et al.1976),or astronomical constraints on nebular temperatures(Woolum and Cassen 1999).However,we find this arbitrary set of temperatures to be oversimplified,and the lunar surface would be very hot after its formation.Recent studies on the atmosphere of rocky exoplanets demonstrate that rocky planets could be smothered by hot dense silicate vapor or atmosphere(Zahnle et al.2007;Lupu et al.2014).Thus,after the catastrophic formation of the Moon,it would be surrounded by a hot cloudy silicate vapor.This is partially proved by the detection of SiO from Spitzer space telescope(Lisse et al.2009)and theoretical modelling(Saxena et al.2017).Based on LMO crystallization model of Elkins-Tanton et al.(2011),Saxena et al.(2017)concluded a 10Pa,3000 K(sub-Earth point)atmosphere just 1 year after formation and 300 Pa,2300 K(sub-Earth point)some 400 years after formation.We,therefore,believe that the infant Moon right after its formation would possess some atmosphere,and this atmosphere would keep the lunar surface warm/hot for some time.Once plagioclase formed and floated up to the surface,under the blanketing effect of the atmosphere,it would stay as hot as its solidus or so,rather than 250 K.
Certainly,as the atmosphere dissipates gradually,the surface temperature will drop to~250 K.But neither the question of how long the atmosphere would last nor how surface temperature changes with time is clear.To simply demonstrate how lunar surface temperature would dramatically change thermal evolution of LMO,we assume a linear surface temperature drop with time,i.e.,T(t)=T-(T-250)t/t,where Tis the melting point of plagioclase here taken as 1390 K,tis the time scale for surface temperature drop from Tto 250 K.It’s very hard to determine t,thus we use a series of t,1000 years,10,000 years,10 Ma,50 Ma and 200 Ma.
5 Conclusion
We conducted a series of thermal evolution models of lunar magma ocean with different porosity distributions in lunar crust included.Model results suggest that porosity of lunar crust could lead a very different magma ocean solidification process than previous studies which generally neglected crustal porosity.Finally,our results have the following conclusions:
1.Thermal conductivities of anorthosites are smaller than those generally used ones,especially when some pores present;
2.A smaller thermal conductivity will delay the solidification of LMO a few tens of million years.However,this cannot reconcile the discrepancy between the age span and classical crystallization model;
3.Surface loose matter,if exists at the very beginning of crystallization of the LMO,could possibly keep LMO warm till 180 Ma after Moon formation,but its thickness should be~20 m.
Acknowledgements
We thank Dr.Kiefer S.Walter for the discussion on the porosities of lunar samples.Dr.Linda Elkins-Tanton provided many useful suggestions and details of thermal modeling.Dr.Phonsie J.Hevey and Dr.Ian S.Sanders offered us insight into sintering process.This work was financially supported by the National Natural Science Foundation of China(Grants Nos.41773064,41931077),the Strategic Priority Program of the Chinese Academy of Sciences(No.XDB41020300),Youth Innovation Promotion Association of CAS,the Key Research Program of the Chinese Academy of Sciences(XDPB11),Beijing Municipal Science and Technology Commission(Z181100002918003).- Acta Geochimica的其它文章
- Geochronology,geochemistry and Hf isotopes of andesites in the Sandaowanzi gold deposit(Great Xing’an Range,NE China):implications for petrogenesis,tectonic setting,and mineralization
- Geochemical characterization of the salinity of irrigated soils in arid regions(Biskra,SE Algeria)
- Adsorption experiment of water-soluble rare earth elements in atmospheric depositions and implications for source tracing in South China
- Effects of geosorbent and solution properties on sorption and desorption of PAHs
- Paleoclimate evolution and aridification mechanism of the eastern Tethys during the Callovian-Oxfordian:evidence from geochemical records of the Qiangtang Basin,Tibetan Plateau
- Geochemical significance of tricyclic and tetracyclic terpanes in source rock extracts from the Offshore Niger Delta Basin,Nigeria

