基于小波矩的智能手绘草图识别系统设计
郑新涛,苏道玉
(河北地质大学,河北 石家庄 050031)
0 引言
手绘草图作为一种人体内在思想的外化表达方式,可通过抽象和隐喻的方式实现思想情绪的传递和交流,相较于传统的图形工具,具备形象、直观、简洁、清晰地描述模糊概念等特点,有助于人们开展创造性强的活动[1⁃3]。传统的智能手绘草图识别模式是按照传统分类,在抽象的智能手绘草图内容识别中存在许多问题,发展至今这些问题依旧没有得到解决。因为操作者在绘图中的水平能力不一,以至于同一类别草图的外形具有高度抽象性,且草图没有颜色和纹理[4]。但是它却拥有自然图像不具备的笔画顺序信息,这种笔画顺序信息的存在可以有效提升智能手绘草图的识别效果。
小波矩是一种新型不变矩,由具备平移、旋转、缩放不变形的不变矩和小波变换共同组成,能够清晰地展现不同尺度下图像的整体信息和局部细节信息,在图像处理方面应用较为广泛[5⁃6]。为此,本文设计一种基于小波矩的智能手绘草图识别系统。该系统充分利用小波矩可同时提供时域、频域,更好地采集智能手绘草图的特征优势,实现智能手绘草图的有效、精准识别。
1 基于小波矩的智能手绘草图识别系统
1.1 系统结构
图1 描述了在MVC(Model View Controller)模式下划分的基于小波矩的智能草图识别系统的框架结构图,此系统应用Javax.swing 等类库和Java 程序语言设计。

图1 系统结构图
草图控制模块可为编写多种图形操作提供了有力支撑,是MVC 模式中的控制,可实现草图界面模块和草图数据模块的有效控制[7]。草图界面模块和草图数据模块执行接收到来自草图控制模块的操作指令,对绘图处理流程进行调控,对笔划种类进行有效辨识,同时完成草图存储的有效控制。草图控制模块通过预处理子模块对手绘草图进行预处理后,通过草图识别子模块进行草图图形识别和草图内容识别,并利用操作控制子模块和手势命令识别子模块完成草图的控制和绘图笔划识别。操作者可以利用各种输入设备在手势书写界面中绘制草图并勾画笔划作为操作指令,利用手势命令识别子模块进行操作指令识别。草图数据模块的作用是存储系统中的各项数据,其中包括两种数据文件,分别为草图数据文件和XML 数据文件。草图数据文件保存草图信息,XML 数据文件保存已经定义好的手势命令规范数据。
系统的草图界面模块是系统的操作界面,结构非常简单,通过按钮触发动态训练调整指令,其他所有命令都需利用笔划控制。系统功能有笔式交互方式、笔划类型的识别和处理、训练并获取用户习惯以及笔划作为命令执行对应操作。
1.2 预处理子模块
系统草图控制模块中的预处理子模块实现手绘草图的预处理。受输入条件限制及输入习惯不同影响,手绘草图中包含噪声,所以需要对草图进行预处理。同时预处理还可以得到分割笔划的结果,为手绘草图图形的有效识别奠定基础[8⁃10]。为了去除笔划冗余点和曲线闭合误差等噪声,需要对笔划进行预处理:清除冗余点和聚点、修正端点以及对闭包进行计算。笔划分割器则是以笔划预处理为前提,选择笔划特征判断最佳分点并以最佳分点为基准完成笔划的分割。以上的笔划预处理与笔划分割器两部分构成了整个预处理子模块的预处理过程。
1.3 草图图形识别
由基本图元识别器与组合图元识别器两部分共同实现草图图形识别,草图图形识别是系统的核心技术。草图图形识别流程如图2 所示。用户通过草图界面模块的手势书写界面输入手绘草图的绘制结果后,通过第1.2 节分析的预处理子模块中的笔划预处理以及笔划分割器得到手绘草图的预处理结果后;使用基本图元识别器通过形状拟合笔划,得到笔划的直线段基本图元、弧段基本图元以及椭圆基本图元;再通过组合图元识别器组合这些基本图元获取组合图元,将其存储在模板库,实现草图图形识别。

图2 手绘草图图形识别过程
2 基于小波矩的手绘草图内容识别
草图控制子模块中采用基于小波矩的手绘草图识别方法完成草图内容识别。识别草图内容时,草图本身会发生一些改变,导致采集的草图特征发生改变,该现象不会影响人体视觉对草图的识别[11]。小波矩能够较好的抗噪并拥有目标旋转不变性的特点,为了使手绘草图图像在操作中发生平移旋转和缩放等改变时草图图像本身特征不变[12],系统选择小波矩实现对草图内容的有效识别。
2.1 不变矩基本理论
用二维亮度分布f(x,y)表示1 幅草图,函数值f(x,y)表示点(x,y)处草图像素的亮度值。
设f(x,y)为草图的亮度函数,定义其(a+b)阶矩函数如下:

式中:υ为x⁃y平面上草图的区域,用于表示f(x,y)函数的定义域区间;rab(x,y)(矩的权核)表示与υ内(x,y)相关的连续函数;a,b是整数。
2.2 小波不变矩
小波变换可实现草图图像局部特征的有效提取,因为利用其提取图像特征过程中可在提供时域窗口的同时提供频域窗口[13]。设ja(m)为基函数,子波函数表示为:

式中p和q分别为伸缩因子和平移因子。
通过替换基函数ja(m)为小波基函数rp,q(m)获取小波不变矩。将3 次B 样条小波函数作为母小波r(m),将其描述为:

式中:B样条的阶次i为3;尺度因子p、调制系数f0和离差量分别为0.706 569,0.397 917 和0.605 412。
在小波基函数中选取3 次样条小波进行特征提取,因为它拥有有限次平滑性、对称性以及高斯逼近性等特点,在时域和频域上的局部信息优势较大,形式与Zernike 多项式矩相似,可以让相似形状形体的识别和图像局部特征的提取更稳定、更有效[14]。
子波函数的离散化过程为:

式中参数p,q一般选择离散值。
控制图像的大小在m≤1 范围内,设参数p0,q0为0.5,则p,q分别是:
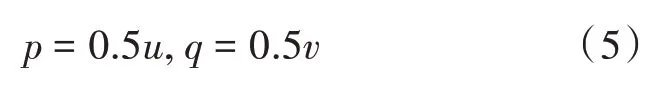
式中:u=0,1,2,…;v=0,1,2,…,uv+1。
则小波函数基为:

草图全局信息、局部信息的提取,可通过选取不同的u值、v值实现。为了对草图目标进行分类,需要加入一组小波不变矩,通过式(7)描述:

式中,将基函数ja(m)替换为ru,v(m),u=0,1,2,…,v=0,1,2,…,2u+1,b=0,1,2,…。通过式(7)描述发现Hu,v,b为Zb(m)的小波变换,在某一固定m值处,Zb(m)=描述草图f(m,ϑ)在相位域0 ≤ϑ≤2π的范围内第b个频域特征。取不同的尺度因子p、平移因子q,保证小波函数ru,v(m)遍及整个径向空间,从而小波不变矩就可以反映图像f(m,ϑ)在不同尺度上的特征。
2.3 手绘草图内容识别流程
图3 描述了基于小波矩的手绘草图内容识别流程:创建目标草图库;归一化预处理草图库中的草图;归一化草图后采集其小波矩特征,将其保存到与草图库连接的特征数据库[15];利用适宜小波基函数计算草图的小波矩特征值;计算样本草图和草图库中草图小波矩特征值的欧氏距离D(x,y)=,设2 幅草图对应的特征向量为x,y,设特征分量为xi,yi。通过样本草图欧氏距离的顺序大小排列草图库中的草图,识别目标草图内容。
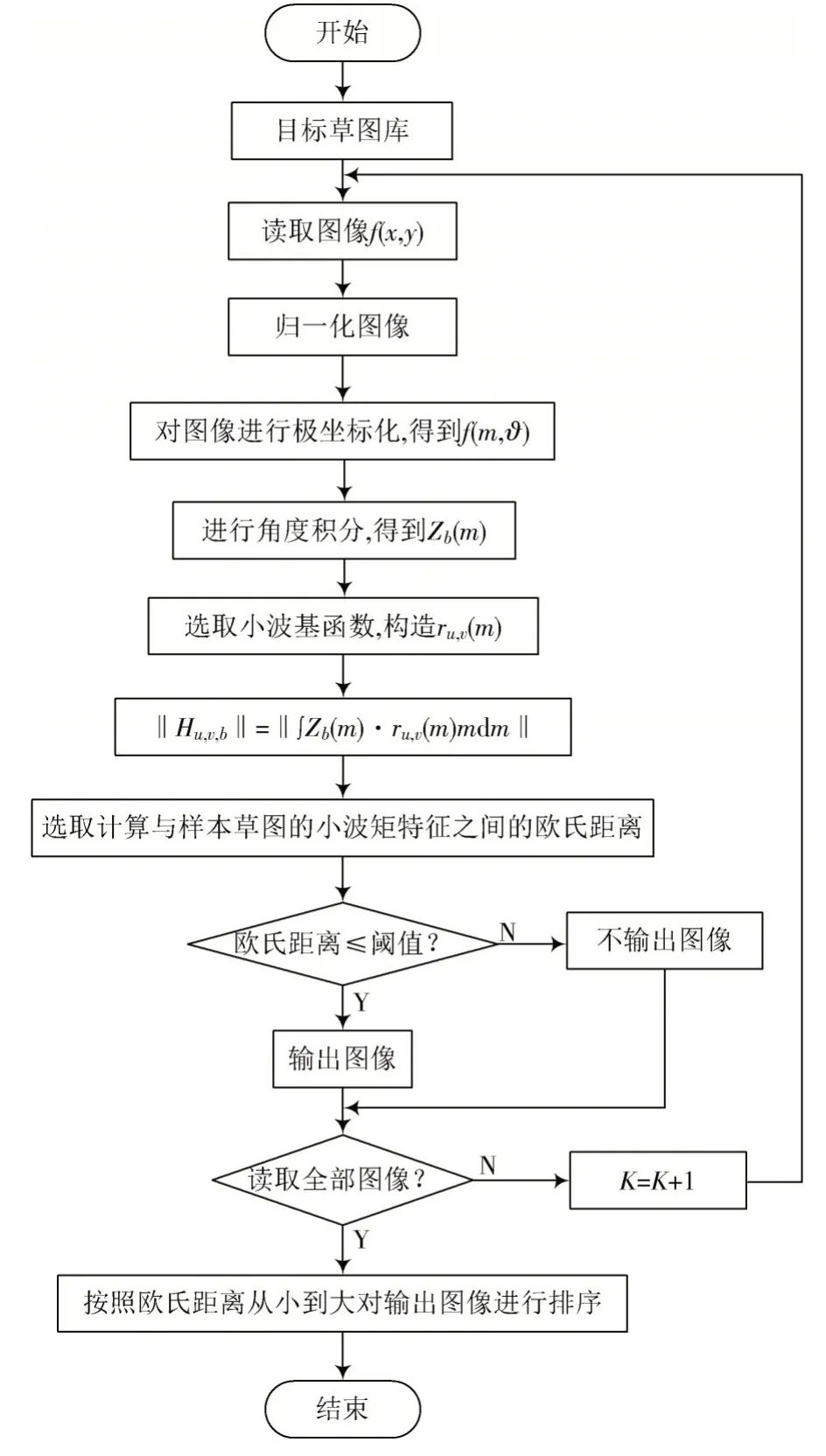
图3 手绘草图内容识别流程
3 实验分析
本文选取Microsoft Windows XP 的实验平台,利用小波工具箱进行实验分析,对基于小波矩的智能手绘草图系统的有效性和优越性进行检验。
3.1 手绘草图识别效果
实验选取一张手绘草图,如图4a)所示,利用本文系统对该手绘草图中的图像内容进行识别。通过本文系统预处理子模块去除草图的曲线闭合误差以及笔划冗余点聚点等噪声,完成笔划的分割及形状拟合笔划。利用草图识别子模块的图元识别器识别笔划,最终得到清晰草图,如图4b)所示。说明本文系统可有效去掉原图像的噪声,使得手绘草图更加清晰完整,为图像的有效识别提供良好基础。

图4 手绘草图
3.2 小波矩不变性实验分析
为了检验本文系统在草图发生变化时小波矩能够保证其特征不发生变换,选取一张手绘企鹅草图如图5a)进行实验。实验分别对样本草图进行90°旋转、180°旋转、2 倍放大、2 倍放大并旋转90°的操 作,如图5b)~图5e)所示。本文系统采用小波矩对小波不变矩数值进行采集,并对发生比例和位置尺度变换的草图进行归一化处理。

图5 实验草图样本
实验样本草图特征值(小波不变矩数值)对比结果如表1 所示。

表1 经过旋转比例变换下的小波不变矩数值
分析表1 数据可得到,图5a)~图5c)的小波不变矩数值验证了本文系统小波不变矩的旋转不变性。图5d)、图5e)验证了本文系统小波不变矩尺度变换和旋转尺度变换的不变性。草图在发生旋转、比例变换、位置尺度变换时,本文系统的小波不变矩较为稳定,每组草图之间的差距较小,验证了小波不变矩拥有位置尺度变换、比例变换和旋转不变性的特点,本文系统能够满足智能手绘草图的精准、稳定识别。利用本文系统对发生过比例、位置尺度变换和旋转的草图样本进行识别,识别结果见图6。其中,图6 左侧为识别前图像,图6右侧为识别后图像。分析图6 发现,识别后的图像与样本草图图5a)一致,证明了本文系统在手绘草图识别过程中,可有效确保识别内容的有效和稳定。

图6 识别图像
4 结论
本文利用小波矩的位置尺度变换和旋转不变性设计基于小波矩的智能手绘草图识别系统,实现智能手绘草图图形和内容的稳定、有效识别。并以企鹅的草图样本为例,对其进行旋转、放大,采集其小波不变矩数值,检验本文系统可有效利用小波矩在草图发生位置尺度变换、比例变换和旋转时具备的不变性实现手绘草图识别。实验结果表明,本文系统的应用能够有效提升对草图内容的识别稳定性和有效性,对智能手绘草图内容的识别提供强有力的支持。

