概率布尔控制网络的集可控

苟志丽,徐 勇,王金环

(河北工业大学理学院,天津 300401)

1 引言

布尔网络(Boolean networks,BNs)是Kauffman于1969年提出的用于复杂非线性生物系统建模的一类逻辑动态系统[1].BNs由一组离散时间变量组成,每个变量只能取0或1,其表示一个基因的活性.基因间高度结构化的相互作用可以通过布尔函数来描述,布尔函数通过特定的逻辑规则确定每个基因的状态.BNs已经被证实是描述、模拟和分析基因调控网络、社会系统和神经网络的重要工具[2–5].

最近,Cheng等人首先提出两个任意维数矩阵相乘的运算,即矩阵的半张量积(semi-tensor product of matrices,STP)[6].STP的显著优点是可以将BNs转换成一个代数系统,从而更好地研究BNs的相关问题.带有外部输入的BNs称为布尔控制网络(Boolean control networks,BCNs).文献[6–7]为研究BCNs中许多经典控制理论问题提供了有力帮助.利用STP方法可以将BCNs转换为标准的离散时间线性系统进行研究[8].同时在BNs和BCNs中应用STP方法也得到许多重要的结果,如稳定性[9–10]、可观测性[11–12]、可控性[13–14]、最优控制[15–16]以及同步问题[17]等.

概率布尔网络(probabilistic Boolean networks,PBNs)是Shmulevich等人于2002年提出的模型[3],该模型既具有BNs的特性,又能处理数据和模型选择中的不确定性.PBNs本质上是一类BNs的集合,其中在任意一个离散时间点,状态以一定的概率按照其中某个BN的规则转化.BCNs描述遗传调控网络的许多特征,是没有随机现象的确定性网络.概率布尔控制网络(probabilistic Boolean control networks,PBCNs)考虑了随机现象,是BCNs的一个非常有意义的扩展.在PBCNs上已经得到了许多有趣的结果,例如弱可达性[18]、可控性[19]、集稳定性[20]和输出跟踪控制问题[21]等.

可控性作为系统的一种结构性质,是系统科学和控制理论的基本概念.文献[22]研究BCNs中除禁止状态外的任意两个状态间的可控性以便更好地设计外部控制序列操纵生物系统.文献[23]研究了带有牵制控制的BCNs的可控性.文献[24]研究BCNs集成系统下的可控性,并给出判定可控性的充要条件.文献[19]讨论了开环控制和闭环控制下PBNs的可控性问题,但文献中提出的可控性准则只适用于两个确定的状态.文献[25]通过构造可达矩阵研究PBCNs的能控性和镇定性并给出相应的充要条件.文献[26]研究具有禁止状态的PBCNs的可控性.

此外,集可控性也是一个重要概念,其与一般可控性的不同之处在于,可控性表示系统可控至某个状态,而集可控性表示系统可控至某个状态集合.文献[27]首次提出BCNs的集可控性概念,并通过集可控性验证可观性,集可控性结果为文献[22]中应用结果的推广.文献[28]研究同时具有自由逻辑输入控制和网络输入控制的BCNs的可控性,并将其转换为一个集可控性问题求解.文献[29]研究切换布尔控制网络的集可控性,将集镇定问题和切换调节问题转换为集可控问题求解.文献[30]研究脉冲概率布尔控制网络(impulsive probabilistic Boolean control networks,IPBCNs)

的有限时间可控性和集可控性.文献[31]研究具有脉冲效应的布尔控制网络(Boolean control networks with impulsive effects,BCN–IE)的集可控性并以此方法解决了具有混合型控制的BCN–IE可控性和BCN–IE的输出可控性两个问题.

基于上述讨论,本文针对PBCNs集可控性问题提出两类不同的控制方法.相比于BCNs,由于状态变化的不确定性,针对PBCNs集可控性的研究更加复杂.同时与IPBCNs的集可控性研究相比,本文采取的研究方法不同.本文主要贡献如下:1)借助一个新的算子构造概率集可控矩阵,得到PBCNs在自由控制序列下集可控的充要条件;2)由该算子构造输入概率集可控矩阵,给出带有输入网络控制的PBCNs集可控的充要条件.根据已有文献,PBCNs在集可控性方面结果还很少见.

本文的其余部分安排如下:第2部分列出一些基本符号和STP的预备知识.第3部分提出PBCNs在自由控制序列和网络输入控制下的集可控问题,并给出本文的主要结果.第4部分通过数值例子验证所得结果的正确性与有效性.第5部分给出本文的结论.

2 预备知识

为了叙述方便,本文用到的相关符号如下列出:

1)Mm×n:m×n维矩阵集合.

2) Col(A):矩阵A的列集合.Coli(A):矩阵A的第i列.

7)Ξm:={1,2,···,2m}.

8)α:从Ω=[0,1]取值的随机布尔变量.定义Λ={[α1−α]T|α ∈Ω},表示α为向量形式.

9) 矩阵A ∈Mm×n的列元素由Λm组成,称矩阵A为随机逻辑矩阵.:m×n维随机逻辑矩阵集合.

11) 矩阵A=(Aij),B=(Bij)∈Mm×n,定义

则A ∨B=(Aij ∨Bij).

12)Bm×n:m×n维布尔矩阵集合.

定义1[6]矩阵有A ∈Mm×n,B ∈Mp×q,t=lcm(n,p)是{n,p}的最小公倍数.矩阵A,B的半张量积记为

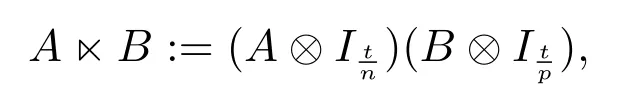
其中⊗表示Kronecker积.

注1STP是普通矩阵乘积的推广.在下文无混淆情况下,可省略“”.

设x为逻辑变量,即x ∈D.用向量表示逻辑值的结构,分别表示为即有D∼∆2和其中∼表示同一事物的两种不同表示形式.

引理1[6]设f(x1,x2,···,xn)为一个逻辑函数,在向量形式下f:Dn →D,存在唯一的逻辑矩阵Mf∈称为f的结构矩阵,使得

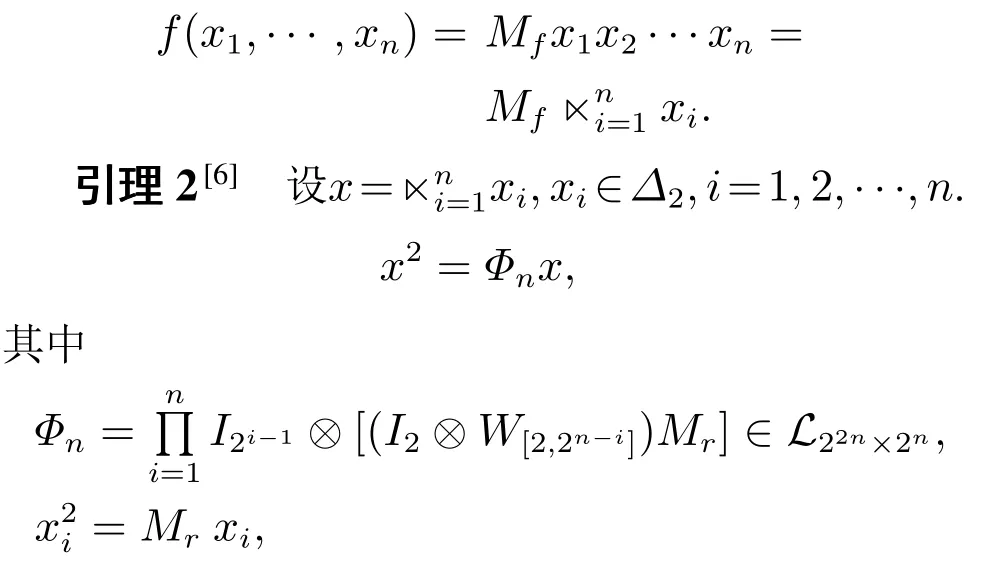
其中Mr=δ4[1,4]为降阶矩阵.

3 主要内容

首先给出PBCNs的代数表示,其次考虑在自由控制序列下PBCNs的集可控性问题,最后考虑输入网络控制下PBCNs的集可控性问题.

3.1 PBCNs的代数表示

其中:xi(t)和uj(t)∈D,i=1,2,···,n,j=1,2,···,m是逻辑状态和输入控制状态;fi:Dm+n →D是逻辑函数;t=0,1,···,是离散时间.

注2在本文中,考虑的概率布尔控制网络是独立的,则意味着f1,f2,···,fn是独立的,即有

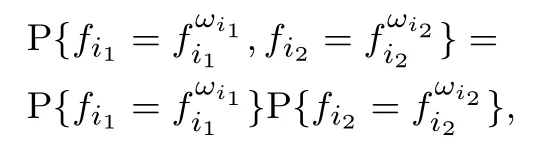
其中i1i2,i1,i2∈{1,2,···,n}.

3.2 PBCNs的集可控

由式(3)可知

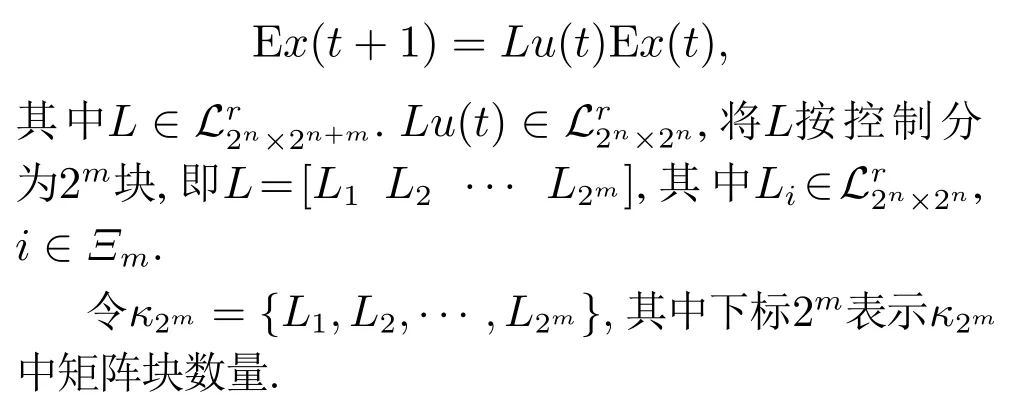
定义运算符⟨·⟩为

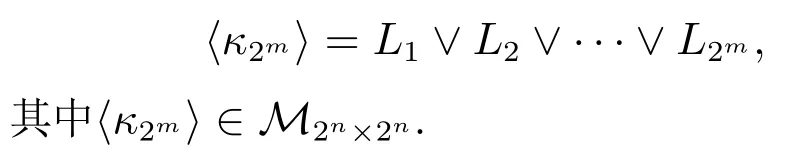
定义

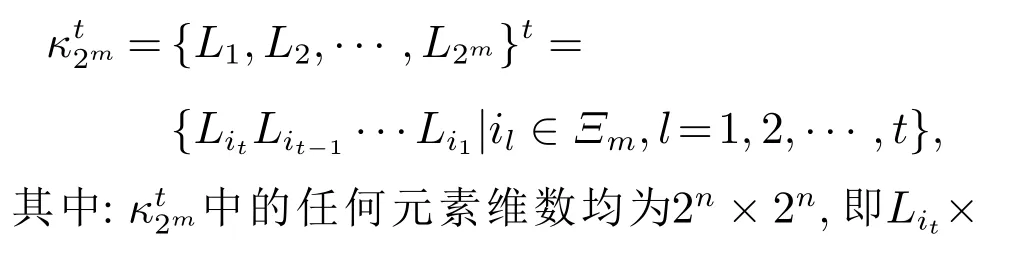
首先给出系统(1)可控的定义.

定义2考虑PBCNs,设初始状态x0∈和目的状态xd∈

1) 若存在一个自由控制序列{u(0),u(1),···,u(t−1)}使P{xd=x(t)|x0=x(0)}=1成立,则称xd是从初始状态x0在t时刻依概率1可控的.

2)t时刻概率1可达集是指从初始状态经时间t依概率1可达的状态集合,记为Rt(x0).概率为1的整体可达集是指从初始状态依概率1可达的状态集合,记为R(x0).

根据上述定义以及概率可控矩阵可得以下定理.

定理1考虑具有自由控制序列的PBCNs系统(1),其对应概率可控矩阵C=(Cij),则

证x(t+1)的期望值Ex(t+1)满足

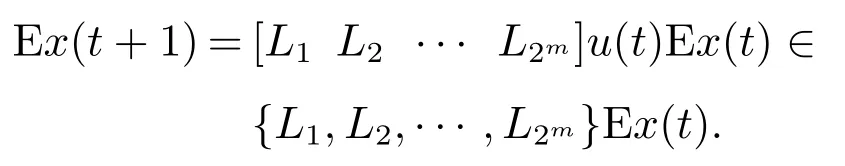
直接计算可得

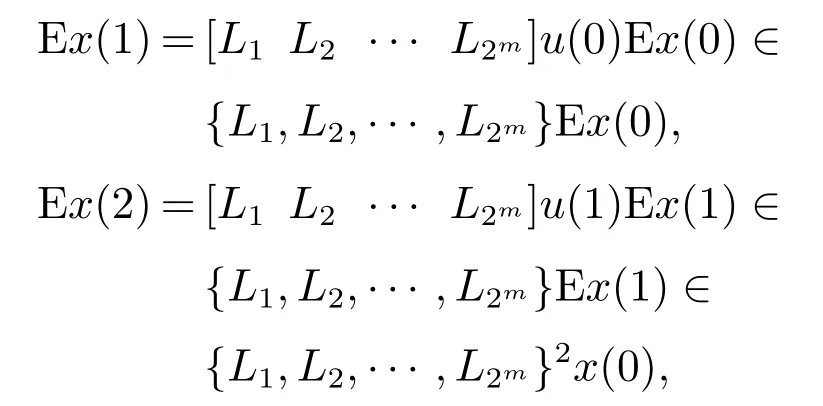
重复上面迭代过程,可得

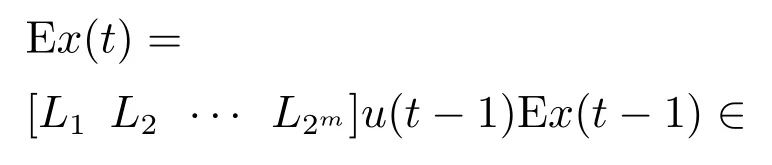
其控制序列使得系统(1)从初始状态x0依概率1可达目的状态xd.因此至少存在一种由自由控制序列使系统(1)从初始状态x0依概率1可达目的状态xd.同时回顾运算符⟨·⟩的定义,则可化简得

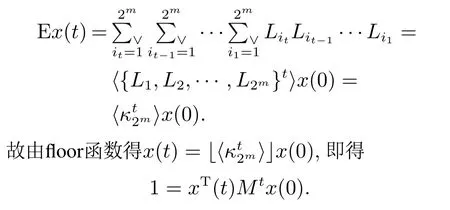
在系统(1)中必存在一条由初始状态x0在第t步依概率1可达目的状态xd的路径.即有

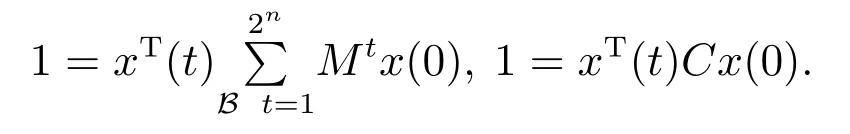
故系统(1)中必存在一条由初始状态x0依概率1可达目的状态xd的路径.

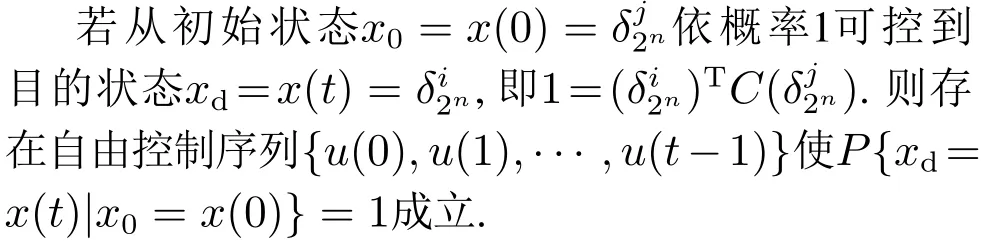
同理可证式(2)和式(3)成立. 证毕.

为了考虑集可控性问题,首先引入指标列向量给定系统(1)的初始指标矩阵和目的指标矩阵.

现给定一个具有n个结点的PBCNs.状态集表示为N={1,2,···,2n},令s∈2N,s是给定的状态集合,引入指标列向量V(s)=[(V(s))1(V(s))2···刻画s的特征,其中

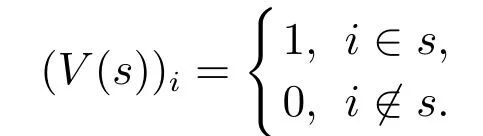
PBCNs的初始集族为P0和目的集族为Pd,可表示为

由指标列向量将初始集族P0和目的集族Pd定义为初始指标矩阵J0和目的指标矩阵Jd,即

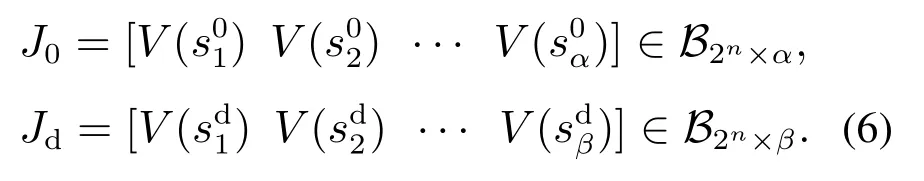
由式(5)–(6)定义矩阵,称为概率集可控矩阵.即

定义3具有初始集族P0和目的集族Pd的系统(1).满足

根据上述定义以及概率集可控矩阵得以下定理.

定理2具有初始集族P0和目的集族Pd的系统(1).其相应的概率集可控矩阵为Cs=(Cs)ij,则

3) 系统(1)依概率1集可控当且仅当Cs=1β×α.

证必要性.考虑初始指标矩阵J0和目的指标矩阵Jd.概率可控矩阵C的定义为

由概率集可控矩阵Cs的定义可知

充分性.由概率集可控矩阵Cs知

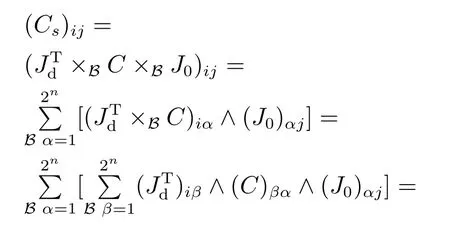
同理可证(2)和(3)成立. 证毕.

3.3 输入PBCNs的集可控

在本节中,将系统(1)中的控制看作是满足一定逻辑规则的逻辑变量,称为输入网络.如下所示:

定理3考虑具有输入网络的PBCNs系统(1),其对应输入概率可控矩阵D=(Dij),则

重复上面迭代过程,可得

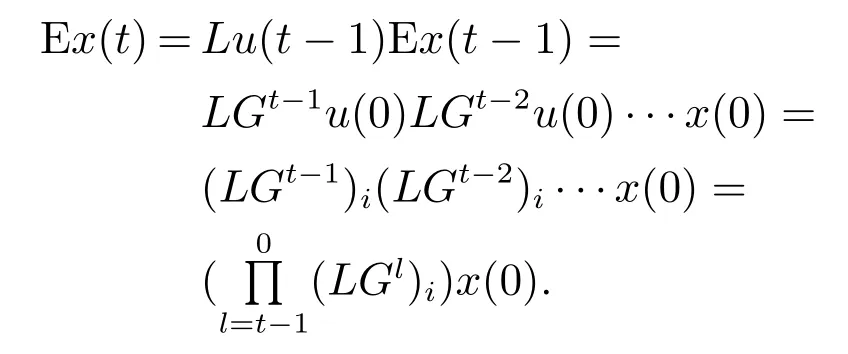
因此,可以获得以下方程

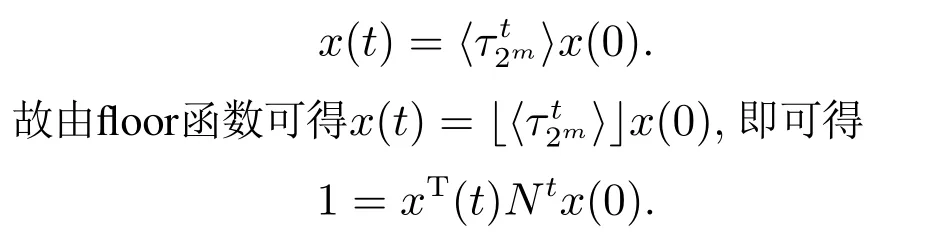
在系统(1)中存在由初始状态x0在第t步依概率1可达目的状态xd的路径,即

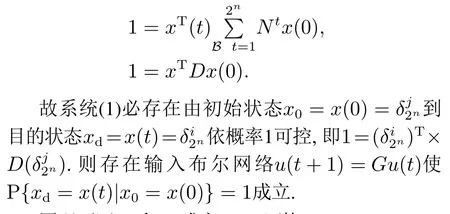
同理可证(2)和(3)成立. 证毕.

根据式(6)和式(9)定义矩阵,称为输入概率集可控矩阵,即有

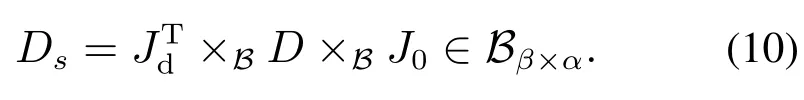
定理4具有初始集族P0和目的集族Pd的系统(1),其输入概率集可控矩阵为Ds=(Ds)ij.则

3) 系统(1)依概率1集可控当且仅当Ds=1β×α.

由于定理4与定理2证明是类似的,均通过构造相应的可控矩阵,对系统(1)集可控性进行判定,证明思路相似,因此定理4的证明略去.

4 算例分析

在本节中,使用文献[19]中的例子来验证前面提出的定理2和定理4.

例1考虑自由控制序列下PBCNs的集可控性.

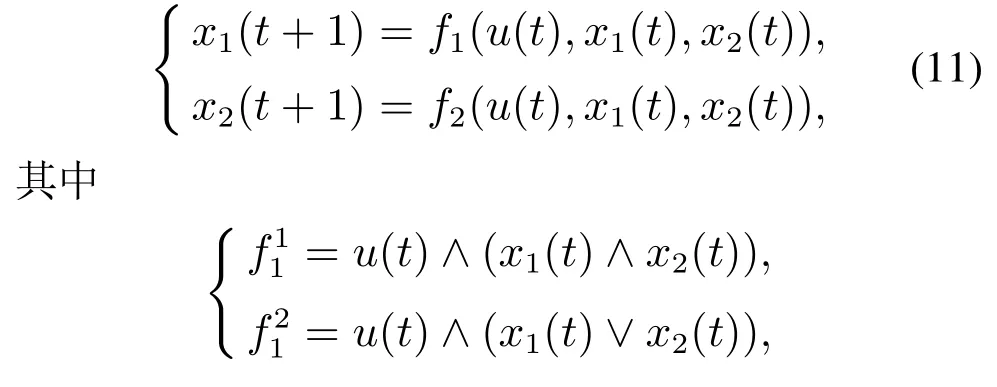
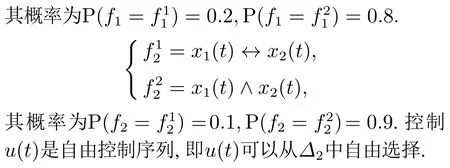
模型指标矩阵K和对应模型概率为

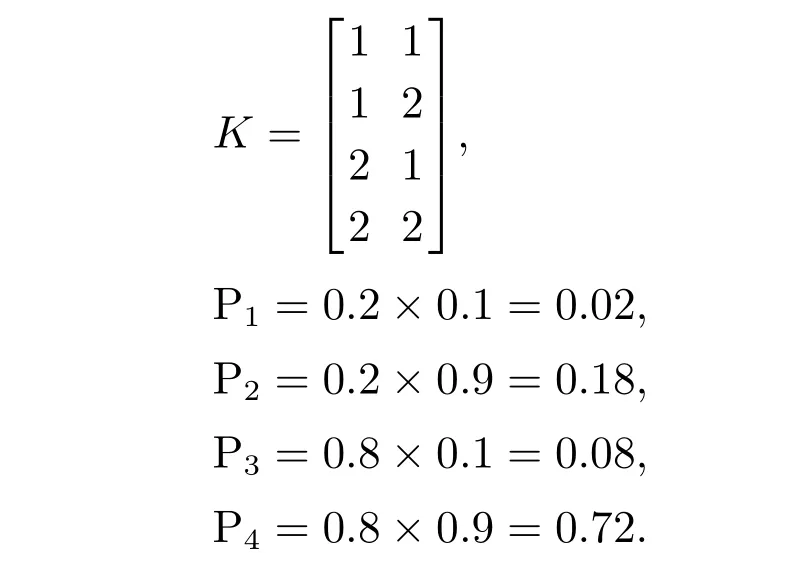
设x(t)=x1(t)x2(t),则各网络的网络转移矩阵可按标准程序计算.对于第1个模型,有

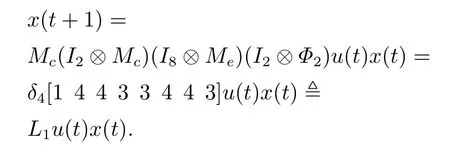
其中Mc和Me可由文献[7]得.同样地,L2,L3,L4可计算得

则可得

由计算可得t=2n,t=1,2,3,4.当t=1时,

当t=2,3,4时,

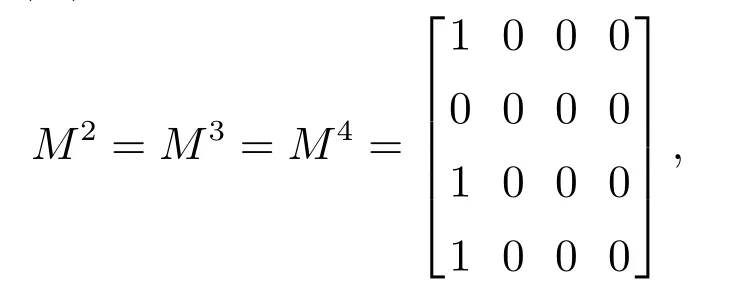
则可得概率可控矩阵

假设初始集族P0和目的集族Pd为

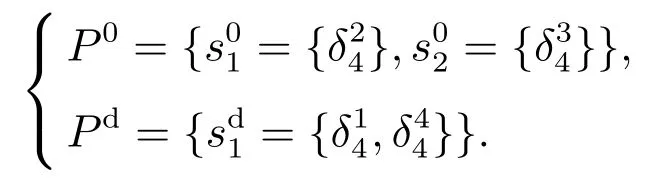
其相应指标矩阵为

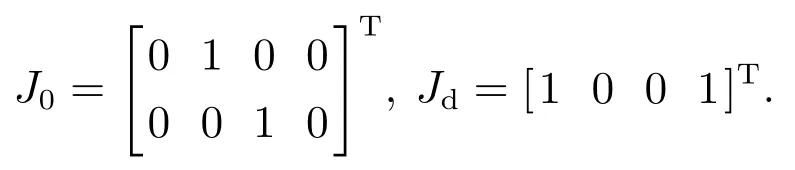
则可得概率集可控矩阵

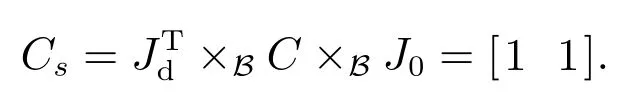
故在自由控制序列下的系统(11)在初始集族P0和目的集族Pd下集可控.

例2考虑输入网络控制下PBCNs的集可控性,

其中

其控制网络u(t)=u1(t)u2(t)可得结构矩阵为G=δ4[4 3 2 1].

各网络的网络转移矩阵按标准程序计算可得

由计算可得t=2n,t=1,2,3,4.当t=1时,

当t=2时,

当t=3,4时,

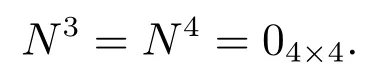
则可得输入概率可控矩阵

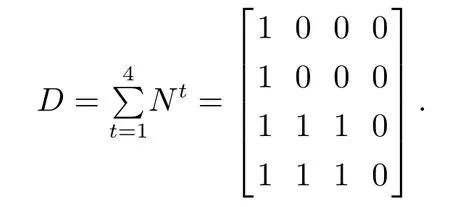
在例1的初始集族P0和目的集族Pd下可得输入概率集可控矩阵

故在输入网络控制下的系统(12)在初始集族P0和目的集族Pd下集可控.

5 结论

本文研究了PBCNs的集可控性问题.基于矩阵半张量积方法给出PBCNs的代数表示.基于该代数表示,借助新的算子构造出概率集可控矩阵和输入概率集可控矩阵.利用概率集可控矩阵给出了在自由控制序列下PBCNs集可控性的充要条件,并根据输入概率集可控矩阵得到了在网络输入控制下PBCNs集可控性的充要条件.