多型岸舰导弹作战单元部署优化模型

宋贵宝，姜子劼，刘战，刘镇毓

(海军航空大学, 山东 烟台 264001)

0 引言

岸舰导弹部队是海军岸防部队的主要兵种之一，是国家海防体系的重要构成部分[1]，担负着扼守海峡、保卫交通、抗登陆作战等重要使命任务。岸舰导弹的战术运用以灵活、隐蔽、分散等原则为指导，“根据敌方舰船活动情况，将岸舰导弹作战单元机动至最佳位置，然后捕捉时机突然攻击”是当前普遍采用的作战样式[2-3]。因此科学合理地将各型岸舰导弹作战单元部署至有利于作战的攻击位置，可以保障岸舰导弹的技战术性能得到最大限度的发挥。

现阶段对于岸舰导弹作战单元优化部署的相关研究多以发射阵地的优化选择为主：孟伦等[4]分析了作战意图、射程因素、地形及交通因素、安全性因素等影响岸舰导弹发射阵地选择的主要因素，针对指标间相互冲突不可公度的问题运用熵值原理确定指标熵权系数作为指标客观权重，反映了各指标在竞争意义上的相对激烈程度，并采用层次分析法引入决策者的主观权重，将主、客观权重相结合确定各指标综合权重。唐培锋等[5]从岸舰导弹技战术性能和战术运用两个方面进行考虑，提出兵力突击条件、兵力机动条件、兵力防护条件、通信指挥条件等影响岸舰导弹发射阵地选择的具体因素，并运用层次分析法(AHP)方法确定了指标权重，运用模糊评判技术得到了优选阵地。上述研究以现代模糊多属性决策理论为基础，既考虑了影响阵地选择决策的多种因素，又解决了具有不同度量单位和相互冲突目标的多目标决策问题，但并未考虑技战术性能与战术运用各异的岸舰导弹配置于所选阵地时发挥着不同的战术作用。

为了适应未来战争多军兵种高度协同等新特点，岸舰导弹将逐渐具备对重要海峡、航道和一定海域的控制能力。为了实现该能力，兵力突击条件越来越成为岸舰导弹作战部署的关键因素。具备兵力突击条件，就是根据目标舰船可能途经海域部署岸舰导弹作战单元，确保火力能够有效覆盖相关海域活动的目标舰船[4]。出于这一考虑，本文将岸舰导弹部署问题与覆盖选址问题联系起来。

在多个领域中的实践已经证明，最大覆盖选址问题(MCLP)模型是目前解决设施选址问题的最有效模型之一[6-10]。MCLP是运筹学中的经典问题，研究如何在给定设施数量的条件下，运用科学的方法决定设施的地理位置，使各个服务节点的服务需求得到满足。但该模型因基于“节点要么被覆盖，要么不被覆盖”的二元覆盖度假设提出，所以无法反映岸舰导弹作战单元部署中“目标点被各型岸舰导弹作战单元重复覆盖”的真实情况。

Berman等[11]在MCLP基础上将覆盖度扩展为多元形式，提出部分覆盖观点以及广义最大覆盖选址问题(GMCLP)。GMCLP考虑了每一个节点都可能会被多个设施以不同程度覆盖的情况，与岸舰导弹作战单元部署问题更为接近。但与GMCLP相比，岸舰导弹作战单元部署问题仍然有其自身的特殊性：

1)在服务区域上，GMCLP通常采用固定服务半径的形式，服务区域形状为标准圆，在部分研究中，服务水平随服务距离的增加而呈阶梯或连续减退；而岸舰导弹作战单元的服务区域受到射向、射击扇面、最小与最大射程等技术性能影响，存在服务角度和最小、最大服务半径。目前尚无对该区域的数学解析公式及相关研究。

2)在节点问题上，GMCLP通常将服务空间网格化，将网格点作为服务节点，而岸舰导弹作战单元的服务节点需要根据目标舰船在相关海域的运动情况，按照一定的规则和方法分析计算。

3)在覆盖程度上，GMCLP较少对服务节点的受覆盖程度施加约束，而为了保证在其射击区域内大量毁伤敌方舰船，岸舰导弹作战单元部署问题应当对服务节点的受覆盖程度施以约束。

针对有效覆盖和打击目标舰船的主要作战任务，考虑到岸舰导弹作战单元部署问题的特殊性，本文建立了基于GMCLP的多型岸舰导弹作战单元部署优化模型以及岸舰导弹火力覆盖区域计算模型、目标散布区域计算模型，并针对模型特征设计了优化算法，通过算例仿真初步表明了模型的有效性，可以为多型岸舰导弹作战单元部署优化决策提供支撑。

1 问题分析

岸舰导弹作战单元部署优化决策，即根据发射阵地位置，目标舰船可能途经海域，各型岸舰导弹的覆盖范围、战术性能，岸舰导弹部队的兵力条件，将各岸舰导弹作战单元合理地配置于预设阵地并确定基准射向，对目标舰船实施有效打击。

在各阵地展开面积、地形、视界及各类设施大致相同的条件下，影响岸舰导弹作战单元部署决策的主要因素有：

1)发射阵地位置。发射阵地是岸舰导弹作战单元展开战斗队形，进行战斗准备和实施导弹发射的地域，一般分布在具有良好视场和发射角度的地带。发射阵地与目标点的相对位置关系，决定岸舰导弹作战单元能否对目标实施有效打击。

2)目标散布区域。目标散布区域是根据目标舰船初始位置、航向、航速等信息推算得到的若干目标位置散布点的集合，目标位置散布点由目标当前位置、目标机动时间及目标机动散布规律共同决定，是岸舰导弹作战单元服务的主要对象。

3)各型岸舰导弹的火力覆盖区域及预定射向。岸舰导弹火力覆盖区域是岸舰导弹以预定射向发射，以一定精度命中并毁伤目标舰船位置点的集合，该区域是由远界、近界以及左右边界围成的封闭图形，也是岸舰导弹在其作战单元部署问题中的服务区域。

4)各型导弹的战术性能。出于毁伤目标舰船的首要战术考虑，毁伤能力可认为是岸舰导弹的主要战术性能指标。

5)岸舰导弹部队的兵力条件。在实际战场条件下，战场资源通常会成为武器部署的重要约束[12]。

2 模型建立

2.1 目标散布区域计算模型

假设海上目标航行距离较远且不考虑海浪运动、地球曲率等影响，可将其视为在水平面内运动的质点。若预先获得目标初始位置，目标航速、航向等诸元，可基于上述诸元的散布规律，利用蒙特卡洛法模拟生成若干处目标散布点作为岸舰导弹作战单元服务对象。

2.1.1 目标初始位置

目标初始位置是指岸舰导弹作战单元展开部署前由侦察预警平台最后一次获取的目标舰船位置信息。由于侦察预警平台对海上目标定位存在误差，目标初始位置(xi,yi)一般服从以目标定位点(xt,yt)为圆心，以定位误差σP为均方差的二维正态圆散布[13-14]，其概率密度函数为f(xi,yi)，即

(xi,yi)～f(xi,yi)=

(1)

2.1.2 目标机动时间

目标机动时间是指岸舰导弹作战单元展开部署前最后一次获取目指信息时刻到岸舰导弹飞行自控终点时刻的时间，可分为2个阶段：一是最后一次获取目指信息时刻到各岸舰导弹作战单元完成部署接收攻击指令时刻；二是接收攻击指令时刻至岸舰导弹飞行自控终点时刻。为了统一计算，规定各岸舰导弹作战单元接收攻击指令后采取先后进行发射的方式保证岸舰导弹同时或以较小的时间间隔到达飞行自控终点，那么对于不同岸舰导弹作战单元，目标机动时间可视为常量，设为tT.

2.1.3 目标机动散布规律

目标机动散布包括目标航速散布和目标航向散布，在侦察预警平台提前测定目标概略航速(包括目标最小航速vmin和最大航速vmax)和概略航向(包括航向角分布范围Δω和主航向角ωM)的条件下，若在岸舰导弹发射前，目标舰船未能获取岸防兵力的有关动向并进行转向等机动规避措施，可假定目标舰船航速vt和航向ωt分别服从概略航速正态分布和概略航向正态分布[14-16]，即

vt～g(vt)=

ωt～h(ωt)=

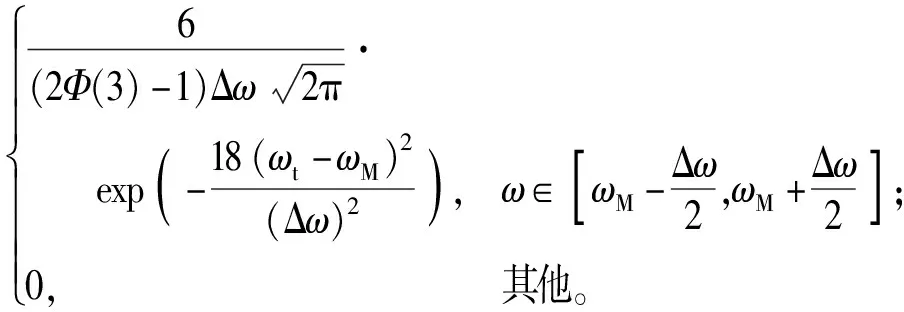
(2)

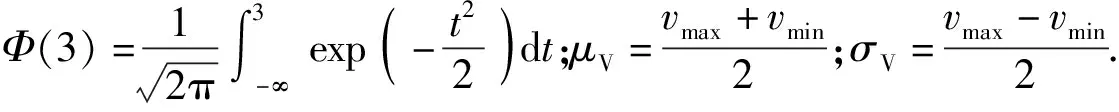
通过蒙特卡洛仿真法，生成服从(1)式分布的若干(xij,yij)，服从(2)式分布的若干vtj、ωtj，其中(xij,yij)、vtj、ωtj分别为第j次蒙特卡洛仿真中生成的目标初始位置、目标舰船航速和目标舰船航向，则根据运动方程，第j个海上目标位置散布点(简称目标散布点)Tj(xTj,yTj)应满足：

(3)

2.2 岸舰导弹火力覆盖区域计算模型

影响岸舰导弹火力覆盖区域远界、近界以及左、右边界的主要因素有岸舰导弹最大射击扇面角、最小射程和最大有效射程等，现将分别分析上述因素的影响方式，并在此基础上给出岸舰导弹火力覆盖区域各边界的数学解析式。

2.2.1 岸舰导弹火力覆盖区域边界

扇面发射，是指通过装定射击扇面角，控制导弹发射后机动转弯，使导弹转弯后的前置航向对准目标点的发射方式。在一定角度范围内，导弹采取扇面发射可以保证导弹的飞行稳定性，但超过该角度范围，随着射击扇面角ω的增大，弹道参数会逐渐恶化[17]，进而影响导弹的射击精度，称该角度范围为导弹最大射击扇面角。为了保证导弹的飞行稳定性和射击精度，规定导弹最大射击扇面角Θ作为其火力覆盖区域的边界，即ω∈[-Θ,Θ]。

2.2.2 岸舰导弹火力覆盖区域近界

岸舰导弹的最小射程是导弹以一定射击精度命中的目标点与发射点之间的最小水平距离[18]，文献[19]通过仿真实验证明了在各个射击扇面角上，岸舰导弹的最小射程都是不同的，基于这一结论，通过分析导弹飞行的纵向运动和侧向运动，提出岸舰导弹最小射程的一种估计方法。

导弹以倾斜角φ发射后在助推器作用下沿着发射方向加速爬高至h0，由于导弹发射转入稳定飞行后导引头才能开机工作，因此需要从导弹飞行的纵向和侧向两个方面分析其飞行的水平距离。

在侧向上，助推器分离后，导弹开始扇面转弯(设转弯时导弹沿其速度的侧向分量方向受到的阻力和动力相等，转弯半径r按助推器分离时的速度v计算)至前置航向对准目标点，转弯结束，导引头最早可在此时开机，该过程如图1所示。图1中O为发射点，D为助推器分离点，C为转弯圆心，F为扇面转弯终点，T为目标点。

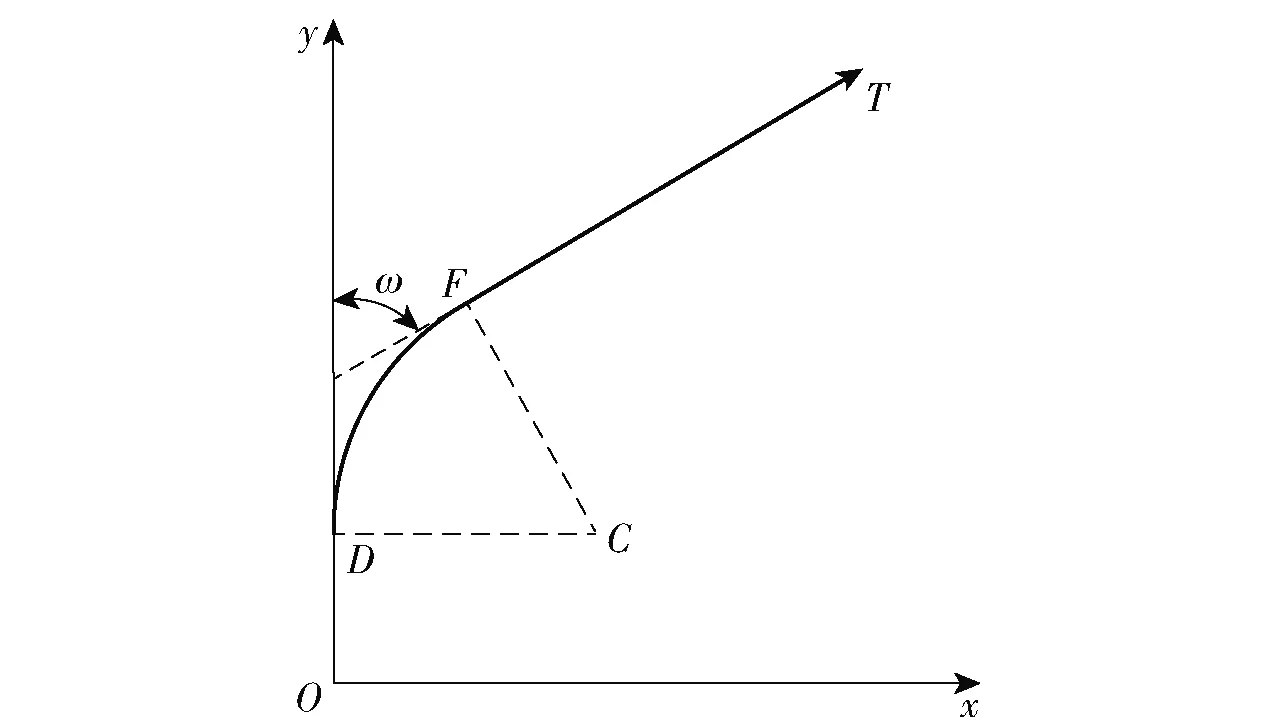
图1 导弹侧向运动轨迹示意图

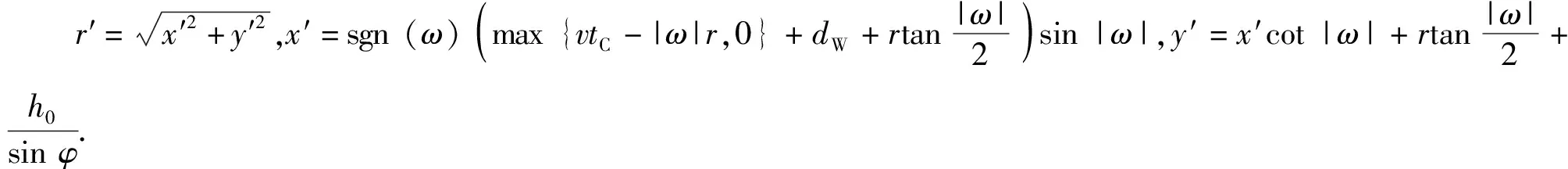
导弹火力覆盖区域近界即为(x′,y′)在其定义域ω∈[-Θ,Θ]内的轨迹。

取Θ=90°，φ=20°，r=60 km，dW=60 km，h0=500 m，v=400 m/s，tC=1.25 min，仿真得到不同射击扇面角下导弹的最小射程如图2所示。由图2可以看出：当射击扇面角小于0.16π rad时，导弹完成扇面转弯时仍未转入平飞，导弹最小射程主要受纵向运动影响，随射击扇面角变化不大；当射击扇面角大于0.16π rad时，导弹完成扇面转弯前已转入平飞，通过的水平距离随射击扇面角的增加而增大，最小射程随之增加，与文献[19]仿真实验结果一致。

图2 最小射程变化示意图

2.2.3 岸舰导弹火力覆盖区域远界

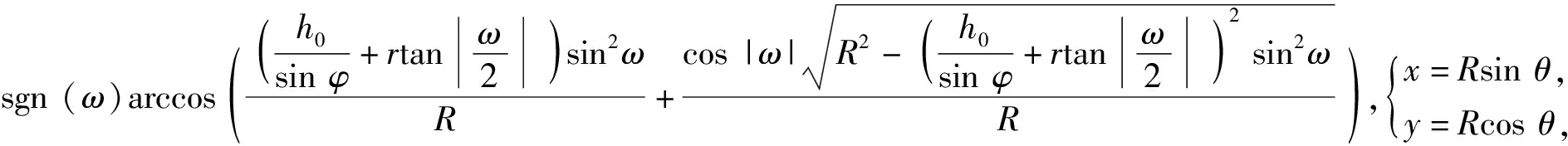
2.2.4 某型岸舰导弹火力覆盖区域仿真

取R=300 km，发射点为原点，基准射向为y轴正方向(箭头所指方向)，其他参数同2.2.2节中仿真参数，仿真得到岸舰导弹火力覆盖区域如图3所示。该区域是一个近似扇环的封闭图形，内环半径(即最小射程)已由图2示出，外环半径大小为R.

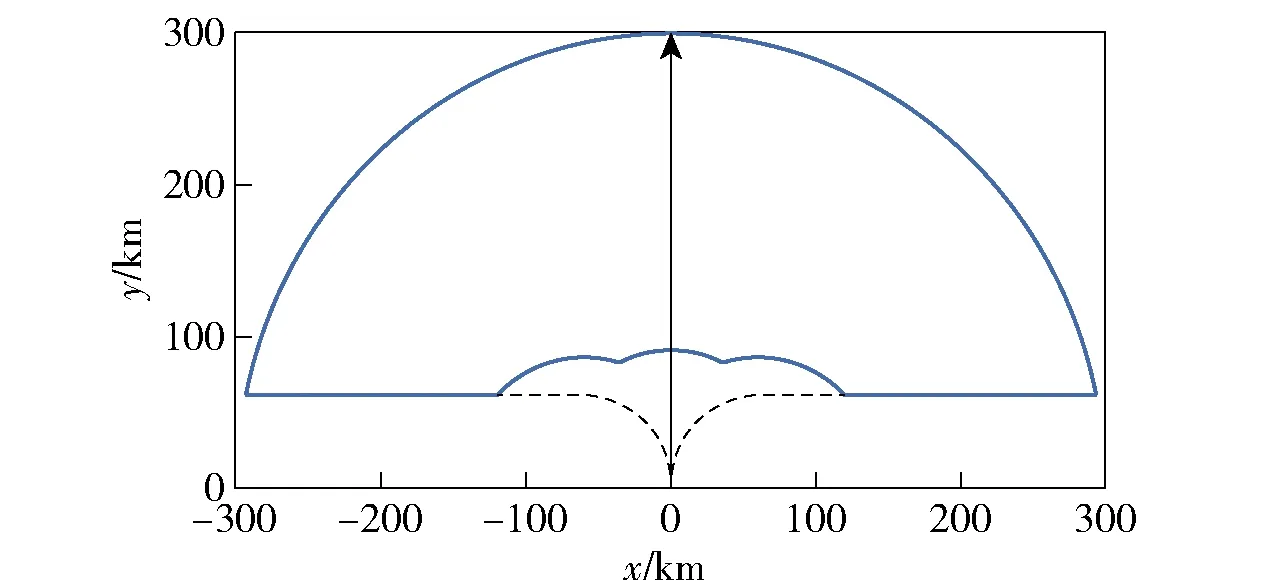
图3 岸舰导弹火力覆盖区域仿真图

2.3 基于GMCLP的多型岸舰导弹作战单元部署优化模型

2.3.1 问题描述

某岸舰导弹部队装备有m种不同型号的岸舰导弹作战单元，其中可投入作战使用的各型岸舰导弹作战单元数量为Mk. 根据侦察预警平台测定的目标舰船位置、航速、航向等目标指示信息，按照2.1节中的方法模拟生成了N处目标散布点，Tj(xTj,yTj)为其中第j个目标散布点，现以使各目标散布点毁伤值之和最大为目标，向n个预选阵地中的部分阵地展开部署Pi(xi,yi)为其中第i个预选阵地，要求确定部署于阵地Pi的岸舰导弹作战单元型号ci以及部署于Pi的岸舰导弹作战单元的基准射向与地面参数坐标系y轴正方向的夹角βi，其中，ci∈{0,1,2,…,m},i∈{0,1,2,…,n}，βi∈[0 rad,2π rad]，若不在Pi部署岸舰导弹作战单元，则ci=0.

2.3.2 模型假设

为了形成多层次、交叉重叠的火力网并满足各阵地的展开条件，要求各岸舰导弹作战单元分散配置，规定每个发射阵地仅部署一型岸舰导弹作战单元。

在一批打击中，岸舰导弹作战单元中的数个发射单元基准射向相同。

2.3.3 毁伤值Sj

在岸舰导弹作战单元部署问题中，目标舰船在各目标散布点受到不同岸舰导弹作战单元的覆盖并遭到不同程度的毁伤。为了评估目标舰船在各目标散布点的受毁伤程度，定义目标舰船在Tj的毁伤值Sj为无对抗条件下目标舰船在Tj受到的联合毁伤概率，即

(4)

式中：0-1变量aij为Tj是否在部署于Pi的岸舰导弹作战单元的火力覆盖区域内，aij=1时，Tj在部署于Pi的岸舰导弹作战单元的火力覆盖区域内，aij=0时，Tj不在部署于Pi的岸舰导弹作战单元的火力覆盖区域内；pci为无对抗条件下，部署于Pi的岸舰导弹作战单元对目标舰船的毁伤概率。

式中：σT——试验器脉动循环最大应力；σW——标准循环下考核点最大应力；σb,W——标准循环下材料的极限拉伸强度；σb,T——试验器温度下材料的极限拉伸强度。

2.3.4 确定变量aij

基于2.2节提出的岸舰导弹火力覆盖区域各边界解析式，给出变量aij的计算步骤：

1)坐标转换。将目标散布点Tj(xTj,yTj)由地面参数坐标系转换至以阵地Pi(xi,yi)为原点，以部署于该阵地岸舰导弹作战单元的基准射向为y轴正方向的平面直角坐标系内：

(5)

(6)

式中：vci为ci型岸舰导弹稳定飞行速度的侧向分量；rci为ci型岸舰导弹在速度vci下的最小转弯半径；h0ci为ci型岸舰导弹开始扇面转弯时的飞行高度；φci为ci型岸舰导弹的发射倾斜角。

3)计算目标散布点与发射点的直线距离：

(7)

4)判断取值。若Tj能够被部署于Pi的岸舰导弹作战单元火力覆盖，则Tj应满足：

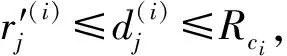
则变量aij满足：

(8)

2.3.5 目标函数

使各目标散布点毁伤值之和f最大，即

(9)

2.3.6 约束条件

为了保证各岸舰导弹作战单元能够尽可能地对其有效射程以内的目标舰船造成毁伤，施加约束条件：与发射阵地的直线距离不大于部署于该阵地岸舰导弹作战单元最大有效射程的目标散布点所受毁伤值不小于该岸舰导弹作战单元的毁伤概率，即

(10)

式中：ε(·,0)为单位阶跃函数，

为了使战场资源得到充分利用，规定部署于各阵地的某型岸舰导弹作战单元数量之和应等于能够投入作战的该型岸舰导弹作战单元总数，即

(11)

2.3.7 建立优化模型

3 算例分析

为了验证该模型可以有效支撑岸舰导弹作战单元部署的战场决策，设计想定战场并进行优化分析。

3.1 战场想定

红方预警平台侦测到3处疑为蓝方战斗编队的海上目标向红方海域航行，3处目标的目指信息如表1所示。

表1 目标指示信息表

红方某岸舰导弹部队装备有A、B两型岸舰导弹作战单元，其中可投入作战使用的有A型3个、B型2个，两型导弹的技战术指标如表2所示。

表2 导弹技战术指标表

有7处预设阵地可供红方岸舰导弹部队部署选择，阵地坐标如表3所示。

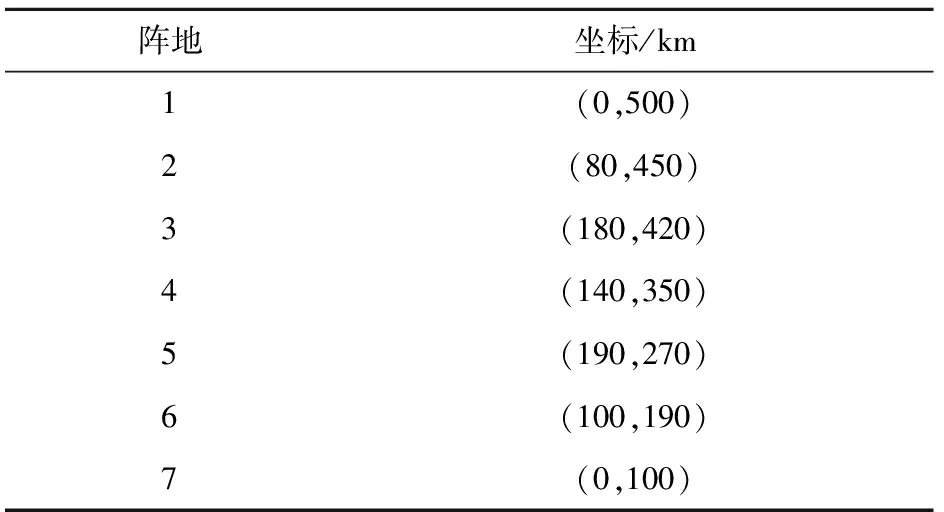
表3 预设阵地坐标表

3.2 仿真方法及结果

本文以MATLAB软件为主要仿真软件，以粒子群算法为主要优化方法。

1)根据(1)式、(2)式、(3)式与表1所给目指信息，取tT=1 h，模拟生成了共100处目标散布点，散布点与各预设阵地坐标如图4所示。

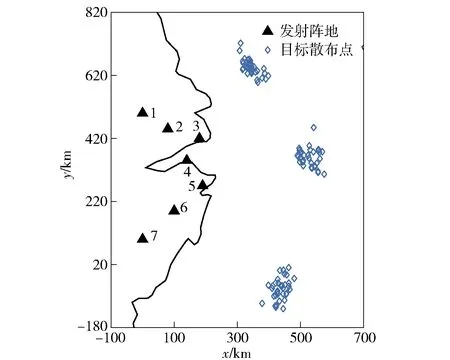
图4 预设阵地、目标散布点示意图

2)设计粒子群算法进行优化。

步骤1输入算法参数：种群规模popsize，最大进化次数maxgen，学习因子c1、c2，最大、最小速度vmax、vmin，最大、最小惯性权重wmax、wmin；粒子编码机制采取一维向量编码，即

x=[c1,c2,…,cn,β1,β2,…,βn].

步骤2种群初始化：

①按照如下方式随机生成粒子初始位置：在第l个粒子中，第i个阵地部署的岸舰导弹作战单元型号x(i,l)在0和岸舰导弹作战单元型号数量m之间取随机整数产生，基准射向x(i+n,l)在[0 rad,2π rad]内取随机数产生，即

fori=1:n

forl=1:popsize

x(i,l)=randi([0m]);

x(i+n,l)=sgn(x(i,l))×rand×2π;

end

end.

②为了避免部署的x(i,l)型岸舰导弹作战单元数量超过可用的x(i,l)型岸舰导弹作战单元数量Mx(i,l)，按照如下方式修正初始粒子位置：当第l个粒子中部署的x(i,l)型岸舰导弹作战单元总数超过了可用的x(i,l)型岸舰导弹作战单元数量Mx(i,l)时，对x(i,l)重新赋值，直到x(i,l)型岸舰导弹作战单元总数恰好等于可用的x(i,l)型岸舰导弹作战单元数量，即

while sum(x(1:n,l)==x(i,l))>Mx(i,l)

x(i,l)=randi([0m]);

end.

(12)

③随机生成粒子初始速度。

步骤3将约束条件(10)式转化为目标函数惩罚项，惩罚系数M取为一较大正数，即

(13)

根据(13)式计算各粒子适应度fitness(l)，选出个体极值和全局极值。

步骤4若当前进化次数小于最大进化次数maxgen，则执行步骤5～步骤7，否则转步骤8.

步骤5粒子速度更新：第j个粒子的第i维的速度按照(14)式更新：

v(i,l)=w(l)v(i,l)+c1r1(Pb(i,l)-x(i,l))+

c2r2(Gb(i)-x(i,l))，

(14)

式中：Pb(i,l)为第l个粒子个体极值的第i维；r1、r2为闭区间[0,1]内的随机数；Gb(i)为全局极值的第i维；w(l)是惯性权重，采用自适应惯性权重法：当第l个粒子的适应度fitness(l)小于种群平均适应度时，其惯性权重较大，有利于粒子跳出局部最大值，进行全局搜索；反之其惯性权重较小，有利于其对当前区域进行精细的局部搜索。

步骤6粒子位置更新与粒子位置修正。按照(15)式更新粒子位置，并令超过边界约束粒子的对应维停靠在该维的边界上：

(15)

式中：round(·)为四舍五入函数。

当第l个粒子中部署的x(i,l)型岸舰导弹作战单元总数超过了可用的x(i,l)型岸舰导弹作战单元数量Mx(i,l)时，按照(12)式进行修正。

步骤7按照(13)式计算各粒子适应度fitness(l)，并更新个体极值和全局极值。

步骤8输出全局极值。

3)设种群规模为10，最大进化次数为200，独立运行算法10次，得到最优解目标函数值分布情况如图5所示。取一组最优值最大的最优解(见表4)作为最终方案进行部署，得到各岸舰导弹作战单元基准射向、火力覆盖区域和各目标散布点毁伤值如图6所示。

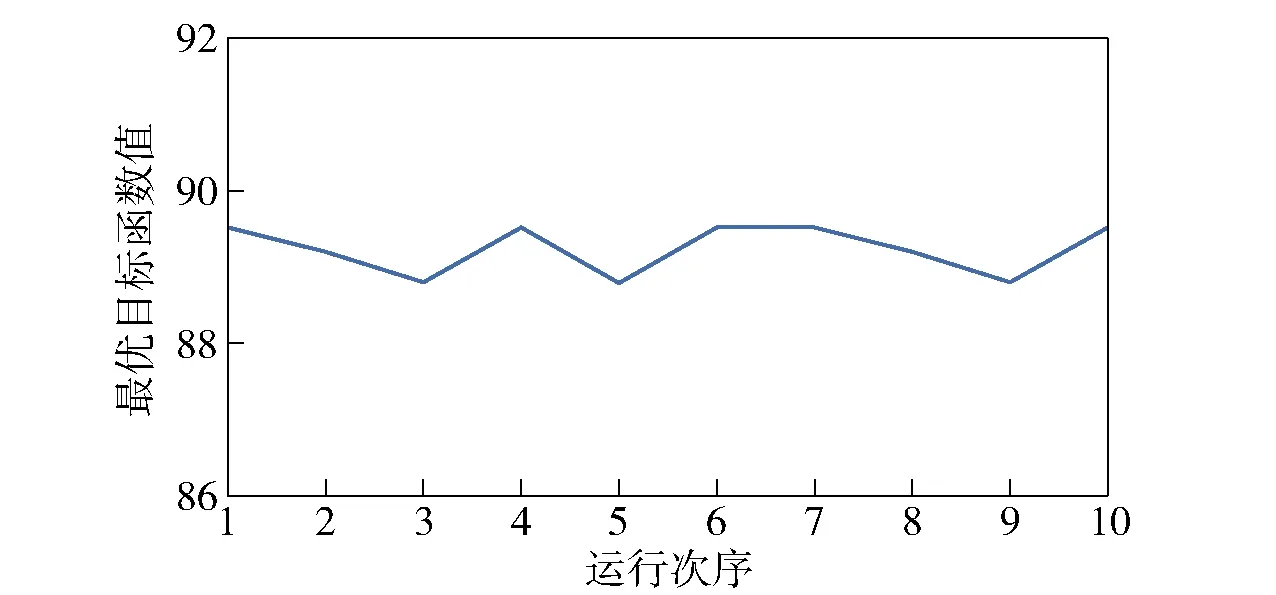
图5 最优值分布

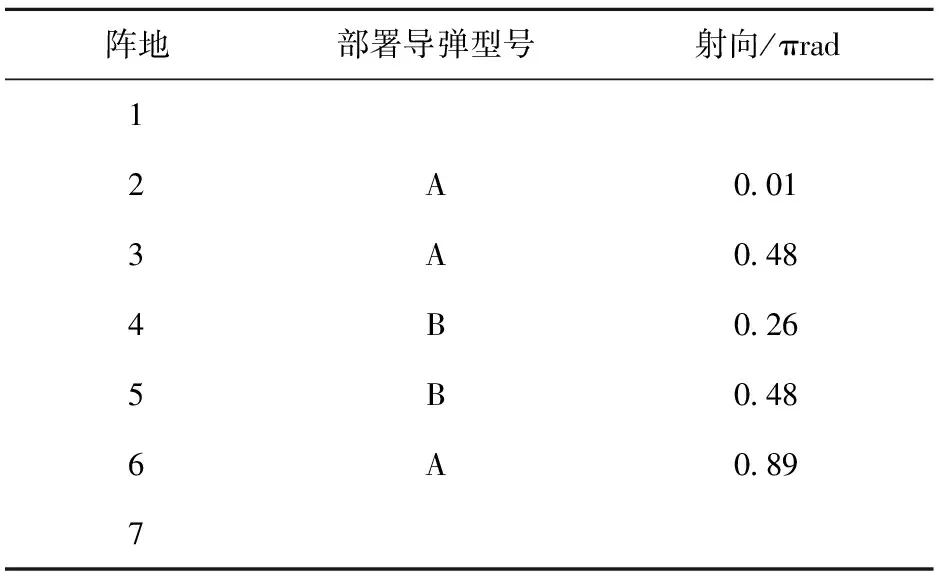
表4 最优解

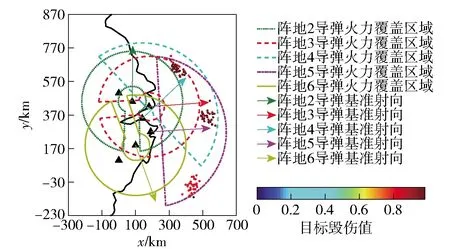
图6 岸舰导弹部署示意图

3.3 仿真结果分析

为了判断上述结果是否为本问题唯一的最优解，加入外部档案(全局极值的集合，每一次迭代中适应度为全局极值适应度的粒子进入外部档案，若全局极值更新，则删除外部档案中的粒子，仅保留新的全局极值)再次进行仿真实验，发现上述结果并不是唯一最优解。实际上，通过观察图5同样不难看出，在一定范围内调整各岸舰导弹作战单元的基准射向，仍然可以维持目标函数值不变，这就为指挥员根据阵地视界、射击扇面等实际情况进行决策提供了更大的决策空间。

在本算例中，A型岸舰导弹最大射击扇面角为±180°，理论上可以实现全向攻击，基准射向的变化不会引起目标函数值的改变，因此仅针对部署B型岸舰导弹作战单元的阵地4、阵地5进行讨论：在其他条件不变的前提下，以0.01π rad为变化单位，在[0 rad,π rad]区间内，观察目标函数值相对于阵地4、阵地5导弹射向的变化趋势，得到的三维曲面图如图7所示。

图7 目标函数值变化情况三维曲面图

分析结果表明：在区间[0.08π rad,0.58π rad]内调整阵地4导弹射向，在[0.4π rad,0.54π rad]内调整阵地5导弹射向，仍可实现目标舰船在各目标散布点毁伤值之和最大。此外需要说明的一点是：由于航路规划功能对岸舰导弹的最大有效射程有一定影响，且影响程度取决于航路点数量，涉及的情形较为复杂，因此本文结论的主要应用对象为不具备航路规划功能的岸舰导弹。

4 结论

本文针对多阵地岸舰导弹组合攻击作战任务中预设阵地选择与作战单元部署问题，构建了多型岸舰导弹作战单元部署优化模型，并针对模型特征设计了优化算法。得出以下主要结论：

1)本文算法可以稳定、精确地对多型岸舰导弹作战单元优化部署模型进行解算。

2)经过优化仿真得到了真实、合理的部署方案，表明本文模型可以为多型岸舰导弹作战单元部署的战时决策提供参考和依据。