考虑水泥土刚度的预制矩形桩在基坑工程的应用

陈 晨

（安徽理工大学土木建筑学院，安徽 淮南 232001）

1 矩形桩与水泥土相互作用原理

假设水泥土与矩形桩组合结构截面在荷载的作用下发生形变仍在同一个面内，不考虑水泥土与矩形桩之间的滑移，忽略材料的温度、收缩等因素对材料产生的不利影响且两种材料在外力的作用下变形具有相同的曲率，水泥土与矩形桩在荷载的作用下可分为以下四个阶段：

第一阶段：水泥土与矩形桩均为弹性；

第二阶段：受拉区水泥土发生开裂，矩形桩仍为弹性；

第三阶段：矩形桩单独工作阶段；

第四阶段：组合结构发生破坏。

当水泥土与矩形桩均处于第一阶段时，两者均处于弹性阶段，此时水泥土与矩形桩组合结构刚度可表示为：

式中B为组合刚度；Es，Eh为水泥土、矩形桩弹性模量；IS、Ih为水泥土、矩形桩截面惯性矩。

但实际工程中，水泥土与矩形桩均不可能处于理想的弹性状态，参考郑刚等人进行型钢与水泥土抗弯试验研究[1]，水泥土与矩形桩组合刚度可表示为：

式中Bini为考虑水泥土刚度贡献系数的组合刚度；α为水泥土刚度贡献系数。

2 工程实例研究

2.1 工程概况

本项目位于上海市，基坑开挖深度范围内分部的土层主要有素填土及局部分布的浜底淤泥、灰黄色黏土、淤泥质粘性土及砂质粉土。基坑下部分布有淤泥质黏土、软塑粘性土，土的基本物理力学参数见表1。场地地下水位埋深为0.5～0.7m。

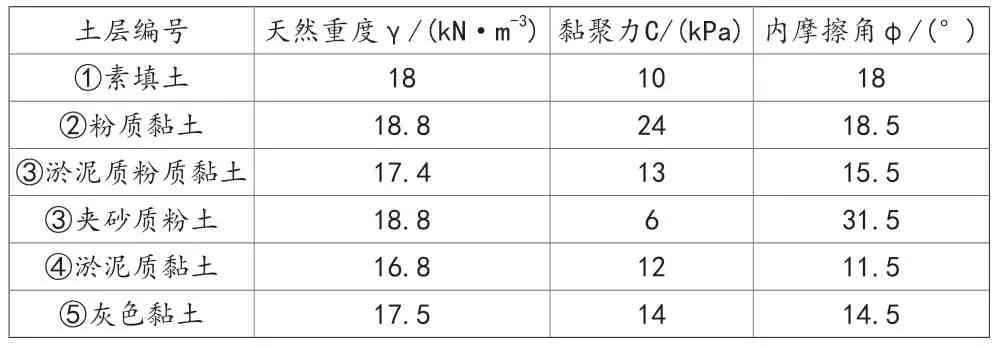
表1 土的物理力学参数

2.2 基坑支护的围护结构设计

本文选取项目基坑开挖深度约6.95米，基坑安全等级三级。竖向围护结构采用850mm厚水泥土墙内插650*300预制矩形桩，矩形桩间距600mm。水平内支撑采用一道型钢内支撑，围护结构设计采用启明星FRWS进行设计，对考虑水泥土强度及不考虑水泥土强度作用的情况分别进行计算。预制矩形桩采用C30混凝土，水泥土弹性模量取2000Mpa。计算时采用刚度等效的方法将矩形桩以及水泥土+矩形桩的组合结构等效成地下连续墙来计算。

仅考虑矩形桩刚度时，将矩形桩换算成单位长度的地下连续墙，假设地下连续墙厚度为h，弹性模量为Ec，根据刚度等效原则可得：

考虑水泥土刚度时，将水泥土与矩形桩组合截面换算成单位长度地下连续墙，假设地下连续墙厚度为h，弹性模量为Ec，根据刚度等效原则可得：

设计计算工况如下：

工况1：开挖至支撑标高以下0.5m；

工况2：架设型钢内支撑；

工况3：开挖至坑底；

工况4：底板换撑；

工况5：拆除型钢支撑。

经计算，两种情况围护结构变化规律基本一致，安装内支撑前，围护结构处于悬臂状态，最大位移在桩顶位置处，随着深度的增加逐渐减小。因此工况位移较小，水泥土的作用未完全发挥，考虑水泥土作用的矩形桩水平位移略小于仅考虑矩形桩刚度的情况。基坑开挖到底后，因为支撑的约束作用，无论是否考虑水泥土强度的影响，矩形桩桩顶位移均仅有少量增加。整个桩身位移呈两端小中间大的凸形，最大位移在坑底位置附近。此时考虑水泥土刚度的矩形桩计算得到的深层水平位移最大值为25.6mm，未考虑水泥土作用时，深层水平位移最大值为27.7mm，两者相比最大位移减少了约8%。

2.3 水泥土刚度贡献系数的确定

在实际工程中，如计算时未考虑水泥土作用时，得到的结果偏保守，深层水平位移偏大，不考虑水泥土刚度折减时，由于水泥土性质为非线性，当位移过大的情况下，会高估水泥土对矩形桩的刚度作用。根据王建[2]等人给出的水泥土刚度系数曲线分别计算系数时矩形桩的深层水平位移，与之对应的计算位移最大值分别为：27.2mm、26.6mm、26.2mm、25.9mm。由于基坑工程中围护桩最大水平位移对基坑及周边环境影响最大，因而通过考虑不同水泥土刚度作用的最大深层水平位移与现场监测值进行对比，得出大致的水泥土刚度贡献系数。随着基坑的开挖，桩身最大水平位移实测值为26.3mm。经过对比发现，当水泥土刚度贡献系数=0.7时，计算出的竖向围护最大深层水平最大值与监测值最接近。

3 结论

1）通过启明星FRWS计算发现，水泥土刚度提高了竖向围护结构的整体刚度，考虑水泥土刚度相较于只考虑矩形桩的情况，最大深层水平位移减小了8%。

2）通过对刚度贡献系数取不同值计算，与桩身深层水平位移监测值比较发现，当时，计算出的深层水平位移最大值与监测值最为相近。

3）竖向围护设计时，考虑基坑工程的复杂性，影响因素较多，不能做到计算值与实测值一致但仍可为今后类似相关工程设计提供参考。