基于接触式传感体的传感器接触应力分析与疲劳寿命计算

李薪宇， 孟丽君， 谭昕

（江汉大学 智能制造学院，武汉430056）

0 引言

信息科技快速发展，传感器技术应运而生，并且在各个领域扮演重要的角色[1-2]。传感器一般由传感体、转换原件、信号调理转换电路等3部分组成，其中传感体是直接感受或响应被测量的部分。很多传感器的传感体是通过点、线等高副接触实现力的传递和传感。如双光束传感结构中利用接触梁的形变测量位移[3]、斜锥齿轮可变测量精度位移传感器中，利用的齿轮接触面测量对应位移[4]等。但目前的研究大都集中在传感器的结构设计上，缺少对其关键部件尤其是点线接触的传感体的接触应力和寿命的分析。实际上，在传感器工作过程中，点、线的接触应力大，应力变化规律复杂，长期使用会造成传感体表面材料的剥落或裂纹，继而造成传感精度下降甚至失效[5]。

本文利用COMSOL、ANSYS Workbench等软件分析了一种基于悬臂梁接触式传感器传感体的接触应力及其影响因素，并开展了疲劳寿命的仿真分析，为基于接触型传感体的传感器疲劳分析问题的研究提供一种方法。

1 传感器结构原理

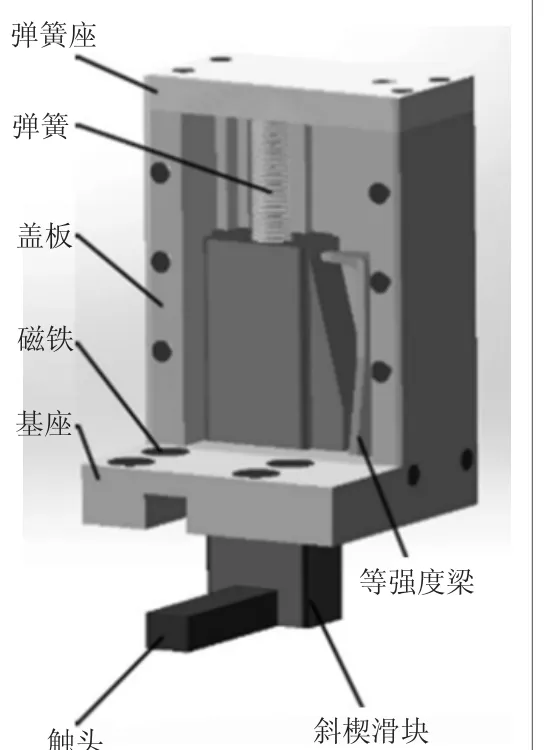
图1 传感器结构图

该传感器主要应用于白车身车门间隙测量当中。白车身是指将冲压件或者外来件及总成固定在工装夹具上，通过热连接或者冷连接技术将零件连接在一起并且未进入喷漆车间之前的车身框架。其最主要的尺寸误差来源于焊装工艺，而这些待测部位往往位于车身内部，不方便测量，为实现车身内间隙的在线设计，设计了一种基于等强度梁的光纤光栅传感器。如图1所示，传感器主要由悬臂梁、滑块、基座、触头、盖板、磁铁等部件构成。工作时，当触头产生位移时，会带动滑块产生相应的位移，并引起悬臂梁自由端产生挠度变化，从而促使贴于悬臂梁表面的光纤光栅产生波长变化，光纤光栅的波长变化量和其承受的应力成正比。通过对比不同位移量与对应的光纤光栅的波长变化量，进而获得触头的位移变化量，实现边界位移的测量[6]。

当悬臂梁和滑块互相压紧时，会在接触区域产生相应的应力和变形，称之为接触应力和接触变形[7]。由于传感器工作原理，其接触区域具有往复性，在较高的接触应力的反复作用下，会在接触表面的局部区域产生小块或小片金属剥落，并形成麻点与凹坑，使其零件振动加剧，磨损加快，从而影响传感器的测量精度。

本文利用COMSOL有限元分析软件建立接触应力计算模型，根据仿真模型研究了传感器的悬臂梁不同材料、不同悬臂梁端部弧度及不同接触线长度在形变过程中对悬臂梁的最大接触压力分布的影响状况，为传感器材料的选取和结构尺寸的确定提供依据。

2 有限元模型的建立

随着分析软件的不断优化，不同于过去依托传统的公式计算，现利用有限元软件进行分析是一种更加精准高效的方法。本文利用SoildWorks、COMSOL及ANSYS Workbench来进行建模及仿真分析。其中SoildWorks进行悬臂梁的三维建模，然后在COMSOL中进行材料的赋予、网格的划分及边界条件的限定， 并最后在ANSYS Workbench中进行疲劳寿命和破坏的分析。

根据光纤光栅间隙传感器的设计要求，设计了悬臂梁式光纤光栅位移传感器的传感结构接触模型。悬臂梁通过螺钉固定在基座上，触头位移时带动滑块产生相应的位移，从而引起悬臂梁的挠度变化，因触头、基座等零部件对悬臂梁的接触应力分析无关，故在分析中不对其进行模型的建立，其接触应力的模型如图2所示。

光纤光栅位移传感器工作方式为悬臂梁固定、滑块为输入控件。故边界条件为:悬臂梁为固定约束，限制滑块X、Y方向的自由度，指定Z方向上的位移。

COMOL中对于接触应力分析有两种不同方法[8]：一种为Augmented Lagrangian方法，另一种为Penalty方法。Penalty方法是基于惩罚因子的模型基础运算方法，与Augmented Lagrangian方法相比，这种方法可以加快计算的速度，并提供更加平滑的收敛。本文采用Penalty方法对检测部位进行有限元分析。

图2 接触应力的模型

3 接触应力有限元分析

3.1 不同材料下的接触应力分析

传感器悬臂梁是重要的传感元件，其应变效果是传感器准确测量的前提。故需对其材料进行合适的选择，以提高其传感敏感性，并且保证接触应力不至于过大。

光纤光栅传感器的滑块部件采用了ZCuAl03Sn09，该材料耐腐蚀能力强，抗氧化性能十分优秀，耐磨性好，能够满足悬臂梁在斜楔部位滑动要求。在此基础上分析悬臂梁材料不同时接触应力和表面应力的差异，悬臂梁的不同材料参数如表1所示。

悬臂梁材料为45 钢时，传感器滑块位移过程中，其接触压力变化曲线如图3所示，分析得知，在位移量3～5 mm之间，最大接触压力变化比较平稳，位移5～10 mm之间时，变化趋势近似呈线性。当到达最大位移10 mm时，最大接触压力到达319 MPa。

考虑到传感器实际测量范围，通过COMSOL有限元分析计算滑块位移9.975 mm的情况下的Von mises等效应力、最大接触压力、触头集中接触压力范围。悬臂梁材料为45钢时的分析结果如图4所示。悬臂梁的等效应力比较均匀，主要在80 MPa附近，而螺栓连接孔处的等效应力较大，最大可达到205 MPa 悬臂梁L形末端的等效应力较小，而L形末端圆弧触头处接触压力最大，最大接触压力可达313 MPa。且最大等效应力小于其屈服强度，满足设计要求。

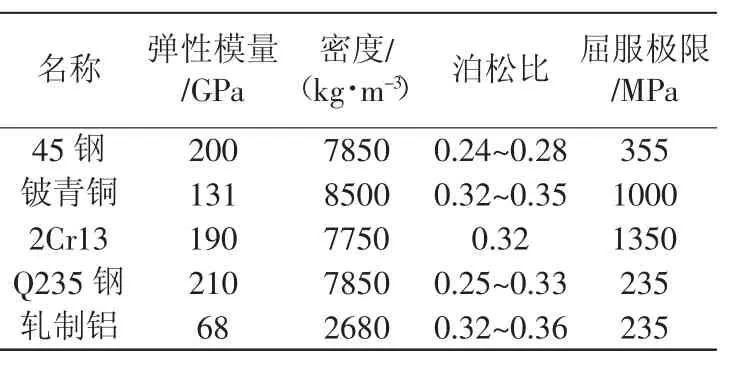
表1 悬臂梁不同材料物理参数

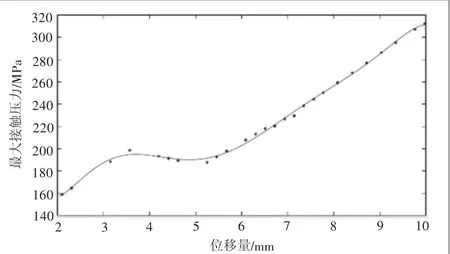
图3 位移-最大接触压力曲线

图4 45钢的分析结果

同样地，分析悬臂梁材料分别为2Cr13、Q235、轧制铝的结果，其结果如表2所示。

由分析结果可知，2Cr13、45钢皆满足等效应力要求，接触应力分布均匀，接触压力集中区域适中。但从耐腐蚀性、强度、韧性、抗氧化性、热强性及价格成本考虑，故在悬臂梁材料选用上选择45钢。

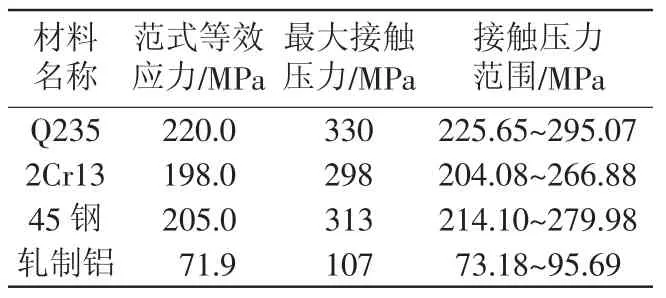
表2 悬臂梁不同材料下的分析结果

3.2 不同接触弧度下的接触应力分析

通过改变悬臂梁的触头区域直径大小，从而改变接触区域的弧度大小，通过COMSOL有限元分析计算滑块位移9.975 mm情况下，悬臂梁不同触头弧度半径下的范式等效应力、接触压力、触头集中接触压力范围。其结果如表3所示。

在其研究结果的基础上，当弧度直径在0.7 ～0.9 mm时，利用Matlab 对弧长和最大接触应力的关系进行了最小二乘法拟合，得到其弧度-最大接触应力的拟合曲线，其变化规律曲线如图5所示，发现随着接触头直径的增加，其最大接触应力逐渐减小，且当接触头直径在0.7～0.9 mm范围内，两者有近似线性关系，参考加工工艺、等效应力、接触应力大小，选择弧度直径为0.8 mm。

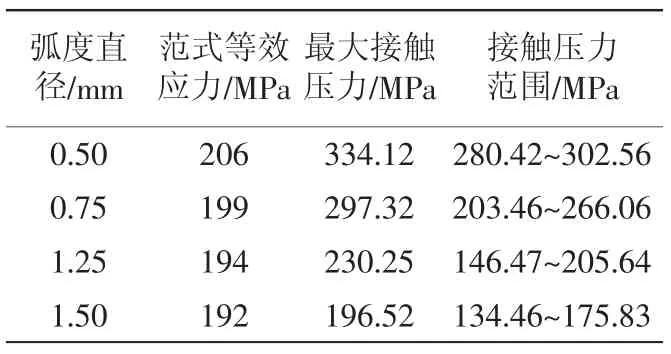
表3 不同弧度的分析结果

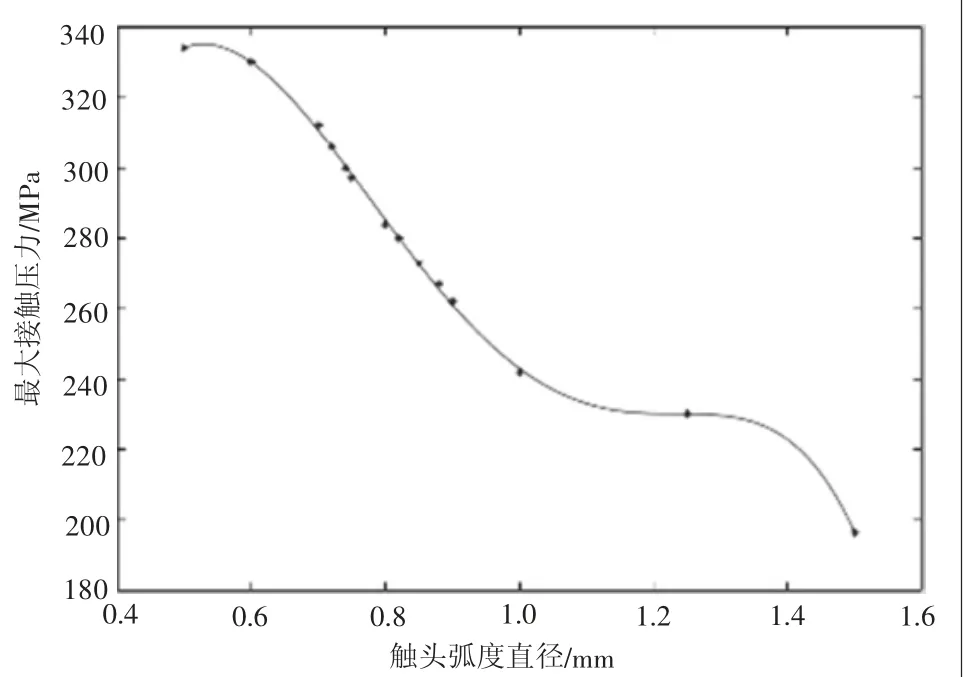
图5 弧度-最大接触应力对应关系

3.3 不同接触线长度下的接触应力分析

接触线长度即为接触头宽度，是悬臂梁与滑块直接接触区域。通过改变悬臂梁的接触线长度，通过COMSOL有限元分析计算滑块位移9.975 mm情况下，悬臂梁不同接触线长度下的范式等效应力、接触压力、触头集中接触压力范围。其结果如表4所示。

在分析的上述不同数据结果的基础上，接触线长度0.9～1.1 mm取10个采样点，对比不同采样点情况下的接触应力情况。在Matlab中使用最小二乘法进行数据预测，接触线长度-最大接触应力的拟合曲线与变化规律，其曲线图如图6所示。

表4 不同接触线长度的分析结果

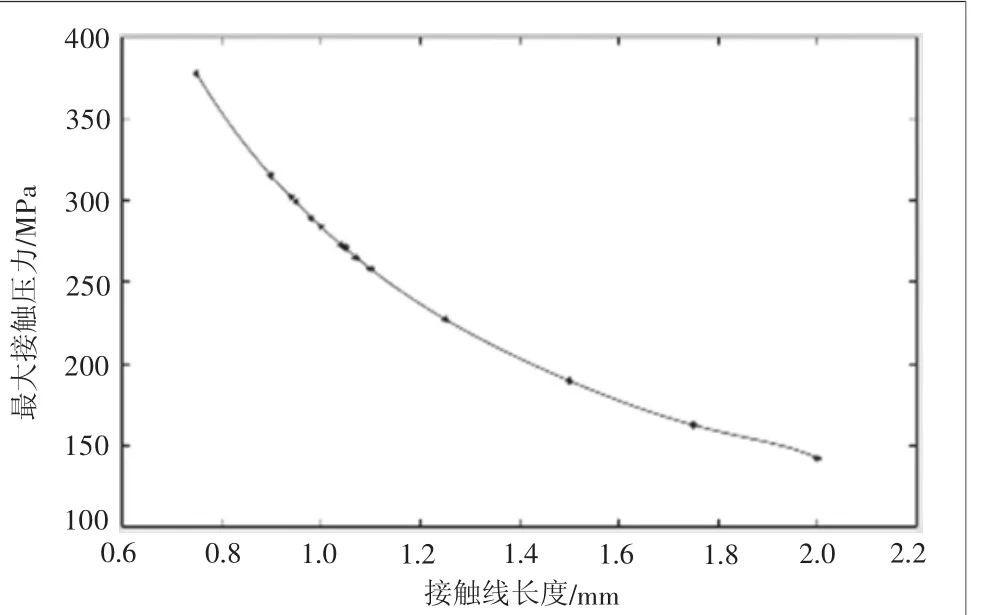
图6 接触线长度-最大接触应力对应关系

由接触应力产生原理可知，施加载荷后，两弹性物体的接触面的普遍形式为一椭圆。在改变接触线长度时，其接触面积也发生了对应的改变。对比取样段数据曲线发现，在一定范围内，接触线长度的增大，最大接触应力在逐渐减小。考虑加工工艺的限制、悬臂梁整体尺寸的限定、范式应力分布、触头表面集中接触压力范围，触头接触线长度取1 mm。

4 疲劳分析

传感器工作过程中，由于工作特性，悬臂梁长期处于受载情况，点、线的接触应力大，应力变化规律复杂，长期使用，会造成传感体表面材料的剥落或裂纹，继而造成传感精度下降甚至失效[9]。故需要了解研究零件的预期疲劳程度及破坏特性[10]。本文通过ANSYS Workbench的静力学分析模块对悬臂梁进行疲劳分析。

选用45钢作为悬臂梁材料，在悬臂梁疲劳寿命分析中，选择最极限的工况进行分析。根据弹簧弹力系数、滑块最大位移量、斜面斜率，在ANSYS软件中施加悬臂梁触头法向的载荷，其Y轴分量为8.73 N,Z轴分量为-2.18 N；同时限制悬臂梁X、Y、Z轴的移动，以及Y、Z轴的转动，其结果如图7所示。

图7 悬臂梁载荷及约束加载

通过有限元软件ANSYS Workbench 对悬臂梁进行静力学仿真求解，可以得到悬臂梁应力云图如图8所示。悬臂梁的触头区域和等强度区总体应力水平比较平稳，在连接区域应力水平较大，最大应力处于固定端正面上区域，该连接区域上端存在应力集中，其应力最大值为230.63 MPa，材料的屈服极限为355 MPa。因此静力学计算结果小于材料破坏的屈服极限，满足静强度要求。安装螺栓后连接螺栓孔的载荷会被分担，而悬臂梁梁身的载荷才是影响梁体发生破坏的主要因素，其应力主要分布在102～150 MPa范围内，远小于其强度极限要求，因此静载作用下，整个结构的强度满足要求。

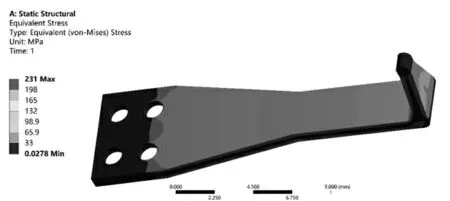
图8 悬臂梁应力云图

疲劳寿命的估算需要零件材料的S-N曲线，45钢的SN曲线如图9所示。根据传感器真实使用要求，将循环次数设置为106次，对应的材料S-N曲线中的疲劳极限数据为193.55 MPa。

在ANSYS Workbench的Fatigue Tool模块中设置疲劳分析选项并对模型进行求解，得到悬臂梁的等效交变应力云图和疲劳寿命云图如图10所示，悬臂梁的等效最大交变应力为184.5 MPa，小于材料S-N曲线中对应的疲劳极限，满足疲劳寿命要求。疲劳寿命云图如图11所示，其危险区域寿命为3.4462×105次循环，满足传感器实际使用需求。

图9 45钢S-N曲线

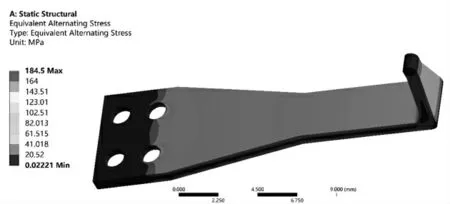
图10 等效交变应力云图

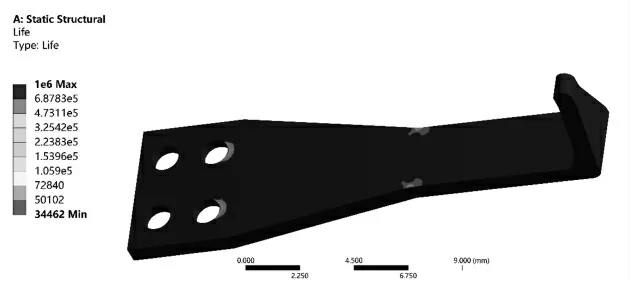
图11 悬臂梁疲劳寿命云图

5 结论

利用SoidWorks建立了一种接触性传感体的接触应力模型，在COMSOL有限元分析软件中，模拟不同传感器材料、接触弧度、接触线长度对接触应力和等效应力的影响规律。仿真发现，在Q235钢、45钢、2Cr13、轧制铝几种材料中，45钢具有良好的接触应力的表现状况，可作为传感体悬臂梁的优选材料。随着接触弧度、接触线长度的增加，接触应力逐渐减小，考虑加工工艺和接触强度的双重限制，可将传感器触头弧度控制在0.7～0.9 mm内，接触线长度控制在0.8～1.0 mm范围内。在此基础上，利用ANSYS Workbench软件研究了最大接触应力230.63 MPa作用下，传感体关键部件悬臂梁危险区域的疲劳寿命3.4462×105次循环。这些研究内容的开展，对分析精密传感器的接触应力和使用寿命提供了理论依据。