一种基于混沌系统的分段式图像加密算法*
乔建平 , 关来德
(柳州职业技术学院,广西 柳州 545006)
混沌系统具有初值敏感性、遍历性、参数可控性以及伪随机性等特征,因而,基于混沌的图像加密算法成为研究热点。笔者设计了一种新的分段加密方案,运用二维正弦逻辑调制映射(two-dimensional Sine Logistic Modulation Map,2D-SLMM)产生的密钥,对像素移位置乱,再对置乱图像进行分段灰度值替代操作,仿真分析验证表明,该加密方案在各加密参数方面达到要求。
1 混沌系统
2D-SLMM系统其数学表达式[1]为:
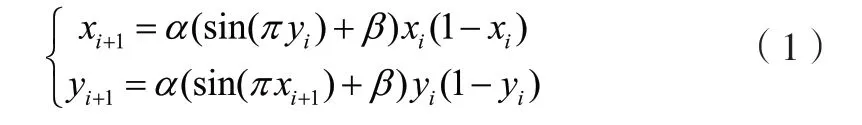
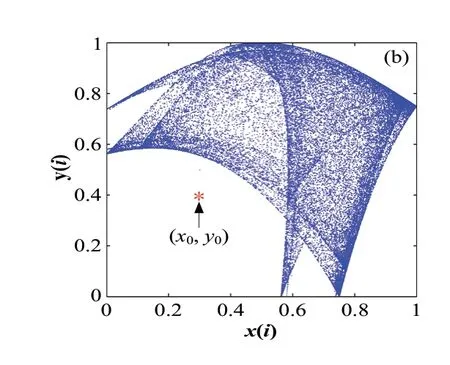
图1 2D-SLMM系统的分岔图
其中α和β为系统控制参数,α∈[0,1]和β∈[0,3],当α=1、β=3时,轨迹分布如图1所示,可看出系统具有极为复杂的混沌离散特性。
2 算法设计
2.1 移位置乱过程
假设原始图像为P,长宽为L=M×N,利用公式(1)和(2)得到指数系数a。
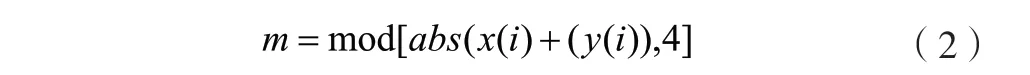
依据表1中a取值,通过公式(3)生成矩阵序列K,有M行、N列,其中x(i)和y(i)为2D-SLMM的迭代状态值,舍弃前500次迭代值,以防暂态效应,S为P所有像素值之和,floor(x)表示取不大于x的最大整数。
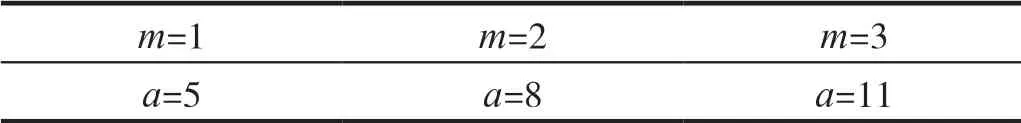
表1 指数a取值
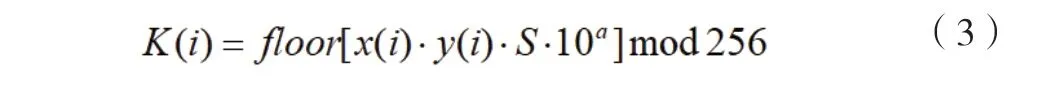
假设矩阵K中的每一行序列为R1,R2,R3,R4,R5,…,RN-1,RN;重新排列得到新的序列;例如,对第一行序列R1={r1,r2,r3,…,rN-1,rN}按升序由小到大排序,得到新的有序序列,同时生成用于记录序列中各个元素在原序列R1中位置的新序列S1={s1,s2,s3,…,sn-1,sn}。同理,以同样的方式重新排列序列R2,R3,R4,R5,…,RN-1,RN;得到S2,S3,S4,S5,…,SN-1,SN;由新序列组成排列矩阵S,分别用序列S1,S2,S3,S4,S5,…,SN-1;SN置乱原始图像P的每一行的像素值。
同理,对矩阵K的列排序得到排列矩阵T,使用类似行置乱方式对矩阵P进行列置乱,得到置乱图像C,置乱示意图如图2所示。

图2 置乱过程示意图
2.2 灰度值加密过程
为提高加密算法的安全性,须对置乱图像进行灰度值替代加密,对置乱像素进行分段式灰度值替代操作,算法如下:

经过上述步骤分段式加密得到加密图像,解密是加密的逆过程。
3 实验结果与分析
实验模拟仿真阶段选取大小为256×256(M×N)的Baboon标准图像进行测试,2D-SLMM系统参数α=1 和β=3,以及设定初始值。图3(a)为原始图像,加密和解密图像分别如图3(b)、图3(c),加密图像无原始图像的任何有效信息,解密图像与原始图像相同,说明本文算法有充分的可行性。

图3 加密流程图
3.1 直方图特性分析
直方图方可直接反映其质量特征的分布情形,图4为原文标准图Lean的直方图和加密图像直方图,前后两者的直方图有很大的区别,后者各个灰度级直方图分布均等,可以抵挡结合灰度级数值统计的攻击。

图4 原始图像和加密图像直方图
3.2 信息熵分析
信息熵变大,从密文图像中窃取统计数值信息的难度越大。信息熵[2]数学表达式为:
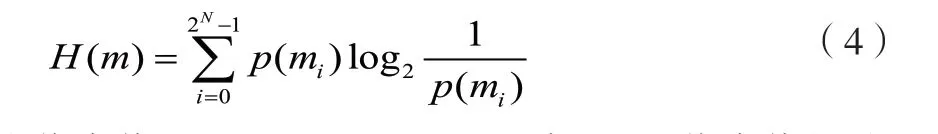
其中mi为像素值,p(mi)是mi出现的概率,N是像素值得总值,对于具有256个灰度级的图像,其信息熵的理想值是H(mi)=8。选取若干256×256 标准图,用公式(4)计算信息熵值,如表2所示,各标准图加密熵值都趋近8,说明本算法可抵抗熵攻击。

表2 不同图像的信息熵
3.3 抗差分攻击能力分析
像素数目变化率(NPCR)以及归一化平均变化强度(UACI)计算公式[3]为:
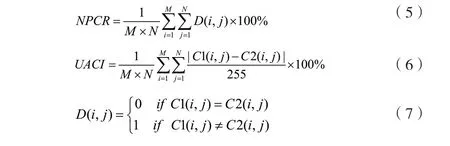
其中C1是原图密文,C2是变化后的密文,两者的原始图像素点仅仅差别一个值;C1(i, j)和C2(i, j)分别代表两个密文在(i, j)点的灰度值,C1(i, j)=C2(i, j)时,D(i, j)=0,C1(i, j)≠C2(i, j)时,D(i, j)=1,对若干标准图像统计得到50组的NPCR和UACI,其平均值在列表3中,加密图像素数目变化率以及归一化平均变化强度均值均趋近其相最佳理论值,反映加密方案抗击差分攻击性的能力好。

表3 加密图像NPCR和UACI的平均值
3.4 相邻像素相关性分析
分别在对角线、垂直线和水平线三个方向随机选取5000个相邻像素对进行抽样检测。加密前邻近像素点在靠近y = x函数区域集中,如图5所示,加密图像邻近像素点在整个坐标区域内分布均匀,该方案有能力解决像素邻近点处相关性强的问题。
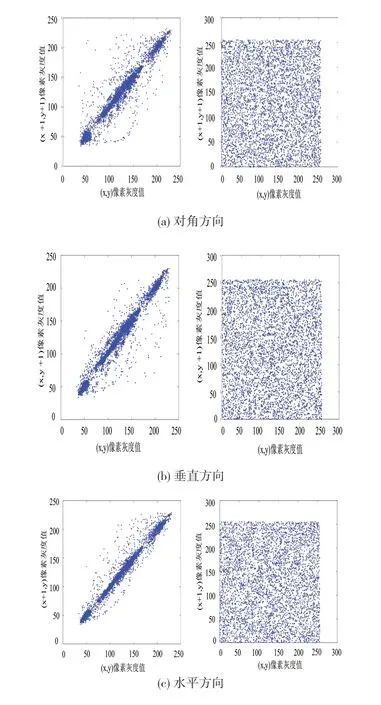
图5 原文和密文图像相邻像素间的相关性图
3.5 加密时间分析
仿真试验阶段,在MATLAB R2018a平台上来运行图像加密程序,计算机采用 Microsoft Windows 10操作系统,实验硬件环境设备为2.4 GHz Intel(R) Core(TM) i3 CPU,2.0 RAM和300 G 硬盘的手提式电脑。表4罗列出了本章加密方案和其他加密方案对256×256的标准图的加密效率的数据对比,充分显示了该方案在加密速度上有明显优势。

表4 本章算法与其他算法加密效率比较
4 结论
通过对2D-SLMM定义和混沌特性进行简要分析,提出一种基于混沌系统的分段式图像加密算法,实现了数字图像像素位置快速移位置乱,并进行分段式灰度值扩散操作,最后完成了图像加密。实验分析表明,该方案加密效率高,安全性高。

