不完全修复下PET/CT设备故障分析
刘龙,陈颖,储呈晨,孙雨骐,杨海
1.上海交通大学 生物医学工程学院,上海 200030;2.上海交通大学附属第六人民医院 a.医学装备处;b.医院管理研究中心;c.人事处,上海 200233;3.复旦大学 公共卫生学院,上海 200032
引言
国家卫生健康委员会将X线正电子发射断层扫描仪(PET/CT)配置许可管理由甲类调整为乙类,作为大型医用设备,国内PET/CT市场随着配置开放将迎来快速增长的发展趋势。根据财政部、卫生部制定的《医院财务制度》[1],PET/CT的折旧年限为6年,而配置一台PET/CT需要投入2000~4000万元[2-3],容易给医院带来经济亏损。为确保设备投入后为医院带来可靠的经济效益和社会效益,必须加强PET/CT设备的运营管理[2]。医疗设备的可靠性分析包括设备的故障分析,通过分析设备故障变化趋势,建立可靠性模型,从而制定最优化的设备管理策略,可以有效提高设备使用效益。
描述可靠性的重要参数有可靠度、平均寿命(不可修复系统)、平均故障间隔时间(可修复系统)、故障率等,目前,对于设备可靠性已有较多研究[4-7]。对于可修复系统的可靠性研究,首次故障时间、平均故障间隔时间、平均修复时间、可用度受到重要关注。对医疗机构的PET/CT设备管理而言,唯一的首次故障时间无法提供更多关于设备的可靠性信息,设备故障后故障特性的变化仍需有效手段进行评估,以便及时采取相应的维护措施。
对设备故障时间进行分布检验,是常用的故障特性分析手段,常用的数学模型有Weibull分布[8]、指数分布[9]等。因PET/CT设备是可修复型设备,对其故障间隔时间直接进行分布检验,需满足连续的故障间隔时间之间独立且同分布的条件[10]。换言之,设备在修复后,性能“修复如新”,这是一种理想状态。现实中,当PET/CT某部件发生故障时,通常对其尽可能修复或直接替换新部件,此时PET/CT功能恢复,但除故障部件,其余部件并未得到修复,这些部件的工龄要大于被修复的部件,故设备性能不可能与新安装时等同。因此,不完全修复更符合PET/CT设备的现实情况。基于上述分析,本文对某三甲医院的某型号PET/CT设备开展故障特性分析。
1 故障间隔时间趋势检验
为研究PET/CT设备故障特性,本研究收集了北京市某三甲医院的某型号PET/CT设备从安装使用至2018年12月31日期间的维修记录。设备在此期间共发生35次故障、5次维护保养,见表1。设备在安装后3个年段内分别发生11、13、8次维修,如果忽略设备待机、保养、修复时间(远小于设备运行时间),该PET/CT设备的工作历程如图1。

表1 本台PET-CT故障间隔时间和保养时间(h)

图1 PET/CT设备工作历程
设备从时间t=0开始运行,xn表示从第(n-1)次修复后到第n次故障发生时刻的设备工作时间,x1,x2,…xn为相邻故障间隔时间。第n次故障发生时,设备已工作时间为Tn=∑ni=0xi。对x1,x2,…xn进行独立同分布检验或样本趋势分析,见公式(1)[11]。

未考虑保养措施下,若直接将连续故障间隔时间序列x1,x2,…xn按数值从小到大进行排列,利用K-S检验,可以发现样本服从Weibull分布(P=0.7672)和指数分布(P=0.1791),这可能会导致错误的结论。
图2展示了直接对设备故障间隔时间进行Weibull拟合、指数拟合的结果,且拟合效果较好。从指数分布橙色曲线可以看出,大约在667 h以内的运行时间中,PET/CT的存活曲线一直高于拟合曲线,在1200~2200 h内一直低于拟合曲线。这可能表明设备在短期内运行的故障率具有较大概率低于估计值,而长期运行下故障率要大概率高于估计值,即设备故障率存在变化趋势。

图2 PET/CT故障间隔时间分布拟合
2 不完全修复模型
考虑在维修的影响下设备故障率的变化[12-14],当设备在维修后达到“修复如新”,即“完美修复”时,故障率返回新设备状态,故障分析可以直接按不可修复设备进行,设备故障率满足“更新过程”;如果设备修复后故障率恢复到本次故障发生前,即“最小修复”,系统故障率在维修前后不发生变化,设备故障模型可以用非齐次泊松过程表示;若设备修复后性能处于“完美修复”和“最小修复”之间,故障率随机处于上次故障之前某个时刻,则用“不完全修复”模型表示故障率变化规律。
设{ti}i≥1为故障发生时间序列,设备从t0=0时运行。Nt为t时刻累积已发生故障次数,设备故障发生后产生的修复时间忽略不计。为建立不完全修复模型,Kijima[14]提出虚龄概念At,建立了算术降龄(Arithmetic Reduction of Age,ARA)模型。该模型假设:设备未发生故障条件下,设备工龄为t的函数,可简单认为At=t,设备在t时刻的故障率λt=λ(t)。当设备发生维修或保养后,可以认为设备因得到“更新”而变得“年轻”,其工龄要小于现实工龄,则t时刻的设备故障率与At时刻相等,且At ARA模型认为设备修复后的状态受到之前所有故障维修的影响,这导致故障率模型过于复杂,难以解析。Malik[16]将ARA模型进行简化,认为设备修复后的状态仅与上一次维修有关,得到ARA1模型。Doyen[15]将Kijima[14]和Malik[16]的ARA模型总结为ARAm模型,ARAꝏ和ARA1为ARAm模型的特殊情况。 不完全修复以ρ描述,可理解为维修效率[17-18]。ARA1模型中,设备在ti时刻发生第i次故障并立刻得到修复,其工龄一定概率上被减小,但只使得设备“读档”回到第(i-1)次故障修复后到本次故障之前的某个时间点。此时,设备虚龄满足公式(3)。当ρ=1时,则认为设备每次都得到“完美修复”,当ρ=0时,设备得到“最小修复”,0<ρ<1则意味着设备为不完全修复,t时刻设备故障率为λt=λ(t-ρtNt)。 然而,该模型仅适用于故障率增长的情况,对于初始故障率不断下降的情况,该模型会得出设备维修是有害的结论,因为设备维修降龄后故障率反而升高[19-20]。Dijoux[19]因此提出了适用于故障率非增情况下的不完全修复模型,对符合浴盆曲线的设备故障率变化进行了较好拟合,见公式(4)。 Dijoux模型假设设备早期故障率不断下降,即磨合期;在tin时刻开始处于常数,即平稳期;最后在tout时刻开始进入损耗期,故障率增长。在磨合期,设备保养、维修不会改变工龄,故障率与故障发生前一时刻相同,设备故障率变化符合非齐次泊松过程。平稳期和损耗期下,设备保养、维修服从ARA1模型。若设备某次故障间隔跨过tin,该次维修或保养后设备工龄仅返回到ti后某个时刻,以保证保养或维修的有益性。平稳期保养、维修不改变设备故障率,但降低工龄可以延长平稳期,最大化利用设备,提高效益。通常情况下,设备工龄或生命周期仅由工作时间表征,一些设备则由工作量如汽车的行驶里程表征,又或两者兼用[21]。当设备超负荷工作时,其工龄将以更快速度增加,但对于单台PET/CT而言,工作量对工龄的影响实际上已在λt与t的关系中体现了,只是无法识别出工作量、工作时间分别对工龄的作用,因此本文并不特地考虑工作量的影响。 从图2b可以看出,设备故障率存在下降过程。本文假设PET/CT故障服从浴盆曲线,早期故障率变化为幂律函数形式,且因所观测设备仅服役3年,可以认为设备正处于平稳期,建立故障率模型如公式(5)所示。 其中λ,α≥0,β>1。由于t>tin后设备故障率为常数,λ(t-ρ(tNt--tin))=λ,这使得Dijoux模型适用于未进入磨损期的设备。特别地,该模型隐含假设设备维修效率为常数的情况,而实践中往往并非如此[22],但由于设备正处于平稳期,对模型预测结果并不会造成影响。 为使得模型适用于本台PET/CT,需要对模型参数进行估计,常采用极大似然估计,考虑虚龄的似然函数表达式如公式(6)[8]所示。 因求解公式(6)过于复杂,Dijoux[19]提出了一种简便可行的参数估计方法。 首先假定曲线拐点tin∈(tk-1,tk),由此可以认为故障t1,…,tk-1发生在磨合期,tk,…,tn发生在平稳期,则。得到后,只需对磨合期的参数ɑ、β进行估计。磨合期服从非齐次泊松过程,设备累积故障强度函数如公式(7)所示。 本台PET/CT第一次故障前为非齐次泊松过程,其首次故障前平均时间(Mean Time To First Failure,MTTFF):,约为17 d。新设备在安装后随着运行时长增加,故障率在逐渐降低,故障间隔时间逐渐增大,大约经过4个月后到平稳期,设备故障间隔时间近似为653 h,约27 d,预示设备下一次故障可能发生的时间。在不完全修复模型下,该PET/CT运行3年累积故障强度变化如图3所示。 图3 PET-CT运行3年的累积故障强度变化 本文对某台PET/CT进行了故障分析,对连续的故障间隔时间进行趋势分析,发现故障间隔时间之间存在趋势变化,而非独立同分布。同时,这也说明了设备在故障发生后并未得到完全修复,因而本文选用了不完全修复模型对本台PET/CT进行分析。本研究在设备故障率服从浴盆曲线,且设备未进入磨损期的假设下,对设备累积故障强度趋势得到较好的拟合结果,设备早期的故障间隔时间为408 h,大约4个月后逐渐提高到平稳期的653 h,由此可根据设备状态制定相应的保养措施。 本研究采用的模型基于不完全修复理论和浴盆曲线假设,设备在磨合期为最小维修,服从非齐次泊松过程,平稳期及磨损期为不完全修复。然而,若所观测设备正处于平稳期,此模型则无法估算维修效率,即不完全修复程度。同时,在模型参数估计过程中,本文采用了较为简单的方法计算平稳期的故障率,对于单台设备而言,在小样本数据下容易出现偏差,只有在样本数量足够大时,估计量才接近真实值[19]。 对保养和维修过程的处理会影响模型分析结果,本研究假设磨合期的保养不改变设备故障率,若设备故障率有下降趋势,保养应在一定程度上降低设备故障率,且降低设备工龄。在工龄变化模型中,本研究将保养和维修对设备工龄的改变视为同等效果,且模型认为每一次的降龄效果是某个固定的常数,但对于此假设还需进一步分析。此外,本研究在拟合设备累积故障强度中,并未区分保养和维修,必然会对拟合效果造成干扰(图3显示第1次和第4次保养后曲线有波动现象),还需进一步对保养与累积故障强度的关系进行分析。 PET/CT设备为复杂多部件构成的大型医疗影像设备,理论上设备故障率在各部件相互作用下符合浴盆曲线。这种假设下认为各部件对整机的影响是相等的,因为设备在平稳期故障率是常数,任何一个部件出现故障后,不论是否为核心部件,即使引入了工龄概念,本研究模型仍认为设备故障率为常数。当设备某核心部件如球管发生故障后,若发生更换,其对整机故障率的影响应显著高于其他非核心部件。虽然该模型可证明设备得到维修和保养后工龄降低,可以延长浴盆曲线的平稳期,以此提高设备使用效益,但也说明其难适用于故障率在平稳期波动的情况。

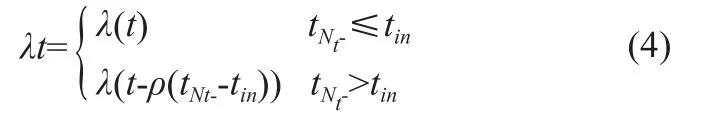

3 模型的数值求解
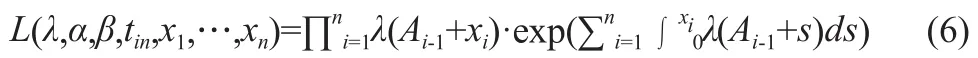
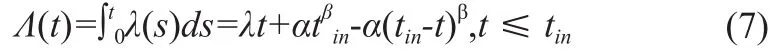
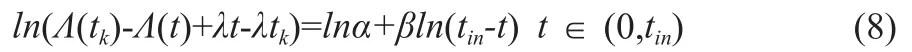


4 PET/CT设备故障趋势分析

5 讨论

