有压输水管道中气泡起动临界流速研究进展

杨诚志，王玲花，胡建永

(1.华北水利水电大学 电力学院，河南 郑州 450045，2.浙江水利水电学院 水利与海洋工程研究所，浙江 杭州 310018)

自古以来，因水资源分布不均，主要体现在空间分布东多西少，时间分布春夏多、秋冬少。为了解决水资源的相关问题，近年来我国建设了云南省滇中引水工程、广州市西江引水工程、延安黄河引水工程等。尽管在输水系统设计时，已经充分考虑到管道系统的排气问题，但由于运行工况十分复杂，长输水管道中会出现气泡聚集、气团滞留的现象。管道中的滞留气泡对管线有很大的危害，滞留在管线中的气泡会使管线的过水面积明显降低，增加了线路沿程损失，降低了系统的输水能力；同时，滞气留在管线中起动和排出时会使压力产生剧烈的波动，从而导致水锤的产生，可能会引起严重的事故[1]。长管道有压输水工程输水规模大、供水区域广，对输水安全性要求极高，需要高度重视有压管道滞气带来的安全隐患。因此研究有压输水管道的气泡起动临界速度，对输水工程的安全经济运行有重要意义。

1 输水管道中气泡起动临界流速理论研究

国内外学者对不同管段有压管道气泡起动临界流速进行了大量的研究，结果表明，其起动临界流速值是一个函数，它受多方面的因素影响，如表面张力、弗雷德数、管道的坡度等；气泡起动临界流速与重力加速度、管道直径的开方成正比。即：管道中气泡启动临界条件可用临界弗雷德数Frc=Vc/(gD)1/2表示(g为重力加速度，D为有压管路直径)，当管径增大时，相应的气泡起动临界流速就会增大[2]。本节将针对垂直、倾斜和水平三种不同类型的管段对气泡起动流速进行总结。

对于垂直管段，KOBUS[3]表明在有压输水管道中，垂直管段的气泡起动临界流速主要取决于浮力的方向和水流方向：在垂直向上管段，气泡受到的浮力方向和水流方向一致，管线输送气泡的能力最大；在垂直向下管段，气泡受到的浮力方向和水流方向相反，管线输送气泡的能力最小，如果管道流速较小，管中气泡将在管道顶部聚集形成气团。SALIH[4]对气泡在垂直管段进行了研究，得出了垂直向下管段气泡的流动速度和水流速度存在差值，称为气泡和水流的滑移速度，并取得了速度滑移率的数据。ZUKOSKI[5]通过实验得出结论：在垂直向下管段，管中气泡的起动流速与(g(D/2))1/2成正比，其中g是局部重力加速度，D是管直径。DAVIES. R. M[6]通过实验研究得出了垂直管段气泡起动流速对应的弗雷德数是0.33。

对于水平管段，一些学者认为气泡的起动流速在理想情况下应为零，因为浮力不作用于水流方向。但在实际工程中，气泡在管壁上附着时受到管壁的摩擦阻力等影响，仍然存在大于零的起动流速。BENDIKSEN[7]在0.02～0.05 m范围内测试小直径管道，结果表明水平流情况下确实存在漂移速度，并且实际上可能超过垂直流情况下的值。BENJAMIN[8]对这种情况进行了理论分析，认为气泡起动流速对应的弗雷德数是0.542。

对于倾斜管段，WISNER等[9]对100～244 mm的有压管道进行了气泡起动临界流速的实验和理论分析，得出了气泡起动流速对应的弗雷德数与不同管段角度的关系。KENT[10]针对不同管线坡度、相同管径的有压输水管线进行了气泡起动临界流速的研究计算，得出在相同管径下不同管道角度与起动临界流速的关系式，并且引出管中气泡无刚量数n与气泡体积及管径的比例关系，当n>0.8时，气泡起动临界流速与气泡体积无关。A.R.I是一家阀门制造商，为用户编制了一个在管道系统中调整和放置空气阀的程序，该公司提出了新的气泡起动临界流速对应的弗雷德数与不同管段角度的关系。CORCOS[11]对一条小管路直径的水平有压输水管线进行了相关研究，计算出该管线的弗雷德数为0.484。郭永鑫[12]建立了气泡起动临界流速模型，模拟了原型中气泡相应的比例关系，对气泡运动机理进行了分析研究，发现气泡极大地影响着管线的正常运行，该管线其弗雷德数约为0.22。

以上学者均将气泡起动流速和管径、管道倾角及重力加速度联系起来，但忽略了气泡体积、表面张力等参数对气泡起动临界流速的影响。经分析，研究气泡起动流速的学者大多针对n>0.8的气泡，该尺度适用于会出现大型气团的较小管径的工程中，如城市供水工程。在实际的大型供水工程中，管道中往往会出现较小的气泡，即气泡无刚量数n<0.8的情况，这种尺度下的气泡，不可忽略表面张力等微小的作用力，需进行气泡动力学分析。

倪冰[13]对气泡附着在固壁上的过程进行了分析，认为附着在固壁上的气泡形状是球缺或球冠，在水平静止表面上气泡只受表面张力和浮力的作用。朱炎[14]对水平管管壁吸附的气泡进行了受力分析，认为气泡受到浮力、管壁支持力、管壁摩擦阻力和水的拖曳力的作用，并得出了气泡受力平衡的公式。杨明[15]认为在垂直管段，气泡主要受浮力、拖曳力和表面张力的影响，当气泡受到向上的浮力和拖曳力大于向下的表面张力时，气泡起动；在水平管段，气泡受到的拖曳力大于摩擦阻力和表面张力时气泡起动。魏桥栋[16]对垂直管壁上的气泡进行了详细的受力分析，认为气泡在垂直方向受到的拖曳力和浮力、表面张力的分量达到了平衡，在水平方向气体动量力和表面张力水平分量达到了平衡，并且通过理论分析得出了气泡处的水流速度公式和拖曳力公式。许玲丽[17]对气泡在液体中的运动特性进行了分析，并对拖曳力的系数进行了讨论。管鹏[18]对附着在壁面的气泡进行了受力分析，得出了表面张力水平分量和竖直分量的计算公式。谢建[19]对不同雷诺数下的拖曳力系数进行了总结，得出了管中气泡受到的拖曳力的系数。

根据以上学者的气泡动力学分析，结合有压输水管道中气泡实际情况，得到有压输水管道管壁附着气泡受力模型(见图1)。其中，FS为表面张力，FB为浮力，FN为支持力，FSY表面张力的竖直分量，Ff为摩擦阻力，FD为拖曳力，FSZ为表面张力的水平分量。通过本模型可进一步研究气泡体积和表面张力等因素对气泡起动临界流速的影响。

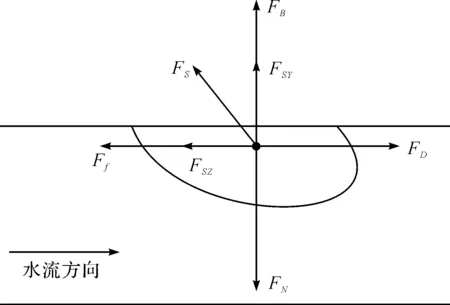
图1 有压输水管道管壁附着气泡受力模型

2 输水管道中气泡起动临界流速数值模拟研究

气泡运动规律的数值模拟方法当前主要有以下几种：①运用界面追踪的方式进行研究，如ALE模型、MAC模型等；②运用界面捕捉的方法进行研究，如运用level set、VOF和CLSVOF模型等。

对于界面追踪方法中出现的问题，HUGHES等[20]建立了ALE模型来解决流体力学中无法解决的问题，以此来对流体力学进行描述，并通过运用有限元法解决了自由表面的流动、不可压缩流体等问题。FUJITA[21]运用ALE建模，模拟了在各种浸润角黏附的变量条件下，水体单个气泡在起动前的体积变化过程。HARLOW[22]将连续的流场概化成了以拉格朗日离散点为基础的质点体系，并以此为基础创建了PIC模型(particle in cell)。RAHIM JAFARI[23]在ALE模型中加入了自己的代码，模拟了气泡在水中运动的过程，得出了气泡的增长率以及气泡与管壁之间的液膜形态。YING WANG[24]利用ALE模型进行了水下爆炸的数值模拟，总结了气泡的运动和破碎等因素对水下爆炸的影响。ThOMAS FOUREST[25]基于气泡动力学对ALE模型的keller-miksis模块进行了修改，得出的模拟结果与物理试验模型结果相吻合。HARLOW[26]为了提高模型界面的精度，以达到准确追踪界面变化的目的，对数值模拟进行了研究，他们在模型中引入只有坐标的虚拟标记点，将相界面改为带有记号粒子区域和没有带有记号粒子区域的交界面，并将这种模型命名为MAC模型，MAC模型因其准确性极高，可以处理间断的无数值耗散，但算法非常复杂，尤其是由低维度拓展到高维度时运用相对困难。

对于界面捕捉方法中存在的问题，OSHER[27]提出以等值面函数的点的集合为界面，并以等界面函数法命名，称为level set模型，这种模型只需等值面函数的值即可以自动计算界面的拓扑。叶再春[28]通过等界面函数，利用MATLAB平台对两个气泡的聚合过程进行了数值模拟，并成功的拓展到三维空间。张一夫[29]以不同雷诺数为变量条件，针对不同流场进行了数值模拟，通过贴体坐标系下的SIMPLE算法改进了level set模型，将流体的压力和速度矢量进行了耦合，模拟除了水体中气泡的形态变化过程及运动规律。HIRT[30]创立了新的流场数值计算VOF模型，通过模型应用了流体补偿的思想和迎风效应，这种运用donor-acceptor体系的模型应用开创了一个先河。范家瑞[31]运用VOF模型进行了有压管道的水气两相流的数值模拟，得到了水相体积分数等参数，并通过物理模型试验验证了数值模拟计算结果的可靠性。LORSTAD[32]以高雷诺数为条件基础，运用VOF模型进行了流体中气泡的数值模拟，并加入了表面张力模型。TING LIU[33]为了计算管线中气泡的起动临界流速，运用VOF模型进行了数值模拟，并耦合了k-ε湍流模型，计算了相同管径、不同坡度的有压输水管路的气泡起动临界流速。TONG LI[34]利用VOF模型，针对吉尔莫尔模型对球形气泡进行了验证，对非球形气泡进行了数值模拟，详细描述了气泡内和气泡周围的压力和速度场。张欣雨等[35]学者运用VOF模型对不同倾角的有压输水管线进行了气泡起动临界流速的数值模拟，并得出了不同倾角的气泡起动流速的相关结论。王祺来等[36-37]对不同倾角和管径的条件下弯管线应用VOF模型进行了气泡起动临界流速的数值模拟，结果显示，在速度相同的情况下小倾角、小管径的管线更容易将气泡排出。

耦合模型是气泡起动临界流速数值模拟研究的趋势，BOURLIOUX等[38]人对气液两相流模型进行了大量的研究，他们利用VOF模型和level set模型的优点，将二者进行了有机结合，耦合出CLSVOF模型，该模型需要计算VOF模型的体积函数、level set模型的距离函数，其兼具两种模型的优点，更加适用于气液两相流的数值模拟。孙东亮[39-40]同样耦合出了一种新的计算气液两相流的模型，将它命名为VOSET模型，该模型同样是对VOF模型及level set模型的耦合，在提高了相界面的准确度的同时保证了质量守恒，同时兼顾了VOF模型及level set模型的优点。宋云超[41]对CLSVOF模型进行了验证，他用该模型对有压输水管道中的气液两相流进行模拟，并与VOF模型进行了比较，计算结果证明采用CLSVOF模型对气液两相流的计算结果更加准确；相比于VOF模型，虚假速度问题也得到了明显的改善，更适用于气泡的起动临界速度研究。Z SHANG[42]通过CLSVOF模型模拟了气泡上升的过程，得出了相关的结论，并在垂直管中进行气液两相流的数值模拟，得到了比VOF模型更加准确的数据。ANDREA FERRARI[43]在levelset模型和VOF模型的基础上提出了flexCLV耦合模型，该模型兼具VOF模型在质量守恒方面的优势和levelset模型在表面张力精度方面的优势，并通过物理模型试验进行验证，flexCLV模型能更好的处理气泡在有压输水管道中的运动问题。

3 输水管道中气泡起动临界流速物理模型研究

在研究有压输水管道中的气泡的运动过程、形态变化等问题时，需要理论研究和数值模拟进行量化分析，但更需要物理试验对研究进行支撑，相比理论分析和数值模拟，物理试验研究更加直观，因此物理试验在气泡的起动临界流速研究中仍然处于主导地位。当前研究有压输水管道中气液两相流的观测方法众多，可概括为图像法、激光多普勒技术和粒子图像技术等。

图像法是一种较为常用的方法，通过运用高速相机等最新的图像获取技术得到有效的流场中的气泡运动图像，再通过相关软件进行处理，可以得到流速、压力等相关参数。运用图像法不会对流场进行干扰，同时也获取了相关的数据，试验操作过程也相对简单[44]。李庆浩[45]利用光场相机，建立了一种新的测量流场中气泡运动形态的方法，并且该方法实现了三维运动轨迹的模拟，结合软件处理获得气泡的深度信息，如气泡的形态、在流场中的分布等参数。罗涛[46]构建了一种水下气泡高速观测系统，提高了高速相机对水下气泡拍摄的成像质量。汤华鹏[47]基于高速相机系统，提出了一种应对气泡变形的图像处理方法，提高了高速相机系统计算精度。HIMR[48]通过高速相机和工作台对物理模型管线中的滞气进行拍摄和处理，得到了滞气在有压管道中的生成规律及运动状态，并且考虑到管道弹性等相关因素的影响，得出了滞气产生的相关规律。WUYI WAN[49]为了研究气泡的临界起动流速，设计了极端条件下的物理试验模型，该模型具有多个连续的弯管，可以在管线内各个部分进行定量的充气以模拟管线在极端条件下排出滞气的能力，通过大量的试验得出，适当地减小管线的倾角和加大流速可以有效地排出管线中的滞留气团。

激光多普勒技术以光学多普勒效应为核心，通过测量流体中的粒子散射光的多普勒频移得到流场的速度方向和速度大小等数据，通过测量相位差获得粒径等数据。许兆峰[50]基于激光多普勒技术设计了一套水气两相流观测系统，该系统提高了被观测气泡体积及流速的精度。TOKUHIRO[51]运用激光多普勒技术对流场中的气泡进行了观测和研究，结果表明在流场中加入带有标记的粒子，在激光的照射下通过CCD相机和工作站处理可得到需要的流场参数，同时还测得了气泡的运动轨迹及形态变化规律。JIGNESH THAKER[52]利用激光多普勒技术进行水中夹带气泡的试验，观测到气泡和流体之间存在较大的速度差，得出了液膜和气泡之间有较高的剪切应力等结论。

粒子图像技术是利用图像处理技术和计算机技术，拍摄连续两帧粒子的图像并经过计算机进行计算得到流场等数据。BIRVALSKI等[53]运用二维粒子图像量(PIV)技术，对管道中的气液两相流进行了试验和观测，测得了模型中的流场图像和相关的参数。MEYER等[54]学者运用PIV技术对气液两相流进行了观测，并获取了液膜的速度分布。黄浩成等[55]学者通过PIV技术观测了有压管道的流场，并对管道内的滞气进行了观测和研究，获取了大量的数据，分析和研究表明，当滞气的体积足够大时，排出这些滞气的流速的增幅会减小；坡度越大，排出滞气的流速将会变大。ZIQI GONG[56]使用PIV技术，测得了在不同条件下气泡上升的瞬时速度、气泡周围的流场和气泡的形态变化，得出气泡在疏水壁附近上升尾流较小的结论。相比于传统的二维粒子图像测量系统(PIV)只能得到二维平面的速度场的局限性，体三维(V3V)粒子图像测量系统可以测量出瞬态的三维速度场。FRANCIS C. K[57]应用体三维(V3V)系统观测了四十分之一坡度的湍流流场，得到了湍流的横轴水平涡流和纵轴垂直涡流。REDHA WAHIDI[58]使用体三维(V3V)系统测得了雷诺数为28000条件下流体中气泡运动的试验，得到了气泡周围的三维流场。通过体三维(V3V)技术能更好的观测出气泡起动临界流速。

4 结 论

长距离有压输水管道因其线路布置相对复杂、运行工况多、用途广泛等特点，需要高效、安全的运行模式，而滞气会对其安全产生严重的影响。长距离供水工程的规模相对较大，并且关系到大范围的工业生产需求和居民用水需求，如果出现事故造成停止供水，风险损失不可估量。因此对于有压输水管道中气泡起动临界流速需要更加深入和系统的研究，现有以下几点结论：

(1)在理论研究方面，目前对于有压管道中的气泡起动临界流速，不同研究结果得到的规律差异很大，相关机理尚不明晰，对于气泡体积等因素对气泡起动临界流速影响的研究成果较少。通过引入气泡动力学模型，结合有压输水系统中气泡的实际情况，建立包含气泡体积和表面张力等因素的气泡受力模型，可进一步研究上述因素对气泡起动临界流速的影响。

(2)在数值模拟方面，对于有压长输水管道中气泡起动临界流速，目前的数值模拟大多采用单一的模型进行计算，如VOF模型，该模型的优点是可以有效的模拟气液两相流中流场的变化情况，但也会出现计算误差相对较大等问题。而采用level set模型虽然也能得到流场内的气泡运动特性和形态变化规律，但在复杂的流场中，会出现严重的质量不守恒的情况。而耦合模型CLSVOF模型、VOSET模型就很好的克服了两种单一模型的缺点，并且结合了二者的优点，是未来数值模拟研究的趋势，目前运用耦合模型计算有压输水管道中气泡起动临界流速的研究相对较少。

(3)在物理模型试验方面，目前国内外对有压长输水管道中气泡的起动临界流速的研究大多集中在流速、倾角、管径等单一因素的影响，缺乏气泡体积、流速、倾角和管径等综合因素对气泡起动流速的影响及定量分析成果。