地质导向钻井轨迹控制技术研究
林 昕,苑仁国,韩雪银,陈玉山,于忠涛,刘素周
中海油能源发展股份有限公司工程技术分公司
0 引言
导向钻井轨迹精细控制是实现复杂油气藏勘探开发的关键技术之一,包括几何导向和地质导向两类。前人的研究大多集中在前者,对于后者研究较少[1-4]。地质导向区别于几何导向,其轨迹控制存在调整频次高、要求响应及时以及定向参数范围小等特点[2]。
为此,在已有的几何导向轨迹控制研究基础之上,研究了一种适用于地质导向钻井轨迹控制的技术,包括地质导向决策、几何导向指令、定向钻进参数和随钻测量监控四个模块(如图1所示),其中随钻测量监控模块引入机器学习相关技术实现对施工效果的实时监控。

图1 地质导向钻井轨迹控制流程图
1 地质导向决策
地质导向决策的依据是基于导向模型关键参数。如图2(a)所示,圆点代表钻头,导向模型关键参数包括钻头位置、地层厚度和倾角夹角,其中倾角夹角是指地层倾角和钻头井斜之间的夹角,通过分析关键参数和导向目标轨迹摆放位置之间的相对关系得到导向指令[5-6]。
目前绝大多数地质导向作业是基于垂向(井斜)上的调整,很少涉及横向(方位)上的调整。文章仅讨论垂向调整的控制,输出的指令类型分为:增斜、稳斜、降斜以及地质停钻。如图2(b)所示,展示了降斜、稳斜和增斜三种导向场景。图中红色虚线所示为导向目标轨迹摆放位置,黑色点划线为预测轨迹调整路线。如果在导向动力工具最大施工极限下仍无法避免钻出目的层顶底板,则需要地质停钻[5-6]。
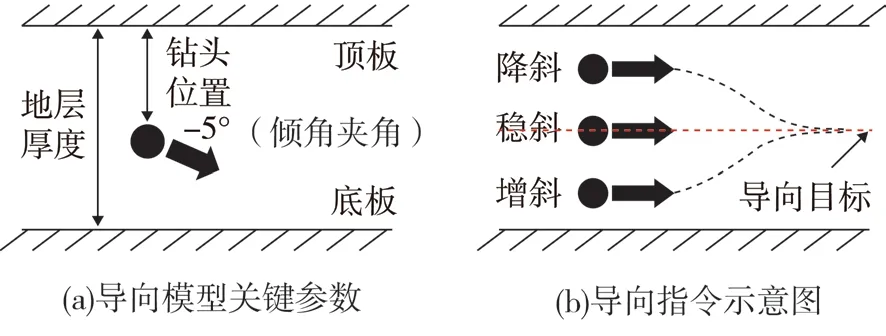
图2 地质导向决策
可以发现地质导向决策输出的指令形式是定性的,无法直接应用到工程作业,需转换成定量的几何导向指令才可以应用到现场施工当中。
2 几何导向指令
通过对现场作业流程进行分析,提出如下导向指令转换方案: 根据导向模型关键参数获取目标井斜值和井斜变化率,再结合钻井设计获取目标方位值和方位变化率;在优先满足井斜调整的前提下,对方位进行设置。
根据当前行业通用的最小曲率法,可以得到导向钻井轨迹的垂深/位移变化、井斜值和井斜变化率之间的近似关系,计算公式如下[3,7-8]:
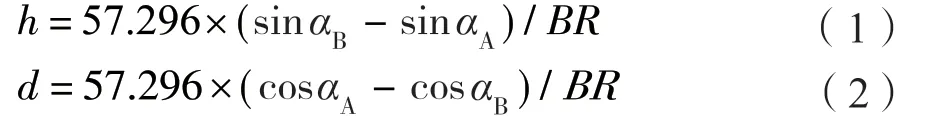
其中:
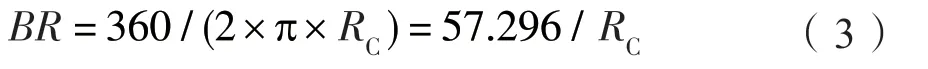
式中:αB—目标井斜角;αA—预测钻头井斜角;BR—井斜变化率,(°)/m;Rc—最小曲率半径长。
假设目标井斜不变,则BR直接影响轨迹的垂深和位移变化。BR越大,垂深和位移的变化越小。通常最大轨迹变化率(κmax)应小于导向动力工具的最大施工能力,由作业者在钻井设计中明确具体数值,以保障工程安全。如图3所示,在最大轨迹变化率下得到h>D或D+h>H时,说明轨迹存在钻出目的层的风险,需实施地质停钻,并获取更高作业权限。
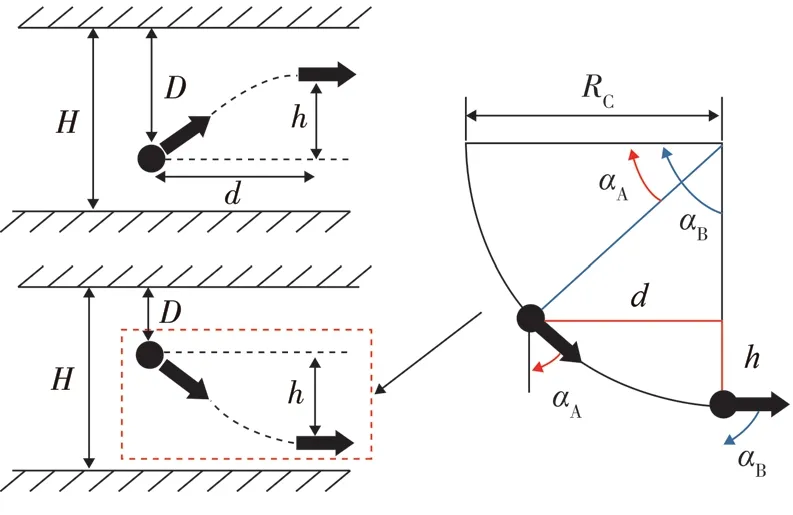
图3 井斜变化与垂深、位移关系示意图
这里需要明确目标井斜区别于上文所述的目标轨迹摆放位置的作用。通常设置目标井斜为地层倾角,调整至目标井斜后,需要进一步微调轨迹使之回到目标轨迹摆放位置,如图2(b)所示。
3 定向钻进参数
当前主流的导向动力工具主要包括螺杆和旋转导向。由于工作原理不同,定向参数存在差别。其中螺杆的定向参数为工具面和滑动段长(m),旋转导向的定向参数为工具面和力强度。两种工具分别通过两项参数来实现对导向轨迹变化率的控制[9-10]。
首先,工具面的角度由式(4) ~式(6)计算得到[3,7-8]。基于井斜优先调整的指令转换方案,BR确定后,由公式(4)得到的TR代入式(5),所得值应小于设定的κmax。
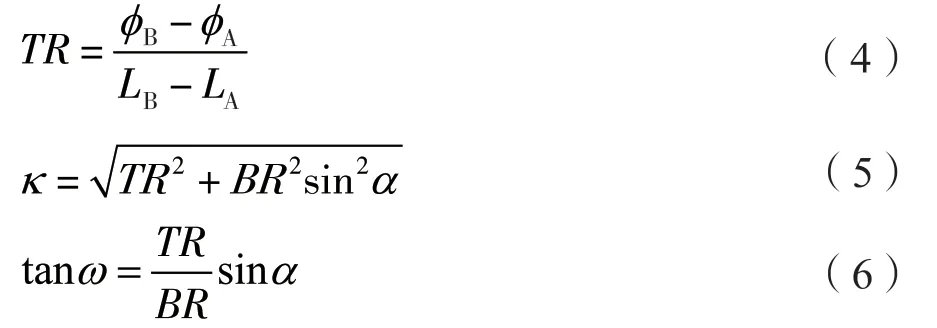
式中:TR—方位变化率;—目标方位角;—预测钻头方位角;LB—目标方位的斜深;LA—当前钻头位置斜深;κ—轨迹变化率;α—井斜角;ω—工具面。
其次,滑动段长或力强度的设置取决于实时分析。导向钻进过程中,κ呈现非线性响应的特征,即指令不变条件下钻进段越长,κ值越高,最终稳定在工具极限导向能力附近[9];此外地层变化以及工具面不稳定等因素直接影响施工效果。因此滑动段长或力强度的设置应建立在对实际施工效果的准确评估和预测上。为此,添加了随钻测量(MWD)监控模块,通过预测轨迹变化率分析施工效果,进而指导滑动段长或力强度的设置。
4 随钻测量监控
随钻测量监控的主要影响因素是MWD盲区长度。由国外公司主导的随钻工具如近钻头短节、旋转导向等已实现MWD零长0.5 ~ 1.5 m。近钻头测量减少了MWD盲区长度,预测精度更高,因此能有效分析施工效果,成为目前解决导向轨迹控制问题的优选方案。参考文献[11-12]介绍了运用近钻头测量技术解决深部(>5 000 m垂深)、超薄(<0.5 m地层厚度)地层的地质导向钻井施工,最终目的层钻遇率可以保持在90%以上。
大多数地质导向井仍然面临MWD零长较长的问题,如螺杆的MWD零长达到6 ~ 15 m,Vortex旋转导向(旋转导向+直螺杆)零长达到10 ~ 20 m[13]。为此,研究了基于机器学习的高斯过程回归(GPR)算法,实现在导向钻进过程中根据实时MWD数据监控施工效果。该方法包括构建MWD深度序列样本和GPR算法应用两个步骤。
4. 1 构建MWD深度序列样本
构建用于机器学习的MWD深度样本序列[14],建立训练集样本序列:
D = {(xi, yi) |i= 1, 2, …,n-p+1} = (X,Y) (7)式中:X—输入矩阵;Y—输出矩阵;x—工具面和力的乘积;y—轨迹参数(井斜或方位);p—传感器测量零长。
每条样本代表当前轨迹参数测量值(yn-p+1)、测量盲区定向参数数组(x∈Rd,d=p-1)以及预测井底钻头位置轨迹参数值(yn)的对应关系。定向参数以及轨迹参数均按照相同的测量间隔,根据测量深度顺序排列。
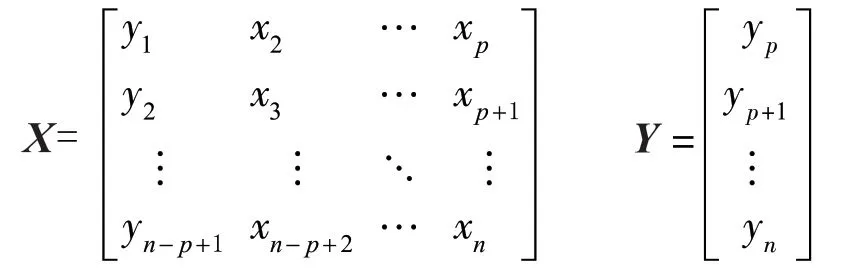
利用机器学习的回归分析可以学习输入矩阵X与输出矩阵Y之间的函数映射关系,并预测新测点的可能输出值;导向钻进过程中,随着MWD数据的更新不断生成新的训练集样本数据,并对算法模型进行重新学习训练。通过算法模型微调,消除岩性变化等因素对预测精度的影响。
4. 2 GPR算法应用
高斯过程(GP)是基于统计学理论发展起来的通用机器学习方法。GPR算法是通过定义GP来描述函数分布并在函数空间进行贝叶斯推理。GPR作为机器学习回归分析方法,对于处理小样本以及非线性等问题适应性较好;具有容易实现、超参数自适应获取和预测输出具有概率意义等优点[14-17]。
图4 ~ 图5展示了分别以螺杆和旋转导向作为导向动力工具情况下随钻监控测量模块的现场应用效果,其中,螺杆MWD零长15 m,Vortex旋转导向的MWD零长17 m。选取了相似作业工况井段进行对比。
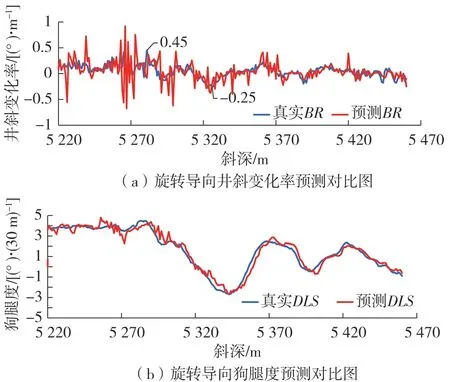
图4 旋转导向井斜变化率预测对比图

图5 螺杆井斜变化率预测对比图
对比两种工具的真实BR数据,可以发现BR波动明显,个别数据点出现峰值。旋转导向相对螺杆BR变化更剧烈,这是由于旋转导向的工具面比螺杆稳定,钻进过程中更容易出现轨迹变化率的非线性响应特征。GPR算法能够预测BR的变化趋势,但是峰值数据点的预测结果更激进。
以狗腿度(DLS)作为轨迹变化率的标准单位(°)/30 m,监测结果数据分析如表1所示。GPR算法对狗腿度预测的决定系数R2达到95%以上,可以有效指导轨迹调整的定向参数设置,进而提高轨迹控制精度。

表1 螺杆及旋转导向施工狗腿度监控结果分析
5 结论
(1)梳理了地质导向决策流程,提出了基于导向模型关键参数来分析地质导向决策指令的方法,总结了从地质导向到几何导向指令转换的方案。实现从定性的地质指令转换为定量的定向参数。
(2)利用随钻测量监控的方法预测施工效果,进而提高地质导向钻井的轨迹控制精度。为满足螺杆和旋转导向等导向动力工具使用环境下的应用,提出如下监测方案:建议采用具备近钻头测量功能的钻具组合;针对MWD零长较长的情况,可采用基于GPR的随钻预测算法实现对施工效果精确监测。

