基于预测误差自适应编码的图像加密可逆数据隐藏

杨尧林 和红杰 陈 帆 原长琦

1(西南交通大学信息科学与技术学院 成都 611756)

2(北京电子技术应用研究所 北京 100091)

(ylyangwr＠foxmail.com)

随着计算机的发展应用,更多的用户选择把数据上传至云端存储,云存储使数据的所有权和管理权分离,使得云存储中数据安全以及个人隐私保护引起了人们的关注,加密图像可逆数据隐藏(reversible data hiding in encrypted image,RDH-EI)可为云存储中图像数据的安全提供技术支持[1-2].与传统的明文域可逆数据隐藏不同,RDH-EI首先对图像进行加密,在加密图像中实现可逆的数据隐藏.其中,图像加密有效避免了原始图像内容的泄露.同时,密文图像中附加数据的提取可用于图像真实性认证,来源追踪及隐私保护等多种应用场景[3-4].

现有RDH-EI可分为2类:加密前预留空间(reserving room before encryption,RRBE)[5-9]和加密后腾出空间(vacating room after encryption,VRAE)[10-18].RRBE-RDHEI可利用明文图像像素间的相关性提高嵌入容量,但增加了图像拥有者的操作难度,不仅需要对原始图像进行加密,还要在加密前执行预处理操作,这对于普通用户来说是难以实现的.而在VRAE-RDHEI中,图像拥有者只需要执行图像加密即可,减小了图像拥有者的技术需求.

在已有的VRAE-RDHEI算法中,根据嵌入方法的不同可分为3类:1)采用低位翻转[10-12],通过翻转加密图像像素的最低有效位(least significant bit,LSB)嵌入附加数据.该类算法操作简单,可获得较高的直接解密图像质量,但数据提取与图像恢复2个步骤不可分离,且图像恢复阶段不能完全可逆.2)采用传统RDH嵌入附加数据,其中直方图移位[13-15]应用较广泛,通过寻找像素值或误差值的峰值点与零点值,将像素值进行小幅度修改实现信息的嵌入.该类算法能够实现完全可逆,但嵌入容量相对较小.3)采用编码无损压缩,使用编码表对图像进行压缩,从而腾出空间用于嵌入附加数据.该类算法嵌入容量较高,得到多数学者的关注.Yi等人[16]提出一种参数加密域可逆数据隐藏(parametric reversible data hiding in encrypted images,PRDHEI)算法,设计了2种嵌入编码策略,在嵌入过程中选取嵌入率较高的编码表进行标记压缩.在图像完全恢复的情况下,平均嵌入率达1.19 bpp.为进一步提高嵌入率,Yi等人[17]修改了嵌入过程中使用的编码表.在二叉树逻辑结构的基础上实用化,提出了参数二叉树标记(parametric binary tree labeling,PBTL)的方法,将加密后图像的像素根据预测误差及选取的参数标记为可嵌入像素和不可嵌入像素2种,标记后压缩的空间可用来嵌入秘密信息.该算法的平均嵌入率可达1.68 bpp,相较于文献[16]的嵌入率提高0.49 bpp.上述2种方案对可嵌入像素预测误差的编码长度是相等的,但对分布不均匀的预测误差,变长编码要比定长编码具有更高的压缩率.在Fu等人[18]提出的自适应编码策略算法中,使用预先设定的哈夫曼编码表对加密后图像块的最高有效位(most significant bit,MSB)分类标记,平均嵌入率可达1.81 bpp.该方案中编码表涵盖了一个块中最多存在4种不同MSBs的情况,但对纹理图像,包含4种MSBs以上的块数是较多的,将其全部作为不可嵌入块将会导致嵌入率降低.综上所述,现有VRAE-RDHEI文献中使用的编码表大多是预先设定的,未结合图像自身的特征,因此根据图像自身像素值特征选取适合的编码策略是提高嵌入容量的一种有效解决方案.

提高嵌入容量是已有RDH-EI算法研究的主要内容,同时,加密算法的安全性也逐渐被研究者们关注.上述算法中,文献[7-12]采用了位异或加密方法,加密后的熵值较高,密文图像类似随机噪声,但加密前后像素位置并未发生变化,不能抵抗Khelifi[19]提出的唯密文攻击.为抵抗这类唯密文攻击算法,多位研究者提出块置乱及相应改进算法[13-18].在文献[13]中,采用块内置乱与块间置乱,该方法中像素值并未发生改变,不能抵抗Li等人[20]提出的已知明文攻击.在文献[16-17]中,块间置乱与像素调制后虽然像素的位置与像素值均发生变化,但块内像素的相对差值依旧会保留.在文献[15]中,块间置乱与块内异或后由于块内像素进行异或运算的二进制值序列相同,所以块内像素的部分相关性将会保留,且在块间置乱前后,加密图像块与原始图像块是一一对应的关系.上述加密算法中,原始图像与加密图像块之间存在的关联性与块内像素的相关性成为攻击者破解加密图像的依据.为提高加密算法的安全性,打乱置乱操作保留的一一对应关系是需要研究的关键问题.

为提高算法嵌入容量的同时兼顾加密算法的安全性,本文提出一种基于预测误差自适应编码的图像加密可逆数据隐藏算法.在加密阶段,采用误差维持加密算法,包括块间置乱、像素调制以及分组置乱3个步骤.与未加入分组置乱的加密算法相比,增加了加密前后图像的特征值差异块数,提高了加密图像的安全性,同时未改变加密图像的整体预测误差分布.在嵌入阶段,根据加密图像的预测误差分布自适应编码(adaptive coding,AC),生成哈夫曼编码表后对像素进行标记压缩,能实现较大的嵌入容量.且哈夫曼编码具有唯一标识性,能无损提取附加数据与恢复原始图像,实现完全可逆.

1 基于预测误差自适应编码的RDH-EI

本文算法主要包括3部分:基于误差维持的图像加密;基于自适应编码的信息嵌入;数据提取与图像恢复.1)基于误差维持的图像加密.图像拥有者利用加密密钥Kenc对原始图像Iori执行块间置乱与像素调制,再将非中心像素分组置乱生成加密图像Ienc.2)基于自适应编码的信息嵌入.数据隐藏者根据加密图像Ienc的预测误差分布选取范围生成哈夫曼编码表,对图像进行标记后嵌入辅助数据与加密的附加数据生成携密加密图像Imark.3)数据提取与图像恢复.图像接收者根据持有的密钥可分别获得原始的附加数据或图像.下面对算法按上述3个部分进行详细描述.

1.1 基于误差维持的图像加密

在误差维持加密中,图像拥有者首先将图像分为非重叠块,对所有块执行块间置乱与像素调制;然后进行分组置乱,通过图像块的中心像素值将对应的非中心像素分组后,根据加密密钥将每组的像素进行置乱.具体操作描述如下:

1)块间置乱与像素调制

Step1.图像分块.将大小为A×B的原始图像Iori分为m个大小为3×3的非重叠块2,…,m),其中m＝A/3×B/3.

Step2.中间图像生成.根据加密密钥Kenc,采用文献[16]中的方案执行块间置乱与像素调制.若图像未被整除,则对边缘区域的像素进行异或加密,生成中间图像Iint,其中包含非重叠块2,…,m).

2)分组置乱

Step2.非中心像素分组置乱.将图像Iint中心像素值为p的图像块中非中心像素分为1组,生成分组序列.基于加密密钥Kenc产生1～n pnon互不相同的伪随机自然数序列T p＝.使用序列T p置乱对应的分组序列C p,得置乱后的分组序列D p为

Step3.加密图像生成.将置乱后的分组序列D p依次重新排列到图像Iint中心像素值为p的图像块中,生成加密图像Ienc.

本文误差维持加密算法中的分组置乱操作,将中间图像中心像素值相同块对应的非中心像素随机置乱.一方面,将块间置乱保留的原始图像块与加密图像块一一对应关系变为多对多的关系,攻击者难以确定原始图像块与加密图像块之间的关联,提高了加密图像的安全性.另一方面,同一个非中心像素在分组置乱前后所在图像块的中心像素值一致,即非中心像素与中心像素的预测误差值保持不变.

为更直观地描述加密过程,以图像大小为9×9,分块大小为3×3为例描述加密操作,如图1所示.图1(a)为原始图像,可分为4个像素块,灰色部分为中心像素;图1(b)为块置乱图像,由原始图像按置乱序列{3,4,2,1}执行块间置乱产生;图1(c)为中间图像,通过调制序列{1,2,7,6}对块置乱图像执行像素调制生成.最后根据中心像素的不同可分为3组,分别为中心像素值为101的非中心像素序列{101,102,104,104,105,106,104,109};中心像素值为105的序列{104,104,102,106,102,106,105,105,108,108,110,115,108,116,105,106};中心像素值为110的序列{110,109,108,108,115,108,109,106}.分别按置乱序列{2,5,8,6,3,1,4,7},{5,16,14,3,9,10,4,15,12,1,6,8,11,2,13},{5,7,3,6,4,2,1,8}执行置乱并重新排列后生成如图1(d)所示的加密图像.

1.2 基于自适应编码的信息嵌入

当数据隐藏者接收到加密图像后,首先根据预测误差分布选取范围对像素进行分类;然后根据各类像素概率生成并保存哈夫曼编码表;最后使用编码表对像素进行标记与附加数据嵌入.具体操作描述为:

1)像素分类

Step1.临界概率值确定.根据同层概率相同的哈夫曼树中编码概率与编码长度的关系确定临界概率值.假设临界概率表示为plim,编码长度为l,则两者的关系为

对于8 b深度的灰度图像像素值,哈夫曼编码长度不能超过8 b,则编码临界概率至少满足plim＝0.00390625.

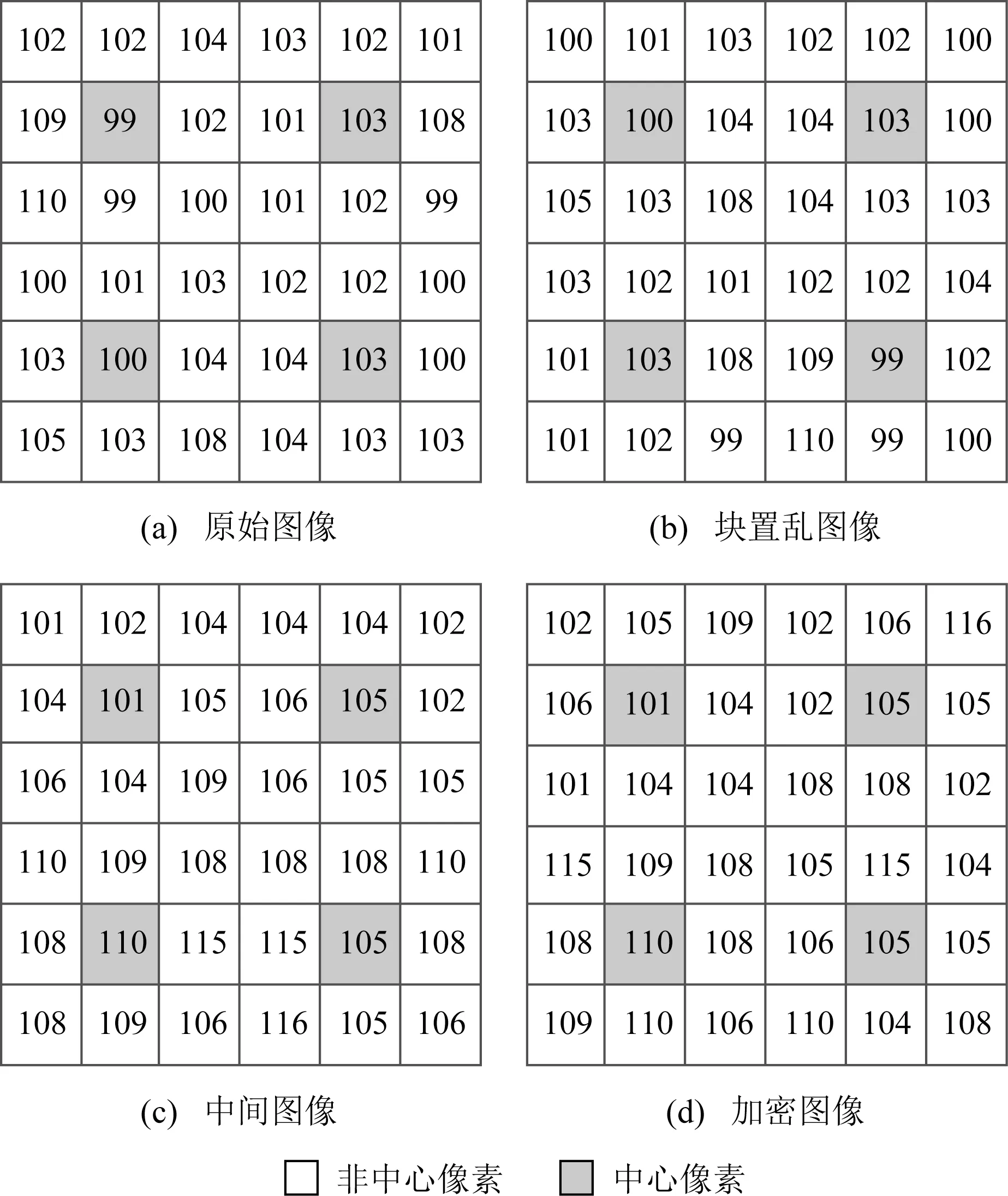
Fig.1 Schematic of encryption process图1 加密过程示意图

Step2.预测误差计算.首先将加密图像Ienc分为m个大小为3×3的非重叠块然后将第k个块的中心像素定义为参考像素,记为其余的8个像素定义为非参考像素,记为(i＝1,2,…,8).则第k个块中第i个非参考像素与参考像素的预测误差为

Step3.非参考像素分类.通过直方图统计整幅加密图像预测误差值为e(e∈[－255,255])的数量n e,对应概率为p e.由临界概率值plim确定小于0的预测误差下限α与大于0的预测误差上限β.根据α和β将非参考像素分为2类,若第k个块中第i个非参考像素的预测误差满足:

2)编码表生成与保存

Step1.编码表的生成.将所有不可嵌入像素归为一类,则其概率为

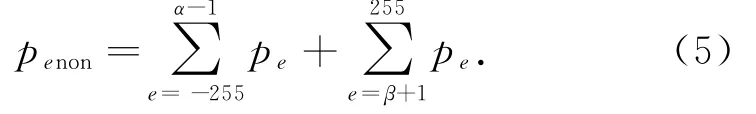
可嵌入像素根据预测误差不同可分λ＝β－α＋1类,其概率为p e(e＝α,α＋1,…,β－1,β),则非参考像素共分为λ＋1类.根据λ＋1类像素的概率生成哈夫曼编码表,其中,不可嵌入像素对应的编码为f0,λ类可嵌入像素对应的编码为f i(i＝1,2,…,λ).

若编码表中存在编码的长度大于8 b,将预测误差下限α加1,预测误差上限β减1,对非参考像素重新分类后再次执行本步骤.

Fig.2 Storage form of Huffman coding table图2 哈夫曼编码表存储结构

其中,a,b,c i(i＝0,1,…,λ)分别为|α|,|β|,d i对应的二进制序列.哈夫曼编码存储长度为η.

Step3.编码表保存.将哈夫曼编码表通过位替换存储在前nref个块的参考像素中,当η不足8的倍数时,在末尾补充长度为8×nref－η的比特‘0’序列.被替换参考像素的原始比特组合为w.

3)像素标记与附加数据嵌入

Step1.不可嵌入像素标记.通过位替换将不可嵌入像素的前d0位MSBs替换为f0,剩余的8－d0位LSBs保持不变.同时将被替换的原始MSBs组合的比特流记为v,其长度为ξ.

Step2.可嵌入像素标记与附加数据嵌入.用长度为d i(i＝1,2,…,λ)的编码f i替换可嵌入像素的MSBs,剩余的8－d i位LSBs嵌入总隐藏数据φ,生成携密加密图像Imark.

在上述总隐藏数据φ中,除加密的附加数据ϕ外,还包括一部分图像的原始数据作为辅助数据用于图像恢复.其中,ϕ为原始附加数据ρ通过数据隐藏密钥Khid异或加密后生成的比特流.辅助数据包括2部分:保存编码表时被替换的前nref个块的参考像素原始比特流w;不可嵌入像素的原始d0位MSBs组成的比特流v.将总隐藏数据长度定义为ζ,则本算法的嵌入率rate为

综上所述,在基于自适应编码的嵌入过程中,通过加密图像整体的预测误差分布特性自适应地生成哈夫曼编码表,对像素进行标记压缩腾出空间用于数据嵌入.其中,哈夫曼编码的唯一标识性成为数据提取与图像恢复阶段对携密加密图像中的非参考像素进行分类的依据.

1.3 数据提取和图像恢复

图像接收者得到携密加密图像Imark后,根据持有密钥的不同,其权限也不同.拥有数据隐藏密钥Khid,可提取原始的附加数据ρ;拥有加密密钥Kenc,可恢复原始图像Iori.

1)附加数据提取

Step1.分类界限提取.将携密加密图像Imark分为m个大小为3×3的非重叠块m),并从图像块的参考像素中分别提取8 b恢复预测误差下限α与预测误差上限β,确定可嵌入像素类数λ＝β－α＋1.

Step2.编码表重建.从I(3)mark与其随后块的参考像素中依次提取λ＋1个编码的编码长度d i(i＝0,1,…,λ)与编码f i,重建哈夫曼编码表,同时统计存储编码表被替代的参考像素个数nref.

Step3.附加数据的提取.根据重建的哈夫曼编码表与非参考像素的标记位,将非参考像素分为可嵌入像素与不可嵌入像素,对不可嵌入像素,统计其数量n enon,对可嵌入像素,提取除标记位外的8－d i位LSBs,得到总隐藏数据φ.可知,总嵌入数据的前8×nref位为保存编码表时被替换的参考像素原始比特流w,中间n enon×d0位为不可嵌入像素的前d0位MSBs组成的比特流v,剩余位为加密的附加数据ϕ.最后用数据隐藏密钥Khid将ϕ进行异或解密可得原始的附加数据ρ.

2)图像恢复

Step1.加密像素值的恢复.首先,与附加数据提取一致,提取w与v.然后,用w恢复前nref个块的原始参考像素.非参考像素中,对不可嵌入像素,用v恢复原始像素的前d0位MSBs;对可嵌入像素,由编码表中编码与预测误差的一一对应关系可得出预测误差值,进而恢复加密图像Ienc的原始像素值.

Step2.原始图像的恢复.加密过程具有可逆性,使用加密密钥Kenc对加密图像Ienc依次执行逆分组置乱、逆像素调制、逆块间置乱即可恢复原始图像Iori.

综上所述,数据提取与图像恢复阶段能够无损重建哈夫曼编码表,进而根据所持密钥无损地提取附加数据或恢复原始图像.

2 实验结果与分析

下面通过实验来验证分析本文算法的性能,主要从4个方面:1)误差维持加密算法分析;2)嵌入容量分析;3)可逆性分析;4)运行时间分析.在实验过程中选取如图3所示的大小为512×512的8幅灰度测试图像,分别为Lena,Jetplane,Barbara,Peppers,Boat,Lake,Crowd,Baboon.同时使用包含1 338幅的UCID[21]与包含10 000幅的BOSSbase[22]这2个图像库进行实验分析,其中,UCID中所有图像均转变为512×512的灰度图像.

Fig.3 Test image图3 测试图像

2.1 误差维持加密算法分析

误差维持加密包括块间置乱、像素调制和分组置乱3部分,其中,分组置乱操作是根据所在块中心像素值的不同,将非中心像素分组后置乱.该操作能改变非中心像素所在的块,打乱块间置乱操作保留的原始图像与加密图像中各图像块间的对应关系,提高加密算法的安全性.且分组置乱前后非中心像素所在块的中心像素值相等,故整体的预测误差分布不变.下面从这2方面对加密算法进行分析测试.

1)整体预测误差分布

为证明分组置乱是否会造成整体预测误差分布发生变化,对分组置乱的原理进行分析.在分组置乱的过程中,所有相同中心像素值所对应的非中心像素分为一组进行置乱,此时即使改变非中心像素的位置,它们所对应的中心像素值依旧保持不变.而预测误差值是将非中心像素值减去中心像素值,因此只要中心像素值未发生变化,预测误差值均保持不变.以图1(c)(d)为例,在图1(c)中,中心像素值为105对应的非中心像素为{104,104,102,106,102,106,105,105,108,108,110,115,108,116,105,106},预测误差为{－1,－1,－3,1,－3,1,0,0,3,3,5,10,3,11,0,1}.而在图1(d)中,中心像素值为105对应的非中心像素预测误差为{－3,1,11,－3,0,3,3,－3,0,10,－1,1,0,5,－1,3},可以看出,图1(c)中间图像与图1(d)加密图像的预测误差分布一致.

以Lena图像为例,统计有无分组置乱加密图像(中间图像与加密图像)的预测误差分布,结果如图4所示.可以看出,两者的预测误差分布相同,说明加入分组置乱后并未改变整体的预测误差分布,即不会影响图像的嵌入容量.

Fig.4 Prediction error distribution with or without group scrambling图4 有无分组置乱的预测误差分布

2)加密算法安全性分析

为评价加密图像的安全性,定义原始图像与加密图像的特征值差异块数作为衡量指标,其中,图像块的特征值是该块所有的非中心像素与中心像素差值绝对值的总和.当原始图像与加密图像的特征值差异块数越多时,表明加密图像的安全性越高.计算指标的具体操作为:

1)计算图像块特征值,定义第k个块的特征值为8个非中心像素的预测误差绝对值总和

2)通过直方图统计原始图像、加密图像中图像块特征值为pe的数量.由于非参考像素的预测误差值e∈[－255,255],得pe的取值范围为

3)统计原始图像与加密图像之间的特征值差异块数dif:

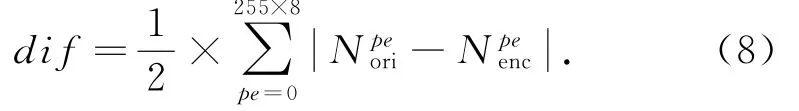
为验证本文加密算法的安全性,以加入分组置乱的加密图像与未加入分组置乱的中间图像进行对比.

首先,以图1为例,图1(a)中原始图像各块的特征值分别为{36,17,27,10},图1(c)中间图像各块的特征值分别为{27,10,17,36},图1(d)加密图像各块的特征值分别为{27,27,17,21}.此时原始图像与中间图像特征值差异块数为0,块间置乱序列能够被唯一确定,而原始图像与加入了分组置乱加密图像的特征值差异数为2,存在一半的块无法确定对应关系,因此加入分组置乱能提高加密图像的安全性.

然后,以8幅测试图像为例,统计原始图像与中间图像的特征差异块数difoi,原始图像与加密图像的特征差异块数difoe,结果如表1所示.可以看出,difoe相较于difoi增加了3～4倍,即加入了分组置乱后的加密图像与原始图像的特征值差异块数较多,难以确定原始与加密图像中图像块的对应关系,加密图像的安全性得到提高.

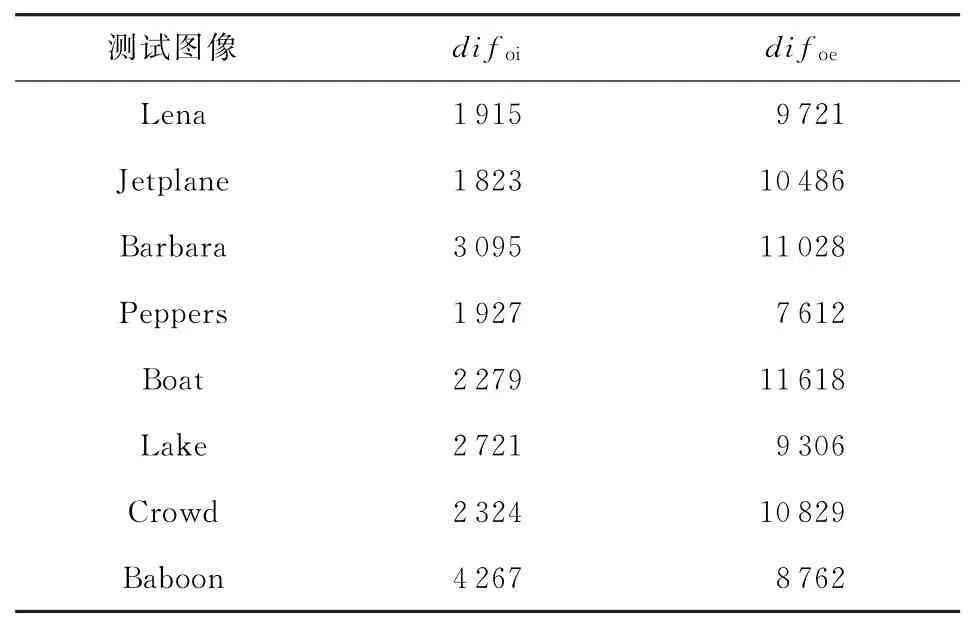
Table 1 Comparison of Eigenvalue Difference Blocks表1 特征值差异块数对比

下面从密钥空间的角度对本文加密算法的安全性进行分析.假设图像大小为A×B且分块大小为3×3,则块间置乱的密钥空间ψ1为

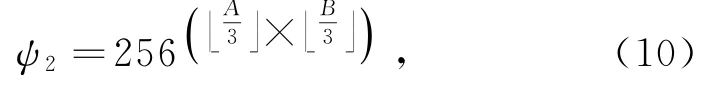
像素调制的密钥空间ψ2为

像素调制后图像的像素值近似均匀分布,故分组置乱的密钥空间ψ3为

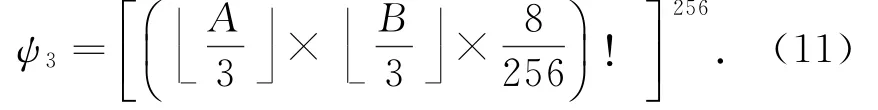
本文加密算法的密钥空间为ψ＝ψ1×ψ2×ψ3.当图像大小为512×512且分块为3×3时,可能生成28900!×25628900×(903!)256种不同的加密图像.在这种情况下,若没有加密密钥,攻击者很难将加密图像进行恢复.

综上所述,误差维持加密算法中,在加入分组置乱后未改变图像整体预测误差分布,但增加了加密图像与原始图像的特征值差异块数,提高了加密图像的安全性.

2.2 嵌入容量分析

由RDH-EI算法易知,总嵌入容量与压缩率正相关,即压缩率越高,总嵌入容量越高,嵌入率也就越高.以8幅测试图像为例,将文献[17]的PBTL在最大嵌入容量时的相关数据与本文进行对比,结果如表2所示.其中,ζ为总隐藏数据的长度,即总嵌入容量;ξ为不可嵌入像素原始MSBs比特流的长度,η为哈夫曼编码表存储结构的长度,ξ与η之和为辅助数据的总长度;γ为附加数据的长度,即净嵌入容量;根据式(6)计算得到图像的嵌入率rate.分析Lena图像的测试数据可知,本文算法相较于PBTL,ζ提高99.89 Kb,ξ提高7 713 b,η提 高286 b,γ提高92.07 Kb,嵌入率rate提高0.36 bpp.统计8幅测试图像的平均值,本文算法的ζ提高70.27 Kb,ξ降低14.71 Kb,η提高364 b,γ提高84.62 Kb,嵌入率rate提高0.33 bpp.

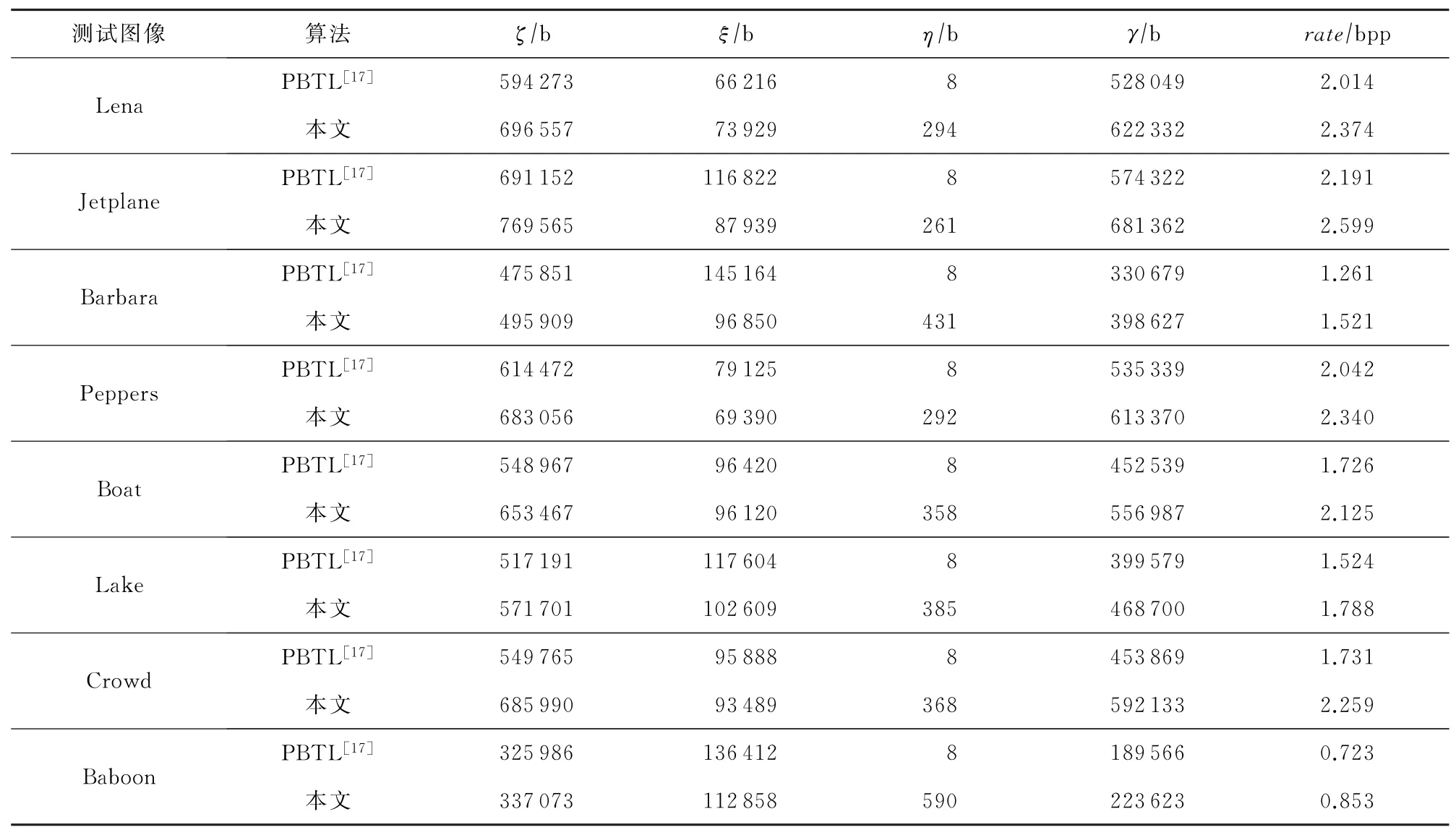
Table 2 Comparison of the Embedding Capacity and Auxiliary Data Between the Algorithm of Ref[17]and Our Algorithm表2 文献[17]与本文算法的嵌入容量与辅助数据对比

为进一步验证本算法的嵌入容量优势,选取3篇同类文献(VRAE-RDHEI)进行统计对比,包括Yi等人[16]的PRDHEI算法、Yi等人[17]的PBTL算法和Fu等人[18]的自适应编码算法.其中,文献[16]采用算法完全可逆时的嵌入容量;文献[17]选取测试图像的最大嵌入容量;文献[18]设定分块大小为4×4、MSB位数H＝5、阈值T＝4时的嵌入容量.以8幅测试图像为例,对比文献与本文算法最大嵌入容量如表3所示.分析表3数据可知,本文的嵌入容量均高于现有文献.结合表2分析,对较平滑的Jetplane图像,预测误差分布相对集中,压缩率较高,嵌入率相较3篇对比文献分别提高了1.324 bpp,0.408 bpp,0.406 bpp;对于较纹理的Baboon图像,预测误差分布较均匀,压缩率较低,相较对比文献提升较少,分别为0.853 bpp,0.130 bpp,0.391 bpp.对8幅测试图像的嵌入率计算平均值可得,本文算法的平均嵌入率相较对比文献分别提高了1.262 bpp,0.330 bpp,0.364 bpp.

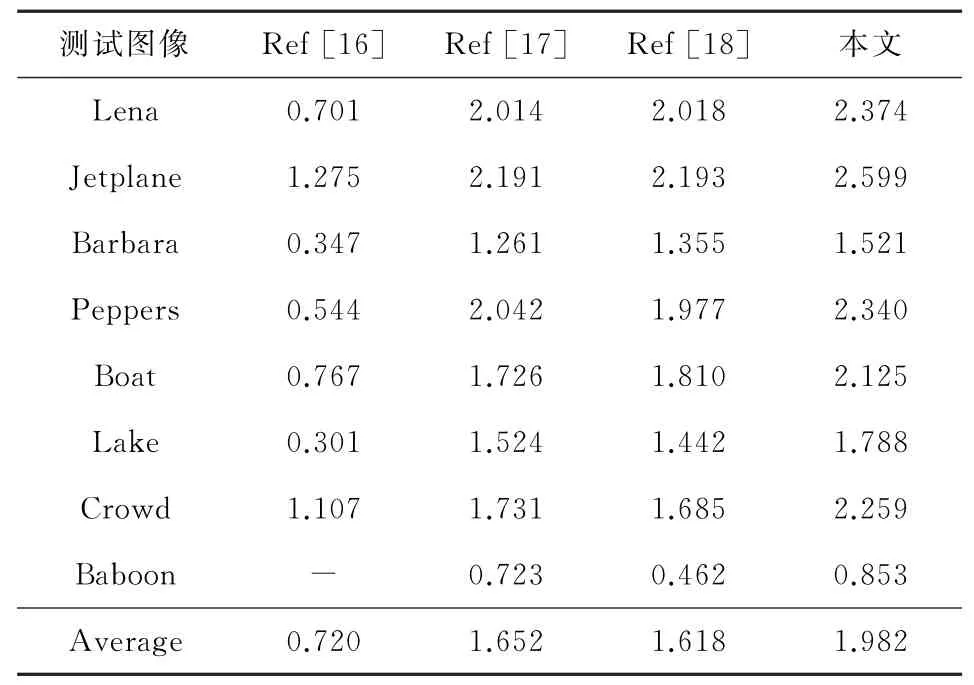
Table 3 Comparison of Maximum Embedding Rate表3 最大嵌入率对比 bpp

为更好地说明本文算法的嵌入率高于现有算法,对UCID的1 338幅图像与BOSSbase的10 000幅图像分别测试,计算每个图像库的平均值作为算法的平均嵌入率,得到本文与文献[16-18]在2个图像库的平均嵌入率如表4所示.为方便测试,文献[16]设定分块大小为3×3,α＝5,β＝2时的嵌入容量作为最大嵌入容量.通过对比表4数据可知,对UCID图像库,本文的平均嵌入率相较于对比文献分别提高1.115 bpp,0.626 bpp,0.492 bpp.对BOSSbase图像库,分别提高1.251 bpp,0.881 bpp,0.662 bpp.

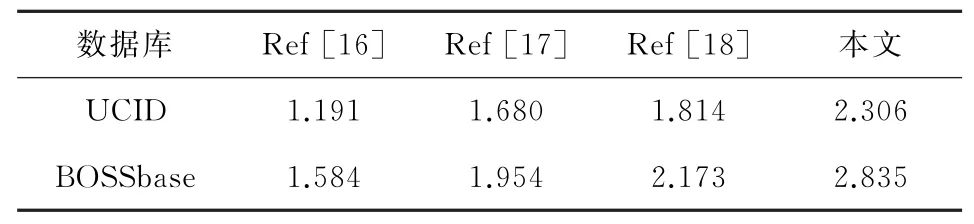
Table 4 Comparison of Average Embedding Rate of Database表4 图像库平均嵌入率对比 bpp

为可视化本文与对比文献在嵌入容量上的对比情况,从UCID与BOSSbase数据库中分别选取前200幅图像进行测试,结果如图5所示.可以看出,本文算法所得到的嵌入率要高于3篇对比文献.在UCID的200幅图像中,本文算法的平均嵌入率相较于文献[16-18]分别 提 高1.24 bpp,0.45 bpp,0.46 bpp;在BOSSbase的200幅图像中,本文算法的平均嵌入率分别提高1.24 bpp,0.71 bpp,0.58 bpp.

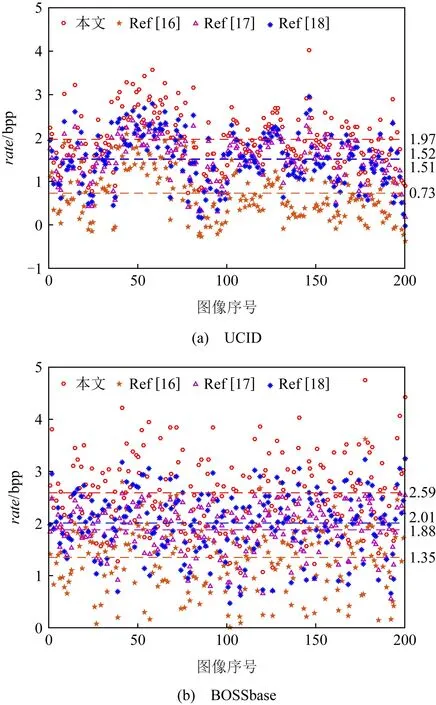
Fig.5 Comparison of the embedding rate between our algorithm and three state-of-the-art algorithms图5 本文算法与3篇现有算法的嵌入率对比

为对比分析本文AC方案与现有腾挪空间方法的性能,本文新增加2篇文献[7-8]RRBE-RDHEI对比分析.文献[7-8]均采用中值边缘检测(median edge detection,MED)方法预测,腾挪空间方法分别为提高的参数二叉树标记的可逆数据隐藏方案(improved reversible data hiding scheme in encrypted images using parametric binary tree labeling,IPBTL)和哈夫曼编码标记(Huffman coding labeling,HVLCL).在实验中,为公平起见,本文采用相同的MED预测方法得到预测图像,并按照文献[7]对算法的加密阶段进行调整.调整后算法中生成含标记加密图像的步骤描述为:1)生成预测误差分布图.将原始图像第1行与第1列作为参考像素进行MED预测生成预测误差分布图.2)图像加密.对原始图像进行异或加密生成加密图像.3)像素分组.结合本文的临界概率值与预测误差分布图,将非参考像素分为可嵌入像素与不可嵌入像素.4)像素标记.由本文的AC方案生成哈夫曼编码表,并构造出哈夫曼编码的存储结构自左至右保存到加密图像的第1行参考像素中.结合预测误差分布图对加密图像进行标记,将加密图像原始参考像素比特流及不可嵌入像素被替换的原始比特流嵌入可嵌入像素压缩出的空间,生成含标记的加密图像.最终,剩余空间可被数据隐藏者用于嵌入附加数据.

然后,分别使用IPBTL[7]、HVLCL[8]和本文的调整算法得到相应的最大嵌入容量,其中,IPBTL[7]设定α＝5,β＝3.8幅测试图像的对比结果如表5所示.以Lena图像为例,本文AC相较于IPBTL的总嵌入容量提高167.34 Kb,辅助数据提高17.24 Kb,净嵌入容量提高150.10 Kb,嵌入率提高0.587 bpp;相较于HVLCL的总嵌入容量降低543.00 Kb,辅助数据降低718.00 Kb,净嵌入容量提高175.01 Kb,嵌入率提高0.683 bpp.同理,计算8幅图像对比结果求取平均值可得,IPBTL的平均嵌入率为2.256 bpp,HVLCL的平均嵌入率为2.284 bpp,本文AC方案的平均嵌入率为2.842 bpp,相较于IPBTL和HVLCL分别提高0.586 bpp与0.558 bpp.

Table 5 RRBE-RDHEI Scheme Comparison of Test Image表5 测试图像的RRBE-RDHEI方案对比

为进一步说明本文AC方案优于现有的IPBTL[7]与HVLCL[8],以UCID与BOSSbase两个图像库为例进行实验,结果如表6所示.可以看出,在相同预测方法的基础上,本文的AC方案具有最高的嵌入容量,相较于IPBTL[7]提高1.11 bpp以上,相较于HVLCL[8]提高0.51 bpp以上.

Table 6 RRBE-RDHEI Scheme Comparison of Database表6 图像库的RRBE-RDHEI方案对比 bpp

2.3 可逆性分析

本文算法中,采用哈夫曼编码对像素进行标记,基于哈夫曼编码的唯一标识性,能够实现原始图像的可逆恢复.图6显示了Lena图像在本算法中的仿真结果.其中图6(a)为原始的Lena图像,图6(b)为加密图像,图6(c)为携密加密图像,图6(d)为恢复图像.使用峰值信噪比(peak signal-to-noise ratio,PSNR)与结构相似性(structural similarity,SSIM)作为评测算法的可逆性的指标,则恢复图像的PSNR为∞,SSIM为1,本文算法实现完全可逆.

Fig.6 Simulation results of Lena图6 Lena图像仿真结果

为进一步验证算法的可逆性,测试2个图像库的相关指标,如表7所示.可以看出,本算法在最大、最小嵌入率的图像中,以及图像库的平均情况下,恢复图像的PSNR均趋近于无穷,SSIM均为1,说明可以实现完全可逆.且本算法在2个图像库中的最高嵌入率可达5 bpp以上,平均嵌入率可达2.3 bpp以上.综上,本算法在实现高嵌入容量的同时能完全可逆恢复原始图像.

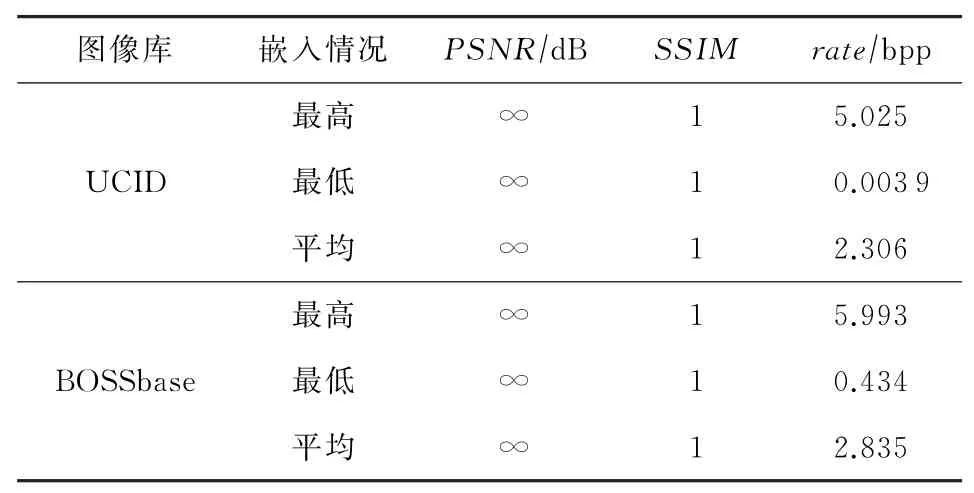
Table 7 Test Results of Database表7 图像库测试结果

2.4 运行时间分析

RDH-EI算法主要包括4个阶段:图像加密、数据嵌入、数据提取和图像恢复,其中,图像所有者用户主要执行图像加密算法,因此加密性能直接影响用户的体验.下面对本文加密算法的运行时间分析,并选择5篇文献作对比:文献[7]的异或加密;文献[13]的块间置乱与块内置乱加密;文献[17]的块间置乱与像素调制加密;文献[15]的块间置乱与块内异或加密;文献[18]的块间置乱、块内置乱与块内异或加密.

时间复杂度上分析说明:当图像大小为A×B且分块大小为s×s时,异或加密、块内异或、块内置乱与像素调制对所有像素执行了一次操作,时间复杂度为O(A×B),块间置乱的操作以块为单位进行,时间复杂度为O(A×B/s2),本文分组置乱操作中除参考像素外的其余像素均进行置乱,时间复杂度为(s2－1)/s2×O(A×B).

对各种加密算法进行实验对比,实验环境为:Windows 10操作系统(企业版2016)、MATLAB 2015a;硬件配置为Intel®CoreTMi5-6200U CPU＠2.30 GHz 2.40 GHz,4.00 GB内存(3.89 GB可用),64位操作系统的笔记本电脑.

实验测试图像:大小为256×256,512×512,1024×1024的图像;分块大小为2×2及3×3.运行时间统计10次求取平均值,结果如表8所示.可以看出,本文加密算法在提高算法安全性前提下,图像大小为512×512且分块大小为3×3时的运行时间为1.28 s,在可接受范围内.

Table 8 Comparison of Running Time of Encryption Algorithms表8 加密算法运行时间对比 s

3 结 论

本文提出一种基于预测误差自适应编码的图像加密可逆数据隐藏算法.误差维持图像加密算法打乱了块间置乱操作保留的对应关系,提高了加密图像的安全性.同时保留整体预测误差的分布,不会降低嵌入算法的性能.数据可逆嵌入阶段,利用图像的预测误差分布生成哈夫曼编码表用于自身标记压缩,相较于现有预先设定编码表或定长编码的方案具有更高的压缩性能,实现了更高的嵌入容量,以UCID图像库为例,平均嵌入率可达2.306 bpp.后续工作将从更高效的临界概率方案设计、图像加密算法安全性分析、算法时间复杂度优化等方面展开.