直升机飞行控制系统横侧向增稳控制律设计

刘彦涛

（陕西东方航空仪表有限责任公司，陕西西安，710100）

0 引言

对于线性系统而言，系统的极点决定系统的稳定性，影响系统的动态指标(超调量和超调时间)。因此，可以利用系统的可测状态（输出）反馈来配置相应闭环极点，使其落在满足品质规范要求的复平面区域内，并且距边界留出适当距离，这样即便受到扰动（如参数摄动，环境变化等）影响，系统也有相当的抵御能力，保证性能满足指标要求[1]。这一方法称为参数鲁棒设计法。

直升机自身稳定性差，气动特性随飞行高度、速度变化比较大，仅靠飞行员操纵来完成复杂、精确的飞行动作非常困难。故需要设计增稳控制律，借助于飞行控制系统，使直升机在飞行包线内满足飞行品质要求[2]。

文章中，直升机横侧向通道控制律设计要求是，在如图1所示飞行包线内选定的18个设计节点处，倾斜通道、航向通道均满足如下动态品质要求：

(1)倾斜通道：操作驾驶杆，使直升机产生±25º的倾斜角变化后松杆，直升机回到原平衡状态的调节时间ts≤ 5 s ，超调量 σ% ≤10%。

(2)航向通道：给定±5º的航向阶跃指令，直升机稳定在新航向上的调节时间ts≤ 5 s，超调量σ% ≤25%。

图1 飞行包线示意图

1 横侧向控制系统描述

直升机横侧向控制系统结构图如图2所示。

图2 直升机横侧向控制系统结构图

图2中的两个一阶环节分别是倾斜通道和航向通道助力器的传递函数。可以分别导出倾斜通道和航向通道助力器的微分方程：

将横向周期变距Aic、尾桨桨距δrc扩充为新的状态变量，可以导出扩充后直升机横侧向系统的状态方程。将可测量的4个状态作为输出可以得到相应系统闭环状态方程：

根据引言中对系统动态性能要求，可以分别确定倾斜、航向通道分别满足要求的系统闭环极点的分布范围为：

2 倾斜通道控制律设计

式(2)规定了满足要求的倾斜运动极点s1,2=−ξdωnd±的分布范围，这在s平面相应确定了一个扇形区域 ，如图3中灰色实线所描绘。设定合适的无阻尼自然频率上限ωmax=3rad/s 是受控制回路功率的限制，同时避免控制回路带宽过宽[3-4]。

暂不考虑ψg的影响，将问题化为倾斜通道ϕg单输入的情况来考虑。对倾斜通道进行参数鲁棒设计，确定控制参数kϕ,kϕ˙。

将式(1)在倾斜通道处于开环（没有ϕ,˙反馈）时的状态方程写出来，有：

将倾斜通道2个极点配置于图3扇形区域中某一位置，利用J.Ackermann定理[5],根据这一对极点可以确定相应的反馈参数向量Ka和另外5个闭环极点的位置。令这对极点沿着扇形区域的边界移动，就可以在控制参数空间(kϕ,kϕ˙)映射出相应的区域KΓ，如图4所示。这样就建立了控制参数与倾斜运动极点位置之间的映射关系，为进一步设计全包线控制律参数提供了有利的条件。

在选择Ka确定倾斜运动极点的同时，系统的另外五个极点并不受约束，在设计中应当注意使其限制在左半复平面，保证系统的稳定性和相关的要求。这样也就限制了倾斜运动极点在扇形区域中的一个子集，如图3中深色“×”所示的区域。

在飞行包线中所有18个设计节点均进行相应的参数映射，并将其可用的参数集合分别描绘在参数空间内，如果存在公共交集，则可以在其中适当选择参数，构成固定参数的控制器，使在包线范围内的倾斜动态响应均满足规定的要求。若不存在公共交集，则意味着达到控制要求的固定参数控制器原理上不存在，必须采用其他的控制方式（如调参控制等）才能达到设计要求。显然，各设计节点的可用参数集合在参数空间中的分布规律可以为合理确定调参规律提供参考信息。

18个前飞状态设计节点的倾斜通道可选参数集合分布情况显示，存在很小的可用公共参数交集，虽然可以在其中确定一个固定参数的控制器，但对有些节点而言性能并不满意，故选择调参控制方案，使系统的倾斜运动特性在包线内均具有满意的品质。

以节点12（飞行高度1000m、速度70m/s）的情况为例进行说明。在航向通道反馈联通（用标称参数而倾斜通道开环时，倾斜通道极点位于此时倾斜响应不稳定。配置倾 斜 通 道 极点于扇 形 区 域 内s1,2=−1.0728 ± j1.1149处（如图3中“△”所示），相应参数平面中的映射点为kϕ=0.6441,kϕ˙=−0.0823（如图4中 “△”所示，参数映射区域中深色“×”的部分是可用参数集合）。

图3 倾斜通道极点配置区域图

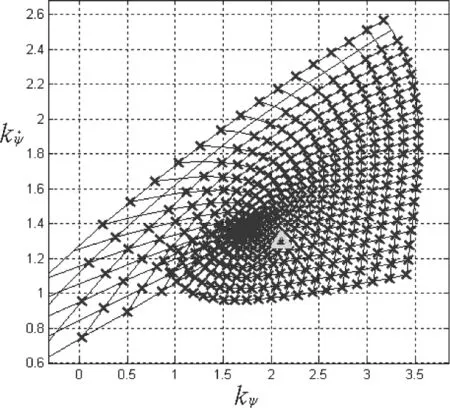
图4 倾斜通道控制参数映射区域图

分别对所有18个前飞节点进行映射，可以得到各节点倾斜通道控制参数在参数空间中的分布图，如图5所示。

图6显示了各设计节点倾斜控制参数k,k ϕϕ˙在包线中的分布规律，将其当作样本，通过拟合，可以得到全包线倾斜通道调参控制律。

图5 倾斜参数在参数平面的分布情况

图6 倾斜参数在包线中的分布规律

3 航向稳定控制律设计

与倾斜通道处理方法类似，倾斜通道控制参数取第2节中确定的kϕ、kϕ˙，将式(1)在航向通道处于开环时的状态方程写出来，调整状态向量顺序，将ψ、ψ˙ 提前，仅考虑

单输入的情形，有：

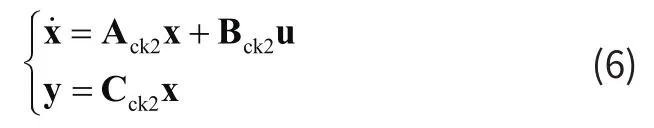
根据式(3)确定的设计要求，可以确定航向通道对应极点在s平面与动态指标相应的扇形区域，如图7所示。代入在第2节中设计好的倾斜通道控制参数k,k ϕϕ˙，倾斜通道反馈连通而航向通道开环时，航向开环极点位于-0.0048±j 1.8562，显然不在指标要求的扇形区域内。将航向通道极点配置在s1,2= - 1.3084 ± j 1.9725（如图7中“△”所示），在节点12条件下，相应参数平面中的映射点为kψ=2.1106,kψ˙=1.2935（如图8中“△”所示）。

图7 航向通道极点配置区域图

图8 航向通道控制参数映射区域图

分别对18个前飞设计节点进行映射，可以得到各节点航向通道控制参数k,k ψψ˙在包线中的分布规律如图9所示。将其作为样本，可以得到全包线航向通道调参控制律。

图9 航向控制参数在包线中的分布规律

4 仿真检验

在节点12条件下，给定初始倾斜角25度，在5度航向角阶跃输入时直升机的动态响应如图10所示。由图可以看出，系统倾斜角从25度回到稳态值的响应过程稳定，超调量为4.8%，调节时间2s；航向角从0度达到给定值5度的调节时间未2.6s，超调量10%[6]。满足给定的设计要求。

5 结论

本文运用参数鲁棒设计方法设计了直升机横侧向控制系统的增稳控制律参数。分别根据给定的横侧向通道动态指标要求进行参数空间映射，确定控制参数的可用集合；选定所配置极点对应的各节点的控制参数作为包线内的调参样本，确定包线内的调参控制律。在此过程中，设计者可以根据具体情况在可用参数集合中进行设计，保证系统的稳定性和希望的动态品质。

图10 ψ g=5° ，ϕ(0)=25°时的动态响应曲线