MEMS陀螺仪的稀疏冗余去噪∗

杨金显韩玉鑫(河南理工大学电气工程与自动化学院导航制导实验室,河南 焦作454000)

MEMS陀螺仪以其成本低、体积小、数据输出率高等优点,广泛应用于航空航天、随钻测量等领域[1]。由于制造工艺的限制,MEMS陀螺仪相比与传统陀螺仪精度较低。在钻头钻进复杂地质环境的过程中,受到振动的强烈程度不一、温度效应及其他随机扰动的影响,导致采集的陀螺仪信号呈现多频及非线性特征[2],难以补偿。因此,MEMS陀螺仪的误差补偿技术显得尤为重要。

目前,陀螺仪信号的去噪可大致分为建模和非建模的方式。建模方法[3－5]降噪是在随机噪声时间序列的基础上建立自回归滑动平均模型,然后利用卡尔曼滤波对模型的输出进行实时更新。由于卡尔曼滤波需要相对完整的信号和噪声统计特性,因此其初始参数的确定较为复杂,存在收敛速度慢、初始过渡状态长等问题。非建模方法[6－8]降噪包括数字低通滤波器、小波变换和EMD等方法。数字低通滤波器可以消除高频噪声,但当信号频带与噪声频带相近时,滤波效果较差。小波变换需要选择分解层次和小波基,分解参数的选择,分解结果会受到信号特性的影响。EMD方法克服了小波变换固定基函数的缺点,可有效提取非平稳、非线性信号的瞬时特征参数和Hilbert谱,从而精准分析信号特征[9]。Gu,HY等人[10]采用改进的全集成经验模态分解方法将原始信号分解为一系列固有模态函数,并通过阈值对固有模态函数进行滤波；通过bagging极限学习机器的模型训练去噪后的子序列重构的训练数据集和测试数据集,利用测试数据集对补偿信号进行预测。然而该方法需要大量的数据集,且神经网络存在收敛速度慢,易陷入局部极小点的问题。Wu YC等人[11]提出组合广义形态滤波器的自适应多尺度方法对陀螺仪输出信号去噪,在变分模分解将原始信号分解为多尺度模的前提下,利用自适应多尺度对结构单元进行选定,有效降低不同模态对应的噪声。应用以EMD为基础的智能算法及在EMD基础上改进的算法,可有效提高信号的质量,但不能体现处理信号的实时性,且高频的模态分量含有大量的噪声,低频部分体现陀螺仪信号的主要特征。

压缩感知[12－13]理论可以利用信号的稀疏性或在其他变换域上的稀疏性,通过不等间距采样优化逼近真实信号。文献[14－15]都针对陀螺仪信号进行小波分解后小波系数的筛选问题,利用CS算法,转化为小波系数稀疏性的恢复问题,通过对比不同的稀疏重构算法,证明了CS方法对陀螺仪信号处理的有效性。Song,JL等人[16]更是应用小波分析的方法消除MEMS陀螺仪信号中的噪声,采用稀疏冗余的方法优化小波系数,通过滞后校正的方法降低小波分解的边界效应。应用CS算法对小波系数处理需要构建稀疏提取的构架及挑选最稀疏的分解系数,其次正交匹配追踪或自适应匹配追踪的重构算法需求较多的训练样本。

针对以上分析,提出了EMD算法对陀螺仪信号进行分解,利用两个连续重构陀螺仪信号的欧氏距离对高频IMFs分量和低频IMFs分量进行分离,剔除高频噪声IMFs分量对陀螺仪测量精度的影响。利用CS理论对剩余IMFs稀疏优化,通过对陀螺仪误差补偿项的估计,叠加重构优化后的剩余IMFs和误差补偿项,从而提高MEMS陀螺仪的测量精度。

1 EMD分解及指标参数的确定

1.1 EMD分解

通过利用陀螺仪信号局部特征的时间尺度,将其分解为一系列从高频到低频的振荡IMF分量。含噪的陀螺仪信号x(t)分解出L个IMF,即模态函数分量hi(t)(1≤i≤L)和余项rL(t)。由此,陀螺仪的重构信号可表示为:

通常,在EMD分解陀螺仪信号的模态分量中,低频部分反映信号的主要特征,噪声主要集中在高频部分,剔除高频噪声分量的干扰,重构剩余分量即可得到去噪后的陀螺仪信号。在多种因素的扰动下,漂移误差的存在,需补偿陀螺仪误差减小对MIMU测量系统的影响。根据以上分析,含噪的陀螺仪信号可表示为:

式中:C为陀螺仪信号中高、低频IMFs分量的分界点的指标参数,～hi(t)为陀螺仪高频IMFs噪声分量,hi(t)为陀螺仪低频IMFs信息分量,w(t)为陀螺仪信号的误差补偿项。

1.2 指标参数C的确定

MEMS陀螺仪在高温强振等复杂的工作环境下,其测量精度受到较大的影响,原始信号和噪声是未知的,因此无法完全去除陀螺仪信号中的噪声部分。在实际应用中,陀螺仪信号的高频噪声分量和低频信息分量难以区分,无法通过绝对误差或均方误差实现分离,文献[17]提出了连续均方误差(CMSE)的方法,有效计算MEMS陀螺仪高频信号和低频信号分界点的指标参数。对陀螺仪信号分解的模态分量重构如下:

利用CMSE计算两个连续MEMS陀螺仪重构信号之间欧氏距离的平方,具体如下:

由于MEMS陀螺仪的噪声主要集中在高频部分,随着EMD的不断分解,噪声的能量逐渐降低。因此,将高频IMFs与低频IMFs的能量分界点定在IMFs能量的第一个最小值处。由此陀螺仪信号的高、低频模态分量指标参数为:

式中:k的取值范围为1≤k≤2D/3,当MEMS陀螺信号的转动速度达到恒速时,k取最大值2D/3。根据以上分析,可认为两个连续的陀螺仪重构信号之间的欧氏距离平方越小,两个信号之间的差值越小,对应的hk(t)能量越低。因此,可使用CMSE方法来识别高、低频分量指标参数。

2 稀疏重构及误差补偿估计

稀疏表示的基本思想是在构建信号的测量矩阵的基础上进行表示,并求解其系数矢量。根据测量矩阵中的非零元素,可对EMD分解得到的模态分量中的主要特征进行分析。

2.1 稀疏表示

首先利用CS对剩余IMFs分量进行稀疏表示,陀螺仪的重构信号可表示为:

式中:hi(t)为陀螺仪实际观测值,s(t)为真实信号,n(t)为高斯白噪声。设H为陀螺仪测量信号hi(t)在给定尺度上大小为N×1的稀疏系数列向量,由CS理论可知,存在增广测量矩阵ΦM×(N＋1),其中测量矩阵为ΦM×N(M≤N),矩阵ΦM×1为陀螺仪误差补偿矩阵,此时存在观测向量y,使得:

式中:观测向量y在给定尺度上的大小为M×1的列向量。由于y的维数远低于H的维数,方程难以求解。真实剩余IMFs分量的稀疏系数H在t上稀疏的。在ΦM×N满足约束等距的情况下[14],对于常数δt∈(0,1)有:

式中:‖·‖2表示向量的模值,即l2范数,稀疏系数可由测量值y求解最优范数。

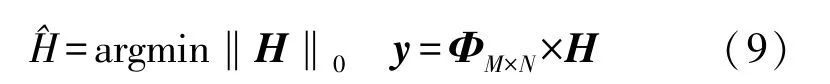
式中:‖·‖0表示向量l0的范数,即非零元素的个数,测量矩阵ΦM×N选择高斯矩阵；测量向量y的维数M满足M≥Klog(N)。

2.2 贝叶斯重构

基于贝叶斯统计原理,通过对剩余IMFs分量的最大后验点的均值估计来重构信号。根据支持向量机理论,利用分层的先验模型求出剩余IMFs分量的均值和方差,从而求得剩余IMFs的真实值。

根据贝叶斯理论,在求解yi的密度函数下,采用Laplace概率分布对hi(t)建模如下:

然而,当直接采用Laplace密度函数难以求解hi(t)先验时,可以用高斯密度函数精度β(β1,β2,…,βn)分量的乘积表示陀螺仪误差补偿项w(t)的先验分布:

β服从个Gamma分布且,对得到的后验分布进行参数β和β0的最大后验估计,由Bayes定理可得:

通过相关向量机模型可得hi(t)均值和方差估计:

式中:Λ＝diag(β1,β2,…,βn),代表对角矩阵。通过求解β和β0的最大边缘分布,可得β和β0的更新表达式:

式中:μi,j为第j个后验均值矢量；Σi,(j,j)为Σi对角线上的元素；β和β0的上标表示迭代更新的值。通过对式(14)～(17)的联合迭代得到陀螺仪信号hi(t)的最大后验估计。

2.3 误差补偿项估计

根据增广矩阵中的误差补偿矩阵ΦM×1,陀螺仪的误差估计值可表示为:

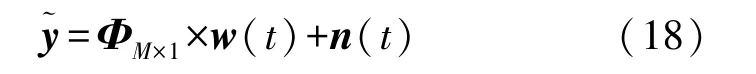
同理,根据2.2节,可通过贝叶斯估计求解出陀螺仪误差补偿项w(t)的值。

通过对MEMS陀螺仪信号进行EMD分解,利用CMSE算法界限高低频模态分量,在剔除高频噪声模态的前提下,对剩余IMFs分量稀疏冗余优化,采用贝叶斯估计补偿陀螺仪误差。综上,基于稀疏表示的EMD对MEMS陀螺仪降噪的算法流程如图1所示。

图1 稀疏冗余算法流程

3 实验分析

3.1 实验方案

为了检验稀疏冗余算法对MEMS陀螺仪的降噪性能,设计了转台实验和实际钻进实验。首先,在转台实验中,设计了静态和动态两种状态,可以验证陀螺仪在不同状态下的去噪效果。然后,通过模拟钻进实验,优化后的陀螺仪数据解算出的方位角的显著改善,证明该算法的有效性。最后,设置以下三种实验方案。

方案一:MEMS陀螺仪的原始输出信号；

方案二:采用EMD算法；

方案三:采用EMD-CS算法。

通过使用均方误差RMSE和信噪比SNR来比较以上三种方案的降噪效果。RMSE可表示为:

式中:x(t)为陀螺仪真实信号,N为陀螺仪数据采集总数,y(t)为降噪后的信号值。

3.2 转台实验

本次实验数据是通过设计的无线蓝牙MIMU系统采集。MIMU系统模块的陀螺仪参数为:0.005的噪声密度,18°/hr的稳定性偏差。通过调制转台速率收集数据:①将MIMU系统模块水平固定在转台上,如图2所示；②接通电源进行预热；③静置200 s,记录静态下陀螺仪的数据,之后给转台使能,使其达到10°/s的转速,采样间隔0.02 s,连续采样10000点,记录采集数据。

图2 MIMU转台实验

首先对含噪的MEMS陀螺仪数据进行EMD分解,其分解得到9个模态分量和1个余项,如图3所示。通过CMSE计算参数C的值,当C＝6时,所得到的两个重构陀螺仪信号间的欧式距离平方最小,因此可将IMF1－IMF5的高频噪声模态分量剔除。通过对剩余IMFs分量进行稀疏冗余处理,图4为对剩余IMFs分量优化前后的效果,明显可以稀疏提取信号特征。

图3 陀螺仪信号的EMD分解

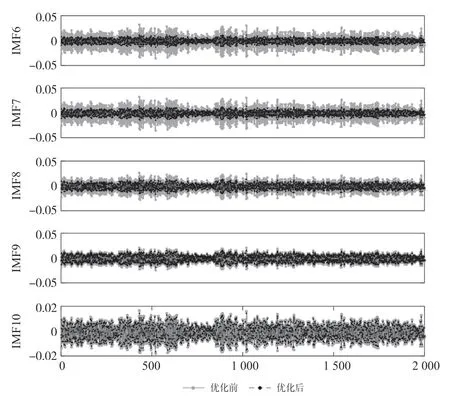
图4 剩余IMFs分量稀疏冗余优化前后

表1为3种方案的RMSE和SNR的计算结果,图5(a)、(b)分别为陀螺仪在静态、10°/s转速下的去噪效果,从表1和图5可以看出,基于EMD的稀疏提取对陀螺仪的降噪有明显效果,SNR值相对于原始信号及EMD算法分别提高了27.5%、12.6%,RMSE值分别降低了82.9%、61.8%。

图5 3种方案对陀螺仪信号降噪后的对比

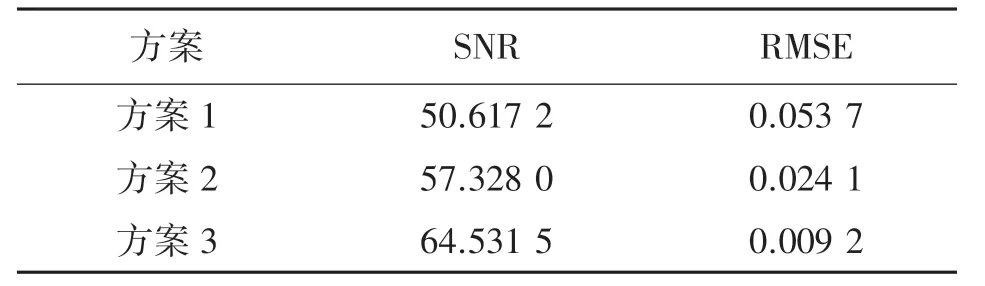
表1 三种方案的SNR和RMSE比较

为进一步的验证3种方案的降噪效果,设置转台转速为100°/s,收集数据。对优化后的陀螺仪信息进行姿态解算,结果如图6所示。陀螺仪在短的时间内,解算得到的方位角误差较小,随着时间的加长,其累计误差在不断加大。方案2的累积误差由0.5852°减小到0.4507°；方案3的方位角累计误差由0.5852°减小到0.2375°。

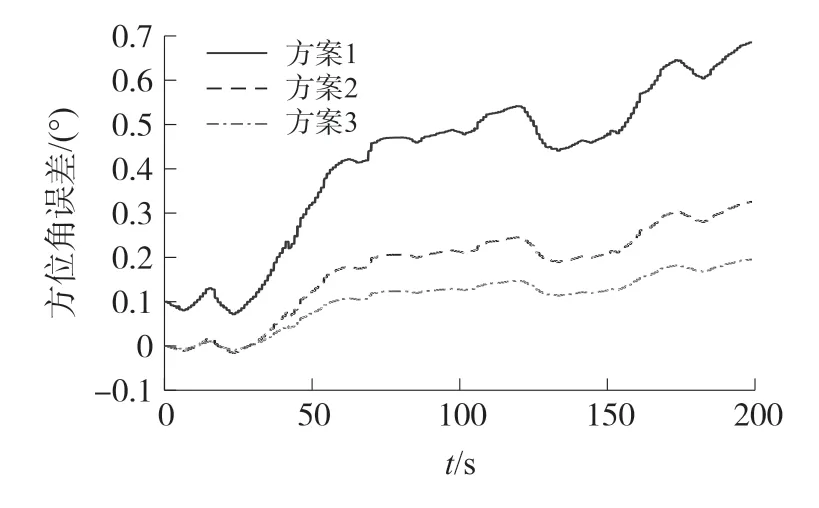
图6 转速100°/s时方位角解算误差对比

3.3 钻进模拟实验

为了更好的验证稀疏冗余算法对MEMS陀螺仪去噪的优良性,设计了模拟钻进实验,通过将装有蓝牙功能的MIMU模块固定在钻杆根部,如图7所示。在进行钻进前,首先将钻机的倾斜角调整为45°,钻进中,以转速为360°/s恒定钻压垂直钻进,为了减少随时间加长漂移误差较大的影响,每间隔100 s停钻一次,整个钻进过程每间隔1 s采集陀螺仪数据；然后以初始倾斜角直行钻进,钻机在稳定时有特定的转速,当钻进不同材质时,其振动的幅值在变化,模拟钻进的三轴陀螺仪信号及优化后的效果如图9所示。由此可以看出,方案三可以较好的处理振动等因素下的陀螺仪噪声。

图7 模拟实钻实验

通过对模拟钻进的陀螺仪数据进行方位角解算,结果如图8所示。在基于EMD处理下,累积误差由11.8562°减小到0.5637°。而基于EMD稀疏冗余的优化下,方位角累计误差由11.8562°减小到0.4725°。

图8 模拟钻进的方位角解算误差对比

图9 不同方案对钻进实验下三轴陀螺仪信号的处理

4 结论

通过对含噪MEMS陀螺仪信号的分析,利用EMD算法的自适应性及连续均方误差对高低频模态分量的识别,有效去除高频噪声模态分量的影响。构建冗余字典,使剩余IMFs分量在该字典上稀疏优化。同时,增添误差补偿列使构成新的增广矩阵,利用贝叶斯估计补偿项。通过转台和模拟钻进实验,证明陀螺仪信号在基于EMD的稀疏表示下要优于EMD算法；对优化后的陀螺仪信息进行姿态解算,其方位角的累积误差由11.8562°减小到0.4725°,进一步验证了该方法可以有效提高MEMS陀螺仪的测量精度。