考虑降雨和库水位联合作用的边坡稳定性分析

刘小毛

（吉安市水利水电规划设计院，江西吉安343000）

我国地质条件非常复杂，边坡失稳是主要的地质灾害之一，其中库区边坡由于受到库水位升降的影响，使岩土体材料发生劣化常产生垮塌，但降雨作用对边坡稳定性的影响也是不可忽略的[1-3]。降雨和库水位联合作用使土体有效应力减小，土体内部基质吸力也减小，同时土体相关强度参数也降低，从而使库区边坡垮塌问题成为最具威胁的自然灾害之一[4-6]，因此有必要对两者同时作用下的边坡稳定性规律进行详细地研究，从而对库区边坡的防治提供指导。

1 模型建立

1.1 网格划分

计算采用大型通用有限元软件MidasGTS，该软件是针对岩土领域研发的通用有限元软件，不仅支持线性/非线性静力分析、渗流和固结分析，也在边坡稳定性分析中常被用到。

所研究的库岸边坡正常蓄水位取115m，死水位取105m，该边坡较为平缓，下部为基岩，上部依次为卵砾石、碎石夹黏土和黏土覆盖层。网格采用四边形网格划分，在模型建立时对一些弧线进行多段线简化处理，然后将简化线框导入MidasGTS进行模型建立。根据不同工况的水位情况赋予岩土体材料不同的参数，水位线上采用天然容重、天然黏聚力、天然内摩擦角，水位线下采用浮容重、饱和黏聚力、饱和内摩擦角。网格划分时将基岩边界尺寸控制在4～5m，而关键区域（覆盖土层）的网格尺寸控制在1～2m。

1.2 边界条件

对模型底部约束X，Y2个方向的位移，对模型左、右两侧约束X方向位移。模型底部为不透水边界，水位在105～115m之间变动，入渗强度的大小由降雨强度和渗透系数两者大小关系决定：若渗透系数大于降雨强度，则入渗强度取降雨强度大小；若渗透系数小于降雨强度，则入渗强度取渗透系数。在计算时认为边坡表面无积水。

1.3 计算工况

计算工况主要考虑3种：1）仅考虑库水位下降对边坡稳定性的影响；2）库水位固定仅考虑不同降雨类型对边坡稳定性影响；3）考虑不同降雨时长的边坡稳定性影响，具体计算工况如表1所示。降雨类型主要分为4种：平均型（a）、前锋型（b）、中锋型（c）和后锋型（d）降雨[7]，降雨时程曲线如图1所示。

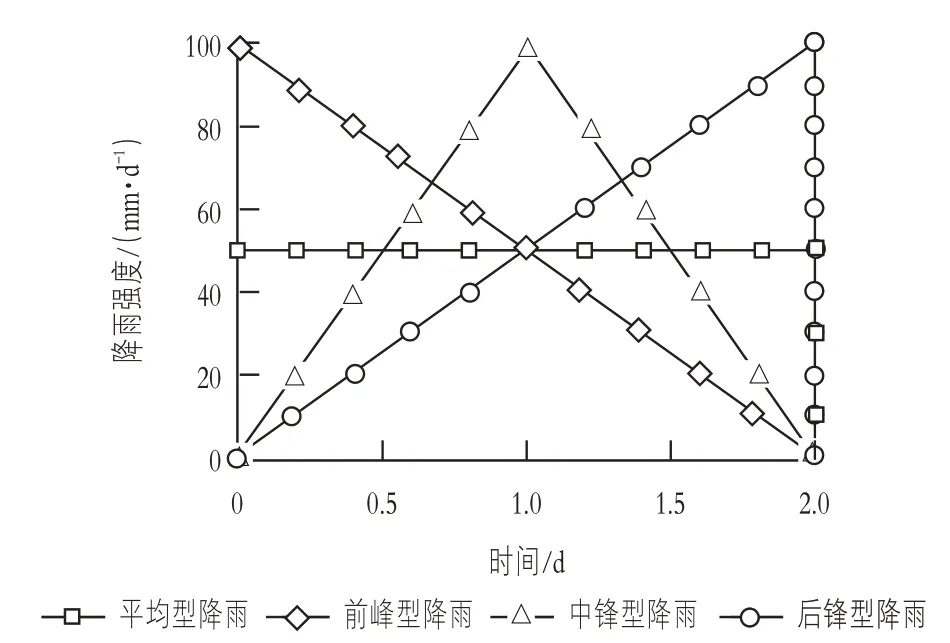
图1 不同降雨类型时程曲线

表1 计算工况

2 结果分析

2.1 工况1

工况1仅考虑库水位下降的影响，分别设置了3种下降速度，根据监测数据得到的孔压变化规律如图2（a）所示。不同库水位下降速度下的孔压变化规律整体大致相同，均随着时长增加而缓慢降低，并最终趋于稳定，均稳定在-10kPa左右；但不同库水位下降速率下的孔压变化略有差异，库水位下降速度越大，在初期孔压下降速率越大，越早进入孔压稳定阶段。稳定性系数变化规律如图2（b）所示，不同库水位下降速度下的稳定系数均呈现先减小后增大的趋势，不同库水位下降速度均存在一个最小稳定性系数，且库水位下降速度越大，最小稳定性系数越小。

2.2 工况2

图2 工况1计算结果

孔压变化规律如图3（a）所示，不同降雨类型下孔压均呈现先增加后减小的变化趋势，平均型降雨下的孔压相较于其他3种降雨类型对应的孔压低一些，前锋型降雨类型对应的孔压相对最高。稳定性系数变化规律如图3（b）所示。4种降雨类型影响下的边坡稳定性系数均呈现先急剧减小后缓慢增大的趋势，说明在降雨条件下，边坡在最初一段时间稳定性会急剧降低并在停止降雨后的某个时间点会达到最不稳定状态，但随后稳定性又会逐渐增加。4种降雨类型对边坡稳定性影响顺序依次为后锋型降雨、平均型降雨、中锋型降雨和前锋型降雨。

2.3 工况3

对于工况3,仅计算了其稳定性系数变化规律。如图4所示，不同降雨时长下稳定系数随着时间变化规律是相同的，均呈现先减小后增大最终趋于稳定的趋势，不同降雨时长条件下均存在一个最小的稳定性系数。原因是降雨初期随着降雨入渗边坡内部坡体内部水分来不及排出，孔隙水压力增加有效应力减小，但随着时间增加，内部水分逐渐入渗并排出边坡内部，所以稳定性系数又逐渐增加。不同降雨时长下的稳定性系数变化规律略有差异，明显降雨时间越长边坡稳定性系数减小幅度越大。

图3 工况2计算结果

图4 稳定性系数变化规律

3 结论

1）对于仅考虑库水位骤降情况，不同库水位下降速度下的孔压变化规律整体大致相同，均随着时长增加而缓慢降低，并最终趋于稳定，均稳定在-10kPa左右；不同库水位下降速度下的稳定系数均呈现先减小后增大的趋势。

2）不同降雨类型下孔压均呈现先增加后减小的变化趋势，平均型降雨下的孔压相较于其他3种降雨类型对应的孔压低一些，前锋型降雨类型对应的孔压相对最高；4种降雨类型对边坡稳定性影响顺序依次为后锋型降雨、平均型降雨、中锋型降雨和前锋型降雨。

3）不同降雨时长下稳定系数随着时间变化规律是相同的，均呈现先减小后增大最终趋于稳定的趋势，不同降雨时长下的稳定性系数变化规律略有差异，明显降雨时间越长边坡稳定性系数减小幅度越大。