基于物理模型的中小河流河道堤防工程地质参数试验分析

孙彦彪

(辽宁瑞宸工程建设监理咨询有限公司，辽宁 铁岭 112003)

0 前 言

当前，中小河流管理需要合理设置河堤工程地质参数，以提高中小河流在施工过程中的稳定性[1]。传统方法主要使用数值模型仿真来计算工程地质参数[2]-[6]。该方法的优点在于，它可以为各种河流堤提供更精确的地质参数时空分布，但是操作起来更加复杂。需要建立河堤的数学模型[7]。近年来，许多区域已经使用物理模型测试了河堤的地质参数分析。这种方法的优点是它更适合实际工程项目，但缺点是需要更多的资金来完成[8]。近年来，通过野外观察实验确定河堤地质参数。这种方法比较容易，基本上可以满足中小型河道工程的实际需要。它是通过测量许多地区河堤建设的地质参数而获得的[9-14]。由于尚未应用到辽宁地区，因此结合物理模型和现场观测来分析和优化辽宁地区中小河堤防工程的地质参数。研究结果对于确定中小型河流堤防工程治理和设计具有参考意义。

1 地质参数分析方法

物理模型水流流体，设定为多孔传输的介质，河道堤防的渗透系数采用达西定律进行计算：

(1)

该渗透系数物理模型简化了传统统达西计算定律的计算方程：

(2)

式中：K为确定的河道堤防渗透系数，cm/s；J为水力学比降，%；h为计算水头，cm；S为水力半径，cm；r为容重值，kg/m3。渗透孔隙度计算方程为：

(3)

由方程：

(4)

水流阻力系数计算方程为：

(5)

式中：a和u分别为地质参数。非稳定渗透水流的计算方程为：

(6)

各方向渗透系数的参数为常数值，则方程可简化为：

(7)

若按照同一个方向进行渗透，则方程为：

(8)

式中：Z为渗透水流计算参数值。

2 研究实例

2.1 物理模型概况

物理模型试验由过度连接段、动床河段、稳水河段三个部分组成，总长为45m。验河槽动水段和过渡连接河段分别为30m和5m，采用长度为20cm的粗砂段将过渡连接河段与动水河床段进行连接，物理模型试验河段如图1所示。

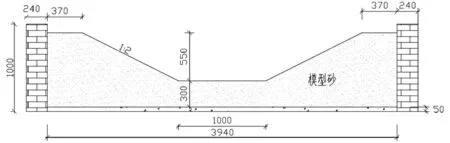
图1 模式试验河段平面布置图

2.2 地质参数分析

采用物理模型放水试验的方式对地质参数进行确定，首先结合原位观测试验方式对中小河流堤防施工不同试验断面的地质参数进行分析，如表1所示，结合各试验河段的地质参数，分别进行15组物理模型方式试验，对其稳渗参数进行确地，渗透系数确定结果如表2所示。

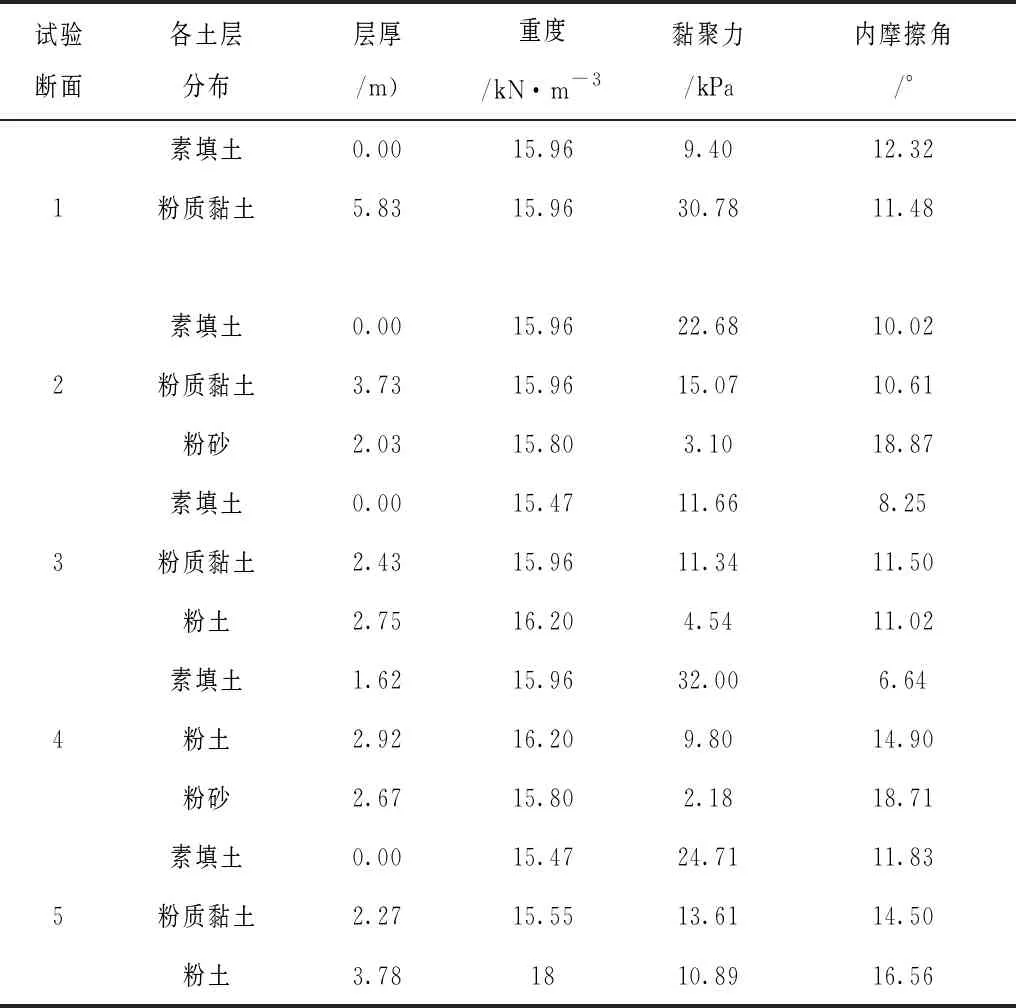
表1 各试验河段地质参数

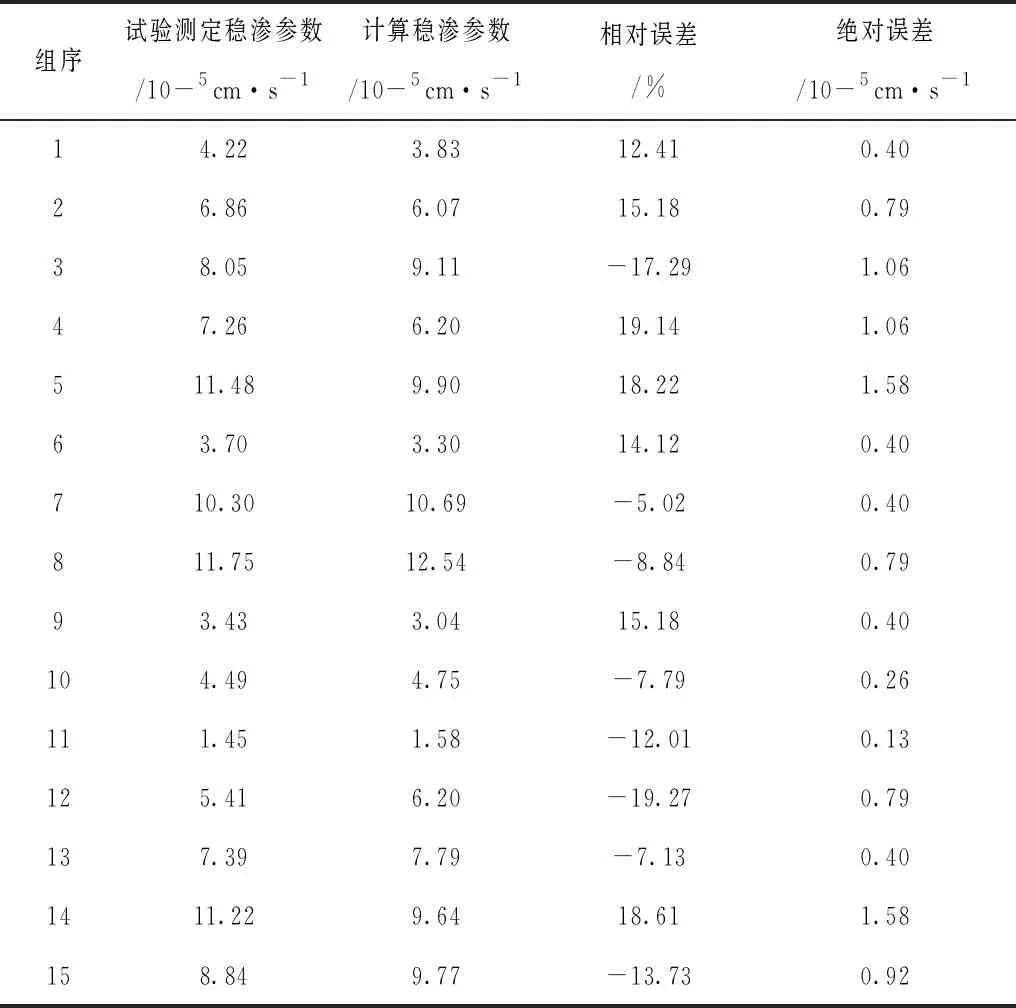
表2 地质稳渗系数分析结果

从试验分析结果可看出，不同河段地质参数具有较为明显的差异度，河道堤防地质参数受不同土层类型影响较大，此外各地质参数随着土层厚度的增加，对于同一类型土层而言，其地质各项参数具有所递增。对于相同土层厚度而言，粉质黏土的黏聚力在中小河流堤防工程土层中最大，其次为素填土。而对于内摩擦角而言，粉砂由于具有较低的黏聚力，使得其内摩擦角较大，而对于河道堤防工程而言，内摩擦角越大，越不利于河道堤防工程的稳定性。由于具有较高的黏聚力，素填土的内摩擦角较大，有利于河道堤防工程的稳定性。文章重点对河道堤防工程地质稳渗系数进行了分析，从稳渗分析结果可看出，试验测定的稳渗系数和计算的稳渗系数之间的误差较低，可满足河道堤防工程设计的要求。一般而言，对于稳定系数较高的河道堤防试验段其误差相对较低，而对于稳定系数较低的河道堤防试验段其误差一般相对较高。

2.3 不同方法对比分析

结合15组放水试验测定稳渗系数进行分析，分别对传统方法和新方法下的稳渗系数进行对比分析，从而确定较为优化的河道堤防施工地质参数的方法，两种方法对比结果如表3所示。

表3 两种方法的稳渗系数对比结果

稳渗系数是中小河流堤防治理工程重要的一项地质参数，其对于河道堤防工程的稳定性十分重要。近些年来，对于稳定系数的获取主要通过原位观测试验的方式进行，但这种方式很难得到不同地质类型下的稳定渗透系数，存在一定的局限性，为此文章采用物理模型并结合原位观测两种方式，提高了不同地质类型对其稳定系数的科学核定。从两种方法计算的稳定渗透系数的精度结果可看出，相比于传统只采用原位观测试验的方式，通过物理模型试验方式可以实现不同河道堤防地质类型以及放水流量对其河道堤防稳定渗透系数的影响，且新方法下计算的稳定渗透系数的精度也明显要好于传统方法，采用新方法计算的稳定渗透系数的误差均可在20%以内，相比于传统稳定渗透系数的计算方法，且相对误差可以降低5.6%左右，精度提升效果较为明显。

3 结 论

1)对于同一类型土层而言，其地质各项参数具有所递增。对于相同土层厚度而言，粉质黏土的黏聚力在中小河流堤防工程土层中最大，其次为素填土。而对于内摩擦角而言，粉砂由于具有较低的黏聚力，使得其内摩擦角较大，而对于河道堤防工程而言，内摩擦角越大，越不利于河道堤防工程的稳定性。

2)稳渗系数是中小河流堤防治理工程重要的一项地质参数,一般而言，对于稳定系数较高的河道堤防试验段其误差相对较低，而对于稳定系数较低的河道堤防试验段其误差一般相对较高。

3)采用新方法计算的稳定渗透系数的误差均可在20%以内，相比于传统稳定渗透系数的计算方法，且相对误差可以降低5.6%左右，精度提升效果较为明显。