考虑路段突发性堵塞的旅行商问题与算法*

孙璐璐，苏 兵，邵 郁，姬 浩，张 萌

(1.西安工业大学 经济管理学院，西安 710021；2.西安交通大学 管理学院，西安 710049)

经典旅行商问题(Traveling Salesman Problem，TSP)指在交通网络中路段权值(一般指长度/通行时间等)确定的情形下旅行者从起点出发且经过每个中间节点只一次最后回到起点的最短路径选择问题[1]。有研究对经典TSP问题的求解算法进行改进[2-4]，有研究考虑包含优先级约束的TSP问题[5]，包含随机客户的选择性TSP问题[6]，环形路网上以总服务时间尽可能短为目标的在线TSP问题[7]，带有线性惩罚的在线TSP问题[8]，有服务时长和服务可选择性的在线TSP问题[9]等。实际交通网络中路段经常发生堵塞，现有TSP问题的相关研究均未考虑路段发生堵塞的情形。旅行者一旦遭遇突发性堵塞，在不考虑堵塞情形下所选择的旅行路径就会失效，并且带来时间损失；已有研究考虑路段突发性堵塞的路径选择主要为替代路径[10]、绕行路径[11-12]、最优安全路径[13-14]和最优抗风险路径[15-16]等，均未考虑TSP问题的特点，即要求路径必经中间节点，无法满足实际需求。

本文针对考虑路段突发性堵塞的TSP问题，基于交通网络中任意路段均可能发生堵塞的情形，在旅行者出发前选择一条从起点出发且经过所有必经中间节点后到达终点的抗堵塞路径，使得遭遇突发性堵塞所带来的时间损失尽可能小。文中提出路段堵塞所带来时间损失的度量指标：路段堵塞损失值，建立最优抗堵塞旅行路径选择模型并设计算法求解，为旅行者出发前的路径选择提供决策依据。

1 问题描述及相关定义

2 最优抗堵塞旅行路径选择模型

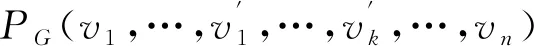
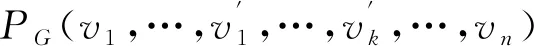
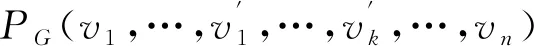
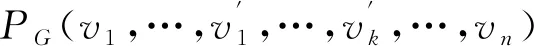
根据定义1，提出路段堵塞所带来时间损失的度量指标：路段堵塞损失值，有定义2。

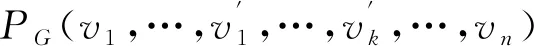
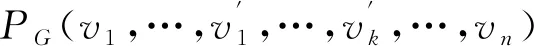
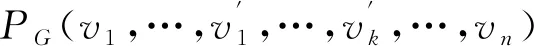
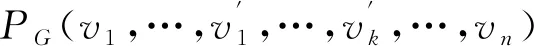
网络中存在多条从v1出发且经过V′中所有节点后到达vn的路径，每条路径均可计算其抗堵塞关键路段；比较所有抗堵塞关键路段的路段堵塞损失值，可得出最小路段堵塞损失值；包含最小路段堵塞损失值所对应路段的路径称为抗堵塞旅行路径，有定义4。

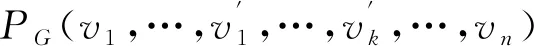
网络中可能存在多条抗堵塞旅行路径，因而称通行时间最短的抗堵塞旅行路径为最优抗堵塞旅行路径，有定义5。

3 最优抗堵塞旅行路径的求解

求解最优抗堵塞旅行路径可以通过计算出网络中的每条满足条件的旅行路径，比较每条路径的抗堵塞关键路段的堵塞损失值大小，并结合路径自身的通行时间求出最优抗堵塞旅行路径；但是该方法的时间复杂度很高。通过分析最优抗堵塞旅行路径选择模型可以看出，求解最优抗堵塞旅行路径的关键是求出抗堵塞关键路段。通过分析网络中路段的性质，排除不可能成为抗堵塞关键路段的路段，可以有效降低算法的时间复杂性。

通过观察和分析，发现网络中存在一类特殊路段，此类路段的通行时间大于其两个端点间最短路径的通行时间。一旦旅行者到达这类路段的起始节点时遭遇堵塞，可选择路段的两个端点之间的最短路径进行绕行，使得路段堵塞损失值第2部分L″的值为0。称这类路段为最大后悔路段，有定义6。

定义6 最大后悔路段。对于某路段eab，如果其通行时间严格大于两个端点之间的最短路径通行时间，即tab>TG(va,vb|SP)，则称这条路段为最大后悔路段Leab。

由定义6可知，与最大后悔路段的路段堵塞损失值相关的仅有起点v1到该路段起始节点之间的路径，因此最大后悔路段在该路径上越靠近终点，其路段堵塞损失值就越大。给出如下定理1，即最大后悔路段的特殊性质。

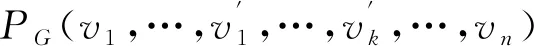
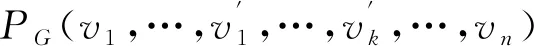
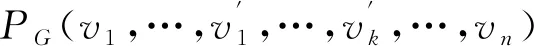
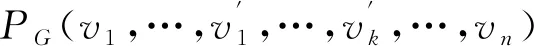
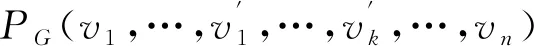
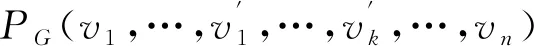
由情形1可知Lab=0，对于en-1,n，由于其非最大后悔路段，故其绕行路径的通行时间大于G中从vn-1到vn的最短路径通行时间，所以有Ln-1,n>0。

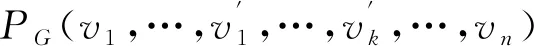
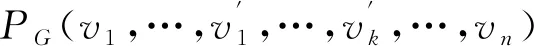
由定理1可以得出推论1。

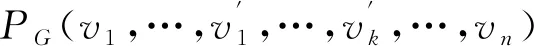
通过对交通网络中特殊路段分析可知，最大后悔路段非抗堵塞关键路段，因此抗堵塞关键路段存在于以vn为根的最短路径树上。在设计算法时，由于要求旅行者经过k个必经中间节点，则计算最短路径树时不能将起点、k个必经中间节点、终点很好地连结在一起，除非k个必经中间节点恰好位于在从起点到终点的最短路径上。鉴于此，需要求出从起点经过k个必经中间节点到达终点的最短路径，并从最短路径上的路段出发逐步计算出最优抗堵塞旅行路径。

最优抗堵塞旅行路径的算法A思想为：计算从起点经过k个必经中间节点后到达终点的最短路径及其抗堵塞关键路段，将交通网络中的最大后悔路段从最优解排除。删除这条抗堵塞关键路段，在剩余的交通网络中依次计算最短路径及抗堵塞关键路段，并和前一次计算所得结果比较堵塞损失值，若后者不小于前者，则算法结束；若后者小于前者，则删除抗堵塞关键路段并继续迭代，直到满足后者不小于前者为止。此时交通网络中的最短路径即为最优抗堵塞旅行路径。

计算最优抗堵塞旅行路径的算法A步骤为

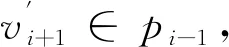
3) 输出pk-1；

5)令P1=dist(v1,V1)+pk-1+dist(vn,Vn)，j=2tok-1：

Pj=dist(v1,Vj)+pk-1-dist(Vj-1,Vj)+dist(pn-1(first),pn-1(last))+dist(Vj-1+vn)；

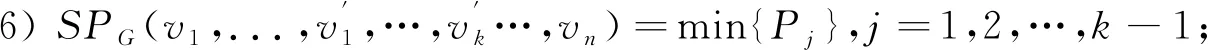
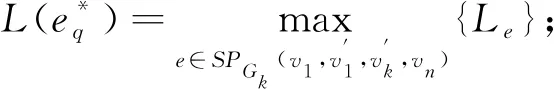
τ=q-1，否则转入10)；

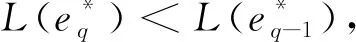
定理2在n个节点和m条路段的无向网络上，从起点v1经过k个必经中间节点到终点vn的最优抗堵塞旅行路径可在O(kn3)时间内输出。

4 实例分析

实例1和2均为合肥市的局部路网，其中实例1包含单个必经中间节点，实例2包含多个必经中间节点。

1) 实例1 为单个必经中间节点服务

合肥市局部路网和抽象图如图1和图2所示。图2中各条路段的权值表示图1中相应路段的通行时间，且任意一条路段均可能发生堵塞；标出的节点为必经中间节点。现需选择一条抗堵塞路径，起点为肥东新周谷堆农产品市场v1，必须经过网络中的餐馆v10并为其配送农产品，最后前往位于长江东路与铜陵路交叉口的终点v16，目标是为运输车辆(即旅行者)在出发前选择一条抗堵塞路径。

图1 合肥市局部路网(为单个必经中间节点服务)

图2 合肥市局部路网抽象图(为单个必经中间节点服务)

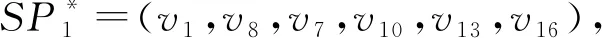
2) 实例2 为多个必经中间节点服务

合肥市局部路网和抽象图如图3和图4所示。图4中各条路段的权值表示图3中相应路段的通行时间，且任意一条路段均可能发生堵塞；标出的节点为必经中间节点。现需选择一条抗堵塞路径，起点为肥东新周谷堆农产品市场v1，必须经过网络中的v5、v7、v10和v15这4个餐馆并为其配送农产品，最后前往位于长江东路与铜陵路交叉口的终点v16，目标是为运输车辆(即旅行者)在出发前选择一条抗堵塞路径。

图3 合肥市局部路网(为多个必经中间节点服务)

图4 合肥市局部路网抽象图(为多个必经中间节点服务)

5 结 语

研究发现旅行者从起点出发为必经中间节点服务后到达终点的过程中，经常会遭遇突发性堵塞，由于堵塞发生的位置具有不可预知性且会导致路段无法通行，会给旅行者带来时间损失。在旅行者出发前选择一条从起点出发且经过所有必经中间节点后到达终点的抗堵塞路径，使得路段突发性堵塞所带来时间损失尽可能小，具有重要的意义。研究结果针对交通网络中任意路段均可能发生堵塞的旅行商问题，提出度量路段堵塞所带来时间损失的指标：路段堵塞损失值，并给出路段堵塞损失值的定义，给出路段堵塞损失值的具体计算方法。以降低路段堵塞所带来的时间损失为目标，建立了最优抗堵塞旅行路径选择模型。文中研究设计了时间复杂性为O(kn3)的算法进行求解，即分别计算起点到某个中间节点的局部路径、连接所有必经中间节点的局部路径及某一必经中间节点到终点的局部路径，将这三段局部路径连接在一起得到从起点出发经过多个必经中间节点后到达终点的最短路径。计算任一路径上每一条路段的堵塞损失值并找出最大值，每一条路径均可找出该最大值，从这些最大值中找出最小值，结合抗堵塞旅行路径本身的长度选择出最优抗堵塞旅行路径。本文为旅行者在交通网络中任一路段均可能发生突发性堵塞的条件下选择旅行路径，提供了一种新的思路，为交通网络管理提供了理论依据和实践借鉴。