一种基于相关的短时突发信号解调方法

高春芳，柯晓东，林 莉

(中国电子科技集团公司第三十六研究所，浙江 嘉兴 314033)

0 引 言

在短波通信中，作为一种新颖的通信方式，短时突发信号因其良好的自适应性、隐蔽性、抗干扰性等，在无线电通信领域得到了非常广泛的应用[1]。

在现代通信网络中，为了保证信息传输的安全性，每帧短时突发信号所携带的有效码元数量越来越少。传统的反馈环路解调已不再适合，而不需要收敛时间的前向开环解调是目前短时突发使用较多的方法。针对上述问题，本文提出了一种基于相关的短时突发信号前向开环解调。首先依据载波频偏估计算法、载波相偏估计算法完成信号载波同步处理；接着依据短时突发信号的定时同步算法完成突发信号定时同步处理，最后对定时同步后的数据进行抽取、判决，完成短时突发信号的解调处理。

这里提及的基于相关的短时突发信号解调流程如图1所示。其中，信号预处理主要用于完成信号的有效数据段提取和信号的重采样处理。

图1 基于相关的短时突发信号解调流程

1 短时突发信号的盲解调算法

短时突发信号的盲解调流程包括信号载波频偏估计、定时同步估计、抽取和判决3个步骤。

1.1 短时突发信号载波频偏估计

载波频偏估计包括载波频偏估计、载波相偏估计两步。当信号存在一定的载波频偏时，解调后基带信号的星座图会出现不停旋转的现象；当信号存在一定的载波相偏时，解调后的基带信号的星座图会偏转1个固定的角度。当信号存在载波频偏或载波相偏时，解调性能会迅速恶化[2]。因此，载波频偏估计是短时突发信号解调的一项重要技术，尤其在非合作短时突发信号解调中至关重要。

因短时突发信号的数据量少，不适合通过传统的反馈环路实现，因此选用不需要收敛时间的前向开环实现。

1.1.1 基于互相关频偏估计

对于星座图为2π/M旋转对称形式的信号，一般采用M次方去调制的方式进行去调制处理，去调制后的信号与本地单载波rcw(m)=A0exp[j(2πmfcwT+θ)]的互相关函数Rxy(m)可以表示为1个复单频信号，假设r(m)=a(m)exp[j(2πmf0T+θ)+wm]为经过定时误差校正后的有效信号序列[3]，则Rxy(m)可表示为：

Rxy(m)=|Am|exp[j(2πΔfmT)+w(m)]

(1)

式中：A0为常数；fcw表示单载波信号的频率；Δf=f0-fcw，表示去调制后信号与本地单载波的相对频偏；w(m)表示wm相关的零均值复值噪声；f0表示信号的频偏；T表示信号的符号周期；|Am|表示与a(m)有关的幅度值：

(2)

式中：N表示经过重采样后的有效数据长度。

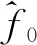
(3)

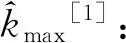
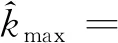
(4)

式中：Pxy(k0)为时刻k0的功率谱幅度值,k0为功率谱最大值对应的量化时刻，取值为整数；α=±1，当|Pxy(k0+1)|>|Pxy(k0-1)|时，α=1，否则α=-1。

1.1.2 基于自相关差分相偏估计

在上一节已经完成了对信号载波的频偏估计，那么就可以对信号进行频偏校正，图2为载波频偏校正框图。

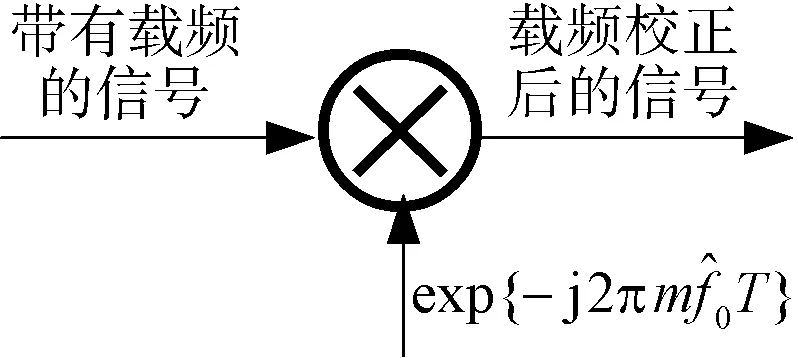
图2 载波频偏校正框图

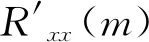
(5)

式中：η′(m)表示信号的相偏；w(m)表示零均值噪声。

用θ(m)表示信号的实际相偏，计算公式为：

(6)

1989年Kay在文献[3]中提出了一种基于相位差分运算的相偏估计算法。由式(6)可得相位差分Δη′(m)[2]：

Δη′(m)=θ(m)-θ(m-1)=

η′(m)-η′(m-1)+(w(m)-w(m-1))=

η′(m)-η′(m-1)+ξm

(7)

式中：ξm=w(m)-w(m-1),是与w(m)统计特性相同的零均值噪声，则由基于相位差分运算的相偏估计算法得相差估计表达式：

(8)

式中：W(m)表示平滑窗函数：

(9)

1.2 短波突发信号基于自相关的定时误差估计

信号定时同步是信号解调的关键技术之一，定时同步一般包括2个步骤：定时误差估计和定时校正，图3为信号解调定时同步框图。

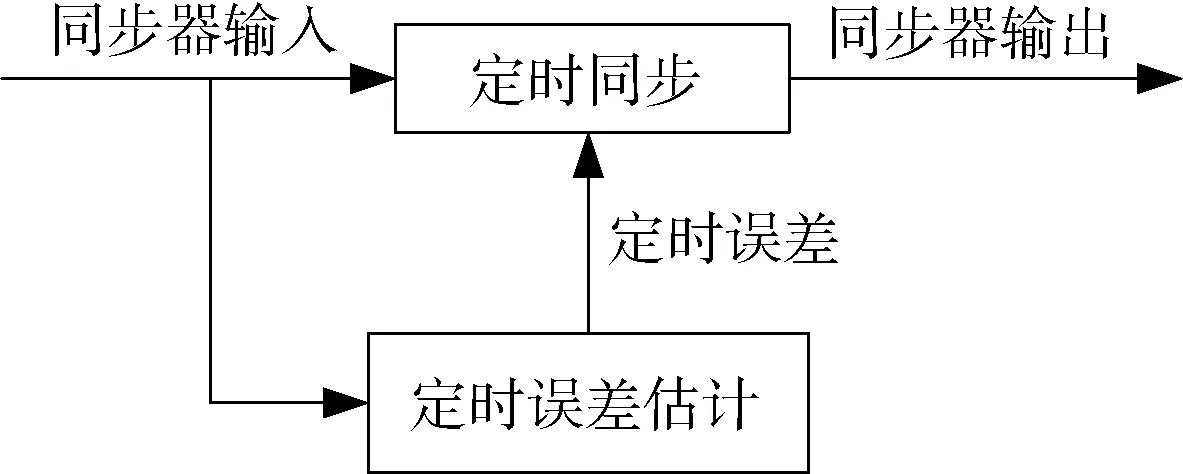
图3 信号解调定时同步框图

在定时误差估计之前，首先要依据采样速率和符号速率的转换，即信号重采样，要求采样速率是符号速率的整数倍关系。

数字通信中，在1个符号周期T内，各采样点之间的自相关性远大于相邻符号周期之间各采样点的自相关性。基于该准则，利用信号的自相关性来进行定时误差估计[3]。对进行突发检测后提取的有效信号进行整数P倍重采样处理后，得到的重采样数据r(n)再进行自相关运算，自相关函数Rdxx(n)为：

(10)

对信号序列r(n)的每个符号中的第l个采样点的自相关函数值求均值，可得：

(11)

式中：Ts表示采样间隔；rc(pTs-mT)表示以重采样P倍为周期的r(n)信号，0≤p≤P-1。

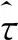
(12)

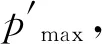
(13)

2 算法仿真验证

针对本章节提出的短时突发信号的盲解调算法进行性能仿真。

仿真1：仿真中使用输入数据调制类型为二进制相移键控(BPSK)突发信号零中频信号，信号频偏为2.5 kHz，符号速率为50 kHz，采样速率为600 kHz，每个符号内采12个点，快速傅里叶变换(FFT)点数为8 192，频率分辨率为73.242 2 Hz，突发周期为7.52 ms，突发时长为1.28 ms，突发符号个数64，Eb/N0=12 dB。图4为Eb/N0=12 dB的BPSK突发解调图，从图4可以看出，在信噪比为5 dB时，可以正确地对BPSK突发信号进行解调。

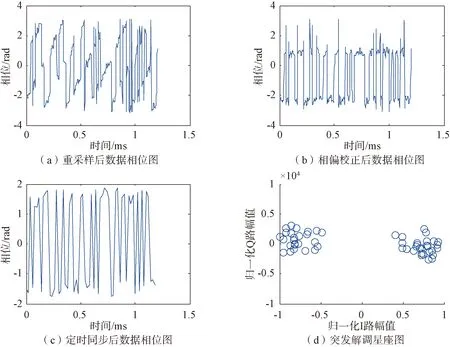
图4 Eb/N0=12 dB的BPSK突发解调

仿真2：仿真中使用输入数据调制类型为四进制相移键控(QPSK)突发信号零中频信号，信号频偏为2.5 kHz，符号速率为50 kHz，采样速率为600 kHz，每个符号内采12个点，FFT点数为8 192，频率分辨率为73.242 2 Hz，突发周期为7.52 ms，突发时长为1.28 ms，突发符号个数64，Eb/N0=12 dB。图5为Eb/N0=12 dB的QPSK突发解调图，从图5中可以看出，在Eb/N0=12 dB时，可以正确地对QPSK突发信号进行解调。

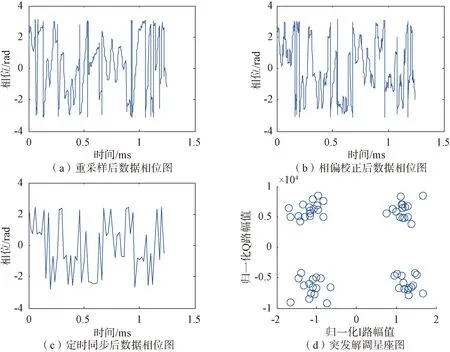
图5 Eb/N0=12 dB的QPSK突发解调

仿真3：仿真中使用输入数据调制类型为八进制相移键控(8PSK)突发信号零中频信号，信号频偏为2.5 kHz，符号速率为50 kHz，采样速率为600 kHz，每个符号内采12个点，FFT点数为8 192，频率分辨率为73.242 2 Hz，突发周期为7.52 ms，突发时长为1.28 ms，突发符号个数64，Eb/N0=14 dB。图6为Eb/N0=14 dB的8PSK突发解调图，从图6可以看出，在Eb/N0=12 dB时，可以正确地对8PSK突发信号进行解调。

图6 Eb/N0=14 dB的8PSK突发解调

仿真4：对本章节提出的短时突发信号的盲解调算法误码率性能仿真，设置采样率采样速率为600 kHz，信号频偏为2.5 kHz，符号速率50 kHz，FFT点数为8 192，成形滤波器为根升余弦滚降系0.35，每种调制类型信号分别进行 100 次实验。图7给出了在不同信噪比下，调制样式为BPSK、QPSK、8PSK的解调误码率，图8给出了在不同信噪比下，调制样式为BPSK、QPSK、8PSK的理论解调误码率曲线图，其中BPSK和QPSK理论误码率曲线重合。

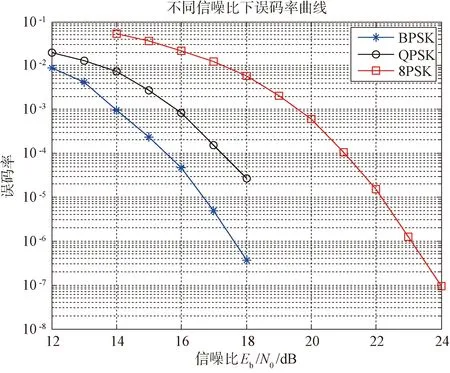
图7 不同Eb/N0下各调制样式的误码率曲线

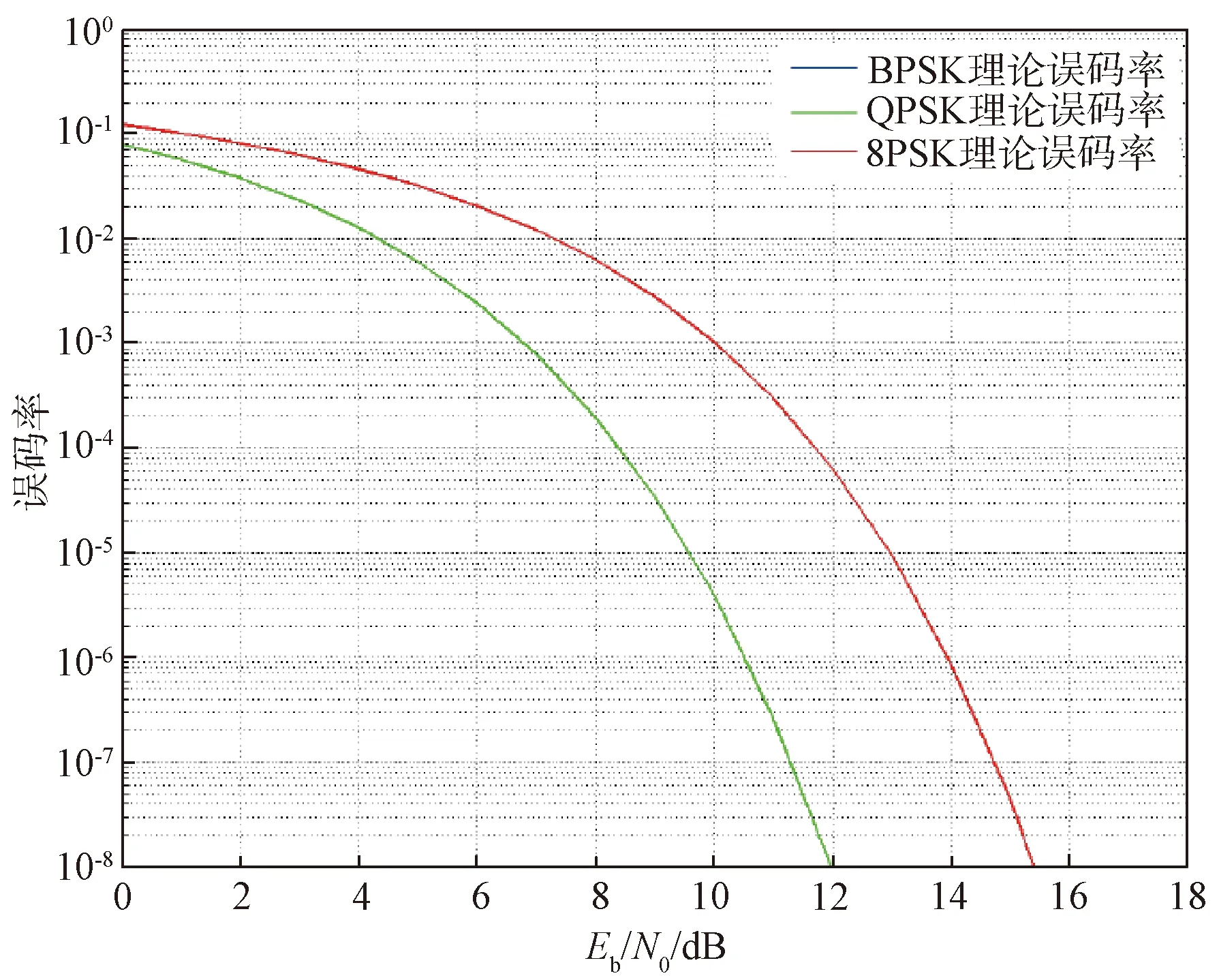
图8 不同Eb/N0下各调制样式的理论误码率曲线

由仿真结果可见，短时突发BPSK、QPSK以及8PSK的解调误码率与常规连续BPSK、QPSK以及8PSK信号的误码率存在一定差距，这是由于常规连续BPSK、QPSK以及8PSK信号解调是采用反馈环路进行解调，而短时突发BPSK、QPSK以及8PSK的解调是通过前向开环实现的。由于短时突发信号的数据量少，不适合使用传统的反馈环路实现，因此选用不需要收敛时间的前向开环实现。

3 结束语

采用基于相关的短时突发信号解调方法，在低信噪比下，首先依据基于互相关频偏估计和基于自相关差分相偏估计完成突发信号的载频校正，其次使用基于自相关的定时误差估计完成突发信号的定时同步，然后对定时同步后的数据进行抽样和判决，完成突发信号的解调，最后进行了算法仿真验证。仿真证明了短时突发BPSK、QPSK以及8PSK的解调误码率曲线与理论值有一定的差距，具体原因是解调采用了前向开环实现。