光电有源定位法精度分析及提升方法研究

黄小帅 王增发

（中国科学院长春光学精密机械与物理研究所 航空成像与测量技术研究一部 吉林省长春市 130033）

目前空中平台对目标的定位方法主要分为两种体制，一种是电子/雷达定位法，另一种是光电定位的方法。前者利用 的平台位置信息是通过目标和测试平台的电磁波相位、频率等物理量解算的距离和利用方向参数[1]方位信息进行定位[2]，这些物理量本身分辨力和精度很高，能够达到mm 甚至μm 数量级，所以解算出来的目标位置信息精度较高；光电定位法主要是依据测试平台位置信息、姿态信息以及相对目标的距离信息等物理量进行解算，得到目标的经度、纬度和高度的位置信息，这些物理量本身精度和分辨力相对低一些，角度误差和测距误差对10km 外的目标折算到距离，误差能够达到m 数量级。与电子定位方法的误差相比光电定位的误差是由测量方法导致的系统误差，这是两种测量体制带来的固有误差，只能不断优化定位策略来降低误差影响大的物理量对结果精度的影响，并通过增加一定测量次数来降低随机误差对定位结果的影响。而这个优化的增加测量次数的过程势必会牺牲算法效率和实时性，所以光电定位的“快和准”是无法同时满足的矛盾体。

1 光电定位体系

在光电定位的分类中，按照直接测距法和间接测距法把光电定位分为主动法定位和被动法定位[3]。前者平台主动向目标辐射激光源，利用激光雷达等设备对目标进行直接测距[4]，再利用这个测距值结合其他测量参数解算目标位置信息；后者无法直接获得平台相对目标的距离信息，而是通过多航迹点和图像匹配等方法[5]间接获得目标的距离信息，再通过与主动法定位类似的算法解算目标的位置信息。因为主动法和被动法本质区别就是在探测平台上是否对目标主动辐射能量来直接测得平台和目标的相对距离，所以也可称为有源法定位和无源法定位。

除了获取目标距离信息的方法有所不同，两种定位法的光电定位的核心都为坐标转换。目标定位的结果就是确定目标在一个统一坐标系中的空间位置，想要得到目标的经度、纬度和高度，相当于用已知的条件和测量到的参数列矩阵方程进行求解，最终得到目标的位置信息。这些参数是通过不同平台的测量数据，每个平台参考坐标系不同，需要将它们最终统一到同一个坐标系下，所以定位的核心为坐标转换。下面以激光测距定位法作为定位核心算法，推导这个过程。

2 光电有源定位法推导和精度分析

2.1 坐标系的引入

（1）WGS-84 大地坐标系[6]：以参考椭球的中心O 为原点，椭球旋转轴ON 位北极，并且位大地坐标系的Z 轴。

（2）地球坐标系[7]：地球坐标系又称为空间直角坐标系，原点在地球中心，Z 轴与地球自转轴重合，X、Y 轴互相垂直并固定于赤道面上。

（3）地理坐标系[8]：以定位站为圆心，X轴沿原点纬线切线向东，Y 轴沿原点经线切线向北，Z 轴垂直于原点所在平面指向天顶。

图1：光电定位流程图

图2：各项参数的真值

图3：地球相关参数的理论真值

（4）载机坐标系[9]：原点在无人机质心位置，X轴位无人机航向，Y 轴指向右翼。

（5）光电平台坐标系：与载机坐标系为同一坐标系，当刚性安装到飞机上时，会因为安装误差产生微小的旋转和偏移。

为了计算方便，以上坐标系均采用右手坐标系。

2.2 定位方程的推导

在进行定位方程推导之前，需要首先推导坐标转换的矩阵变换方程作为先验知识。以二维坐标系为例，三维右手坐标系是二维坐标系的推广。平面直角坐标系xoy 经过逆时针旋转θ 得到x′oy′坐标系，通过平面上任意一点P 推导坐标转换的方程。

用极坐标法能够很好的反映坐标旋转关系，P 点在原坐标系上表示为P(x0,y0)。

其中R 为P 点到原点的欧氏距离。在x′oy′坐标系上表示为P(x'0,y'0)。

则将（1）式代入（2）式，并转换为矩阵相乘的形式可得：

从二维坐标系可推广到三维坐标系。为了计算方便，在坐标转换过程需要将矩阵增加一维将线性空间的笛卡尔坐标系转换到仿射空间的齐次坐标系，这样能够方便用矩阵的乘法表示坐标的旋转、平移和缩放。通过这些先验知识对光电定位的模型进行推导。

光电定位流程如图 1 所示。

当光电平台发现目标时，转动平台保持目标在图像中心，打开激光雷达进行激光测距，得到此时平台相对于零位的俯仰角α（水平为0，上正下负）和方位角λ 以及测距值R。则目标在光电平台坐标系下的坐标值为：

齐次坐标法通过仿射空间从平台坐标系转换到大地坐标系如下：

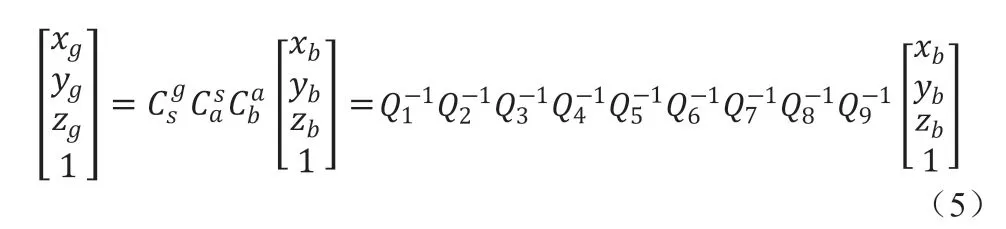
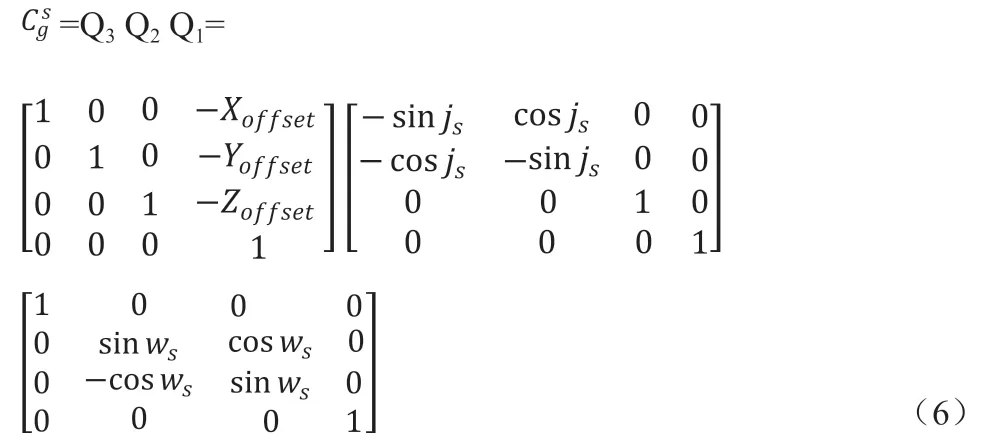
其中js、ws是飞机经纬值。其中Xoffset、Yoffset、Zoffset见公式（7）：

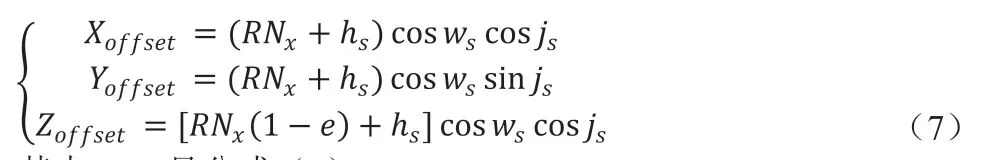
其中RNx见公式（8）：

其中a 是地球长半轴，b 是地球短半轴，e 是地球第一偏心率。

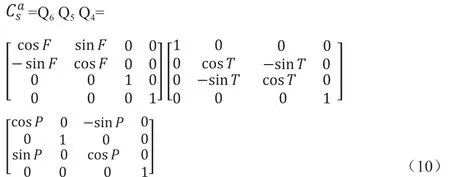
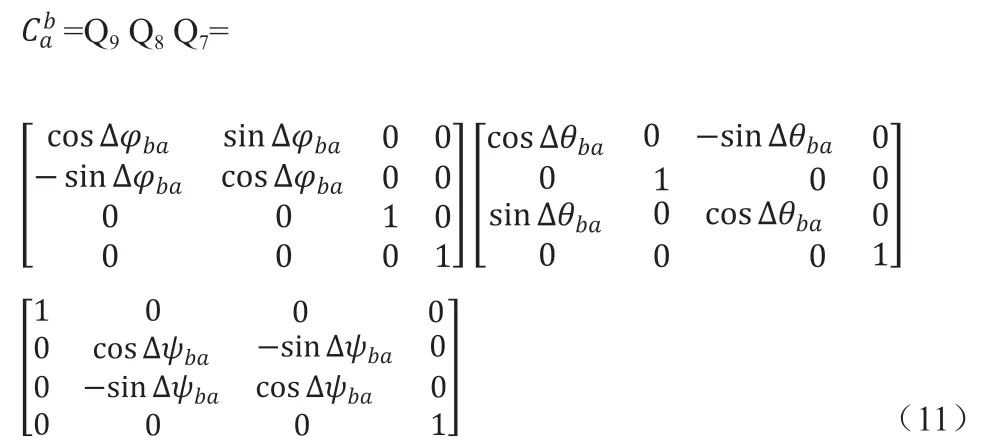
其中，Δφba、Δθba、Δψba分别为减振器的横滚角、俯仰角和偏航角。当光电平台通过减振器与载机刚性连接时，Δφba、Δθba、Δψba表示固定的安装误差，能够比较准确的测量出来，可以通过坐标转换修订；当光电平台与载机为柔性连接时，可在光电平台内安装子惯性测量单元（Inertial Measurement Unit，以下简称IMU），则认为为单位矩阵E，具体的论述会在第3 章展开，这里采用子IMU 的方法进行计算。

最后，地球坐标系转换为大地坐标系，求出目标位于大地坐标系中的坐标值 (B,L,H) 。

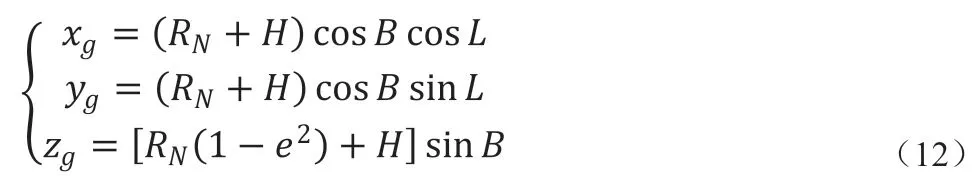
其中，B 是大地纬度，RN是地球卯酉圈曲率半径。

若由地球坐标系转换为大地坐标系，则近似的数学关系为：

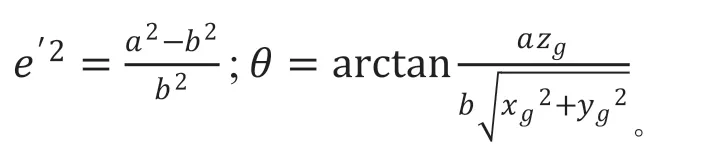
当然未来得到更加精确的位置信息，则可以通过迭代法取得精确的结果。

直到：

其中ε1、ε2，根据要求的精度设定，经过多次仿真发现，10-6的精度一般需要4~5 次就能实现。迭代初值为：

图4：飞机位置误差分布直方图

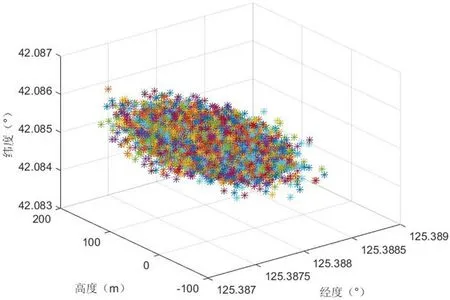
图5：定位误差分布仿真图

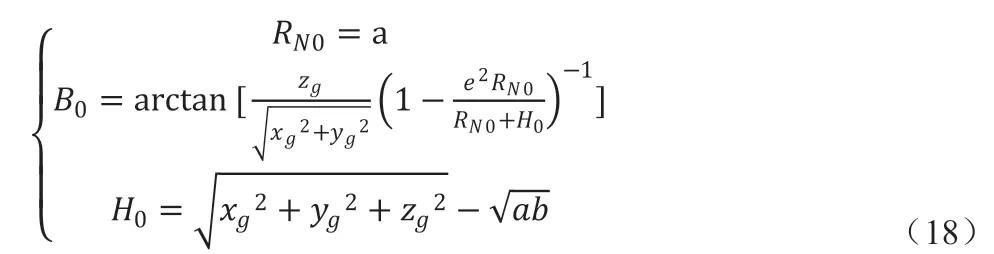
最终经过上述过程解算得到目标的经度、纬度和高度值的位置信息。

2.3 定位精度分析

光电定位中所有参数都是测量值，在测量过程中无法避免的会产生误差，影响最终定位精度。首先根据上一节定位方程推导结果分析一下定位所需要的参数及其误差来源。

（1）光电平台测得的方位角和俯仰角。这两个角度值是由平台角度传感器测得，根据当前角度测量技术，采用16 位角度编码器测角，分辨力达19.77″，测角精度σ1=σ2=0.05°实验室测得为正态分布；

（2）光电平台测得目标到平台的直线距离。由激光测距机测得，实验室测得误差呈正态分布，精度σ3=5m@25Km；

（3）飞机姿态角，包括飞机横滚角、俯仰角和偏航角，需要分情况讨论。上文提到，当光电平台与飞机刚性连接时，飞机姿态角由飞机主IMU 测得；而当光电平台内部有一个与主IMU 捷联的子IMU 时，平台内子IMU 可以直接解算飞机的位置信息和姿态信息。通过自动校靶[10]，能够通过飞机主IMU 对平台子IMU 陀螺漂移进行补偿，保证平台子IMU 姿态信息测量精度的稳定性。实验室测得为正态分布，其中俯仰角和横滚角的精度σ4=σ5=0.05°，航向角精度σ6=0.1°。

（4）飞机的位置信息由飞机GPS/北斗信号获得。通过三星定位原理在飞机上安装定位信号接收机，进行飞机实时定位。其中位置结果通过经度纬度和高度体现，实验室测得为正态分布，经纬度的精度σ7=σ8=0.0001°，高度的精度σ9=10m。

这些测量参数来源不同，相互独立，正是通过定位方程进行传递，影响最终目标的定位精度。而最终定位精度的计算方法主要有两种方法：直接法和间接法。直接法可以需要将搭建相关平台，对地面上精准位置的目标进行多次定位，而要想通过定位测量值与真值比较，根据误差理论，需要进行200~1000 次等精度测量试验才能得到定位误差的概率分布函数，实现难度大；间接法通过多元定位方程，通过飞行误差传递的过程，得到每一项参数的误差对定位精度的影响；既可以通过全微分法分析偏差和标准差结果，也可以通过计算机模拟的方法进行分析，通过分析每个环节的误差得到最终的定位误差，本文采用间接法对定位精度进行分析。假设定位误差为∆Y，xi为每一项参数的真值，∆xi未每一项参数的误差，f 为定位方程映射规则，则

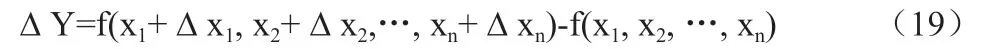
根据公式（5）和主、子IMU 理论，定位方程中至少需要连乘6 个3×3 的矩阵，最终得到的定位方程式为每一项是多个三角函数的相乘的多项式，用全微分法估算定位误差计算庞杂而且分析难度很大，所以采用蒙特卡洛方法（Monte Carlo method）。作为统计模拟方法，采用计算机生成大量随机数据的方法对结果进行估计，得到误差的概率分布函数。

分别根据误差正态分布∆xi~N(0，σi)得到每个参数对应的10000 组值作为参数的误差。首先假设σi=0，即如果没有误差，得到的定位值为真值。各参数真值如图 2 所示。要计算定位经度还需要一些理论真值作为先验知识，这些理论真值如所示。将这些参数带入定位公式计算得到目标的经度为125.38781°，纬度为42.08505°，高度为57.82988m。地球相关参数的理论真值如图3所示。

10000组飞机位置误差分布直方图如图4 所示，飞机姿态角和平台测量角以及定位等参数误差分布与之类似。

将误差加入，经过10000 次的蒙特卡洛仿真试验，得到最终目标定位结果分布如图 5 所示。

为了更直观，将目标定位的经度、纬度和高度10000 组结果分布进行统计，如图6 所示。

可以看出定位结果分布也呈正态分布，进而得到经度误差为σB=1.94408×10-4°，纬度误差为σL=4.43348×10-4°，高度误差为σH=33.83841m。根据公式（12）折算为空间欧氏距离误差为σr=63.37698m，相对误差为欧式距离公式为：

图6：目标定位结果分布直方图

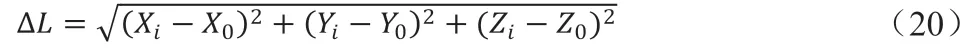
其中Xi，Yi，Zi 为定位测量值，X0，Y0，Z0 为定位真值。根据误差理论知，定位误差呈正态非同分布，欧式距离分布为瑞利分布如图 7 所示。

2.4 小结

激光测距结合测角有源定位法作为本文核心算法，具有算法效率高，实时性好，工程可实现性强，成本适中，环境适应性强，在现代各环节高精度传感器测量的条件下，能够保证定位范围的情况下，实现很高的定位精度。通过对该算法的定位精度分析可知，光电定位是各个环节综合影响的结果，需要结合实际的使用场景，分析各个测量环节对结果的影响。

进一步提升定位精度主要考虑两方面：最简单而直接的方法是，在一定的成本约束下，通过采用更高性能传感器提高各个环节参数的测量精度，这个方法不在本文研究的范围内；第二种方法就是从系统和算法的角度出发，分析误差的根本来源，通过结合一定策略和算法削弱这些误差对精度的影响同时提升定位的能力，这也是下一章的重点。

3 定位能力提升措施分析

除了之前提到的测量随机误差对定位结果影响，由于测量策略造成的系统误差与随机误差同时作用的情况下带来的误差对目标定位有很大影响，需要对核心算法进行改进。

3.1 角度误差带来的拓宽效应

根据误差理论不确定度的合成，有

分析角度误差包括姿态角测量误差、测距误差以及飞机的位置误差，通过控制变量法，只取一类误差为变量，其他误差为0 的情况下分析定位精度，发现各个误差的合成符合公式（21），而且角度误差带来的定位距离误差是定位误差最主要来源。

假设飞行高度为7000m，角度误差为1mrad，则对垂直向下的目标进行定位是，角度误差带来的偏移量约为±7m，同样飞行高度，当斜距为10000m 时，同样的角度误差带来的偏移量约为±10m，而且随着倾斜角度α 和飞机距离目标的距离R 的增大，这种角度误差带来的拓宽效应愈发明显。而根据实际使用场景，飞机飞行高度一定，飞机需要与目标保持安全距离，这个安全距离是远大于飞机飞行高度的，所以飞机多时候是无法对目标垂直定位的，这种拓宽效应也是无法消除的。而减弱这种拓宽效应主要有两种措施：

图7：目标定位测量值与真值距离分布直方图

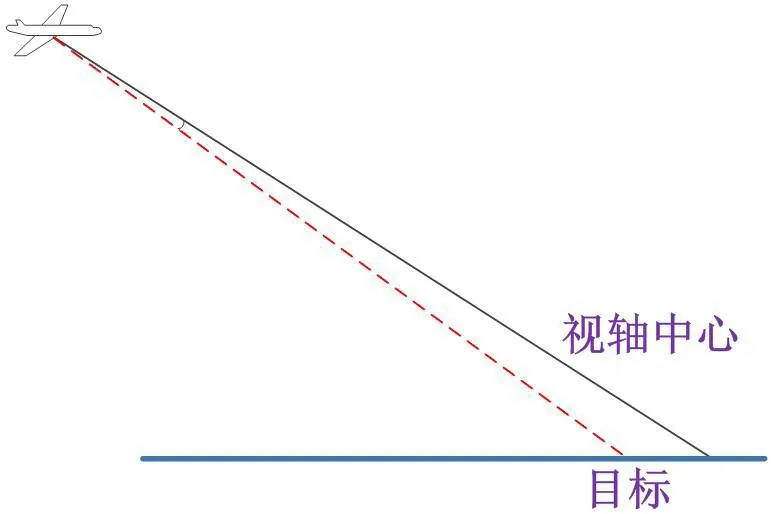
图8：载机振动带来的视轴中心角度偏移

（1）以飞行高度极限值和安全距离极限值为定位阈值对目标定位，低于飞行距离和超过安全距离对目标定位都会加剧角度误差拓宽效应的影响。

（2）使用多点交汇定位（至少三点），结合最小二乘滤波器对目标进行定位。

将飞机的导航位置信息根据公式（12）转换到地球空间直角坐标系下，得到飞机的空间直角坐标(Xpi, Ypi, Zpi),(i=1,2,3….n,n ≥3)，当n=3 时，则

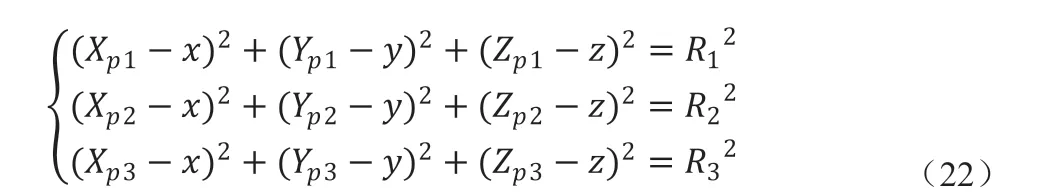
Ri,(i=1,2,3….n,n ≥3)为激光测距值，通过公式（22），可以得到目标在地球空间直角坐标系下的坐标值(x,y,z)，再根据公式（14）或者公式（15）~（18）得到目标的经度、纬度和高度坐标值。

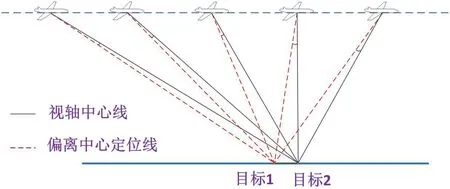
图9：偏离视轴中心定位

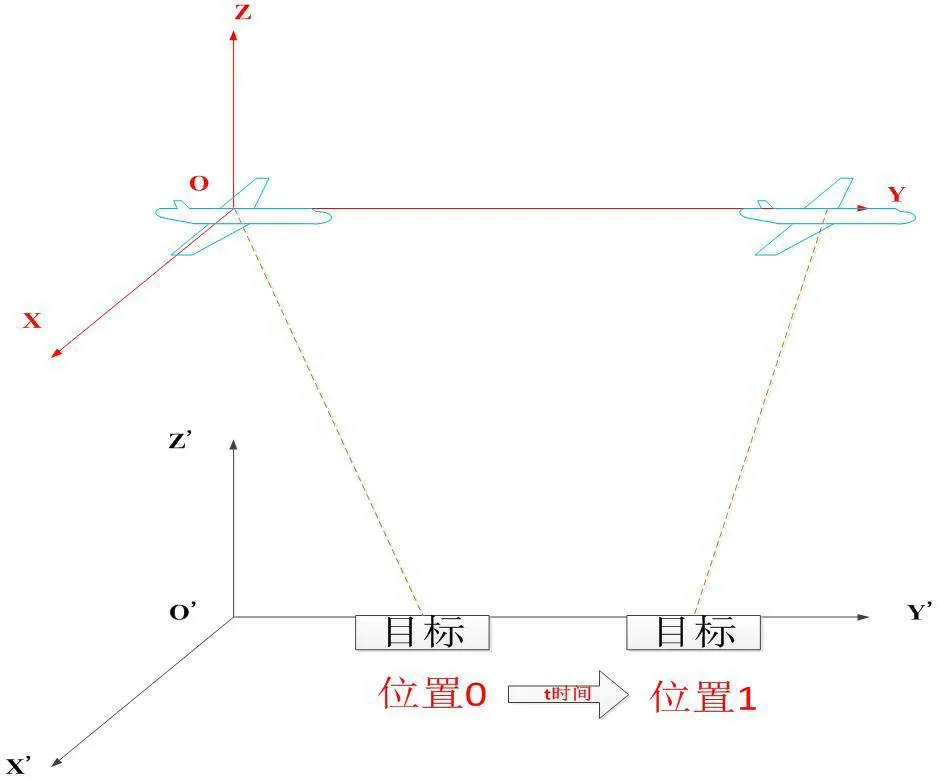
图10：卡尔曼滤波定位目标状态

当n>3，由于测量次数n 大于未知量参数t（t=3），采用最小二乘滤波器对数据估计，由于公式中含有平方项，所以模型为非线性的最小二乘滤波器，采取的方法为：首先根据公式（21）用方程组得到目标定位的初值；然后对(Xpi-x)2+(Ypi-y)2+(Zpi-z)2=Ri2(i=4,5….,n,n>3)，取泰勒级数展开的一阶近似，将非线性模型转换为线性最小二乘滤波器，再经过多次迭代，得到定位精确值。

方法（2）可以消除角度误差拓宽带来的影响，但是多次引入了飞机位置误差和测距误差。一方面配合最小二乘法滤波器对数据的筛选估计，可以进一步消除随机误差的影响，另一方面，如果飞机位置精度和测距精度高，对结果影响不大，否则，精度还有一定下降。这个方法最大的缺陷是单机多点定位时，定位实时性差，需要规划围绕目标较长的路径（路径太短，误差大），因此只能定位固定的目标；而采取多机定位，在任务阶段至少需要三架飞机，且测距和飞机定位状态基本一致，并且需要三架飞机的时统相匹配。所以方法（2）在同等条件下定位精度虽然可以更高，但是时间成本或者任务成本也必然更高。

为了既能提高定位精度又能减小成本，结合核心算法做出改进。首先利用方法（1）得到一定精度的目标定位信息作为初值；然后在飞机航迹点上任意一点进行激光测距，得到(Xp-x)2+(Yp-y)2+(Zpz)2=R2。然后对此公式用泰勒一级展开截断，按照线性最小二乘法对定位结果进行迭代，由于初值结果精度较高，迭代次数很少算法效率会很高，而且也极大削弱了角度误差的影响。也可通过双机交汇定位进一步提升定位的效率和实时性，与方法（2）相比，保证了定位精度和实时性的同时降低了成本。

3.2 载机振动的影响

光电平台是根据图像进行采集和定位。首先需要平台观察到目标，载机的振动会影响平台的视轴稳定性，反映在图像上会使得目标质心与图像中心存在像素点的偏移，这个偏移量反映在平台上可以认为是角度的偏移，进而影响定位精度，如图 8 所示。

当对目标定位期间为飞机振动较大的时刻，则可能为定位结果引入无法预料的误差。所以光电平台需要良好的抗振环境，减振器的使用就是光电平台必不可少的一部分。而减振器的安装会引入安装误差，这个安装误差属于系统误差，可以在地面调试的时候测量并进行补偿，如公式（11）所示，将安装误差代入公式进行定位计算，则可以消除振动带来的影响。

当飞机振动环境恶劣，刚性连接减振器对飞机振动传递大，且长时间工作会对减振器产生不可逆的损伤，所以平台减振器与载机为柔性连接。而飞机的振动来源复杂，无法进行量化，所以对于平台定位来说是不可预计且无法忽略的重要误差来源。采取的措施为在光电平台内部安装子IMU 来消除振动带来的影响。而且子IMU能够取代主IMU 的功能，即获得光电平台的姿态信息和位置信息，则公式（11）的结果为1。这一方法直接的优点就是减少一级误差传递，提高了定位精度。

由于在平台内放置了IMU，为了尽量不占用成像系统空间，采用体积小的IMU。在进行标校后的子IMU 姿态测量和位置信息获取与飞机主IMU 精度相当；在一定时间后，随着子IMU 内部陀螺的漂移，导致测量精度严重下降，则需要将飞机内高稳定性激光材料的IMU 解算数据结合高精度定位定姿系统，通过平台自动的动态校靶功能抑制补偿陀螺漂移带来的姿态误差，保证定位精度。安装子IMU 的方法也保证在每次拆卸维修光电平台后安装到飞机上不用重新测量安装偏差进行补偿，只需要按照一定流程进行校靶和对齐就能进行飞行和定位，缩短任务准备阶段的时间，所以在第2章的推导使用了子IMU 的方法。当然子IMU 压缩了成像系统空间，可导致成像作用距离减小，而光电平台主要的任务是获取图像，因此，需要在子IMU 的精度和体积上进行一定取舍。

3.3 非视轴中心定位

当对多个目标定位时，两个目标位置关系如所示，其中对目标2 在视轴中心进行定位，则目标1 偏离视轴中心。反映在图像上就是目标2 在图像正中心，而目标1 在距离图像中心会有几个像素点的偏移。

由图9 可以看出，在相同飞行高度上，角度偏移量与光电平台的俯仰角度有关，当俯仰角越小时，角度偏移量越小，反映在像素偏移量上越小，测量精度也越低。所以对于非视轴中心目标的定位也在保证安全距离情况下，尽可能大的俯仰角，这与减弱角度误差拓宽效应的策略相同。当然，也可以将目标放置到视轴中心进行定位来确保最优的定位精度。

3.4 运动目标的定位

目前所使用的定位方法只针对固定目标有效，而对运动目标，无法对目标的运动趋势进行预测。提到状态预测自然而然想到的是卡尔曼滤波器[11]，而对于定位系统来说，系统状态方程和观测方程为非线性方程[12]。所以采用扩展卡尔曼滤波（Extended Kalman Filter, EKF），通过非线性模型在状态值附近泰勒级数展开并取一阶截断进行线性化，并假设线性化后状态仍然服从高斯分布，在对其使用卡尔曼滤波获得状态估计。

考虑一种简单的情况：假设目标与飞机同方向，速度大小不同做匀速直线运动，如图 10 图 9 飞机对目标2 进行定位和跟踪。假设k 时刻目标相对载机的运动状态向量为其中[xk,yk,zk]和分别对应目标相对载机的距离地球空间直角坐标系的三轴分量及其速度分量，而载机每个时刻的位置和速度是已知的。

卡尔曼滤波主要需要两个方程对目标定位的结果进行预测，而假设每个参数和变量都遵循高斯分布，则有公式：

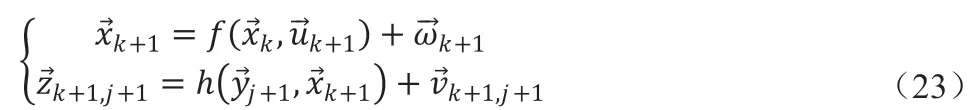
忽略下标j 得到：

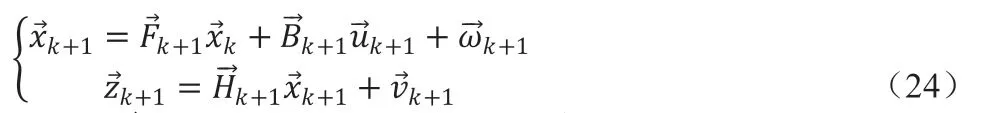
本例通过载机与目标相对的位移与速度关系，可得到目标的运动状态方程：

其中，

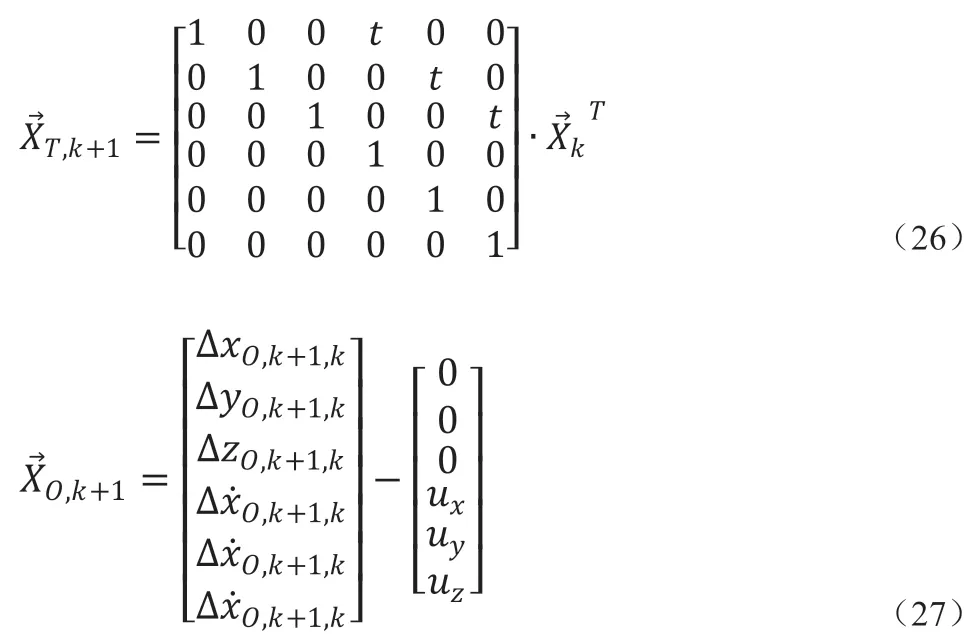
根据光电平台的测角量反映目标的映射光学得到测量方程：

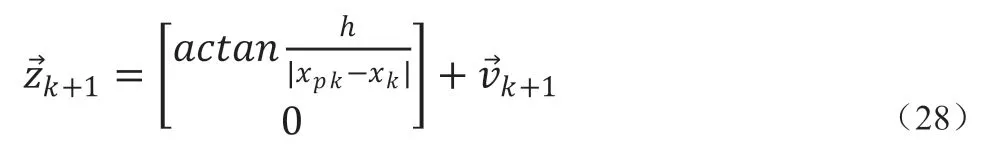
其中，h 为飞机高度，xpk 为飞机k 时刻x 轴坐标。

对方程（27）求导可得到雅可比矩阵，通过有源定位法得到初值，将初值代入EKF 的公式进行迭代，得到 在需要任意时刻的值，就能预测目标的位置和速度信息。

通过本例的简单推导，就能对一般情况下运动目标定位进行推广。结合核心算法和第1 节的提示，将核心算法得到的定位值作为初值，目标在地球直角坐标系下的状态为状态方程，以核心算法的方程作为观测方程，在航向上多个航迹点上使用扩展卡尔曼滤波进行迭代解算，能够实现对目标位置、速度等参数的测量和预测。而为了减小计算量，提高运算效率并保证预测精度，可以根据需求和实际使用环境规划航行轨迹，例如使载机围绕目标匀速直线运动或匀速圆周运动等。本方法可以与第1 节最小二乘法同步使用，保证定位精度的同时实现对运动目标的定位。

3.5 小结

本章结合实际，对系统进行分析，提出了在核心算法基础上，平台内加装子IMU，合理规划航线，并在航线的航迹点上结合最小二乘法和扩展卡尔曼滤波法，在保证定位效率的同时，提高了定位精度和定位能力。

4 结论

在光电载荷定位需求上出发，推导了可以广泛应用的测角、激光测距有源法的光电定位方法作为核心算法，并分析了定位的误差来源。以仿射空间的齐次坐标转换为核心的光电定位算法有效的通过采用蒙特卡洛方法对定位精度进行仿真，以现阶段能够达到的各项参数的精度指标，最终目标定位能够实现0.25%@25Km 的相对误差。并对定位实际情况分析，提出了结合最小二乘滤波器的激光测距有源法的光电定位方法，有效减少角度误差带来的影响；通过子IMU 的安装消除载机震动带来的随机误差；设置一定的定位策略减小非视轴中心目标定位的误差；并结合拓展卡尔曼滤波的算法法实现对运动目标的定位，提升了定位能力。