基于GeoGebra双曲抛物面直母线的动态绘制

梁赵套 王晓红

（石河子大学理学院 新疆维吾尔自治区石河子市 832003）

解析几何是大学数学的基础课程之一，它建立了抽象与具象的“桥梁”，主要体现在几何图形的直观性，其中曲线、曲面问题是研究重点。而空间几何图形的动态输出将会更好地体现几何直观性，从而提高学生的空间想象能力。《解析几何》中常用“平行截割法”研究三维曲面，即用一族平行于坐标平面的平面来截割曲面研究截口曲线是怎样变化的，通过分析这一族截口曲线的变化情况，想象方程所表示曲面的整体形状，主要思想是把复杂的三维图形归结为二维曲线[1]。《微分几何》更是以曲线论、曲面论为其主要内容，主要处理方法是活动标架法[2]。直纹面是曲面中较为特殊的情形，它是由两族直线移动生成的曲面。尽管直纹面是经典微分几何领域的相关内容，但是仍可以使用解析几何中的部分方法对它进行研究。黄保军通过综合分析截痕的变化来认识曲面的形状，还通过分析曲面的内部结构来把握其几何特征，详细论证了双曲抛物面是遵循一定规律的动直线的运动轨迹，直观揭示其几何特征[3]。历晨晨等人讨论了一种特殊直纹面与平面的变换方式[4]。董志龙等人从理论角度总结了直纹二次曲面在建筑、机械等多个领域的典型应用，并结合直纹面的数学性质分析其实际应用效果[5]。直纹面分为可展曲面与不可展曲面，其中不可展曲面中有关双曲抛物面直母线的研究相对较少。李国生利用数形结合的数学思想深入探究了双曲抛物面的几何性质、图示方法及数学方程的建立[6]。桂国祥，刘雅芸列举了双曲抛物面的实际应用[7]。在建筑、电力、水利、运输等工程方面，可以找到直纹面的数学模型，如旧金山圣玛丽教堂的设计应用了双曲抛物面的相关性质。近些年来，数学软件GeoGebra 在动态三维图形的绘制方面更加简捷[8]。施永新、闫湛等人根据“平行截割法”手工绘出三维曲面的图形，借助GeoGebra 软件动态展示截口曲线的变化过程[9-10]。然而，用二次曲面直母线来绘制空间曲面，并使其动态化的研究相对较少。由于二次曲面中部分曲面可以由一条直线按照某种规律运动所生成，根据这一思路结合平截线的思想，我们将探究是否可以利用“平行截割法”对双曲抛物面的直母线进行研究，即利用平行平面与双曲抛物面的交线刻画直母线。

设双曲抛物面S 的方程为：

其中a>0，b>0。

一般情况下，如果一空间图形的方程中仅含一次项，那么该图形为一平面。倘若某一平行平面始终与某一空间曲面的交线是直线，则空间曲面可由该直线生成。

定理1 在与双曲抛物面（1）相交的无数平面中，总存在两族平行平面与双曲抛物面的交线始终是直线，且该直线可生成双曲抛物面。

图1：双曲抛物面与平面的交线

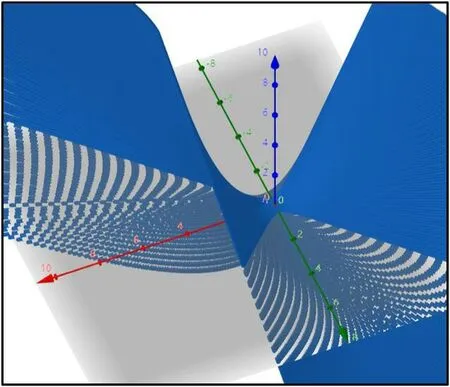
图2：一族直线生成双曲抛物面

证明 想找到双曲抛物面（1），设一族平行平面的其中一个平面方程为：

其中c 是常量。但可通过控制c 得到无穷多个平行的平面。

联立（1）（2）解得：

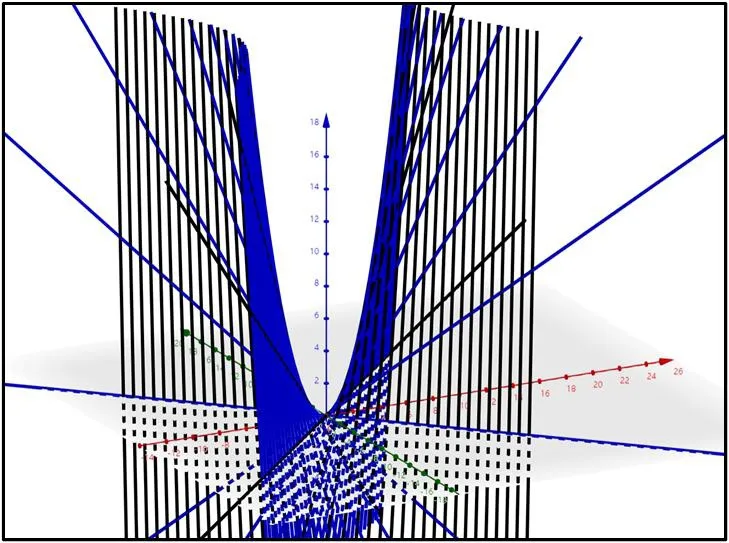
图3：相交的异族直母线

（3）式仅含有y、z，说明该方程表示的是一平面。

令（3）与（2）相交，交线显然是直线。该直线的方程为：

同理可证，另一族平行平面的其中一个平面方程为bx-ay=c，该平面与双曲抛物面（1）的交线也是直线，且该直线的方程为：

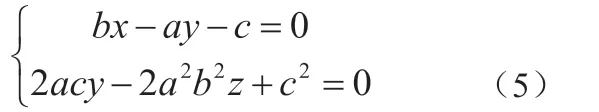
由于平行平面方程中c 是连续可变的，通过不断移动，可得到无数条与双曲抛物面相交的直线，那么就说明该直线可构成双曲抛物面。下面将从直母线的角度给出严格的证明。

给出双曲抛物面（1）两族直母线的方程为：

要想证明两族交线（3）（4）可生成双曲抛物面（1），只需证明其中一族是双曲抛物面的一族直母线即可。不妨先取交线（3）和u 族直母线（6）进行验证。

已知方程（3），给出方程（3）的方向数为：

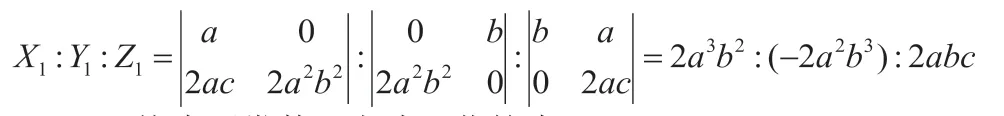
又a、b 均为正常数，上式可化简为：

设（x1,y1,z1）是方程（3）上的点，取有：

另一方面，我们可以求出u 族直母线（6）的方向数为：

设（x2,y2,z2）是方程（6）上的点，取x2=a，有：

由于c，u，v 均是可变的，联立（8）（9）（10）（11）得下列等式：

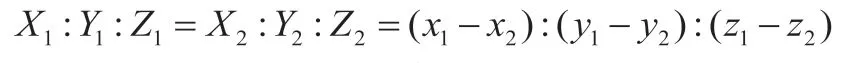
根据直线重合的充分必要条件可知，在与双曲抛物面相交的无数平面中，总存在两族平行平面与双曲抛物面的交线始终是直线，且平行平面的方程为bx+ay=c 或bx-ay=c，双曲抛物面可由该直线构成。

在实际教学中，根据定理1 的构造原理，仅凭空间想象难以绘出直线移动生成曲面的过程，借助GeoGebra 软件能动态展示平行平面移动时与双曲抛物面截线的变化过程，可起到传统教学手段不能呈现的直观效果。下面给出利用GeoGebra 绘制双曲抛物面由直母线动态形成的详细过程，此过程清晰明了，绘制效果直观易懂。

双曲抛物面一族直母线形成的绘制步骤：生成双曲抛物面（1）的整体图形，选3D 绘图区，在输入框中输入：再输入3x-2y=c，3x-2y=c 生成一平面，该平面是截平面；利用“相交曲线”，取双曲抛物面与平面的交线（3）（4），如图 1 所示；隐藏原本的双曲抛物面及平面，仅留下上一步骤的交线（3）（4）；点击“播放”，生成动态形成图；右击交线（直母线），勾选“显示轨迹”，重复上一步骤，可得到带有移动轨迹的动态生成图。同理，绘制出双曲抛物面的两族直母线及运动轨迹，如图 2 所示。

由于双曲抛物面上异族的任意两直母线必相交，结合上述绘制过程，我们可以得到相应的几何直观图，如图 3 所示。

利用GeoGebra 在几何直观上辅助双曲抛物面的直母线教学，为教师教授直纹面内容提供了新思路，为学生理解直纹面提供了新方法，达到事半功倍的效果。