丰盈规律探究过程 玉成学生一生“童真”

郁丽艳

【摘要】丰盈规律探究过程，让学生思维得以发展，让其经验得以积淀，创建适合每位学生的“童真课堂”，是笔者从教以来的价值追求。笔者认为，教师应有鲜明的儿童立场，能真正基于儿童的特点，丰盈教学过程，帮助学生发现知识的本质，真正让知识鲜活起来，让学习内容丰富起来，只有这样，才能玉成学生一生“童真”。

【关键词】规律探究;小学数学;教学策略;童真

【基金项目】本文系2019年江苏省前瞻性教学改革实验项目“课堂玉成一生‘童真——‘童真课堂建设”的阶段性研究成果。

一、“童化”学材，顺应儿童的思维发展特点

规律探索是数学教学内容之一，需要学生通过观察、分析、综合归纳和概括来探寻变化的事物中存在的不变的关系。怎样丰盈规律探究的过程，让规律探究课型灵动起来？笔者认为，教师首先得“童化”学材，顺应儿童的思维发展特点，这样才能让规律探究课堂鲜活起来。学生的课堂学习离不开合适“学材”的支持和给养，教师要对“学材”进行“童化”处理，为学生的学习与成长提供更多的“源泉活水”。

【“间隔排列”的教学片段】

游戏引入：同学们，石头剪子布的游戏玩过吗？来和电脑老师玩一玩这个游戏吧！准备好了吗？（出示PPT有序出现石头、剪子、布）

采访学生：最后的几次你一直都是赢的，有什么心得吗？

学生回答：我发现里面是有规律的，一直都是石头、剪子、布、石头、剪子、布……这样出现的。

教师小结：确实，发现规律就能轻松取胜。这节课我们就来探索规律。

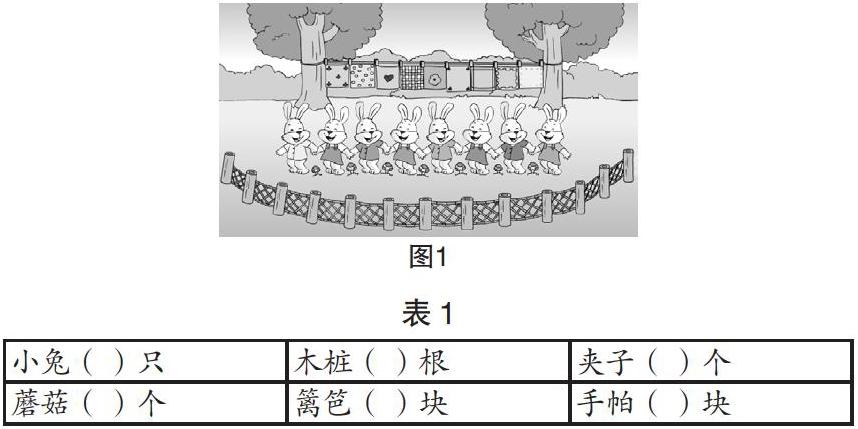
引入例题：快乐花园里的小兔子正在跳舞呢！仔细观察，兔子和蘑菇排列有什么特点？

生1：一只兔子一个蘑菇，一只兔子一个蘑菇地排下去的。

生2：每两只兔子之间有一个蘑菇。

教师回应：他们说得对吗？我们一起来验证一下。

继续观察：木桩和篱笆、夹子和手帕，它们的排列有什么特点？

（同桌互说，再次感悟物体的排列方式）

整体观察：现在我们整体观察这三组物体，它们的排列有什么共同的特点？

学生回答：它们都是一个隔一个排列的。每两个之间夹一个物体。

教师小结：像这样，两种物体一个隔一个排成一行叫作间隔排列。今天这节课我们就来学习间隔排列。（板书课题）

【“简单的周期”的教学片段】

猜一猜的小游戏

课件出示：红、蓝、黃、红、蓝、黄

教师提问：你知道接下来老师会摆哪些颜色吗？你又是怎么知道的？

学生争先恐后，跃跃欲试：“红色！它们都是红黄蓝、红黄蓝这样排下去的！”

教师相机一组一组地圈出来，3个一组，每组都是红黄蓝。

教师鼓励：“你们观察得可真仔细！关注到了它们的排列规律。还想玩这样的游戏吗？”

学生大声说：“想玩！”

教师：“下面老师来唱一首歌，同学们仔细听：祝你生日快乐，祝你生日快乐，祝你生日快乐……同学们猜一猜，接下来老师会唱什么？”

全班学生不约而同地唱起：“祝你生日快乐！”

……

以上两个教学片段，都是通过游戏引入，再通过“童化”学材，引导学生观察和思考排列中的规律，让学生主动感知事物的排列规律，探究排列的规律。这样的设计顺应了儿童的思维发展特点，大大提高规律探究的效果。

二、儿童优先，聚焦“找”规律的方法

“儿童优先”不是“儿童中心论”，“儿童优先”包含着儿童能自主学习，教师绝不过多干预甚至“包办”等丰富内涵。儿童是学习的主体，是“真学”的发生者、行动者和受益者。“儿童优先”是指把儿童、儿童的学习力和生长力、儿童的真性成长等放在十分重要的位置，努力达到“教是为了不教，学是为了会学”的理想境地[1]。

【“间隔排列”的教学片段】

教师提供研究单（见表1），让学生根据图1自主探究并完成表1的填写。

活动要求： （1）数一数，填一填;（2）比较每组两种物体的数量，你有什么发现;（3）和同桌交流你的发现。

组织交流：第一层次为收“数据”，确保数据填写准确;第二层次为收“发现”，聚焦数量上的规律。

引导思考：比较每组两种物体的数量，你有什么发现？

生1：上面的比下面的多1，下面的比上面的少1。

生2：兔子比蘑菇多1，蘑菇比兔子少1。

生3：木桩比篱笆多1，篱笆比木桩少1。

生4：夹子比手帕多1，手帕比木桩少1。

教师小结：确实，每排两种物体的数量相差1。（板书：数一数，数量相差1）

引发思考：为什么两种物体的数量会相差1呢？我们以兔子和蘑菇这幅图为例，为什么兔子比蘑菇多1呢？除了数，你还有什么方法来说明兔子比蘑菇多1？找到研究单上的兔子图，试一试。

学生自主探究后上台交流自己的方法（见图2、图3）。

教师小结：尽管同学们画的形式不一样，但都是把一只兔子和一个蘑菇对应起来，并看成一组，一组一组地圈画，最后发现还多了一只兔子。

【“和与积的奇偶性”的教学片段】

1.抛出问题，激发思考。

（1）出示：1+2+3+…+99的和是奇数还是偶数？

（2）追问：如果不计算，你能直接说出和是奇数还是偶数吗？面对这个复杂的问题，我们可以怎样思考呢？

（3）小结：可以从简单的情况入手，看看有什么规律。

2.简化问题，初步感受。

（1）问题：2个数相加的和是奇数还是偶数？自己写下3个两个非0的任意自然数相加的例子，求出它们的和，再看看和是奇数还是偶数。

（2）学生举例。

（3）交流、板书：将部分学生举的例子中和是偶数与奇数的分开。

（4）讨论：仔细观察这些例子，你有什么发现？与同桌交流。

（5）小结、板书：

明确：和是奇数或偶数与两个加数是奇数还是偶数有关系。

板书：偶数+偶数=偶数;奇数+奇数=偶数;奇数+偶数=奇数

3.深化认识，找出规律。

（1）谈话：刚才同学们通过找两个非0的自然数相加的和，发现了和的奇偶性与两个加数奇偶性之间的关系。那任意3个、4个、5个或5个以上非0自然数的和是奇数还是偶数呢？

（2）举例：任意选3个、4个、5个或5个以上不是0的自然数，写成两个连加算式，先算出和，再判断和是奇数还是偶数。

（3）交流、板书算式。

提问：仔细观察我们现在列举的连加算式，你觉得在什么情况下，和是奇数或是偶数？

点拨：判断和的奇偶性关键要看什么？数中奇数个数与和的奇偶性有什么样的关系？

（4）验证、小结。观察刚才自己举的例子，和我们的发现一样吗？

你能说说加数中奇数的个数与和的奇偶性之间的关系吗？

小结：几个非0自然数连加，加数中，奇数的个数是奇数，和是奇数;奇数的个数是偶数，和是偶数。

4.解决问题，回顾反思。

出示：1+2+3+…+99的和是奇数还是偶数？为什么？

回顾反思：遇到这个复杂问题时，你们是怎么思考的？

小结：遇到复杂的问题，可以从简单的问题入手，找出规律来解决。在找规律时，可以先举出一些例子，再通过观察、比较，找找有什么特点，从中发现规律。

與一般类型的课堂相比，规律探究课型呈现的数学知识更加复杂，所揭示的结论有条件限制，我们不妨通过一个核心问题引发学生思考，借助探究单自主探究，聚焦“找”规律的方法，让学生经历从特殊到一般、从具体到抽象、从简单到复杂的数学思维过程，积累探索规律的相关经验。

三、情智和谐，玉成学生一生“童真”

“情”指儿童的个性品质，它包括情感、兴趣、态度、需求等;“智”指智慧和潜能，即儿童的言语智能、数理逻辑智能、肢体智能、欣赏智能、内省智能等。

以“规律探究课型”的教学为例，这里的“情”既可以是外在的情感激发，又可以是内在的探究需求激发。外在的情感激发，可以通过儿童化的语言、儿童化的情境导入等挖掘学生的情感需求，激发学生的学习兴趣;内在的探究需求激发，可以通过数学独有的思维之美，设计有层次、有节奏的探究活动，激发学生的探究欲望，使学生体会到成功的喜悦。所以，教师应从内外两方面出发，坚守儿童立场，实现情智共生、互进共融，玉成学生一生“童真”。

【参考文献】

毛梦雪.小学数学“探索规律”的教学价值与策略[J].试题与研究，2020（11）：57.