桥梁静载试验优化设计算法的改进及应用研究

杨美云 许康曦 詹航

作者简介：

杨美云（1988—），工程师，工学硕士，主要从事桥梁工程设计工作;

许康曦（1989—），工程师，工学硕士，主要从事桥梁及市政工程相关结构设计工作;

詹 航（1990—），硕士，主要从事桥梁设计工作。

研究发现，运用常规的离散变量复合形法，虽然能求解多变量有约束的桥梁静载试验优化布置问题，但是当约束变量较多时，用复合形求解车辆布置问题，容易陷入“死循环”，难以收敛到最优解。为此，文章对离散变量复合形法做了适当的改进，以提高离散复合形法在布载试验中的运算效率。

荷载试验;优化设计;离散变量;改进复合形法

U442A381303

0 引言

笔者近几年在桥梁荷载试验优化设计中，投入了大量的研究精力，从最初的连续变量复合形法研究，转换到离散变量复合形法研究[1-3]。以加载效率及试验所需最少车辆数为目标函数，车辆行驶方向、车道数、布置间距、车辆类型为设计变量的优化数学模型[1]，在桥梁荷载试验中的应用，取得了很大发展。虽然采用了离散变量复合形法取得了一定进展，但是由于设计变量繁多，有离散型和连续型的设计变量，运行过程中仍然存在一些局限性的问题，如运行过程中经常搜索进入局部“死循环”，需要人为强行结束运算，或手动调整运算过程，运行时间相对较长。为了解决离散复合形法在荷载试验中运算的缺陷，本文对离散变量复合形算法进行了适当的改进。

1 离散复合形法改进

离散变量的主要步骤为，拟定初始离散点，产生初始复合形，计算目标函数，进而离散一维搜索，择优得出最优解。若此过程不能收敛，需循环重复运算。当搜索到不好的点时，调优运算将耗费大量的时间，或陷入“死循环”。本文以离散变量复合形法为核心，在不改变复合形本质算法的条件下，通过改进初始点、改进迭代终止条件、配合二次加速措施[4]，从这三方面去干预、改善复合形法在荷载试验中车辆布置优化的稳定性及收敛性。

1.1 改进初始点

桥梁荷载试验中的优化效率最优问题，属于多变量的离散约束问题，需要在以车道数、车辆行驶方向、车辆数、车辆位置、车辆类型等多个离散点中选定一个初始点进行复合

形法运算。随机选用的初始离散点不一定都能满足约束条件，在计算过程中，容易进入“死循环”。

此时，最有效的方法是，增加初始点的约束条件。在初始点，初始变量的可行域内，只有能保证试验加载效率达到0.85以上的离散点，才能作为离散复合形的初始点，并进入下一步的运算。

1.2 改进迭代终止条件

根据荷载试验中的离散复合形法的终止条件，即加载的目标函数见式（1）：

minf（x）=r1∑zi=1Li+100·（η0-1.0）2 （1）

约束条件见式（2）：

|η|≤1.05;x1，i-1-（x1，i-1+CarLengthi-1）≥5（2）

可知，当迭代中加载效率值、加载车辆位置不大于给定的离散增量时，即可完成运算。

虽然满足了约束条件，但是不能保证所用车辆数最少，目标函数最小。因为运算还未搜索到最优解，就已经进入局部最优解中停止了计算。为解决这一缺陷，可结合实际人为地增加程序迭代次数[5]，把满足终止要求的离散复合形点，再次循环迭代替换初始顶点进行计算。

1.3 二次加速措施

以上改进措施，主要是使调优运算不断运行下去，但是不能保证运算终止的效率。故此，再次引入二次加速措施，以便提高运算效率。

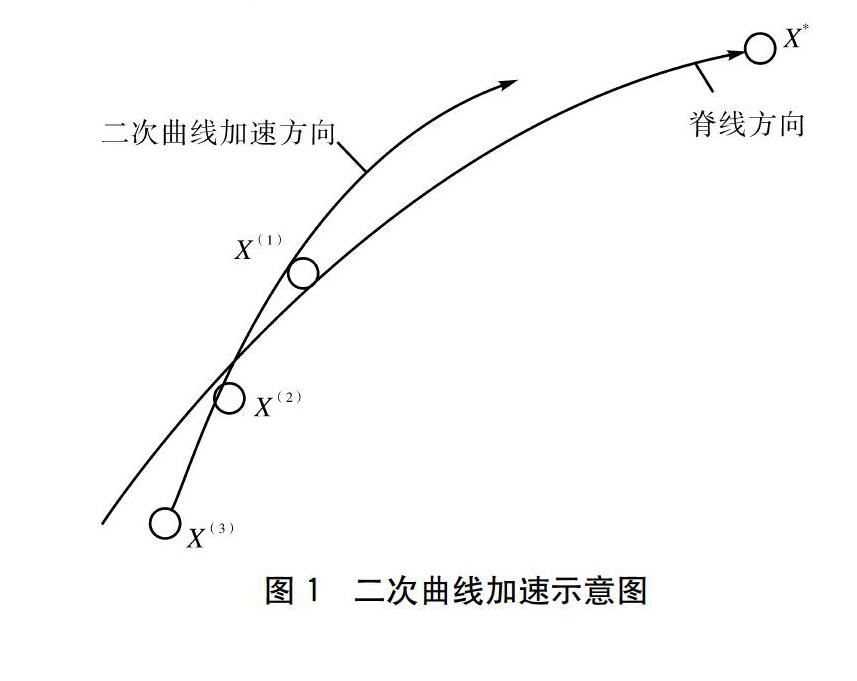
二次曲线加速措施是利用三点成线的原理进行离散一维搜索，选取最优的三个目标函数点，拟合一条曲线。在此曲线中，选取一个单调有规律性的变量，即约束条件作为自变量，其他约束条件作为因变量，沿此自变量的方向上进行搜索，产生新的最优离散点，大大加快运算速度。

二次曲线拟合的原则是选取复合形中三个最好的顶点X（1）、X（2）、X（3）这三个点须同时具备目标函数F（X（1））X（2）k>X（3）k的单调性条件。在此三个点确定的二次曲线方向上进行离散一维搜索，搜索出新的离散点Xi ;二次曲线加速成功的标志是新产生的离散点Xi<最好点。此时，可用新点替换最好点进入下一轮运算。若是沿选用的二次曲线方向上搜索不到满足条件的新点代替最好點，此种情况下，需要调整二次曲线的搜索方向，改选其他分变量作为自变量，再次选择三个具有单调性的点进行二次曲线加速运算。

2 算例对比分析

为验证改进复合形法的有效性，在梁片数、桥梁跨径结构形式不变的情况下，笔者继续以同一算例20 m跨简支梁预应力混凝土T梁桥为计算实例，对改进的算法进行验证分析。

主梁立面及标准横断面图，见图2、图3。

桥梁荷载按公路-Ⅰ级设计，主梁翼缘板采用刚性连接的连接方式。主梁采用C40混凝土，弹性模量E=3.25×1010 N/m2，跨中截面的惯矩为Ic=0.066 26 m4，结构基频为f1=4.187 Hz，结构的冲击系数为μ=1.262。此处以边主梁作为试验的加载研究对象，应用Midas有限元程序建立边主梁单跨有限元模型，选取3个具有代表性的主桥静力加载控制截面位置，进行加载分析，即剪力最不利位置的支点截面J1，1/4跨径处截面弯矩最不利位置J2，跨中截面弯矩、挠度最不利处J3。具体位置见下页图4。

在三个加载工况下，分别给定复合形法的初始参数值，初步拟定试验所需车排数;桥梁左右延伸一定长度;设计车道数;复合形顶点个数k=n+1=4·nc+1=4×5+1=21;离散一维搜索步长α=1.3;终止系数：EN=k-1=21-1=20。根据这一系列初始值[1]，然后进行复合形法迭代运算，最终得到改进后各工况最优解及布置情况。改进后复合形算法的计算结果与未改进前的计算结果对比情况如表1所示。

由表1对比可知，改进后的荷载试验在相同加载条件，保证效率指标都满足要求的情况下，所用的运行时间均比未改进前要快，且改进后的算法，使得荷载试验程序的运行更稳定，能保证程序启动后一次就运行到底，中途不会出现“死循环”和需要人为强制后台终止运算的现象发生。

3 结语

本文通过对常规离散复合形法的改进，提高了离散复合形法在桥梁荷载试验中的运算效率和局部搜索能力的稳定性。同时，通过算例对比分析验证了增加改进措施后的离散复合形法，在桥梁静载试验优化设计中的适用性更高。

[1]王小松，杨美云，陈 斌.基于复合形法的荷载试验车辆布置优化设计[J].重庆交通大学学报（自然科学版），2014，33（6）：18-21.

[2]杨美云，陈生华.离散变量复合形法荷载试验优化设计研究[J].西部交通科技，2015（4）：66-69.

[3]杨美云.桥梁静载试验加载方法研究综述[J].科技创新与应用，2013（23）：208.

[4]朱伯芳，黎展眉，张璧城.结构优化设计原理与应用[M].北京：水利电力出版社，1984.

[5]张火明，陆萍蓝，吴剑国.离散复合形法的改进及应用研究[J].中国计量学院学报，2006（12）：300-304.