基于AHP-熵权法的中小微企业信贷决策模糊综合评价

刘景琦 王 蕊 孙明浩 荣凤芝

一、引言

中小微企业是促进实体经济、稳定就业以及鼓励创业的重要力量，在经济社会发展、解决国计民生问题方面有着至关重要的作用。但是“融资难”问题一直制约着中小微企业发展；加之2020年以来新冠肺炎疫情冲击，本就经营规模小、抗压能力差的中小微企业面临着由于停工停产导致的营业收入“断崖式”下降以及资金链断裂等种种风险，因此银行针对中小微企业制定恰当的信贷策略具有很强的现实意义。但是就目前研究现状来看，大多数依然是基于理论层面提出一些对策建议，缺少必要的数据支持，并没有很强的可操作性，导致进行的研究结论可参考性和指导性不高。

本文通过123家中小微企业，选取一系列会影响银行信贷决定的指标，为银行做出相对应的信贷策略选择。

二、数据来源及研究假设

（一）数据来源

本文所用数据来源于“全国大学生数学建模竞赛”官网。

（二）研究假设

从银行角度出发，对中小微企业相关的信贷策略进行决策，我们选取了123家中小微企业并假定银行放贷的假设条件如下。

1.对确定要放贷企业的贷款额度为10万-100万元。

2.年利率为4%-15%；贷款期限为1年。

3.问题假设：①假设企业在附件给出的日期中可以正常存续以及在可预见的未来可以正常运营。②假设不考虑资金的时间价值。③假设企业名称及其销项税额发票中税率的众数反映其所从事的主营业务。④假设附件中所给出的企业均为中小微型企业，符合国家对于中小微企业的标准。

三、模型的建立与求解

（一）信贷策略评价体系的建立

在进行模型建立前，我们需要进行整体评价体系的确立，从而方便后续数据的处理以及一系列指标的选取，本文通过构建出下列指标评价体系对银行信贷策略进行探究（见图1）。

（二）指标的选取

确定具体指标如表1所示。

1.企业毛利

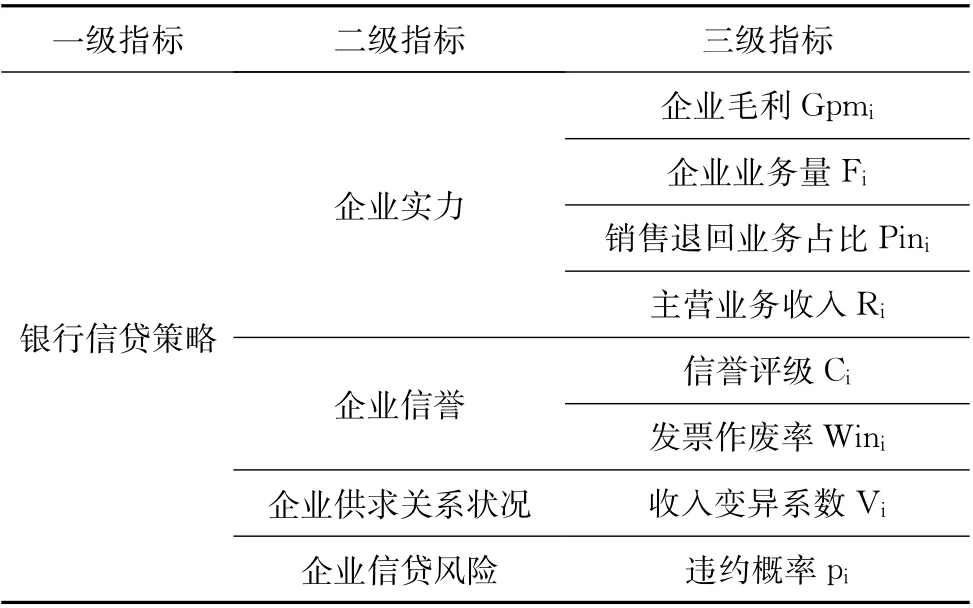
表1 分析处理指标

其中：Gpmi代表企业本月企业毛利；OutVati代表企业本月增值税销项发票中价税合计；InVati代表企业本月增值税进项发票中价税合计。

2.企业业务量。企业的规模以及实力也可以通过该企业月度的业务量进行衡量，即可以通过对附件中提出了作废发票以及负数发票后的企业销项税额发票进行计数，求得变量Fi。

3.销售退回业务占比

其中：Pini代表销售退回业务占比；In′i表示增值税销项税额发票中总的负数发票数；n1表示总的销项税额发票数量。

4.信誉评级。我们使用Python读写的Excel数据，根据不同的信誉评级A、C和D依据{A，B，C，D}→{100，80，60，40}的数据映射，对数据进行处理，记为Ci。

5.发票作废率

其中：Wini代表发票作废率；In″i表示增值税进项税额发票中总的作废发票数；n2表示总的进项税额的发票数量。

6.企业主营业务收入。销项发票指的是企业销售产品时为购货方开具的发票。企业实力可以用销项发票的规模进行表示，即可以用企业的月均销项税额对企业的主营业务收入Ri进行近似表示。

7.企业供求关系变异系数

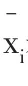
（三）数据的预处理

1.数据正向化处理

考虑到负数发票占比、违约概率、变异系数为极小型指标，因此需要对所有的指标进行正向化处理，将其转化为极大型指标，利用公式为：max－x进行正向化处理。

2.数据标准化处理

为消除不同指标量纲的影响，我们需要对已经正向化了的矩阵进行标准化处理，对于已经标准化了的矩阵Z中的每一个元素Zij，运用如下公式进行标准化。

（四）企业信贷风险的量化

1.Logit模型介绍

可以选择构建如下模型，当pi=0时可以看作企业没有发生违约的事件；但是当pi=1时就表明企业发生了违约事件。因此可以定义企业违约概率为pi，因此可以构建如下Logit回归模型：

在选取数据时，为最后对模型进行检验，选择其中前100组数据作为训练组，后23组数据作为检验组，对模型整体的拟合情况进行分析。

2.模型求解

首先利用Logit模型进行模型拟合，在此处选取训练组的100个样本数据，得出结果如下。

利用SPSS进行Logit模型构建，可求解出Logit回归模型：

同时，可以计算出企业违约概率为：

这样一来，就可以对每一个企业的信贷风险进行量化分析，对每一个企业违约风险都有一个具体概率值。

3.模型检验

（1）样本内检验。样本内检验指的是利用我们初始设立的训练组的数据，通过对比实际值与预测值进行检验，检验结果见表2。从中可以看出，对于实际没有违约的92个企业中，Logit模型全部预测正确；对于实际违约的8家企业中，把4家企业预测为没有违约。综上，对训练样本的初始分组案例的96%进行了正确分类。

（2）样本外检验。利用之前预留出的23个检验样本，继续进行样本外检验；此时仍将分类切割点的值定为0.5，预测值大于0.5即为违约，反之为正常值，检验结果见表3。从中可以看出，对于预留出的23组检验样本数据，该Logit进行了预测精度为100%的正确分类。

综上，使用Logit模型构建函数可以较为精确地对所给数据进行拟合和预测，因此可以利用式（7）求出每一个企业的违约概率p，来对企业的信贷风险进行量化处理。

（五）构建模糊综合评价模型

在对公司信贷风险进行量化后，接下来应综合企业的供求关系以及实力对每一个公司进行综合评价，根据评价结果进行决策实施。

首先选取上述指标作为模型的输入变量，即为因素集U1={u1，u2，u3}，即分别为企业实力、违约概率以及收入变异系数；其中企业实力U2={u′1，u′2，u′3，u′4}，分别代表企业毛利、企业月均销货次数、负数发票占比以及主营业务收入。需要建立一个如图2所示的二级模糊综合评价模型。

其次确定评语集为V={v1，v2}，分别代表银行选择贷款给该企业以及选择不贷款给该企业。最后根据附件中给出的经过上文处理后的数据，依靠模糊综合评价模型，根据每个企业基于v1的得分进行排序进而实施相关决策。

1.因素集的权重确定

（1）利用层次分析法（AHP）计算权重。①第一层权重的确立。综合利用算术平均法、几何平均法以及特征值法可以求得权重为ω1={ω1，ω2，ω3}={0.3，0.6，0.1}。②第二层权重的确立。根据第二层U2={u′1，u′2，u′3，u′4}也可以通过构建层次分析图，进而求取的权重为：0.48、0.16、0.12和0.24。

（2）利用熵权法计算权重。由于采取层次分析法（AHP）构成对比矩阵还是存在一些主观因素，因此我们想要利用熵权法来计算权重对第二层层次分析法求取的权重进行修正。通过Matlab可以很容易得出利用熵权法算出的第二层的权重分别为：

ω2={ω′1，ω′2，ω′3，ω′4}={0.5037，0.1556，0.145，0.2671}

根据以上层次分析法求得的权重，与用熵权法求得的权重取算术平均可得：

ω2={ω′1，ω′2，ω′3，ω′4}={0.4919，0.1578，0.145，0.2536}

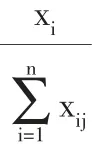
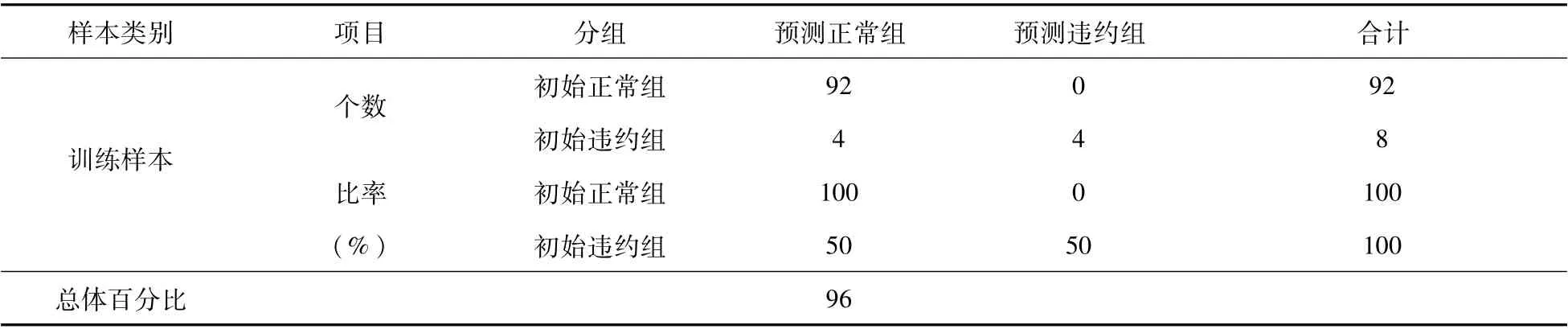
表2 训练样本内检验结果

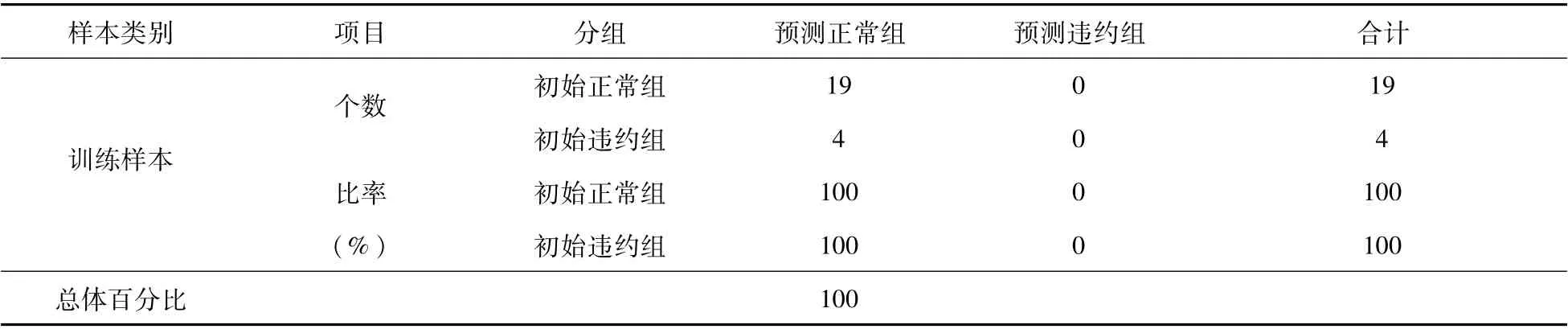
表3 检验样本外检验结果

上文已经求得了ω2={ω′1，ω′2，ω′3，ω′4}。故算出综合评判为：B1=ω2·R2。

（4）综合评判。如果有一个从U到V的模糊关系R=（rij）n×m，那么就可以利用R得到下面的模糊变换：

TR：F（U）→F（V）

由此进行变换，就可以得到综合评判的结果B=ω1·R1；其

可以求得各企业的得分如图3所示。

因信誉评级为D的企业原则上不予放贷，因此我们把评级为D的企业进行剔除，将剩余企业的综合评价得分进行算术平均，以此平均分作为阈值，大于此平均分的企业银行应选择贷款，而低于此阈值的企业银行应选择不予放贷。依照上述原则，筛选出了应予贷款的67家企业。

2.信贷策略的决定

随着企业制定利率的高低，其客户流失率会发生一定变化，为考虑企业预期收益最大化，我们建立如下目标函数：

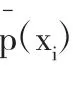
（1）客户流失率曲线的拟合。我们运用Matlab中的cftool工具箱，对不同等级的客户流失率及与客户关系进行拟合：为了避免过度拟合问题以及尽可能做到残差平方和（SSE）最小，我们选取多项式形式对数据进行拟合，并且最高次幂（degree）设为3；拟合出的函数如下：

此时，被解释变量对于系数是线性的，可以用判定系数R2来对模型的拟合优度进行判别，R2＝0.9977，拟合优度良好，且未出现过度拟合的问题；拟合出的函数图像如图4所示。

（2）穷举择优算法的进行。在进行了信贷决策后，我们应对这29家企业进行贷款额度以及利率的制定。我们使用C++语言，利用穷举择优算法，依托以下条件，对固定年度信贷总额下的最优信贷策略进行求解：

根据实验结果我们得出，当C取990-1 000之间的数字时，企业2020年的预期收益、对于不同市场的分配金额以及利率是趋于稳定的，即在此区间内应按照相应的金额、利率对不同市场进行分配，同时各个市场内部可以按照上文中模糊综合评价的得分进行内部分配。

四、模型的评价与改进

（一）模型的优点

1.模型较为简洁，将银行是否放贷的决策问题转化为一个模糊综合评价类问题，并且利用层次分析法与熵权法结合的方法求取权重，避免了采用单一的办法所造成的偏差，求得的权重也可以做到更全面更有效。

2.数据处理以及模型求解时充分运用了Python、Matlab、C++、Lindo和SPSS等编程、统计软件，比较好地解决了问题，获得了较为合理的结果。

3.建立的模型准确度高。

4.模型的建立以及应用较简单，具有一定的普适性。

（二）模型的缺点

1.受所收集数据约束，有一部分指标并没有考虑进去。

2.阈值的确定较为主观。

3.选取的指标之间具有一定相关性，显得模型比较冗余。

（三）模型的改进与推广

1.模型的改进

（1）可以考虑更多财务指标如资产负债率、销售毛利率等，来对模型进行改进。

（2）衡量企业是否违约后续应以企业是否被标记为“ST”进行判别。

（3）在各信誉标准内部设立综合评价体系，对于贷款额度作进一步细分。

2.模型的推广

本文的模型普适性较强，可以用于企业信贷风险的评估和各大行业对于不同企业实力的判断，以及对应策略的制定，也可以帮助银行或企业面对突发因素时做出科学应对。