基于遗传—退火混合算法的油藏动态优化研究
冯高城 马良帅 姚为英
中海油能源发展股份有限公司工程技术分公司, 天津 300450
0 前言
海上油田中高含水期面临着油水分布复杂、剩余油挖潜难度大、开发中后期生产调整困难等问题,直接导致油田稳产困难、开发成本逐年增加[1-2]。针对油田持续稳产与优化降本等问题,油藏生产优化是一种较为可行的技术手段。即通过调整油井产出和水井注入状态实现油藏生产效益的最大化。国内郎兆新最先提出油藏最优控制优化开始,直到张凯等通过将最优控制模型与油藏生产优化相结合,才真正意义上形成了油藏生产的动态优化理论,并在聂建英的深化研究中,逐步实现了最优控制理论在闭环油藏管理中的应用[3]。
智能油藏优化技术在国内经历了近30年探索,现代油藏生产优化已取得长足发展与关键性突破。油藏动态实时优化关键问题则是在有限时间内寻找到全局最优。现代智能优化算法[3]主要包括禁忌搜索算法、遗传算法、蚁群优化算法、人工神经网络算法等,可以通过数学抽象模型利用算法求解全局最优值。同时,油藏优化算法寻优过程中的梯度求解,目前主要应用SPSA和EnOpt算法等无梯度算法,通过估算优化变量与目标函数的敏感性或相关关系获得近似梯度或概率梯度进行优化[4],该梯度能够最佳逼近于真实梯度,每个迭代步只需若干次目标函数值计算,效率较高、应用方便。但目前遗传算法等现代优化方法在复杂多项式[5]优化求解过程中,计算解集易陷于局部解或者折中解,无法做到局部搜索与全局最优的互相兼容。
为此,基于油藏优化的NPV目标函数,改进以往SPSA与遗传算法(GA)相结合的优化算法[4],引入退火模拟算法(SG)提升局部寻优与全局寻优的兼容性,从而避免了优化方案过早陷入局部收敛的问题。在混合优化算法的控制下,持续迭代优化注采井生产制度,并与油藏数值模拟技术耦合,达到改善油田开发效果的目的。运用该方法对A油田开展油藏注采结构优化调整,取得了较好的应用效果。
1 最优控制数学模型
油藏优化生产最初将累采油或者最终采收率作为指标优化,但随着油田的开发,油田普遍进入中高含水期,注水成本及产出废水处理问题所带来的经济效益问题成为油藏生产优化新的关注点[6-10]。根据国内外研究,通过设置约束条件,基于分阶段调控油水井的生产参数,从而获取开发期间内经济效益最大[11]。现采用以下改进的经济目标函数来评价油田开发效果,将生产平台液处理费用、注水成本与转注成本进行单独考虑,表达式为:目标函数(NPV)=(油价×累产油-产水费用-注水费用-转注费用)-平台液处理费用。
因此,油藏生产优化的数学模型可以表述为:
(1)
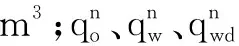
2 基于SG-AG的方法
对于油藏开发生产,通过对地下流体状态参数m的优化,实现经济目标函数M的最大值,并求取此时的优化控制变量u,获得最终的可行解x*。通过控制变量设置油藏整体规划、单井界限的上下限约束来对目标函数进行寻优。在寻优的过程中,既要保证在较短时间内获得可行解x*,也要避免陷入局部最优。GA最早由Holland依据达尔文进化论原理建立的一种全局最优化搜索算法,可以快速地搜索出解空间中全部解,克服了其他算法的快速下降陷阱问题,适应性好、鲁棒性强[12-13];SG是Metropolis最早借鉴固体金属退火的原理建立的一种全局最优化方法,是一种局部寻优搜索算法的扩展[14]。
通过给定油藏注采结构参数初始值,利用GA确定注采数据种群个数,获得初始化数学模型解集。将目标性能函数转化为适应度函数,通过适应度函数筛选出部分个体,通过一点概率选择部分个体进行杂交产生子代;再按照一定概率进行交叉变异,更新产生新的种群[14]。在产生制度扰动的同时,利用SG算法加强扰动规模避免局部搜索,以此确定搜索方向;而对于性能指标M(u,x)对控制变量u的梯度,则按照SPSA算法计算其平均梯度,迭代优化直至为0。最终通过算法调用油藏数值模拟器计算目标函数的最大净现值,见图1。
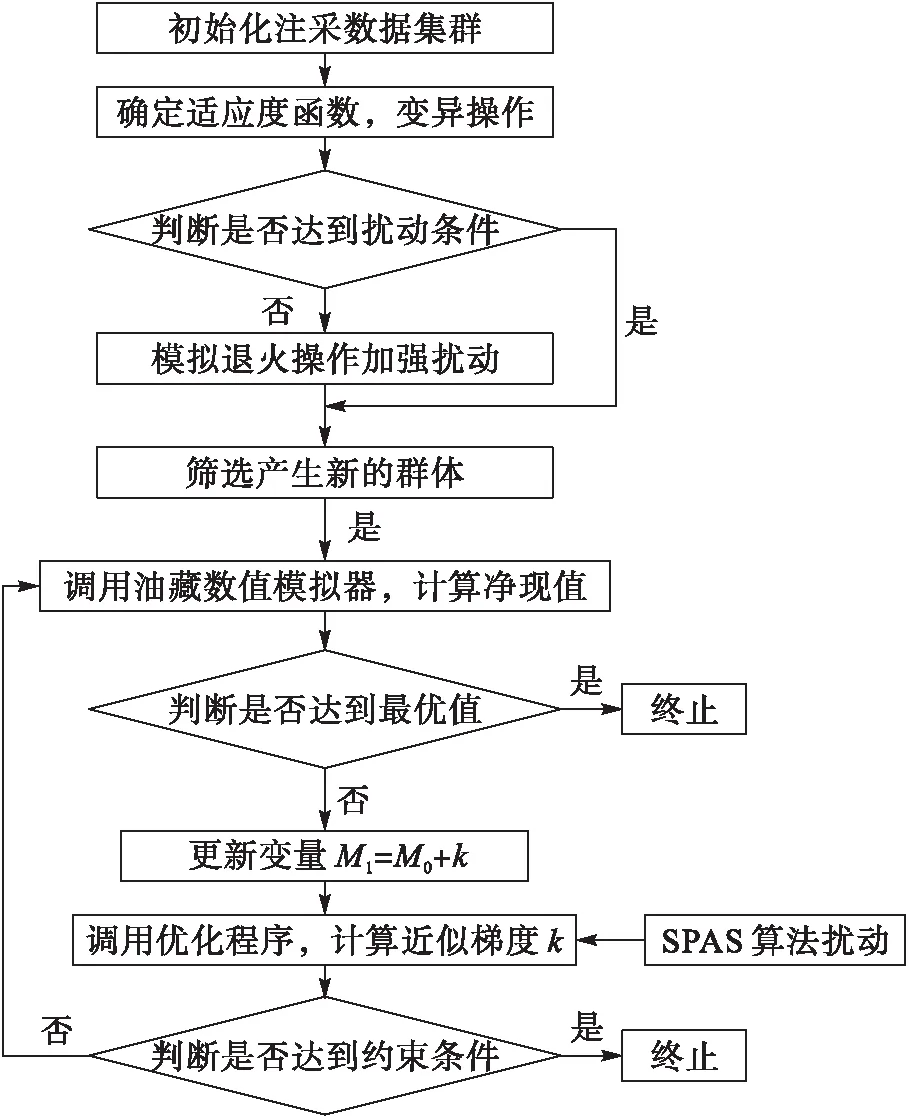
图1 SG-AG流程图Fig.1 Flowchart of SG-AG
2.1 基于SG-AG的优化方法
SG-AG方法基本思想是通过给定初始参数值,将遗传算法作为全局寻优的关联算子,通过选择、交叉、变异等遗传操作来产生一组新的个体,利用退火模拟操作加强对种群范围扰动,再对每个个体独立进行退火模拟操作,以其结果作为下一个群体中的个体反复迭代,直至满足终止条件。该思想的有益效果是通过遗传算法较强的全局搜索能力,以种群为搜索单位,通过退火模拟算法加强扰动提高局部搜索能力,保证全局最优的同时避免由于遗传算法陷入局部最优[14]。SG-AG优化油藏生产制度的可行解可通过以下步骤获取:
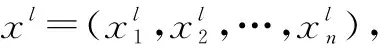
(2)
式中:t为当前迭代数;∂≥1常数。
2)对于油藏生产优化,首先根据目标函数M(u,x)按照遗传算法原则确定其适应函数m(x)=M(u,x)±J(x),其中J(x)为约束条件目标函数[15],当目标函数求取极小值时取“+”号,求极大值时取“-”号。油藏优化问题属于求取极大值问题,则适用函数为m(x)=M(u,x)-J(x)。
3)按照适用函数m(x)计算各注采井对应的适用度函数,通过对适用度大小进行排序,针对油藏目标函数寻优极大值问题,将适用度按照升序排列。则群体内各个个体被选中的概率为:
(3)
式中:q为最优个体的概率,范围0~0.1;R为排序后的序号;r为种群大小。
4)在此基础上,对种群内任意两个个体XA、XB进行交叉计算,交叉计算后的新个体为:
(4)
式中:γ=e(-αT/t);α为非均匀算数交叉系数;T为当前最大迭代数;t为当前迭代数。
(5)
式中:l为编码个数;∂为(0,1)之间的均匀分布随机数。
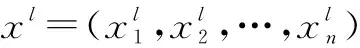
(6)
计算新点的评价函数值f(x′)及函数差Δf=f(x′)-f(x0);若函数差Δf≤0,则接受新点x′为当前解,若函数差Δf> 0,则以概率p(f)=e(-f/KT)接受新点作为新的当前解,其中k为波兹曼常数。T0为初始制度,T0逐渐减少,当T0趋向于0时,重复本步。
6)计算动态交叉率与变异率保证遗传算法在过程中朝着最优方向计算,计算方法如下:
(7)
式中:F为个体平均适应度;υ1、υ2、μ1、μ2为参数变量;Fmin为最小适应度;F′为较小适应度;pj为动态效率;pb为动态变异率。
2.2 SPSA无梯度寻优算法
根据最优化原理,油藏依据目标函数M(u,x)按照寻优方向进行搜索,下面需要解决其搜索步长的问题。沿着性能指标函数对u的梯度方向进行迭代搜索计算,便可求得指标函数的局部极大值及相应的最优控制u。对最优控制u的搜索梯度方向,则基于离散极大值原理,采用随机扰动近似方法来估算目标函数的梯度,该方法主要是通过对所有控制变量进行同步扰动计算来获得梯度[16-18]。再通过SPSA梯度法解决其它约束条件[19-22],目标函数在u位置的近似梯度为:
(8)
其中对控制变量u的迭代方程为:
(9)
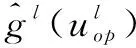
在实际油藏优化过程中,其搜索梯度是在不断变化的,上升与下降方向均存在,在此采用平均值作为新的搜索方向,不断迭代计算控制变量的梯度值,直至趋向于0,中止计算,此时变为最优值。基于此平均梯度计算目标函数的数学期望[15,22]:
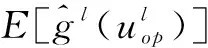
(10)
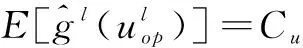
(11)
式中:E[ ]为数学期望;Cu为协方差距阵;Zl为标准正态分布下的随机扰动向量。
通过计算控制变量u处扰动向量的梯度值,指导目标函数对控制变量的梯度值接近于0时终止计算。综上,遗传算法在寻找全局最优解的过程中采用随机概率的方式往往会陷入局部搜索或者早熟的情况,通过退火模拟的较强局部搜索能力,能有效解决油藏生产寻优方向问题。结合基于SPSA算法的无梯度优化确定梯度搜索方向,直至目标函数经济效益最大为止。下面将通过实际油藏对该方法有效性进行验证。
3 计算实例
以A油田为例,该油田构造为东高西低的低幅度背斜构造,北部有两条平行走向的断层组,断层间有边水供应。储层非均质性较强,平均孔隙度18%,渗透率400×10-3~800×10-3μm2,无效水产出明显。截至目前,投产生产井15口,日产油2 900 m3/d,平均单井日产油195 m3/d,累产油117×104m3。经过多年的连续开采,剩余油分布复杂,且北部和西部的弱边水水体能量有限,难以有效满足油田上产所需要的持续压力供给,亟待注水补充能量优化注采关系,实现油田经济稳产开发的目标。
为此,针对转注的4口井B5、B15、B18、B19,根据目前油藏的井网部署,优化该油藏注水井注入量及生产井产液量,从而形成主要对比方案如下:优化方案为4口转注井、11口生产井及生产制度优化;基础方案为4口井转注井、11口生产井持续原制度。
优化前各注采井注水量与产液量维持当前工作制度,此次优化过程初步考虑海上油藏及单井开发的注采边界约束,其中,油价按照2 779.39元/m3,污水处理成本为2.5元/m3,注水成本为4.9元/m3,注水量注入范围为5 000~18 800 m3,产液量产出范围为1 800~4 000 m3。默认设置其种群大小为2,优化步长设置为30 d,优化时长设置为180 d。优化前后剩余油分布对比见图2。
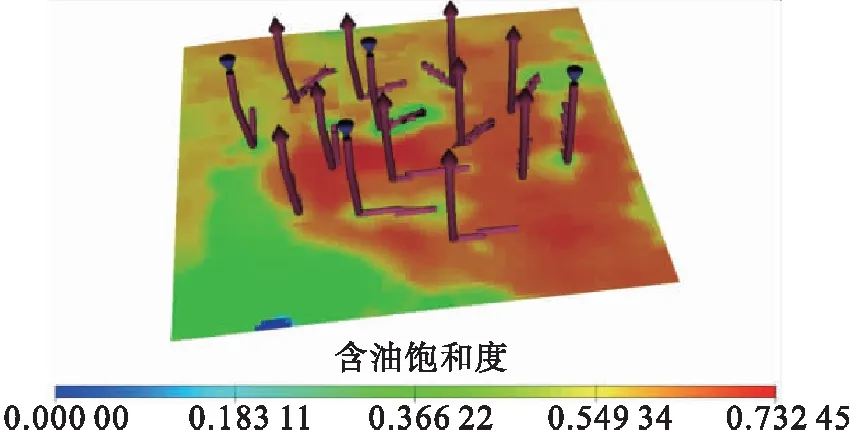
a)优化前末时刻剩余油饱和度分布a)Remaining oil saturation distribution before optimization
方案对比表明:优化后方案其含水上升率较低,综合递减率较未优化方案降低2.3%,累产油达到59.95×104m3;优化后方案较未优化方案日增油提高135.6 m3/d、日注水量减少1 700 m3/d、累产油提高约1.9×104m3。由此可见,优化方案较原始方案明显提升,同时表明该油田及时转注符合目前的开发需求、且越早优化效果越佳,见表1。
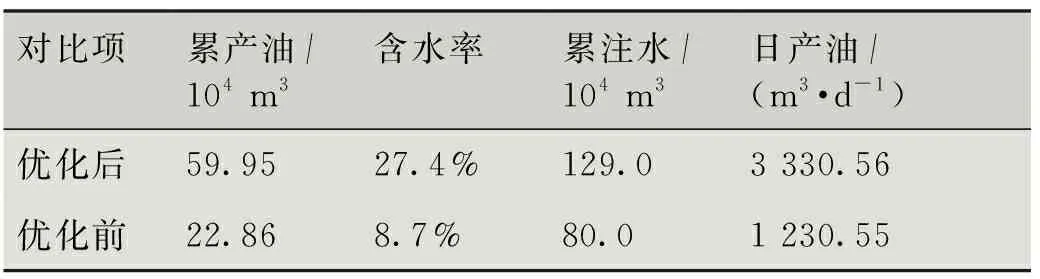
表1 优化前后方案结果对比表
预测结果显示,优化后方案从含水界限点开始转注,其水驱开发效果更好,见图3。优化前后方案对比结果显示,当迭代次数达到100时间步时净现值达到最大32万元,见图4。
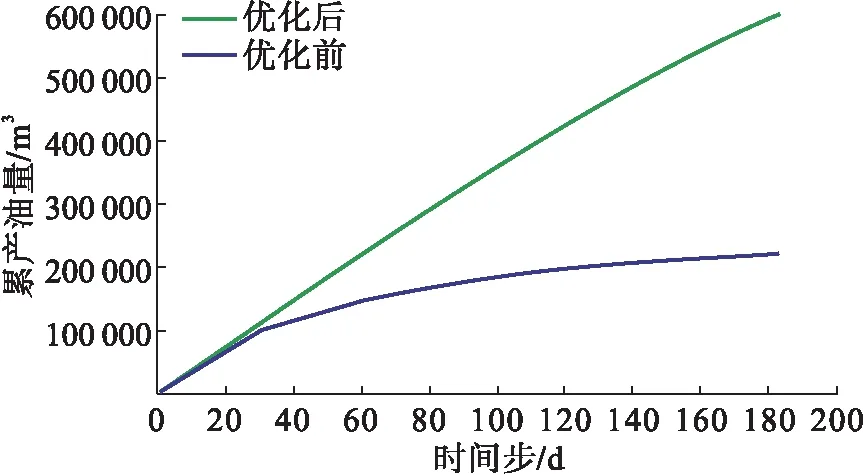
图3 优化前后各指标对比图Fig.3 Comparison of indicators before and after optimization
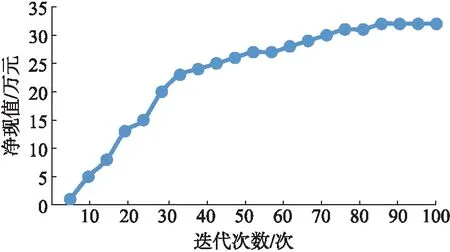
图4 优化过程中的迭代净现值图Fig.4 Iteration net present value during optimization
4 结论
1)基于SG-AG混合寻优算法,充分利用SG较强的局部搜索能力和AG的全局寻优能力,将SG作为一个扰动因子融入AG中,通过其算法的互补性有效地解决了寻优过程中由于过早收敛而导致的局部最优问题。通过SPSA算法调用油藏数值模拟器计算近似梯度,确定油藏目标函数净现值,可用于油藏生产优化寻优计算。
2)优化后最优控制方案综合递减率较未优化方案综合递减率降低2.3%,累产油提高约1.9×104m3、日增油提高135.6 m3/d、日注水量减少1 700 m3/d,有效提高了油田水驱波及效率,说明了油藏生产优化的必要性。

