太阳光谱地基跟踪遥感系统光学设计
胡 凯,徐 亮,杨伟锋,曲立国,金 岭,成潇潇,沈先春,王钰豪,刘建国,刘文清
(1中国科学院合肥物质科学研究院安徽光学精密机械研究所环境光学与技术重点实验室,安徽 合肥 230031;2中国科学技术大学,安徽 合肥 230026)
0 引言
太阳辐射是地球上一切活动的主要能量来源,其发射的电磁辐射在地球大气上界随波长的分布叫做太阳光谱,通过大气对太阳光谱变化的反应,可以确定大气结构、地表温度等信息,其也是一种有效的遥测整层大气中污染气体含量的方法[1−3]。以太阳直射光作为光源,通过测量和分析太阳光经过大气层后的吸收光谱来确定气体成分并反演气体浓度的太阳掩星通量(SOF)方法是一种新兴的测量气体排放率的方法,其基于利用与太阳追踪器相连接的傅里叶变换红外(FTIR)光谱仪记录太阳的宽带红外光谱,此系统可进行定点观测、车载走航观测、机载观测;能够做到对某一较大区域内污染气体的排放及分布状况进行实时、快速的监测[4−6]。研究表明:太阳追踪器的设计对于该类系统的使用范围、安装调试和性能都有很大的影响[7]。2005年,Kihlman等[8]为了使SOF方法更有效,开发了一种新的主动太阳跟踪器,其主要由上下两个反射镜及位置探测器组成,该追踪器存在的问题是:当太阳的高度角较高时,下反射镜无法将太阳光反射到上反射镜,从而无法在低纬度地区使用;且太阳位置变化时,经过上下反射镜后进入光谱仪中太阳光的光通量也在变化,无法保证光谱的信噪比一致。2011年,Gisi等[9]为了将太阳直射光的辐射非常精确地耦合到FTIR光谱仪中,设计了一个基于摄像头的太阳跟踪器,这种方式的跟踪需要图像处理算法进行反馈调节,会增加控制回路时间,不适于移动平台上的高精度跟踪。
本文提出了一种太阳跟踪系统,由两个相对于垂直方向保持45°的椭圆面反射镜组成,利用小孔成像原理和光电式跟踪方法进行跟踪,并对该系统进行了光学建模分析。此结构有利于安装调试,提高了光通量的稳定性,适用于移动平台上的全方位、高精度跟踪,并且在中国区域都可以使用。结合太阳掩星方法和傅里叶变换红外光谱技术,设计了一套用于太阳光谱地基跟踪遥感的光学系统,最后对设计结果进行了分析和评价。
1 光学设计指标
基于SOF方法的系统通常由太阳跟踪系统和傅立叶变换红外光谱仪组成,具体的工作原理如图1所示。FTIR光谱仪的工作原理是由光源发出的光束经过一定的光学系统准直后,进入干涉仪变成干涉光束,再由探测器接收干涉的信号,之后再经过傅里叶变换的处理变成光谱图。其主要由红外光源、干涉仪、检测器、光阑以及各种红外光学元件等组成,光源覆盖的光波段和所用的红外光学元件的工作波段会限制FTIR光谱仪的工作范围。而所设计系统采用太阳为光源的被动遥测技术,不考虑光源工作波段限制的因素。系统选择在实际测量中使用较多的600~5000 cm−1的中红外波段,因此分束器选择适用范围为600~5000 cm−1的ZnSe分束器,检测器选择液氮冷却型的MCT探测器,光谱响应范围为600~6000 cm−1,有效探测面积为1 mm2。
在FTIR光谱仪中干涉仪是最核心的部件,分束器是干涉仪系统中的一部分,目前干涉仪的种类繁多,但都是基于经典迈克尔逊干涉仪的原理发展而来,所以此处选用的干涉仪结构为传统的迈克尔逊干涉仪,其中动镜和定镜均为平面反射镜,根据国内外类似干涉仪的设计经验[10],选择干涉仪的通光孔径为24 mm。分辨率是FTIR光谱仪中的重要参数之一,其不仅受动镜移动的最大距离的影响,还受进入干涉仪的准直光束发散角的影响,而分辨率与准直光束发散角的关系为[11]

式中:αmax为准直光束的最大发散角,Δν为分辨率,νmax为测量范围内的最大波数。高分辨的光谱可以有效区分物质的吸收,但也会降低信噪比,所以要根据实际需求进行选择,此处选择FTIR的分辨率为0.5 cm−1,由(1)式得出准直光束的最大发散角为10 mrad。
太阳跟踪系统主要用于跟踪太阳并收集太阳的直射光,在基于SOF方法测量污染气体时,为了应对高速行驶、车辆转弯、上下坡等情况,太阳跟踪系统需要一定的视场,通过对城市道路坡度的调查[12],其规定坡度不会超过12%,确定其视场角为10°。为了保证足够的光通量、提高光谱的信噪比,并考虑到整体系统的尺寸,太阳跟踪器的通光孔径选择为50 mm。
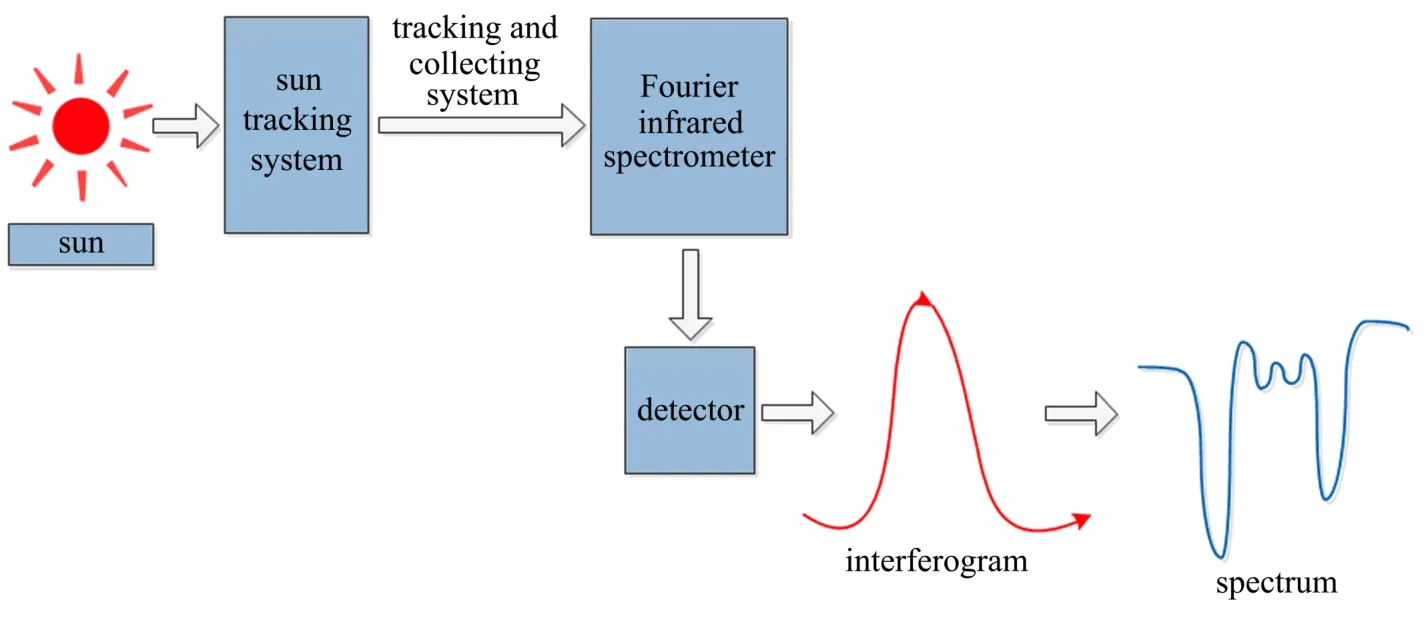
图1 基于SOF方法的系统原理图Fig.1 Principle diagram of the system based on SOF method
根据以上要求,确定太阳光谱地基跟踪遥感光学系统的主要技术指标如表1所示。
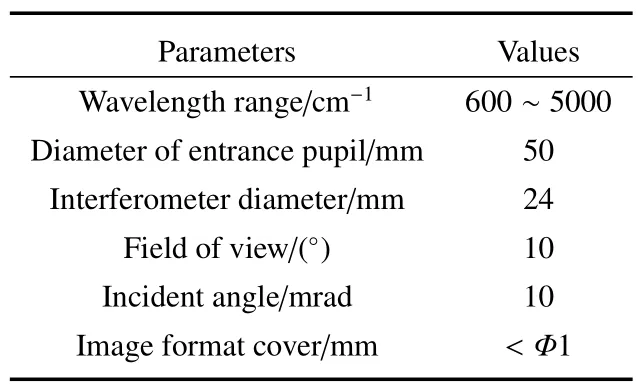
表1 太阳光谱地基跟踪遥感光学系统的主要指标Table 1 Specifications of solar spectrum ground-based tracking remote sensing optical system
2 太阳跟踪系统设计
太阳的跟踪方法一般分为两类,一类是基于反馈控制原理的闭环方法的主动跟踪,此类跟踪系统跟踪精度高;另一类是基于太阳天文坐标的开环方法的被动跟踪,此类跟踪系统无需使用反馈控制原理,但开环系统无法纠正任何错误,无法补偿系统中的干扰误差。根据太阳光谱地基跟踪遥感光学系统的应用要求,选择精度较高的闭环主动跟踪方式。对太阳的全方位跟踪可以通过一个高度角扫描镜和一个方位角扫描镜组合旋转的方式来实现,其光学结构如图2所示。其中高度角扫描镜和方位角扫描镜相对于垂直方向斜45°放置,高度角扫描镜可绕水平轴旋转360°,高度角扫描镜和方位角扫描镜可作为一个整体绕竖直轴旋转360°,从而实现对太阳全方位的跟踪;而且这种结构可以使经过该系统后的光通量保持稳定。具体跟踪的原理是利用小孔成像原理,在方位角扫描镜上开一个小孔,并在小孔后面放置一个光电探测器,太阳光经过高度角扫描镜反射后,再传输到方位角扫描镜,此时会在光电探测器上留下一个和小孔一样大小的光斑,根据光斑在光电探测器上的位置来判断太阳的实时位置,再通过反馈调节来跟踪太阳,此跟踪方式简洁方便,结构简单,只需根据探测光斑的偏移量来进行跟踪,减少了控制回路时间。
由太阳跟踪系统的视场角和通光孔径,计算出高度角扫描镜和方位角扫描镜均为长轴71 mm、短轴50 mm的椭圆平面反射镜,高度角扫描镜和方位角扫描镜的中心相距137.5 mm,小孔在方位角扫描镜的中心下方4.4 mm处。太阳跟踪系统中的光电探测器选择具有灵敏度高、测量精度高等特点的四象限位置探测器(PSD),其中心与小孔的中心同轴,尺寸为10 mm×10 mm。小孔直径的设计考虑到,光斑过大会降低PSD的探测灵敏度,过小会增加加工难度,并且会降低光斑强度,从而降低PSD的测量精度,所以选择直径为0.5 mm的小孔[13]。太阳跟踪系统的跟踪精度与PSD的精度、电机的控制精度等有关,假设其跟踪精度最低为ω,PSD与小孔的距离为dmm,则探测器所达到的最大视场角要满足

其测量精度也要达到dtan ω mm,所以在满足视场角的条件下d值越大,对PSD测量精度的要求就越低,从而电子学方面的要求和成本也就越低,因此设计选择d为28 mm。

图2 太阳跟踪系统的光路示意图Fig.2 Schematic diagram of optical path of the sun tracking system


设出射光线向量为k(x,y,z),根据反射定律可以得出反射矢量公式为

经过计算可以得出k的坐标表达式,进一步得出PSD上的太阳光斑轨迹方程为
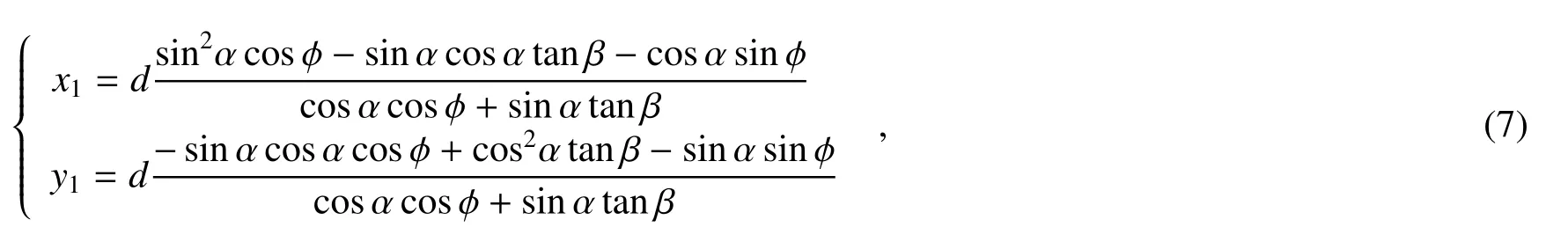
式中:x1和y1为探测器上的光斑坐标;d为PSD中心与小孔中心的距离,也就是28 mm。上述计算是假设太阳处于图3建立的坐标系x≥0的空间。如果太阳处在x≤0的空间,此时的光斑轨迹公式和(7)式一样,但太阳高度角β要替换成180°−β,上述计算的所有旋转角度的正负均符合右手螺旋法则。

图3 光斑轨迹的几何光路结构示意图Fig.3 Schematic diagram of the geometric optical path structure of optical spot track
从(7)式可以看出,当太阳跟踪系统绕着水平轴和垂直轴旋转时,PSD上的太阳光斑轨迹方程并不是简单的直线运动方程,为了更直观地分析,根据(7)式绘出其光斑轨迹,如图4、图5所示。图4是α=β且太阳高度角 β 分别为 0°、15°、30°、45°、60°、75°、89.9°时,以 φ 为自变量的图形,这种情况是太阳跟踪系统已对准太阳的高度角,然后只对太阳的方位角进行追踪。从该图形可以看出,光斑的移动轨迹相比于直线有一点弯曲,而且不是固定的方式,随着太阳高度角的增大,曲线以原点为中心,并从x轴开始逆时针旋转,旋转的角度等于高度角值;当β趋近于90°时,光斑的移动曲线也逐渐变成一个点。图5是 φ =0°且太阳高度角 β 分别为 0°、15°、30°、45°、60°、75°、90°时,以 α 为自变量的图形,这种情况是太阳跟踪系统已对准太阳的方位角,然后只对太阳的高度角进行追踪。从该图中可以看出,其与图4中的曲线形状及旋转趋势类似,但该图中的曲线是从y轴开始旋转。

图4 仅跟踪太阳方位角Fig.4 Tracking the solar azimuth angle only
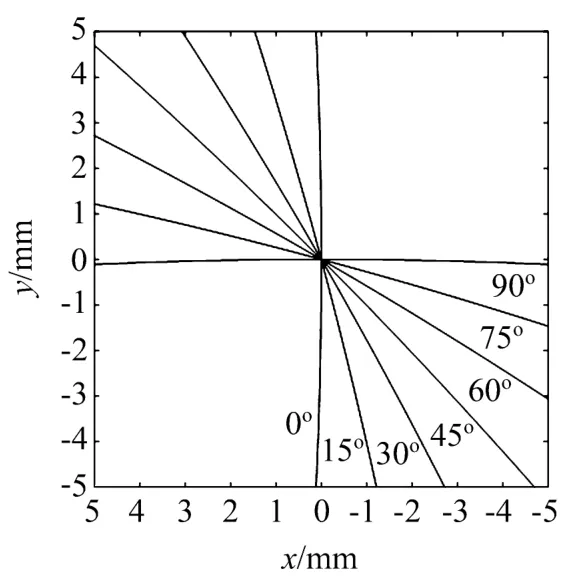
图5 仅跟踪太阳高度角Fig.5 Tracking the solar altitude angle only
通过比较两种情况下的光斑移动曲线,发现其近似于正交。上述推导的公式及曲线图对后面的控制系统如何更好地跟踪太阳具有重要的指导意义。
3 太阳光谱地基跟踪遥感光学系统设计
为了提高光通量,设计的太阳跟踪系统的通光孔径大于干涉仪系统的通光孔径,所以需要一个传输光路系统将太阳跟踪系统和干涉仪之间的光束进行很好地耦合。一般在干涉仪之前,会通过加上准直抛物镜并在其焦点上添加一个光阑的方式,将进入干涉仪的光束进行准直以减小其光束发散角。根据实际需要,且抛物镜的离轴角越大,准直性能越好,所提出设计在干涉仪系统之前选择一个口径为24 mm、焦距49 mm、离轴角90°的准直抛物镜。所提出的传输光路结构可以通过一个大口径的抛物镜1将经过太阳跟踪系统的太阳光先聚焦后再通过准直抛物镜进入干涉仪,如图6所示。当然还有其他方式,但由于反射镜越多,反射效率越低,所以要尽可能地减少反射镜的数量。为了将光束很好地耦合进准直抛物镜,本设计选择口径50 mm、焦距101.6 mm、离轴角90°的抛物镜1。光束经过干涉仪后会通过抛物镜2汇聚到MCT探测器上,其光路结构如图7所示,而MCT探测器的探测尺寸只有1 mm,所以汇聚的光斑的半径不能超过0.5 mm。

图6 传输系统光路图Fig.6 Optical path of transmission system

图7 迈克尔逊干涉仪的光路图Fig.7 Optical path of Michelson interferometer
根据离轴抛物镜的准直特性[15],可以知道具有相同入射角度的平行光束经过不同焦距的抛物镜聚焦后,其光斑的半径也会有差异。因此对所提出系统来说,在满足MCT探测器上光斑半径要求的情况下,抛物镜2的焦距越小,其入射光的最大倾斜角越大,光束允许的最大入射角也是太阳跟踪系统的最低跟踪精度,这一点根据前面设计的太阳跟踪系统的光路得出,从而对太阳跟踪系统的跟踪精度要求也会降低,并且根据(2)式,对PSD测量精度的要求同样会降低,使得整个系统的要求降低,从而降低整个系统的成本。相同条件下,不同焦距的抛物镜2对动镜倾斜的敏感程度不一样,如图8(a)、(b)所示入射光为10µm的单波长时,焦距为25.4 mm和152.4 mm的抛物镜2在动镜倾斜角度为0.1146°的情况下模拟得到的干涉条纹,由干涉条纹的形状变化可以看出,抛物镜2焦距越大,动镜倾斜造成的影响就越小,这可以提高系统的稳定性。

图8 抛物镜2焦距不同时的模拟干涉条纹。(a)25.4 mm;(b)152.4 mmFig.8 Simulated interference fringes when the focal length of the parabolic mirror 2 is different.(a)25.4 mm;(b)152.4 mm
为了平衡两者之间的关系,选择合适的焦距值,根据基于经典迈克尔逊干涉仪的FTIR光谱仪中的动镜最大倾斜角为41′′[16],在其他条件不变时,设置干涉仪中动镜的倾斜角度为41′′。然后利用光学软件中的ZPL宏使得抛物镜2的焦距值在10~100 mm范围进行变化,并观察焦距变化时模拟的干涉条纹形状和干涉图中的峰谷值,发现当焦距逐渐增大到52.5 mm时,其干涉条纹形状由弯曲逐渐变直(产生的图形过多,此处不便展示),其变化的趋势类似于图8(a)到图8(b)的变化。从峰谷值的变化也可以看出抛物镜2焦距值的大小对干涉条纹的影响。如图9和图10所示,焦距为52.5 mm时峰谷值减小为0.9641λ,并且在继续增大焦距后峰谷值保持不变,图10为焦距改变时的峰谷值变化曲线。最后综合考虑选择抛物镜2的焦距值为52.5 mm。

图9 抛物面镜2的焦距为52.5 mm时的干涉条纹Fig.9 Interference fringes when the focal length of the parabolic mirror 2 is 52.5 mm

图10 峰谷值曲线Fig.10 Peak to valley curve
本设计选择的上述三种抛物镜都是比较常见的类型,可以减少加工成本和时间。根据上述参数的计算,在Zemax中模拟进入干涉仪之前的光路结构图和太阳光谱地基跟踪遥感系统的总体光路结构图,如图11和图12所示。
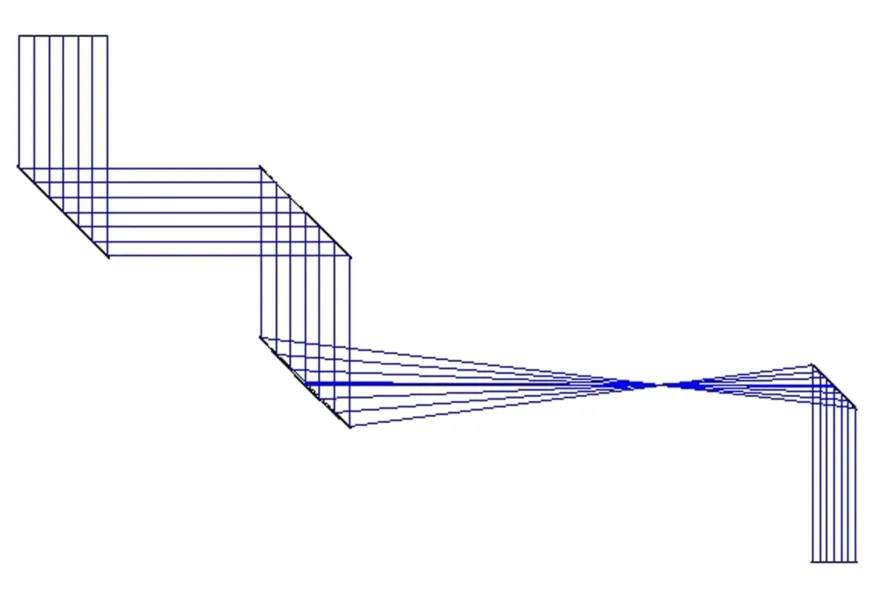
图11 进入干涉仪前的光路图Fig.11 Optical path diagram before entering the interferometer
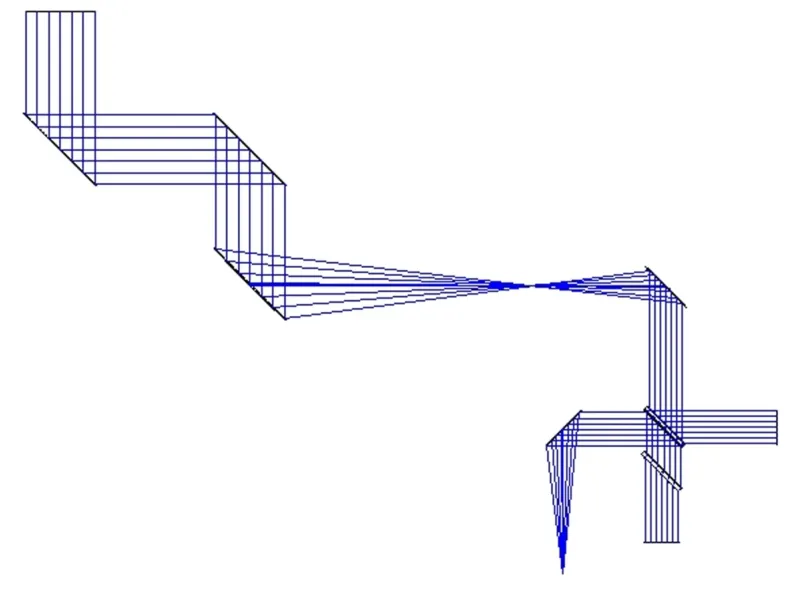
图12 系统整体光路Fig.12 Overall optical path of the system
为了确定入射光的最大倾斜角,从而对PSD的测量精度和系统的跟踪精度提出要求,有必要研究不同入射角下的平行光束经过干涉仪之前的光路后的准直光束发散角和经过整体系统光路的成像光斑的半径。为此设置不同的视场角,从图11光路结构中的最后一个面,观察在“Afocal image space”模式下的点列图,即准直光束的发散角;从图12结构中最后成像面点列图的几何半径观察成像光斑的半径。其结果如图13和图14所示,然后将结果记入表2。

图13 准直光束在不同入射角下的发散角Fig.13 Divergence angle of collimated beam at different incident angles

表2 入射角对准直光束发散角和成像光斑尺寸的影响Table 2 Effect of incident angle on divergence angle and imaging spot size of straight beam
由表2可以看出,入射角为0.118°的平行光束经过系统后汇聚的光斑半径为0.502 mm,进入干涉仪之前的光束发散角为4.24 mrad(小于10 mrad),而在满足准直光束发散角小于10 mrad时光束的入射角度最大为0.28°,但此时最后的成像光斑半径已经是1 mm,这会损失较大的光能量,降低信噪比,也会损失一些光信息。所以确定入射光的最大倾斜角为0.118°,进而可以得出太阳跟踪系统的跟踪精度不能低于0.118°,PSD的测量精度不能低于57.67µm,这为PSD的选型和验证系统的性能提供了依据。
4 太阳光谱初步观测
根据上述的仿真计算,设计了太阳光谱地基跟踪遥感系统的光机结构,如图15(a)所示,并搭建了实验平台,实物图如图15(b)所示[17],其主要包括220 V电源、FTIR光谱仪、太阳跟踪器、计算机、电路控制箱和GPS定位设备。图15(a)中的电机1直接和高度角扫描镜相连,从而带动其旋转,实现对太阳高度角的跟踪;电机2通过齿轮传动使得水平转台进行旋转,两个扫描镜固定在水平转台上,实现对太阳方位角的跟踪;为了可以实现更高的控制精度,两个电机都选择为伺服电机,其中PSD放置在暗盒中是为了减少杂散光的影响。

图15 (a)整个系统结构示意图;(b)实物图Fig.15 (a)Schematic diagram of the overall system structure;(b)Physical picture
利用搭建的实验平台在晴朗的天气下进行户外实验测试,通过太阳跟踪系统对太阳进行了实时跟踪,其中太阳跟踪系统具有手动模式,可以手动控制位置,还具有自动搜索模式,可以俯仰方向扫描旋转±90°,水平方向扫描旋转±180°以找到太阳;之后完成了初步的太阳光谱观测,实测的太阳光谱数据如图16所示,其光谱波段为600~5000 cm−1的中红外区域,分辨率为0.5 cm−1。
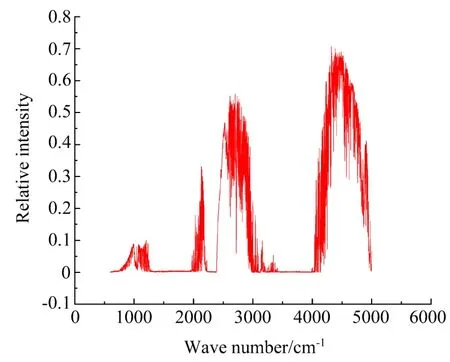
图16 实测太阳光谱Fig.16 Measured solar spectrum
5 结论
基于太阳掩星方法和傅里叶变换红外光谱技术,设计了一个用于太阳光谱地基跟踪遥感的光学系统。光路结构采用太阳跟踪系统、传输光路系统和FTIR光谱仪相匹配的型式。设计了一个能实现对太阳进行全方位跟踪且光通量稳定、结构简单的太阳跟踪系统,并建立光学模型,计算了跟踪太阳时太阳光斑移动轨迹的理论公式,为下一步实现在移动平台上进行高精度的太阳跟踪奠定了技术基础。设计了合适的传输光路系统,实现了太阳跟踪系统和FTIR光谱之间的光束耦合,进一步提高了光通量。利用Zemax对总体光路进行了优化设计,分析了FTIR光谱仪中抛物镜焦距对干涉条纹的影响,确定了满足系统需求的抛物镜焦距的大小,进一步对整个系统进行仿真。在满足系统的设计指标下,得出了四象限位置探测器的测量精度和系统跟踪精度的技术指标。并搭建实验平台进行了户外实验,测得的太阳光谱质量良好,验证了系统的合理性。

