三维矿山地质建模与空间分析探讨

陈 楠，谭 培

（1.四川省冶金设计研究院，四川 成都 610000；2.四川省冶勘设计集团有限公司，四川 成都 610000）

近些年来，社会科学技术获得突飞猛进的发展，计算机等硬件与软件设施得到进步，空间信息技术也得以综合应用，使得人们能够在短时间内及时获取大量的物理信息与几何信息，了解地球环境，为实现地球数字化发展，构建数字地球体系提供支持。矿山资源是社会经济发展的物质基础，矿山开采的规模和数量越来越大，如何综合性分析矿山地质环境与资源信息，以更加生动形象的方式将其展现出来，是现代矿山地质勘探以及空间分析的发展态势[1]。矿山区域的三维地质建模以及空间分析，均需要运用数据结构，综合三维可视化技术、图像处理技术以及计算机图形模拟，将矿产区域的空间数据形象、生动且有规律地表现出来，并且大量的分析与探究图形携带的信息。

1 三维矿山地质建模空间插值分析

构建三维矿山地质模型时所需要应用的数据信息主要是矿山开拓工程数据、钻孔数据以及勘测数据等，这些数据信息在大多数情况下是具有有限性的，并且分布存在着很多不规则的现象，但是矿山地质空间的数据信息具有多变性、复杂性和连续性。想要综合运用具有离散性和有限性的矿山地质信息得到地质形态的构造和恢复矿床形态，是构建矿山地质模型的重点和必要环节[2]。为确保信息数据的综合性运用，利用空间插值能够获得良好的效果，同时还可以将空间测量的数据信息进行快速转换，形成具有连续性的空间数据。空间插值的理论基础是对空间位置上的点做出假设，当这些点相互靠近的时候，便更加有可能获得相似的特征值，而当这些点相互之间的距离越远的时候，其表现出来的相似特征也就越小。

1.1 最近距离法

最近距离法又被称作梯森多边形法（Thiessen Polygons），这是一种分割研究空间的方法，所以又被叫作梯森分割（Thiessen Tessellaton）。这种方法可以简单地理解为内插空间的一种措施，任何一个未知的点所获得的数值在平面空间位置上均可以通过与其相临近点的数值予以替代

1.2 反距离加权法

空间内插方法中，反距离加权法也是最为常见的方法之一，这种方法在运用的时候认为未进行采样的点受到与其相临近点的贡献最大，总而言之，距离与贡献两个参数之间形成反比关系。反距离加权法的基本思想是把差值函数F（x，y）进行定义，加权平均处理各个数据点的函数值fk，其关系表达式如下所示：

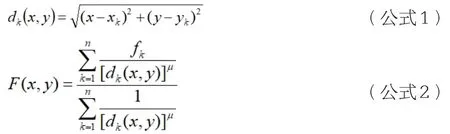
在公式1中，其所表示的含义为点(xk,yk)与点(x,y)两点之间的距离大小，μ的取值为2。

1.3 趋势面分析

分析趋势面的时候，主要是以空间抽样数据作为基础，利用拟合的措施获得数学曲面，通过数学曲面对空间内部的数据变化以及空间分布情况作出反映。分析趋势面的基本思路是首先利用已经获取的采样点数据拟合，得到陪你规划数学平面方程，其次在以数学平面方程组为基础，对没有测量值的点上的数据作出计算。趋势面分析具有较强的适应性，第一，可以立足于空间视点对残差与趋势进行诠释。第二，观测存在限制，内插也需要以有限的数据为基础。当残差和趋势可以与局部尺度和区域尺度进行联系的时候，趋势面分析则最具有意义。

1.4 多元回归

从数字形式层面上分析，多元回归类似于趋势面，但是却又同时存在着一定的不同。第一点，在趋势面分析中，A所表示的是坐标矩阵，但是在多元回归分析之中，A所表示的含义是任何变量值。第二点，在趋势面分析中，拟合地质模型需要严格遵守相应的拟合规则，基本上要按照常数、一次、二次、立方的顺序展开拟合，拟合过程中最为主要的是明确模型次数，所以趋势面分析存在着很多的内在多重共线性问题。在多元回归分析之中，即使也存在着多重共线性，但是多重共线性并非是内在的，在解决多重共线性时需要逐步回归，由此可见，就选择趋势面的次数而言，多元回归最为核心的问题是对模型作出区分以及合理化选择变量。

1.5 样条函数法

样条函数是通过函数逼近曲面的一种措施，样条函数在使用的时候具有很好的便利性，并且计算量相对较小，与空间统计法相比较而言，其特点集中在以下几个方面。第一，不需要预先估量与计算空间方差结构。第二，可以不用进行统计假设，若表面平滑，也可以保留精度。在平滑表面状态时，样条函数具有合理性，需要有连续性的一阶导数和二阶导数。样条函数适合于以很密的点实施内插等值线的情况。样条函数法在应用中同样存在着一定的不足，首先是不能够简单的估计出存在的误差，其次是具有较差的点稀时效果。样条函数具有较多的种类，在三维地质模型构建时应用最为普遍的是薄盘样条、张力样条以及B样条。

1.6 克里金差值法

在地质统计学之中，克里金插值法是一种常用的空间插值法。地质统计法的出现，为空间插值提供了一种全新的优化策略，具体而言就是在进行插值时基于某种优化准则函数，对变量数值动态化的做出决定。Krige以及Matheron等人在对插值法进行研究时，将重点集中在确定权重系数领域，进而保证内插函数始终保持最佳状态[3]。克里金插值法有协同克里金法、普通克里金法、指示克里金法、泛克里金法等等多种类型，克里金法的不同，所需要的条件也有所差异，在进行方法选择时可以根据实际的研究需求进行选择。当前空间插值法有很多，不同插值法所表现出来的优势和不足以及适用范围也各有不同。就大多数的空间插值法而言，没有绝对最优的方法，只有在特定条件下表现出其应用优势的方法，所以在构建矿山地质模型时，需要以实际情况为依据，综合探索空间环境获得数据信息，经过反复实验进行比较以选择合适的空间插值法。

2 三维空间分析

三维空间分析主要是基于数字高程模型，综合运用空间分析算法，以快速获取在某个区域范围之内的空间特征与区域之间存在的关系[4]。三维空间分析是GIS当中最为高级的分析功能，也是对GIS进行衡量的标准，通过三维空间分析，使用者可以快速的得到结果，并且分析空间特征信息，获得精准的结果。当前三维空间分析在应用之中所实现的功能主要有以下几点，第一，可以定位与查询任意点；第二，及时获取测量点的横向值、坡度值以及三维坐标值；第三，可以查询物体的体积、面积、距离以及坡度面积等等；第四，可以绘制剖面图。在三维空间分析之中，应用ArcObjects可以为使用者提供强大功能的三维分析组件，通过这些组件，使用者能够完成多种三维分析工作。

2.1 坡度分析

水平方向与局部地表之间形成的正切值被定义为坡度，坡度所包含的内容用斜度和坡向。斜度主要是指高度变化的最大值比率，坡度主要是指变化比率最大值的方向，分析矿产地区的地貌环境时，可以应用二阶差分凸率和凹率。

2.2 计算空间距离

计算空间距离时，应用的函数关系表达式如下所示：

在需要勘探的地质体上任意选取两点，通过上述公式获取两点之间的距离，需要注意的是，空间上的两点主要是指在相同的岩层上的两点。

2.3 计算多边形面积

在构架完成的三维地质模型中，计算多边形面积的思路是以二维环境为基础，综合积分原理中的梯形面积计算法。倘若是多边形为凹多边形，那么在进行计算的时候需要剖分多边形，使其成为多个凸变形进行面积叠加，亦或者是三角剖分凹多边形，之后再计算出三角形面积，完成叠加。其关系表达式如下所示：

2.4 绘制剖面图

地质勘探人员在了解地质结构时，最为常见的手段是绘制地质剖面图，为了能够尽可能多的从三维地质模型之中获取相应的剖面信息，进行切割时可以选择使用任意剖面进行模型分析。若是利用无限延展的平面对三棱柱体进行切割，那么将会得到多种切割方式。不考虑对称性，那么将会得到35种切割方法。若是考虑对称性以及相切情况，那么将会得到36种切割方法。

3 结束语

构建矿山三维地质模型以及进行空间分析是一项非常复杂的工程，近些年来，国内和国外的研究人员针对于三维地质模型构建以及空间分析展开了各种方式的研究。本文将以此为依据，系统性的概述当前三维矿山地质模型构建以及空间分析的方法，旨在为资源开采以及矿区地质环境监测提供借鉴。