针对SM4算法的功耗模板-碰撞分析

徐家俊，张翌维，赵 建，相韶华

深圳技术大学 大数据与互联网学院，广东 深圳518118

密码设备在运行密码算法时会泄露算法的执行时间、电磁辐射及能量消耗等若干物理信息[1]，侧信道攻击就是通过测量密码设备计算过程中的物理泄漏信息并进行统计分析的方法[1-2]，主要集中在功耗攻击、电磁攻击和时间攻击等。

Schramm等学者于2003年提出了内部碰撞的概念[3]，并对Feistel结构的DES算法进行了线性碰撞攻击。但该攻击方法处于研究早期，实际效果十分受限。随后，Bogdanov等学者于2007年提出了基于AES算法的线性碰撞攻击[4]。但是，直到2010年在CHES上，Moradi等学者对基于Pearson相关系数的AES掩码硬件实现了相关强化碰撞攻击后[5]，才使得碰撞攻击具有实践可能。之后，王安等国内学者于2015年对掩码AES智能卡实现了高效的碰撞攻击[6]，而Bruneau等国外学者在碰撞攻击基础上，于2017年提出了一种新的随机碰撞攻击方法（Stochastic Collision Attack）[7]，逐步改进了碰撞攻击。上述攻击的演进及目前侧信道碰撞分析[8-10]都主要聚焦在AES算法类SPN密码结构，对于Feistel结构碰撞分析的相关研究文献仍比较少。

基于非平衡Feistel结构的SM4密码算法，作为国内官方公开的第一个商用密码算法[11]具有重要地位，对其进行侧信道分析有利于提高SM4算法的综合安全能力。目前，国内外针对SM4算法的侧信道分析主要集中在侧信道功耗攻击及其掩码防护等方面[12-18]，但仍未出现利用内部碰撞的原理，对SM4算法进行侧信道碰撞分析的文献。

本文结合内部碰撞原理，在分析SM4算法非平衡Feistel结构后，结合内部碰撞原理，将算法加密过程中的中间变量值（如S盒输出）作为分析目标，利用每一轮各S盒输出值碰撞来恢复轮子密钥，通过功耗模板-碰撞分析方法成功恢复出了SM4算法前四轮的子密钥，从而反推出SM4算法的初始密钥。

1 SM4算法及碰撞攻击原理简介

1.1 SM4算法加密过程

SM4密码算法是一种32轮的迭代非平衡Feistel结构分组加密算法[11]。该算法的分组长度为128 bit，密钥长度为128 bit。加密算法与密钥扩展算法都采用32轮非线性迭代结构。解密算法与加密算法的结构相同，只是轮密钥的使用顺序相反，解密轮密钥是加密轮密钥的逆序。SM4算法加密流程结构如图1（a）所示。

从图1（a）可以看出，SM4加密算法输入128 bit明文后，被分割成PL和PR左右两部分，分别为32 bit和96 bit，右半部分PR与子密钥rki（i=0，1，…，31）进行异或操作，经过合成置换T后，再与左半部分PL进行异或操作，得到下一轮32 bit的中间数据Xi+4（i=0，1，…，31）。经过32轮重复操作后，会在最后一个轮次中得到中间数据X35，并且会将X32||X33||X34||X35合并成一组128 bit的中间数据。最后，合并的中间数据会经过反序变换R得到128 bit的密文。

图1（b）为SM4算法合成置换T，其中包括非线性变换τ和线性变换L两个操作。每一轮长度为96 bit的右半部分PR被分割成3个32 bit字，然后与当前轮子密钥rki（i=0，1，…，31）异或，即Xi+1⊕Xi+2⊕Xi+3⊕rki，输出值即为合成置换T输入的32 bit。其中，非线性变换τ是一个8 bit进8 bit出的S盒替换操作；线性变换L是一个循环左移操作，即L(B)=B⊕(B<<<2)⊕(B<<<10)⊕(B<<<18)⊕(B<<<24)，其中B为经过非线性变换τ后的输出值。

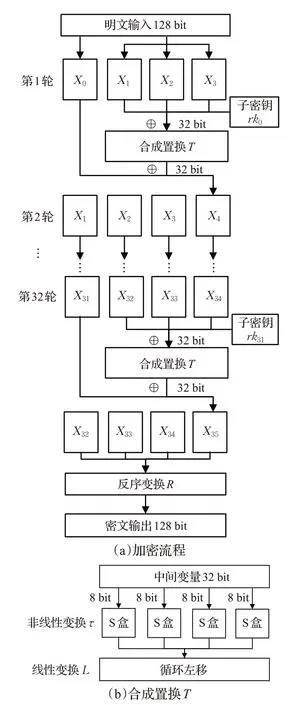
图1 SM4加密算法流程

密钥扩展算法结构与加密算法结构基本相同。若加密密钥MK=(MK0,MK1,MK2,MK3)，其中(i＝0,1,2,3)。令密钥(i＝0,1,…,35)，轮密钥为rki∈(i＝0,1,…,31)，则轮密钥生成方法如下：

（1）令(K0,K1,K2,K3)=(MK0⊕FK0,MK1⊕FK1,MK2⊕FK2,MK3⊕FK3)，其中FKi(i＝0,1,2,3)为系统参数。

（2）轮密钥rki=Ki+4=Ki⊕T′(Ki+1⊕Ki+2⊕Ki+3⊕CKi)，其中CKi为固定参数，合成置换T′与加密算法轮函数中的T变换基本相同，只将其中的线性变换L修改为L′变换，即L′(B)=B⊕(B<<<13)⊕(B<<<23)。

1.2 碰撞攻击原理

Schramm学者等人于2003年在FSE上提出了“内部”碰撞攻击的概念[3]。如果在一个密码算法中某个函数输入两个不同值，对应该函数的输出若相同，则称发生了内部碰撞。碰撞攻击的基本思想是寻找特定位置的碰撞，通过碰撞产生的关系推导出密钥信息，即每发生一次碰撞都会减小密钥搜索空间。因此，只要碰撞发生达到一定次数后，便可通过碰撞产生的关系式恢复出原始密钥。

图2为碰撞攻击原理示意图。首先，若选择攻击目标为算法加密过程中的S盒输出值Y1、Y2，并记密钥之间的差值为Δk，即Δk=K1⊕K2。若要使得算法加密过程中的S盒输出值发生碰撞，则在S盒输入前明文P1、P2需满足等式P1⊕K1=P2⊕K2，便可以通过上述等式反推出Δk=P1⊕P2，即P2=P1⊕Δk。因此，通过输入特定的明文，使得P1和P2之间的关系满足等式P2=P1⊕Δk，并提取所有明文加密过程中第一个S盒的功耗曲线，即加密位置S1作为第一条功耗曲线，第二个S盒加密位置对应点S2作为第二条功耗曲线，那么此时两条功耗曲线的相似程度应该比较高。

图2 碰撞分析原理示意

通过遍历差值Δk从0至255的所有可能，可以使得明文P1和P2之间的关系满足等式P2=P1⊕Δk。若构造256条明文，令其P1依次遍历0至255，P2与P1相同，也依次遍历0至255。那么对于第i（i=0，1，…，255）个明文的P1来说，满足P1=i并且P2=P1⊕Δk的就是第i⊕Δk个明文了。反映在波形上，也就是Ti片段中S1的功耗曲线与Ti⊕Δk片段中S2的功耗曲线相似度较高。由此，通过波形反推，便可得到密钥之间的关系。

2 针对SM4算法的功耗模板-碰撞分析

针对SM4算法的功耗模板-碰撞分析方法，本文方法通过使用了内部碰撞原理，并结合汉明重量模板匹配方式来恢复SM4算法原始密钥。

根据1.2节可知，基于内部碰撞原理的侧信道攻击方法，可以在不需要知道中间值，也不需要知道中间值泄露模型，只需要确定并知道两个中间值相等的情况下，即可通过建立等式方程来获得密钥信息。因此，一方面，相比于主流的侧信道分析方法，如相关功耗攻击（CPA）和差分功耗攻击（DPA），本文方法可以在不需要假定中间值泄露模型的情况下通过建立等式方程来获得密钥信息；另一方面，由1.1节SM4算法结构可知，本文目标SM4算法在加密及子密钥处理方面较为混淆及扩散，密钥恢复具有一定难度，而本文方法能在基于内部碰撞原理的基础上，结合模板匹配方法，可以进一步降低密钥搜索区间。

因此，综合分析SM4算法后可知，针对SM4算法的功耗模板-碰撞分析方法，可以在不需要建立中间值泄露模型的情况下，通过模板匹配进一步降低密钥搜索区间，并成功恢复SM4算法全部子密钥。

针对SM4算法结构可知，该算法的初始密钥至少需要经过4轮加密，才能达到完全的扩散及混淆。因此，基于SM4算法的侧信道分析，只需要针对其前4轮加解密运算即可。针对SM4算法S盒输出值进行的功耗模板-碰撞分析，前4轮分析过程如图3所示。

图3 分析过程

（1）有选择地输入N组明文Pi(p1,p2,…,pN)进行加密操作，同时分别采集并记录每一轮各S盒的输出功耗曲线T(i,m)(t(1,m),t(2,m),…,t(N,m))，其中m(m=1,2,3,4)表示当前轮次的第m个S盒。

（2）构造每一轮各S盒输出值Rm碰撞，并通过模板匹配筛选候选子密钥。

（3）通过构造碰撞阶段中的方法反推出每轮子密钥值rki(i=0,1,…,15)。

（4）获得算法4轮子密钥，通过密钥扩展算法反推出原始工作密钥K。

其中，SM4算法32轮加密过程中的整体功耗曲线如图4所示。

图4 SM4算法32轮加密过程的功耗曲线

2.1 构造第一轮碰撞

本文方法的分析过程主要分为构造碰撞和模板匹配两个阶段。构造碰撞阶段首先需要针对SM4算法第一轮加密过程，并在此基础上对算法的第二、三、四轮加密过程进行分析。

图5 第一轮流程

（1）令输入明文的后96 bit的任一字节Xi(i=4,5,…,15)为基准字节，如选择X12为基准字节，则可以令X12为（00）16，同时对X13、X14、X15（即图5中明文输入的A、B、C）进行遍历（00～FF）16。在遍历过程中，当X13、X14、X15中的某一个字节与X12产生碰撞后，则对应字节所获取到的S盒输出功耗曲线应该大致相同，记录当下对应字节所输入的明文v1，并对剩余字节进行后续遍历。重复上述操作，直至获得该轮选择输入的明文字节vi(i=0,1,2,3)后，则分别获得本轮S盒输出字节res0 es1、res0 es2、res0 es3的碰撞。

（2）根据算法加密流程可知，在第一轮加密过程中，若中间变量S盒输出发生碰撞，以X12与X13为例，则有以下等式S(X12⊕rk(0,0))=S(X13⊕rk(0,1))=resi，其中resi(i=0,1,2,3)为S盒输出值。对于同一个密码设备（黑盒），密钥值虽然未知但是固定。因此，可把rk(0,0)和rk(0,1)理解为一个固定值，即它们的差值∆K1也是固定值，则可以推出等式rk(0,0)⊕rk(0,1)=X12⊕X13=∆K1。由上述例子可知，每一轮的子密钥差值∆Ki(i=0,1,2,3)为固定值。因此对于上述遍历得到的选择输入的明文字节v1、v2、v3，以明文输入字节X12为基准的情况下，可分别得到子密钥差值∆K1、∆K2、∆K3，即：

本文方法在分析中选取加密过程的中间变量S盒输出值作为分析目标，这是因为在具体实现工程中S盒输出的功耗往往更为显著，需说明的是，理论上也可采用中间变量S盒输入值作为分析目标。

与传统的线性碰撞分析相比，本阶段通过子密钥差值∆Ki(i=0,1,2,3)可有效快速构造SM4算法第一轮S盒输出值内部碰撞。令输入明文的前12个字节为（00）16，使用后4个字节来构造S盒输出值碰撞。构造第一轮S盒输出值碰撞流程如图5所示。

以此，第一轮子密钥恢复公式如下：

经过构造第一轮各S盒输出值碰撞后，采集到的第一轮各S盒输出的功耗曲线如图6所示。其中，明显看出第一轮各S盒的输出功耗曲线大致相同。

图6 第一轮发生碰撞各S盒的功耗曲线

2.2 构造第二、三、四轮碰撞

在构造第一轮各S盒输出值碰撞后，获得候选子密钥，并用于下一轮的分析。以算法第二轮分析为例，分析方法如下。

首先，建立输入明文与中间变量Xi的数学关系。通过构造算法第一轮S盒输出碰撞后，可以获得第一轮的候选子密钥，以此用于下一轮的分析。通过文献[19-20]可知，SM4算法前后轮次的中间变量可以通过以下数学关系计算。

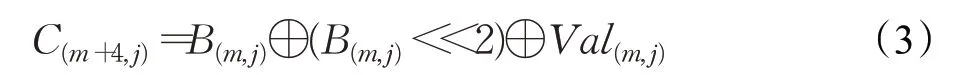
其中，m表示轮次(m=0,1,2,3)，j表示该轮的第j个字节（j=0,1,2,3），B(m,j)表示第m轮第j个字节经过S盒变换输出后的值，<<为算术左移操作。在上述公式中，Val(m,j)为固定值，根据文献[20-21]可知，其计算等式如下：

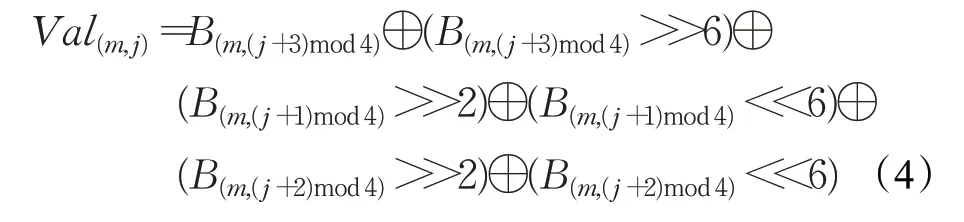
该计算公式是基于算法第一轮各S盒发生碰撞，并根据第一轮子密钥恢复公式获得候选子密钥后，对输入的128 bit明文进行逐列构造，使得下一轮的各S盒输出值发生碰撞。例如，对于SM4算法第二轮S盒输出的各个字节，可以按以下方式构造。

第二轮S盒输出的第一字节所对应构造的明文：

第二个字节：

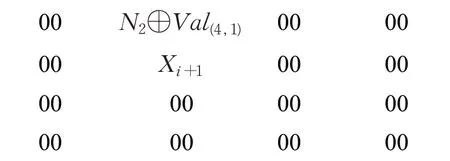
第三个字节：

第四个字节：

其中Ni(i=1,2,3,4)为变量，需要遍历256次（00～FF）16，Xi为第一轮候选子密钥的每一个字节与（71）16异或后的值。通过SM4算法逆S盒替换表可知S(71)输出值为（00）16，因此通过异或（00）16可以简化算法中间变换操作。以此方式对第二轮S盒输出的每一个字节进行选择明文输入，通过遍历可使得第二轮各S盒输出值发生碰撞（如第一轮），即可获得第二轮的候选子密钥。其中，第二轮子密钥恢复公式如下：

以SM4算法第二轮为例，经过选择明文对本轮各S盒输出值构造碰撞后，采集到的第二轮各S盒输出值发生碰撞的功耗曲线如图7所示。其中，图中选中的部分为使用本轮方法构造后，各S盒输出值发生碰撞的功耗曲线，可明显看出第二轮各S盒的输出功耗曲线大致相同。调整相应的Val值和子密钥恢复公式，可对算法第三、四轮重复上述方法。

图7 第二轮发生碰撞各S盒的功耗曲线

2.3 汉明重量模板匹配

通过对算法前4轮进行构造上述碰撞方法后，根据每一轮的子密钥恢复公式，可以获得每一轮的候选子密钥。因此，通过汉明重量模板曲线匹配每一轮各S盒输出发生碰撞的功耗曲线，可以筛选候选子密钥，进一步降低密钥搜索区间。

其中，汉明重量通常是指一串符号中非零符号的个数。在密码算法中，一个字节的汉明重量大小为该字节中比特1的个数。因此，从字节（00）16到（FF）16，该256个字节可以划分为9种大小不同的汉明重量，每种汉明重量的统计数量由表1所示。

表1 0x00～0xFF中每种汉明重量所对应的统计数量

功耗曲线可以由多元正态分布(m,C)模板刻画[1]，其中多元正态分布由协方差矩阵C和均值向量m构成。因此，在汉明重量模板匹配过程中，实际测量的功耗曲线t和(m,C)汉明重量模板可以通过极大似然准则来评估，判定该实际功耗曲线与汉明重量模板相匹配的概率大小。通过计算匹配概率值大小可以反映出该汉明重量模板与实际功耗曲线的匹配程度。其中，评估准则公式如下：

该概率公式中的(t-m)′为实际功耗曲线ti(i=0,1,…,n)与均值向量m之差的转置矩阵，C-1为协方差矩阵C的逆矩阵，det(C)为协方差矩阵C的行列式，n为特征点数量。其中，特征点是汉明重量功耗模板曲线中具有显著区别的点。图8为9种汉明重量功耗模板曲线。其中，部分所选取的特征点与其正态分布如图9所示。

图8 汉明重量功耗模板曲线

图9 特征点的正态分布

从图9中可明显看出，所选取的特征点符合正态分布特征，各特征点值均处于正态分布的中间位置，则表明所选特征点发生频率较高，在汉明重量功耗模板曲线的特征表征中较为稳定。

通过计算汉明重量功耗模板曲线与实际功耗曲线的匹配概率程度，取其中匹配概率最大值所对应的模板曲线的汉明重量值，并根据每一轮各子密钥恢复公式，筛选候选子密钥。然后通过遍历候选子密钥进行验证，即可恢复出每一轮的子密钥。

上述分析方法可以成功恢复出SM4算法前4轮子密钥rki(i=0,1,…,15)，并通过SM4密钥扩展算法反推，可以成功恢复出SM4算法的初始密钥K。

3 结果验证及实验分析

3.1 结果验证

本功耗模板-碰撞分析的目标是基于STM32F407（ARM Cortex-M4）嵌入式测试板上搭载的SM4算法，功耗曲线是在Inspector平台下进行采集，使用的分析工具包括Current-Probe及WaveRunner-8104示波器。实验验证了该方法的有效性。

通过功耗模板-碰撞分析，根据式（1）、（2）能成功恢复出第一轮子密钥为“0x34D43155”，如表2所示；通过式（3）、（4）、（5）能成功恢复出SM4算法第二轮子密钥为“0x9CC0AD30”，如表3所示。重复上述方法，可以获得SM4算法第三、四轮子密钥分别为“0x9608FEEF”“0x830DD75D”，成功恢复SM4算法前4轮全部子密钥rki(i=0,1,…,15)，其中第三、四轮子密钥分析结果如表4、5所示。最后，通过SM4密钥扩展算法进行反推，可以成功恢复出算法原始密钥为“0x52697363757 2654368696E6132303137”。

表3 第二轮分析结果

表4 第三轮分析结果

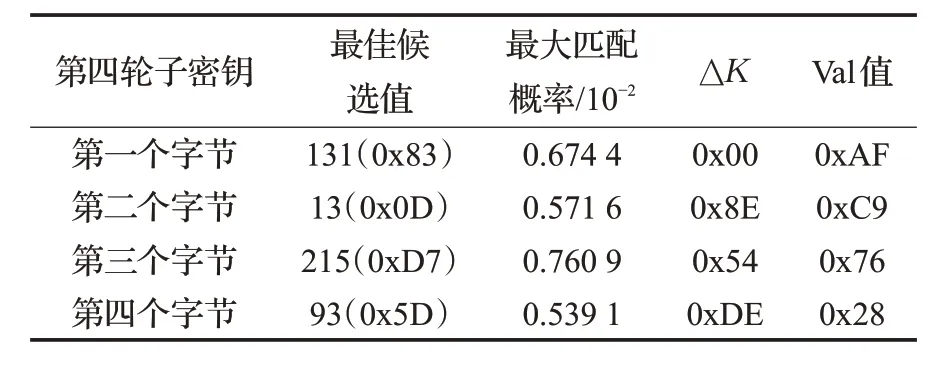
表5 第四轮分析结果

3.2 实验分析

传统线性碰撞攻击是通过固定明文和第一个S盒对应字节的子密钥，遍历猜测子密钥k2为0～255，总会得到一个子密钥k2，使得明文p1与密钥k1满足等式p1⊕k1=p2⊕k2。同理，可以得到子密钥k1与k2～k16之间的对应关系，从而降低密钥的猜测空间。反映在波形上，则是只能得到汉明重量等式HW(p1⊕k1)=HW(p2⊕k2)，无法得到k1和k2的确切对应关系。如果采用线性碰撞攻击的方法，得到上述汉明重量等式后，遍历猜测k2及后续密钥的所有可能，效率较为低下。针对SM4算法，若使用传统线性碰撞攻击方法，则对于第一轮子密钥的恢复，需要对任意两个密钥字节进行遍历搜索，所以时间复杂度为O(264)，数据搜索空间为[0，26−1]，对于第二、三、四轮的子密钥恢复，则需要搜索整个数据区间，所以时间复杂度为O(2128)，数据遍历搜索区间为[0，2128−1]。

主流的侧信道分析方法，如相关功耗攻击（CPA）和差分功耗攻击（DPA），都需要在采集实际功耗曲线后，对目标算法进行中间值泄露模型建模。而根据1.2节可知，基于内部碰撞原理的侧信道攻击方法，可以在不需要知道中间值，也不需要知道中间值泄露模型，只需要确定并知道两个中间值相等的情况下，即可通过建立等式方程来获得密钥信息或直接求解密钥。因此，针对SM4算法的功耗模板-碰撞分析方法，可以在不需要假定中间值泄露模型的情况下，通过构造碰撞方法采集特定的功耗曲线，以确定算法加密过程中中间值相等，即可通过建立的等式方程来获得密钥信息，并通过模板匹配进一步降低了密钥搜索区间。

结合内部碰撞原理侧信道分析的优势，根据针对SM4算法的功耗模板-碰撞分析方法可知，本文方法对SM4算法四轮的运算过程中包含的循环运算次数上限为256次，即28，每轮独立遍历次数最多为4次，所以该算法的时间复杂度上限为28×24=212，即O(212)，搜索数据区间为[0，28−1]。

两种碰撞攻击方法的性能对比如表6所示。根据上述两种碰撞攻击方法的性能对比后可知，虽然本文提出的功耗模板-碰撞分析方法需要额外制作模板曲线，但是从算法性能上对比两者方法可知，本文给出的功耗模板-碰撞分析方法均要优于传统线性碰撞攻击。综上，本文方法不仅降低了计算复杂度，并将碰撞攻击扩展到非平衡Feistel算法结构，提高并增强了碰撞攻击的适用性与实用性。

表6 两种碰撞分析方法性能比较结果

4 结束语

本文针对非平衡Feistel结构SM4算法给出了一种功耗模板-碰撞分析方法，利用构造特殊明文的方式，以每一轮各S盒输出值碰撞来恢复轮子密钥，并在STM32F407测试板上分析了SM4算法，成功验证了该分析方法的有效性。此外，在每一轮中采用了汉明重量模板匹配来筛选候选子密钥，进一步降低了密钥搜索区间。相比于传统侧信道碰撞攻击方法，本文方法不仅提高了碰撞攻击的分析效率，而且增大了碰撞攻击在非平衡Feistel结构实现上的适用性。进一步的，拟对不同分组密码结构进行碰撞分析模型的理论抽象，实现统一分析模型，扩展碰撞攻击在不同密码工程中的应用。