基于高斯拟合的光纤法珀相关解调算法研究

左方俊，贾平岗，韩 超，冯 飞，熊继军

(中北大学 电子测试技术重点实验室，山西 太原 030051)

0 引 言

光纤法珀传感器的主要原理是将被测物理量转化为光纤法珀传感器的腔长，通过腔长的变化反映出相应物理量的变化，由于光纤法珀传感器具有良好的抗腐蚀和抗干扰特性，目前已被广泛应用于桥梁健康监测[1]、 核电健康监测[2]、 发动机脉动压力检测等领域. 光纤法珀传感器信号解调的方法主要有强度解调[3]和相位解调[4]，强度解调的解调速度快，但是解调范围有限，而相位解调法的解调精度高、 解调范围大，目前，常见的相位解调法包括峰值追踪法[5]、 傅里叶变换法[6]以及相关运算解调法[7], 在相关运算解调法中非扫描式互相关解调系统因为使用硬件进行互相关运算，拥有可动部件少、 成本低、 准确性高等优点而受到了广泛的研究.

非扫描式相关光纤法珀解调的解算方法主要包括： 基于干涉图样相位的解调法和基于干涉图样位置的解调法等. 2015年，李钧寿等人[8]利用小波提取干涉图样的包络，采用包络最大值位置解调光纤法珀传感器的腔长，腔长解调的误差仅为5 nm； 2020年，Wang等人[9]利用质心法解调峰值位置，再利用7步相移法解调出干涉图样的相位信息，从而解调出峰位的准确位置，配合相应的传感器，满量程的测量误差低于0.019%. 目前的算法无法同时满足解调精度和解调速度的要求，因此提高算法的解调精度和速度对光纤法珀传感器的应用具有重要意义. 本文根据非扫描式光纤法珀解调的原理，分析了非扫描式光纤法珀解调系统的信号特点，研究了一种基于高斯拟合的解调算法； 通过软件仿真分析了该算法的可行性和可靠性，并在FPGA+DSP的样机系统上对该算法进行了实验验证.

1 非扫描式相关解调原理

非扫描式光纤法珀传感器的解调系统由宽带光源、 1×2耦合器以及解调仪组成，该解调系统使用宽带光源供光，宽带光源发出的光耦合进62.5/125 μm 的光纤后，沿着1×2耦合器传输至光纤法珀传感器，在法珀腔的内部发生多光束干涉，法珀传感器的反射光携带腔长信息返回至耦合器，经过耦合器的分光，其中一路反射光从耦合器的另一端出射，最后经过准直系统的变换后在光楔表面发生干涉，干涉的透射光由光电耦合器件(CCD)探测，实现光电转换，转换后的模拟电信号经过硬件电路的采集处理后就能解算出传感器的腔长信息，系统的原理如图1 所示.

图1 解调系统示意图Fig.1 Diagram of demodulation system

根据非扫描式相关解调的原理[10]，CCD探测到的光强在空间上的分布满足

式中：I(λ)为光源随波长的分布函数；R1为传感器两个端面的反射率；R2为光楔两个面的反射率；L为法珀传感器的腔长；l为光楔两个面之间的厚度；λmax和λmin是光源的波长范围；I(λ)为光源的光谱分布.

根据相关解调的理论，当L=l时会出现干涉峰的最大值，而光楔两个面之间的厚度l的大小与CCD的像元位置是一一对应的，即在L=l处CCD探测到的光强达到最大，通过解算CCD像元探测到的光强最大位置就能解调出腔长.

由于CCD的像元是离散的，每个像元之间有一定的间隔，而式(1)所示的光强分布是连续的，光强最大值出现的位置有可能在两个像元的中间，这就降低了解调的精度，此时需要算法拟合两个像元间隔处的光强分布，从而提高解调的精度. 为此本文对式(1)进行理论仿真，取法珀传感器的腔长L=15 μm，即可得到如图2 的光强随光楔厚度l的分布，通过观测发现，干涉信号的每个峰都呈现一种类似于高斯分布的状态，可以采用高斯拟合的方法得到连续的光强分布，对图2 所示的信号进行测试，取光强最大位置附近的N个数据进行高斯拟合，得到如图3 的拟合曲线，经过数学理论计算，曲线的拟合度可以达到0.999 92，拟合曲线与非扫描式光纤解调仪的干涉图谱有比较高的拟合度，因此，光强最大位置附近的信号可以用高斯拟合来确定光强出现最大位置处的详细坐标.

图2 干涉信号仿真Fig.2 Simulation of interference signals

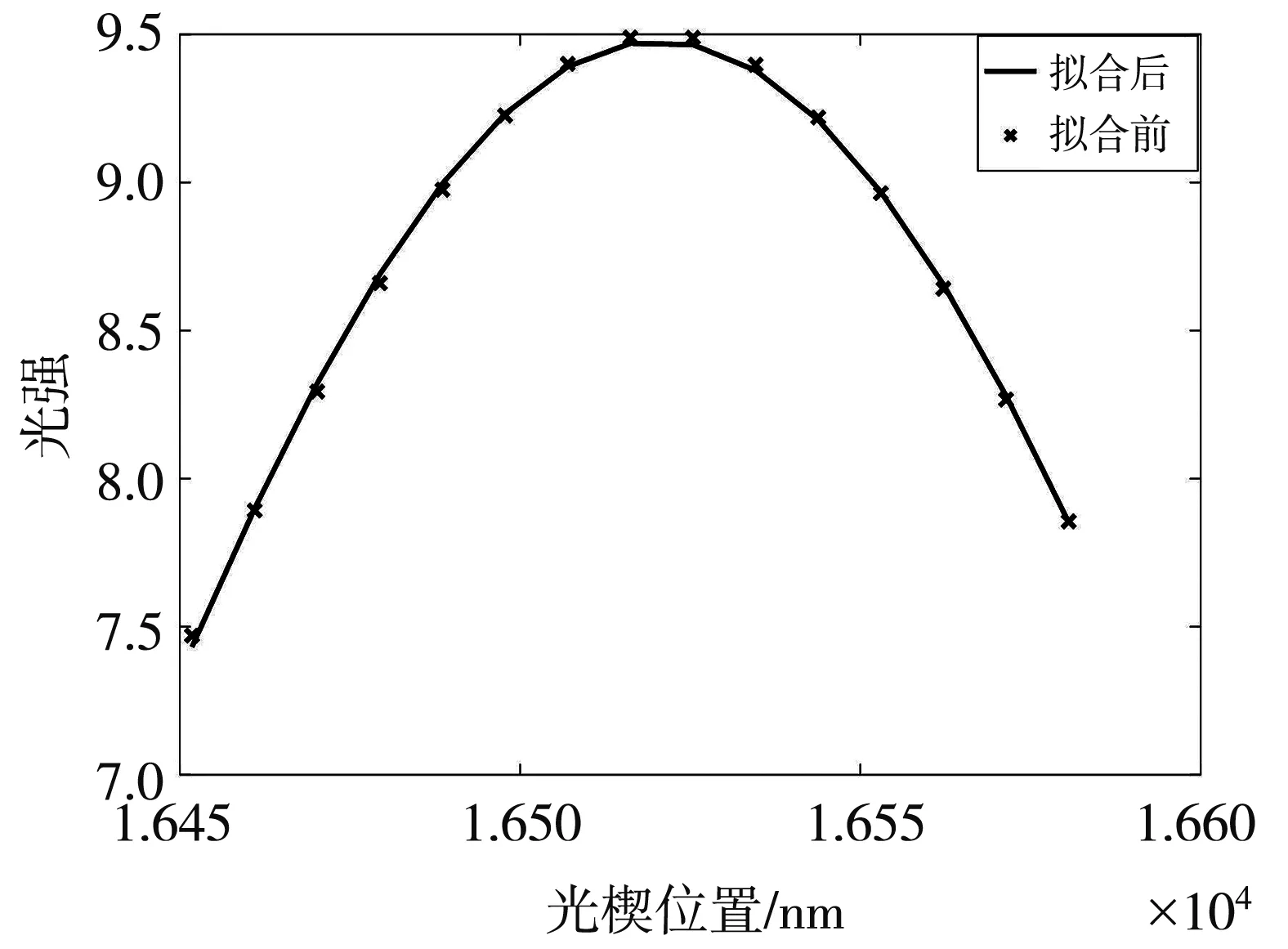
图3 峰值附近的信号Fig.3 Signals near the peak

2 高斯拟合算法

由于非扫描式互相关解调系统的干涉信号在峰值处与高斯函数具有非常高的拟合度，因此本文研究了一种基于高斯拟合的非扫描式互相关解调系统的算法，该算法以非扫描式光纤法珀解调原理为基础，先通过最大值寻峰算法寻找到相关信号的位置，再采用高斯拟合求出精确的位置，提高解调精度.

2.1 高斯拟合原理

高斯函数[11]的一维形式为

y=Aexp(-(x-u)2/2σ2.

(2)

对式(2)两端同时取对数，得到化简形式

(3)

令

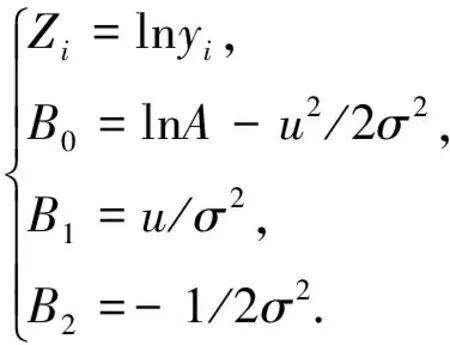
(4)

将所有试验的数据带入式(3)，即可得到如式(5) 所示的矩阵

(5)

简记为

Z=XB.

(6)

根据最小二乘原理得到

B=(XTX)-1XTZ.

(7)

根据式(4)即可得到高斯函数峰值位置以及峰值.

2.2 算法仿真

算法采用最大值寻峰算法与高斯拟合算法相结合的方式，实现光纤法珀传感器的腔长解调，具体实现流程如下：

1) 利用最大值寻峰算法找到CCD采集到的最大信号的粗略像元位置Pn；

2) 提取出最大信号的像元左右各12个点的信号强度In-12，In-11,…In+11,In+12；

3) 将取出的信号强度In以及对应位置Pn进行高斯拟合，得到高斯拟合函数的峰值和峰值位置(Im,Pm);

4) 对得到的Im进行标定，即可得到传感器腔长L.

为了确定算法的可行性与稳定性，采用软件对CCD的采样过程进行模拟，并用高斯拟合算法和最大值寻峰算法对数据进行解调. CCD探测到的光强分布服从式(1)，仿真过程中取传感器两个端面的反射率R1=0.04，光楔两个面的反射率R2=0.3； 传感器腔长为16 520 nm，得到10 240个点理想的光强分布，为了模拟CCD的采样过程，将数据每隔5个点采样1次，得到了CCD采集到的光强随像元分布的图样.

分别使用最大值寻峰法、 高斯拟合法对图4 所示的CCD采集信号进行解调仿真，为了模拟实际的信号质量，仿真过程中在信号中加入高斯白噪声，使得信号信噪比为30 dB. 传感器的初始腔长设定为16 520 nm，每次仿真腔长的增加量为1 nm，连续仿真1 000次，腔长总变化量1 μm，仿真结果如图5 所示，从图5 中可见，由于采集数据的离散化，最大值寻峰算法解调出来的腔长呈现一种阶梯状的变化，而高斯拟合后的解调结果呈现一种良好的线性变化. 这与仿真的设定相吻合，将仿真的1 000组解调结果与理论腔长之间作比较，得出仿真的理论误差如图6 所示，在1 000次的仿真过程中，使用高斯拟合算法的最大误差为2.18 nm，误差平均值为0.998 6 nm，计算误差在±2 nm之间，具有良好的解调精度. 在仅仅使用最大值寻峰法的情况下，解调结果如图7 所示，在1 000次的解调结果中解调误差最大可达7.674 nm，整体误差比较大，因此，高斯拟合算法对于最大值寻峰算法的解调精度有极大的提高.

图4 CCD采集仿真

图5 仿真1 000次的解调结果Fig.5 Simulate the demodulation results of 1 000 times

图6 高斯拟合解调误差

图7 最大值寻峰法解调误差

为了验证算法的稳定性，在信号信噪比为30 dB 的情况下，设定传感器腔长为16 520 nm，在保持传感器腔长不变的情况下，对信号进行1 000次的连续解调仿真，解调结果如图8 所示，在这1 000次的解调仿真过程中，解调结果的最大误差为1.93 nm，连续测量的1 000组数据的标准差为0.288 6 nm，解调结果的波动比较稳定.

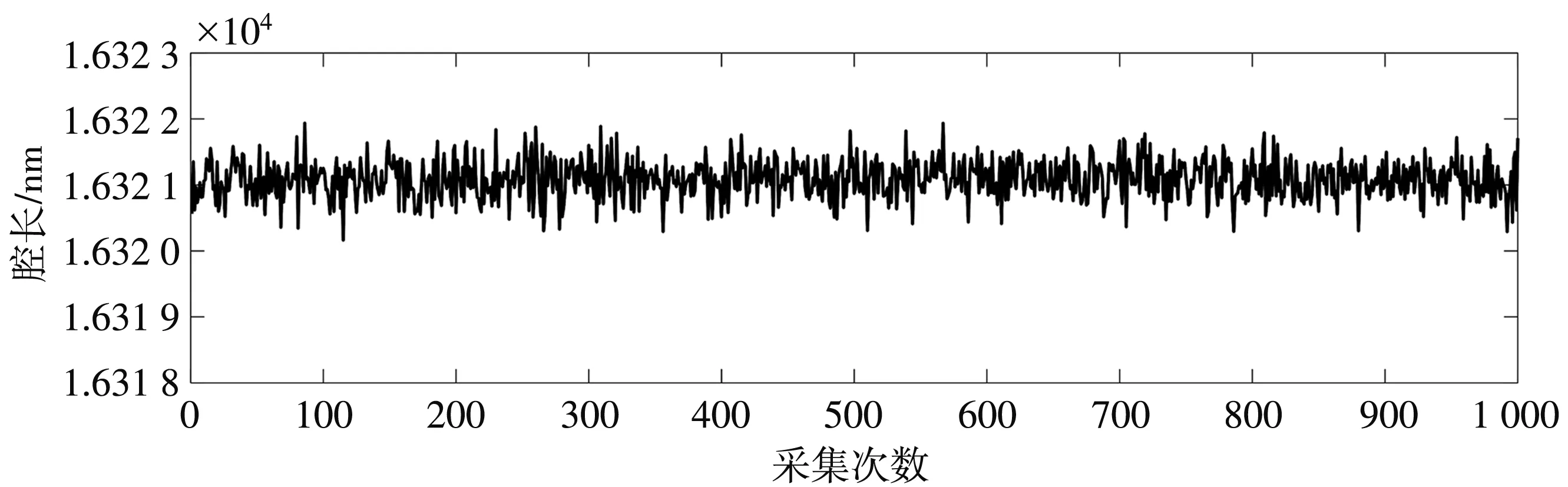
图8 腔长不变时的1 000次解调结果

为了仿真高斯拟合算法在不同信噪比情况下的解调结果的变化，使用软件对高斯拟合算法进行仿真，传感器腔长为16 520 nm，得到图2 的理想信号，在仿真的信号中加入不同能量的高斯白噪声，使得信号的信噪比分别为20 dB，30 dB，40 dB，50 dB 以及60 dB，再使用寻峰与高斯拟合结合的算法对信号进行解算，结算结果如表 1 所示.

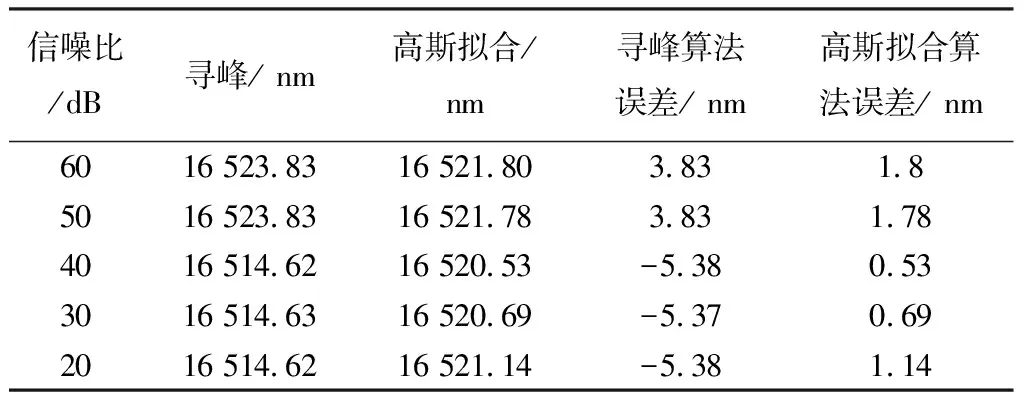
表 1 不同信噪比情况下的解调结果Tab.1 The result of demodulation under different SNR

当信号的信噪比较高时，最大值寻峰算法的解调结果比较稳定，解调结果与理论值之间的差值为3.83 nm，加入高斯拟合的解调结果与理论值最大相差1.78 nm，加入高斯拟合算法的解调结果更为精确. 在信号信噪比较低时，最大值寻峰算法的解调结果与理论值相差5.4 nm，而加入高斯拟合算法后的解调误差最大为1.14 nm，因此加入的高斯拟合算法具有良好的抗干扰特性，解调的信号不需要具有较高的信噪比，但是由于高斯解调算法的应用前提是寻峰算法解算出峰值最大值的大概位置，信噪比太低会影响寻峰算法的解调结果. 加入的高斯拟合算法具有抗干扰的能力，在一定程度上降低了滤波器设计的难度.

3 实验测试

为了检验在实际工况情况下算法的性能，设计了一台处理器为FPGA+DSP的解调样机，样机使用TCD1304对信号进行采集，该款CCD拥有2 048个像元，探测灵敏度可达160 V/(lx·s)，采集出来的信号先在FPGA中实现最大值寻峰算法，对原始谱进行初步解调求出峰位，然后将相关数据传输至DSP中，实现高斯拟合以及数据标定，解调样机采集到的原始谱如图9 所示，经过多次测量，该算法在DSP中运行的时间大概为 700 μs.

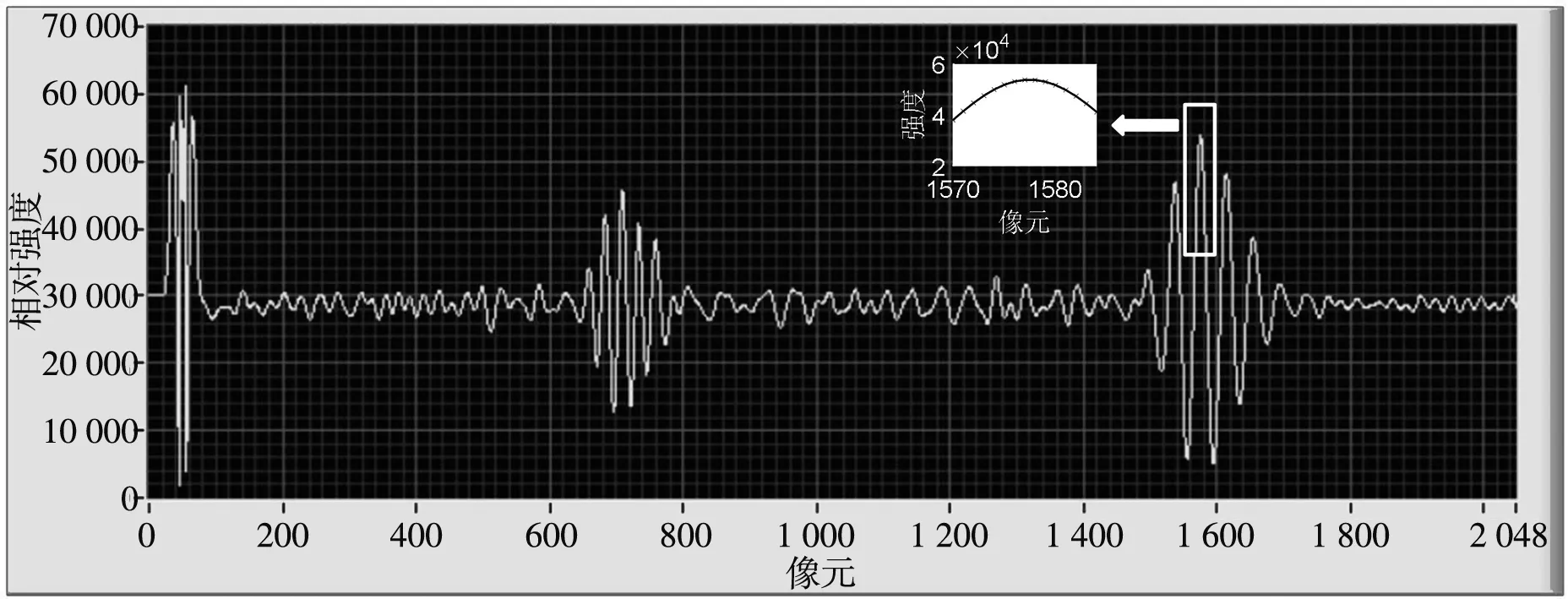
图9 CCD采集的光强分布Fig.9 Light intensity distribution collected by CCD

为了测量系统的稳定性，系统对光纤法珀传感器进行解调，连续测量800次，采集到的解调结果如图10 所示，采集的数据平均值为 16 420.25 nm，解调结果误差的均方值为1.643 nm.

图10 系统稳定性测试Fig.10 The stability test of system

4 结 论

本文研究了一种基于高斯拟合的非扫描式相关解调算法，利用非扫描式相关解调原理中CCD采集光强的分布形式，对峰位进行高斯拟合，从而获得高精度的峰位解调，仿真证明，该算法有比较好的抗干扰性能，可以抑制信号噪声对解调的影响，解调的精度比较高，实际检验证明，该算法的解调精度可以达到1.643 nm，在FPGA+DSP的硬件电路上解调的运算时间只有700 μs，硬件的解调时间短，对于非扫描式相关解调的工程化具有较大的应用价值.