基于自适应小波神经网络在压制地震勘探低频噪声中的应用

李光辉，张子豪，李佳蓉

(山西大学 物理电子工程学院，山西 太原 030016)

地震勘探是油气勘探的主要方法之一，高质量地震勘探记录是后续地质解释工作的基础. 对于地震勘探资料提出的“三高”(高信噪比，高保幅度，高分辨率)要求中，高信噪比是最基础最重要的要求. 随机噪声作为影响地震记录的主要因素，具有无规则、 非线性、 非平稳、 非高斯等特性，如何在压制随机噪声的同时保留有效信号是地震信号处理的难点之一，也是提高地震资料记录质量的主要环节. 沙漠地区油气资源极其丰富，但沙漠地区高频信号和噪声被松散的地表覆盖层吸收，因此，沙漠记录中的随机噪声和信号能量主要集中在低频区域，噪声能量大，且与信号在幅值和频谱方面都严重混叠，给勘探工作带来了极大的困难. 消除低频噪声，提高沙漠地震记录的信噪比是一个亟待解决的问题. 为了提高地震记录的信噪比，一系列信号处理的方法被应用于地震勘探随机噪声压制. 例如F-X滤波[1]、 小波去噪[2]、 经验模态分解(EMD)[3]、 时频峰值滤波(TFPF)[4]、 曲波变换[5]等. 然而，常规的方法由于其局限性，在处理沙漠地区低频随机噪声时不能取得有效的结果. 例如，F-X 域预测滤波要求反射波同向轴具有线性或局部线性，无法压制随机噪声，且去噪效果受信噪比约束，当某一频率成分的信噪比过低时很难求取准确的预测因子，从而导致信号严重失真； TFPF通常采用固定的窗长，这就导致某些有效的频率分量严重损失，信号的幅值可能会产生衰减和畸变； EMD分解很难将弱信号与强噪声分离，并且由于模态混叠问题对信号的保幅性存在严重影响. 小波变换具有更好的局部化特性，可以任意调节空间分辨率，对信号的特异性特别敏感. 小波变换能将信号时频率进行有效分解，并提取有效信息，在地震信号处理中也得到广泛应用. 但沙漠地区低频信号与噪声相互混叠，小波变换不能有效分离噪声与信号，且其滤波效果取决于阈值的选取，而小波分解层数的选取和去噪阈值的选取并没有确定的方法[6,7]. 随着神经网络的发展，其运用领域不断扩展，解决了其它模式识别不能解决的问题，其分类功能特别适合于模式识别与分类的应用. 多层前向BP网络是目前应用最多的一种神经网络形式, 它具备神经网络的普遍优点，例如非线性映射能力、 自学习和自适应能力、 泛化能力和容错能力，同时也存在一些较大的缺陷，例如收敛速度慢、 训练时经常陷入局部极小值、 网络结构选择不一等[8]. Zhang等1992年提出小波神经网络的概念，将小波分析理论与神经网络相结合，使其兼具小波分析优良的时频特性和神经网络的自学能力和鲁棒性. 小波神经网络是一种函数逼近拟合，所以一般的小波神经网络并不具有滤波的能力[9-11]. 将神经网络的非线性阈值单元和训练方法引入到小波去噪中，通过神经网络对标准样本的学习，能够较精确地确定该时段的去噪小波系数阈值，有利于阈值选取[12]. 本文将小波神经网络应用到地震勘探低频随机信号的压制中，能有效分离信号与噪声，提高地震记录的信噪比，为后续地质解释提供可靠的资料.

1 小波神经网络消噪原理

地震子波雷克子波如图1(a) 所示，是零位在中间的左右对称的零相位子波. 本文根据地震子波特性，选择Mexihat小波基及其尺度函数作为神经网络的激励函数，如图1(b) 所示，建立的小波神经网络结构如图2 所示.

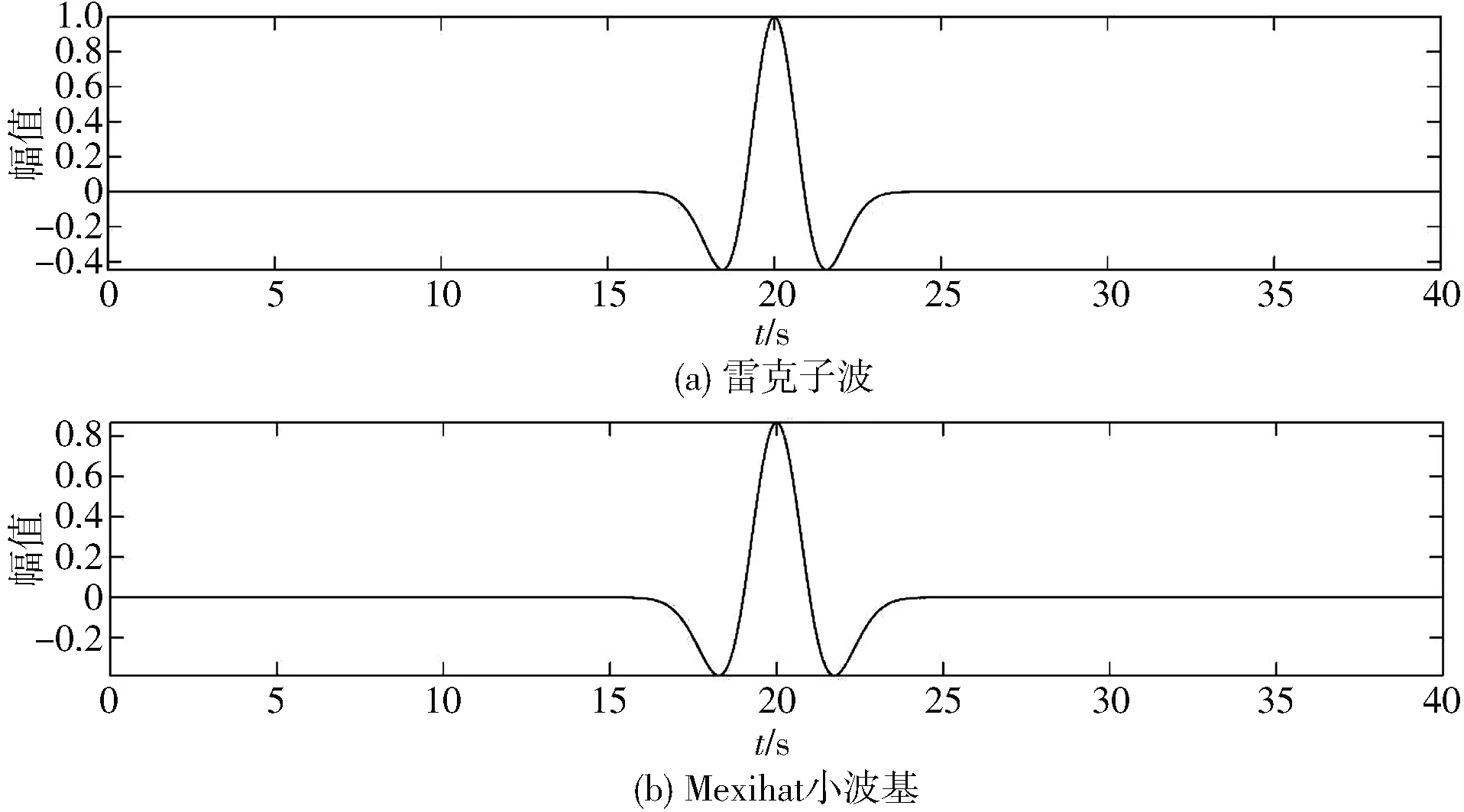
图1 时域波形图Fig.1 Time domain waveform (a)Mexihat wavelet basis

图2 小波神经网络结构Fig.2 WNN structure

输入层含一个神经元，其输入信号为含噪信号x(t).

输出层含有一个神经元，对阈值量化后的小波分解系数进行重构，输出去噪后的信号

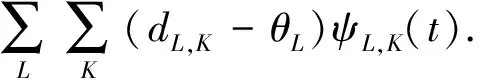
(1)

假设含噪地震信号可以分解为纯净信号和噪声信号，即

x(t)=s(t)+n(t),

(2)

式中：x(t)为含噪地震信号；s(t)为纯净信号；n(t)为加性噪声.

对小波神经网络进行训练时，需要分别对小波分解层数和阈值进行训练. 设神经网络的期望输出为纯净地震信号s(t)，其实际输出为y(t)，则网络的训练误差

(3)

式中：t为时间变量；τ为信号采样长度.

1.1 对神经网络分解层数进行训练

选择合适的小波函数. ① 根据地震子波(雷克子波)的形式选择Mexihat小波基； ② 输入信号的每一个小波分量设置多分辨率系数栅格. 当j=0时，分辨率最高，此时栅格间隔等于输入信号的采样间隔； 当j=L(L为小波分解尺度)时分辨率最小，此时栅格间隔等于两个数据间隔； ③ 将神经网络输入设为含噪信号x(t)，输出设为纯净信号s(t)，当j=L时，训练神经网络的神经元φL,K，若期望输出和实际输出的误差E不满足要求，则加入神经元ψL,K，直至误差满足要求为止. ④ 去掉K值特别小的神经元ψL,K，并设定新的输入，输出信号，重新训练网络模型，直至误差重新满足要求. 当神经网络再次稳定时，小波分解的层数已经训练完成.

1.2 对神经网络的阈值进行训练

假设神经网络阈值为θ，根据梯度下降法，调整幅度

(4)

式中：E为网络的训练误差.

调整过程为

θj(k+1)=θj(k)+ηΔθj,

(5)

式中：η(0<η<1)为调整系数.

通过不断循环迭代，调整θ使得网络的误差和最小，当E<ε时，停止迭代，神经网络的阈值θ训练完成.

当分解层数和阈值训练完成后，小波神经网络稳定，此时噪声n(t)的特征已经被网络记忆，网络输出的即为去噪后的信号.

2 应用研究

将自适应小波神经网络应用于地震信号处理中，分别用来压制人工合成记录和实际野外采集数据中的背景噪声，并将处理结果与地震信号处理中常用的小波去噪做对比. 在地震信号处理中，一般用信噪比和均方误差作为判断去噪效果的量化标准，信噪比越大，均方误差越小，去噪效果越好. 信噪比计算公式为

(6)

式中：N为离散时间点数；s(n)为网络期望输出，即纯净信号；y(n)为实际输出，即滤波后的信号.

均方误差计算公式为

(7)

为明确自适应小波神经网络对低频噪声的处理结果，先进行正演模拟，如图3 所示.

图3 人工合成地震记录Fig.3 Synthetic record

图3(a)为40道人工合成的纯净记录，其中包含3条有效同相轴，其主频分别为12 Hz, 20 Hz和30 Hz； 图3(b)为含噪记录，由纯净信号与背景噪声叠加而成，其中背景噪声为沙漠地区实际地震记录初至前噪声的截取，可以看出，背景噪声干扰较大，且噪声频率范围与同相轴主频相互混叠，信噪比低，在各个变换域内分离信号和噪声都比较困难； 图3(c)为小波去噪结果，可以看出，通过小波分解重构可以压制大部分噪声，但由于受分解层数和阈值选取的限制，有效信号也会被削弱，尤其是主频为12 Hz的同相轴频率与背景噪声相互重叠，几乎随着噪声一起被去除； 图3(d)为小波神经网络去噪结果，可以看出，背景噪声基本被压制，同相轴被清晰完整地恢复出来.

从图3 所示各记录中任意抽取单道记录进行对比(文中抽取第21道)，如图4 所示. 图4(a) 为单道时域波形对比图，可以看出小波神经网络处理过的信号几乎接近纯净信号，而小波去噪对有效信号的削减严重，尤其是第一个主频为12 Hz 的有效子波几乎被完全衰减； 图4(b) 为图4(a)中各时域波形的频谱对比，为了对比明显，幅值采用了对数坐标，同样可以看出小波神经网络处理过的信号频谱与纯净信号基本一致，而小波去噪信号频谱衰减严重，尤其是低频部分.

图4 单道记录对比Fig.4 One-channel record comparison

表 1 所示为各单道时域波形的信噪比和均方误差，可以看出含噪信号信噪比较低，均方误差较大，经小波神经网络处理后的信号信噪比得到了较大幅度的提高，均方误差明显减小.

表 1 单道记录去噪参数Tab.1 Denoising parameters of one-channel record

图5 所示为自适应小波神经网络应用于沙漠地区野外采集部分数据截取. 图5(a) 为原始含噪数据，背景噪声主要为低频随机噪声和面波(一种频率较低与有效信号相互混叠的线性干扰)[17]，干扰较强，同相轴被截断甚至湮没，信噪比极低. 图5(b)为小波去噪结果，框内的部分对比效果尤其明显. 图5(b) 可以看出，小波去噪法能够压制一部分随机噪声和面波，恢复出部分同相轴，但地震记录中信号和噪声在时频域内相互混叠，小波去噪法受分解层数和阈值选取的限制，不能将信号与噪声有效分离； 图5(c)为小波神经网络去噪结果，可以看出，小波神经网络可以压制大部分低频随机噪声和面波干扰，恢复出来的同相轴清晰连续. 图5 中1框区域放大图如图6 所示，图6(a)为含噪数据，由于低频随机噪声干扰，同相轴被截断甚至淹没； 图6(b)为小波去噪结果，可以看出恢复出部分同相轴，但去噪效果不是很明显； 图6(c)可以看出小波神经网络能够压制大部分的背景噪声，恢复出更多清晰连续的同相轴. 图5 中2框内可以看出小波神经网络能够去除面波干扰，恢复出连续的同相轴，提高地震记录的信噪比.

图5 野外采集地震数据

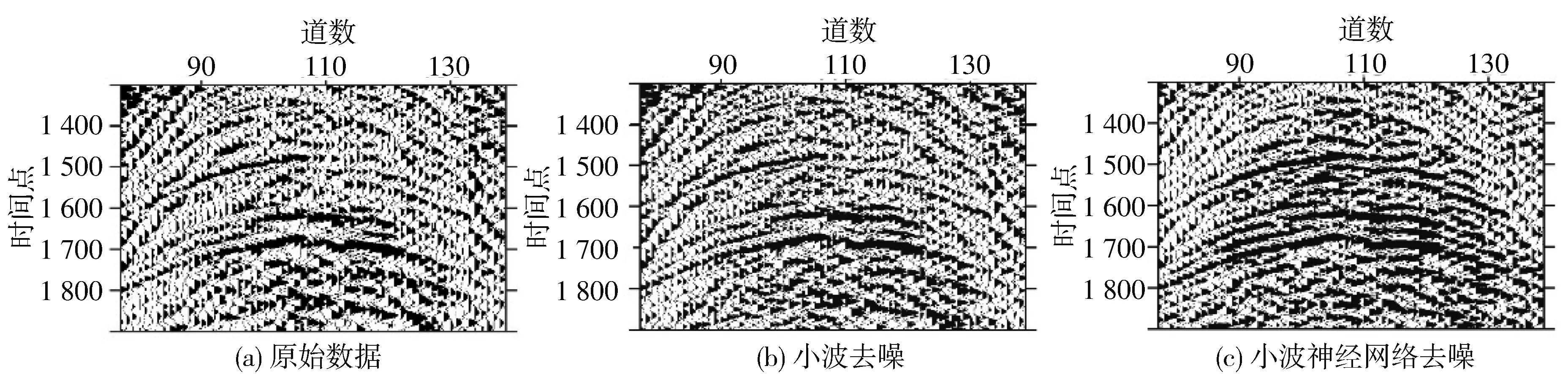
图6 图5框1中放大部分Fig.6 Magnified sections of red box 1 in Fig,5

3 结 论

本文提出了将小波神经网络应用到地震信号噪声压制中的方法，该方法能有效去除地震数据中的背景噪声，特别是针对与有效信号频率混叠的噪声，并且对面波也有很好的压制效果. 小波神经网络解决了小波分解层数的选择问题，更将小波重构过程中的阈值进行自适应选取，极大地改善了小波阈值选取的弊端. 将该方法应用于人工合成地震记录和野外采集数据，可以看出，该方法能够极大地提高地震记录的信噪比和分辨率，为下一步进行地质解释提供可靠的依据.