页岩油藏开发合理焖井时间数值模拟
张相春,杨亚静,刘军龙,高智席,黄小青,曾凡辉
(1.遵义师范学院 生物与农业科技学院,贵州 遵义 563006; 2.遵义师范学院 资源与环境学院,贵州 遵义,563006; 3.浙江油田分公司 勘探开发研究院,浙江 杭州 311100; 4.西南石油大学 石油与天然气工程学院,四川 成都 610500)
引 言
为了更好地对页岩油藏进行开发,水力压裂结合焖井渗吸的方式在各油田逐步得到应用[1-3]。针对微观尺度油水渗吸置换及其原理,许多学者进行了细致的实验与理论研究[4-8],然而矿场尺度的焖井作用机理研究则相对较少。目前,针对页岩油储层焖井增产机理的认识,主要分为两个方面,一是水力压裂结束后进行短期焖井,可以有效降低储层压裂液的返排率,促进压裂液与储层原油的相互置换,起到一定的增产效果[9-12]。其二,现场开发经验以及部分研究表明[13-15],合理的焖井措施可以有效地对储层的能量进行平衡,避免开井生产时储层能量的快速衰竭,使得油井产量快速下降,影响储层的长期有效开发。然而,目前页岩油储层压裂后焖井对产能的影响仍不明确,尤其是如何选取合理的焖井时间,最大程度提升油井经济效益,仍缺乏清晰的认识,亟需进一步的探索研究。
为了确定压裂开发页岩油藏的合理焖井时间,建立了包含毛管力的油水两相渗流、渗吸数学模型,通过与现场实际井的生产数据进行对比,验证了模型的准确性。以中国西南某页岩油藏Y区块Y-1水平井为例,进行了合理焖井时间优化。之后计算了不同物性储层5口生产水平井的合理焖井时间,并列出了其与流体黏度、裂缝渗透率、基质渗透率、毛管力大小等因素之间的关系,为现场实际开发提供一定的指导意义。
1 油水两相流动、渗吸模型建立
1.1 基本假设
将多级压裂后的页岩油储层分为2个流动区域,分别为未受压裂影响的基质区,以及受到压裂波及的SRV改造区域。模型采用如下假设:①储层渗透率按照预置分布,SRV区域渗透率远大于基质区域,储层上下封闭;②流体先由基质区流向SRV改造区,再由SRV改造区流入人工裂缝进而流入井筒;③流动过程为等温非稳态渗流,不考虑温度变化对于流动的影响;④模型为二维平面模型,不考虑重力作用,不考虑其他物理化学因素;⑤不考虑井筒储存和表皮效应;⑥垂直裂缝完全穿透页岩油储层;⑦为减小计算量,模型进行对称处理,只计算一半几何部分。
1.2 控制方程组建立
假设储层内部只有互不相溶的油水两相组分,则描述油相与水相的运动方程分别为[16]

(1)

(2)
式中:uo,uw分别代表油相和水相流速矩阵,m/s;kro,krw分别代表油相和水相的相对渗透率;po,pw分别代表油相和水相压力,Pa;μo,μw分别代表油相和水相黏度,Pa·s;k代表储层渗透率。
对于油相压力与水相压力,满足关系式
po=pw+pc。
(3)
式中:pc毛管压力,Pa。毛管压力曲线来源于实验室压汞实验测定后换算,实验样本来自于实际生产井邻近探井所取岩心。
油相、水相分别满足质量守恒方程[16]
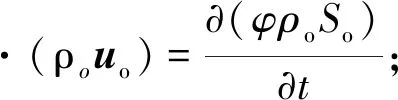
(4)
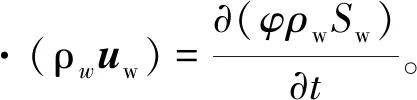
(5)
式中:ro,rw分别代表油相和水相密度,kg/m3;So,Sw分别代表油相和水相饱和度;φ代表孔隙度。
此外,油相、水相饱和度满足关系式
So+Sw=1。
(6)
方程组需满足初始条件
p|t=0=pi;
(7)
Sw|t=0=Si。
(8)
式中:pi是油藏初始压力,Pa,Si是初始含水饱和度。
1.3 注、焖、采边界条件设立
针对储层的外边界∂Ω1,注、焖、采过程中均设置为封闭边界条件
-n·ρu|∂Ω1=0
(9)
式中:n是外边界∂Ω1的法向量。
针对储层的内边界∂Ω2,即井筒处边界条件,注、焖、采过程中设置略有不同。
在注水阶段,边界条件∂Ω2设定为定流速且注入液体全部为水,即
(10)
Sw|∂Ω2=1。
(11)
在焖井阶段,边界条件∂Ω2设定为封闭边界条件,代表关井状态,即
-n·ρu|∂Ω2=0。
(12)
在生产阶段,边界条件∂Ω2在水平井处被定义为定压条件,代表以恒定井底流压进行生产,即
p|∂Ω2=pBHP。
(13)
式中:pBHP是恒定井底流压,Pa,
2 模型求解与验证
2.1 模型求解
方程(1)—(5)构成了页岩油藏油水两相渗流、渗吸的控制方程组[16],利用辅助方程(6)—(13),将方程组的关联变量消去,最终求解出不同时刻t的油相压力po与油相饱和度So,并换算得到水相压力pw与水相饱和度Sw。利用全隐式方法进行求解[17],在隐式求解中,将所求量压力及饱和度前面的系数都视作二者的函数,两个未知量同时放入方程组中,一并求解出来,没有显式求解过程,因此叫做隐式求解。该方法稳定性较好,计算精度较高。模型中裂缝需要进行离散化处理进行降维以方便网格划分。模型求解的基本步骤如下:①给出线性剖分各个节点的初始压力和各相饱和度等初始参数;②对控制方程的时间项和空间项分别进行离散化处理,把含求解变量的项移至方程左边,不含求解变量的项移至方程右边;③定义上游权原则对各项系数进行取值,通过初始条件和边界条件对离散方程进行条件限制,达西系数项和毛管力压力均采用上一时间步的值;④系数归项,排布二维条件下的对角矩阵;⑤进行矩阵运算,求解方程组,当相邻两时间步之间压力求解结果的差值小于固定误差值时,缩小时间步进的大小,重新计算该时间步;⑥重复循环计算直到两次计算结果差值小于计算误差限,跳出迭代,开始计算下一时刻的变量数值;⑦重复计算直到达到预定时间节点;⑧输出结果进行后处理。
2.2 模型验证
为了对计算模型的正确性进行验证,将模型计算结果与现场生产井实际生产数据进行了对比。在对比过程中,由于实际生产并非采用某一固定流压进行生产,动液面不断变化,因此在计算过程中,将产水量作为已知量进而计算产油量,通过对比产油曲线与井史数据是否吻合,判断模型是否具有相对准确性。对比验证计算参数如表1所示,对比验证结果如图1所示。

表1 对比验证模拟参数Tab.1 Simulation parameters for comparative verification
从图1结果可以看出,模型计算结果与现场实际产油数据基本一致,验证了模型的正确性。以上结果表明,模型用于计算页岩油藏压裂井油水两相渗流、渗吸过程足以满足计算精度要求。
3 实例分析与讨论
3.1 压裂水平井Y-1生产模拟
选取中国西南某页岩油藏Y区块作为研究对象,其储层和流体参数如表2所示。
表2中,毛管力曲线中位数是指岩心压汞实验所得的毛管力曲线,在汞饱和度为0.5时的毛管力大小,用于反映整体毛管力的大小。需要注意的是,压汞法所测得的毛管力数值与油层条件下油水毛管压力数值相差15倍,在数值模拟计算过程中需要通过换算才能使用压汞实验测试结果。SRV区渗透率分布为预置分布如图2所示,储层中渗透率最大值为50×10-3μm2。

图2 模型渗透分布及分区示意图Fig.2 Schematic diagram of reservoir permeability distribution and regional division in the model
为了对比不同焖井时间对生产井产能的影响,分别设计了不焖井、焖井40 d、焖井80 d、焖井120 d、焖井160 d的模拟方案,计算施工1 000 d(焖井+生产)后的累产油,通过对比不同方案的累产油大小,优选出该生产井的合理焖井时间。累产油曲线如图3所示。
通过图3可以看出,当不焖井直接生产时,累产油曲线与时间轴以一定角度相交。而随着焖井时间逐渐由0 d增加到160 d,交点处斜率逐渐减小,当焖井160 d时,曲线与时间轴近似相切,这说明生产初始时刻的产量随着焖井时间增加而减小。随着生产不断进行,不焖井的累产油曲线斜率逐渐减小,焖井方案的累产量逐渐超过不焖井方案。施工后1 000 d,焖井40 d与焖井80 d的累产油最多,二者产量近似相等,约为7 568 t。不焖井生产方案累产油最小,约为7 011 t。通过对比,焖井施工对于储层长期开发的积极作用得以体现。因此该区块Y-1压裂水平井存在最优焖井时间,约为40 ~ 80 d。
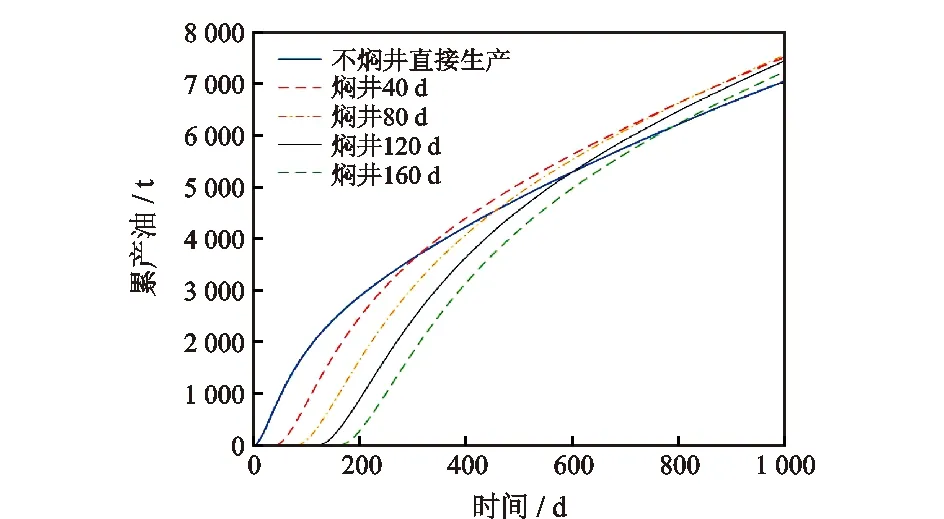
图3 不同焖井时间下累产油对比Fig.3 Comparison of cumulative oil production under different soaking time
值得注意的是,焖井生产的投资回报效益与压裂施工后的生产时间高度相关,如果生产时间过短,焖井不但无法产生增产效果,甚至可能致使生产井累计产量降低。图4展示了储层压裂施工后300 d,600 d,1 000 d不同焖井方案的累产油量对比。通过对比可以发现,生产时间300 d时,不焖井的累产效果更好;随着生产时间逐渐增加,焖井的时间成本逐渐得到回收,并产生显著增产效益。由此可知,焖井措施更适用于页岩油的长期生产过程。
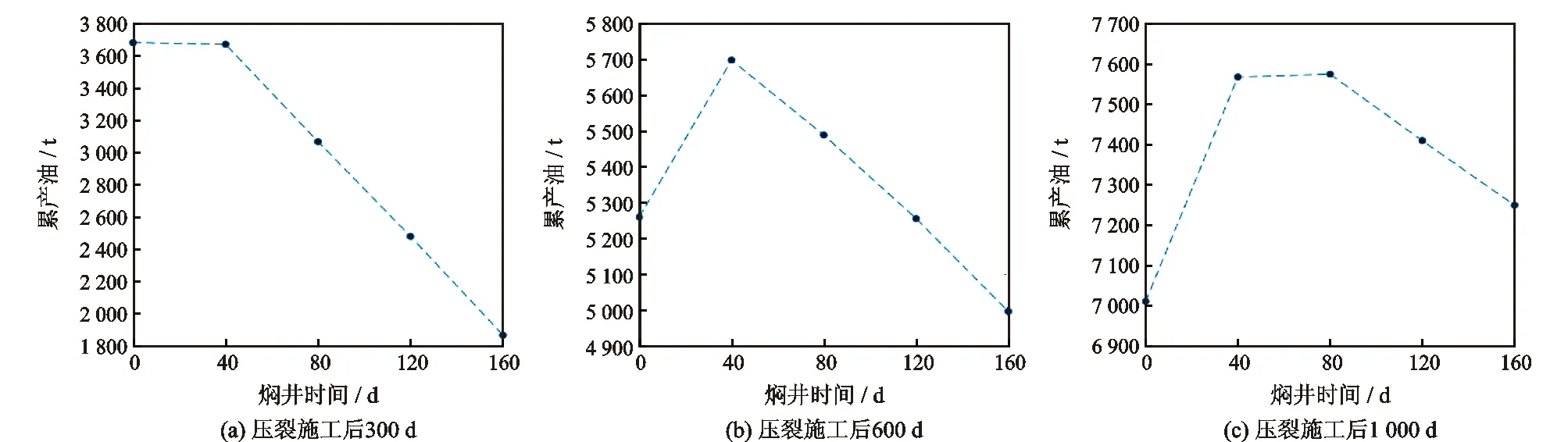
图4 压裂施工后不同时刻各焖井方案累产量对比Fig.4 Comparison of cumulative oil production of various soaking schemes after fracturing
此外还分析了焖井前后储层含油饱和度的变化。图5(a)为开始焖井时储层的含油饱和度分布,图5(b)为焖井80 d后储层的含油饱和度分布。通过对比可以看出,焖井开始时刻,水主要聚集在SRV改造区域内,而经过80 d的焖井施工后,在外部基质区较大的毛管力以及近井地带注水高压的驱动下,近井地带的水逐渐深入到了基质区域,储层内部发生了显著的油水置换现象,降低了储层的返排率,促进储层能量的补充,有利于储层的长期开发。
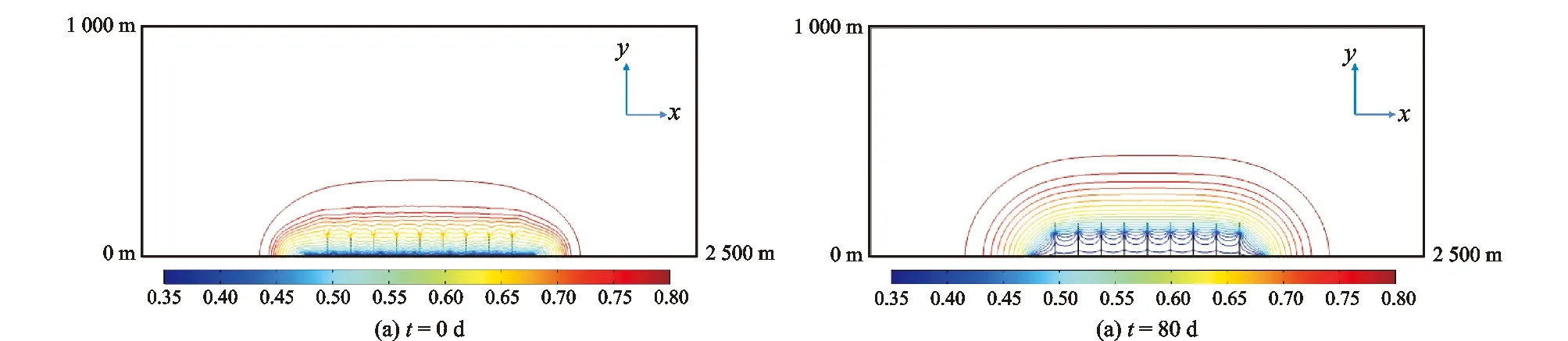
图5 焖井开始0 d与80 d后储层含油饱和度分布Fig.5 Oil saturation distributions in the reservoir at 0 and 80 days of soaking
3.2 不同储层参数合理焖井时间计算结果与分析
现场施工结果表明,不同物性储层其合理焖井时间各不相同。为了明确不同物性参数以及施工参数对于合理焖井时间的影响,选取中国西南某页岩油藏不同物性区块5口井Y-1,Y-2,Y-3,Y-4,Y-5进行合理焖井时间计算。5口井的物性参数、施工参数以及计算出的合理焖井时间如表3所示。

表3 Y区块5口井物性参数、施工参数与对应合理焖井时间Tab.3 Reservoir parameters,operation parameters and reasonable soaking time of 5 wells in Y block
通过对比可以发现,在相同注入液的情况下,合理焖井时间与储层油相黏度呈现正相关关系。这是由于油相黏度越大,油水黏度比越大,注入压裂液更易运移至储层深处,自发渗吸现象更加明显,这一结论与前人计算结果[18]相同。其次,合理焖井时间与渗透率具有较强的联系:其中,合理焖井时间与基质渗透率大体呈负相关关系,这是由于基质渗透率越小,其毛管力越大,焖井渗吸效果越明显;合理焖井时间与主裂缝渗透率大体呈正相关关系。此外通过对比可以发现,合理焖井时间与毛管压力具有较强的联系,对于毛管压力较大的储层,建议焖井时间适当延长,充分发挥渗吸引起的初期增产效果。现场实际应用时,应当针对不同物性储层设计对应的合理焖井开发方案。
4 结 论
(1)建立了页岩油藏油水两相渗吸、渗流数学模型,通过与现场实际生产数据进行对比验证了模型的正确性。
(2)随着焖井时间增加,初期产油量有所减少,后期产油则不断增加;最优焖井时间为40 ~ 80 d。
(3)合理焖井时间与油相黏度呈正相关,与基质区渗透率呈负相关,与SRV区渗透率呈正相关,与毛管力大小呈强正相关关系。

