基于区间线性规划和可逼近理想解排序法的园区型综合能源系统投资决策

张沛，王旭，杨璐，孙秋洁，叶玲节，王岑峰，冯也，杨云露，周竹君

（1. 北京交通大学电气工程学院，北京市 海淀区 100044；2. 山西大学电力与建筑学院，山西省 太原市 030006；3. 国网浙江省电力有限公司经济技术研究院，浙江省 杭州市 310016；4. 湖北泽电新能源科技有限公司，湖北省 天门市 431700；5. 武汉泽电新材料有限公司，湖北省 武汉市 430074）

0 引言

随着社会经济快速发展，能源需求的快速增长与能源日渐紧缺的矛盾日益凸显[1]。随着近些年经济的快速增长，我国的电力行业也在发展迅速，政府积极推进科技创新，鼓励能源转型，合理地构建综合能源系统可以协调运用多种能源，对能源进行梯级利用，进而提高能源利用率[2-3]。综合能源服务是以电力系统为核心，在投资、规划和运行的过程中，综合利用不同能源，有机协调多种不同能源之间的传输、转化、存储、利用等环节，达成能源高效利用的能源供应系统[4]。在电力市场化背景下，电网企业在综合能源服务项目的投资不断增加，同时社会资本的参与缩小了电网企业的盈利空间[5]。面对激烈的市场竞争，电网企业如何提升自身投资决策能力，在投资建设环节考虑多种不确定性因素，采用简单有效的决策方法从众多上报的综合能源项目中选取优质项目是十分值得研究的课题。

针对园区型综合能源系统投资决策方面的研究，其难点主要在于园区型综合能源系统的规划运行中存在大量的不确定性因素，譬如负荷预测误差、园区能源价格的波动及其他。若单纯地采用现有决策方法对园区型综合能源系统进行投资方案决策是不合理的，需要将园区的相关不确定因素与决策方法有机结合，形成计及不确定性的投资决策方法。目前，多数研究人员在对综合能源系统的不确定性因素方面已有一定成果。文献[6]提出了一种多微网互联系统的动态调度模型，并分析了风光、负荷等不确定性因素对动态调度模型的影响。文献[7]提出了一种基于模型预测控制的冷热电联供型(combined cooling heating and power, CCHP)微网动态优化调度策略，以应对大规模的新能源接入及负荷的不确定性。文献[8]基于能源集线器模型，采用鲁棒规划方法对负荷波动进行分析，进而确定其对冷热电多能负荷园区效益的影响。文献[9]提出了一种区域综合能源系统双层优化模型，考虑新能源出力和负荷不确定性的前提下采用粒子群算法对模型进行优化求解，最后根据优化结果量化分析了各类资源的不确定性对系统配置结果和系统盈利能力的影响。文献[10]对光伏出力及负荷的不确定性使用区间数进行描述，基于区间规划提出了一种综合能源系统日前经济优化模型，用区间形式体现最优解，并通过此最优解进而确定不确定因素对系统总收益的影响。以上文献虽采用不同方法对综合能源系统存在的不确定性因素进行了研究，进而推导出各不确定性因素对综合能源系统规划运行的影响。但并未将园区的相关不确定因素与现有决策方法有机结合，为园区提出一种具体的投资决策方法辅助投资者进行决策。

综上所述，为提升电网企业在综合能源系统项目的投资效益，本文从综合能源投资者角度出发，将园区规划和运行优化相结合，构建园区型综合能源系统技术优选模型，求解出一些经济性较好的投资规划方案；然后考虑能源购入价格和负荷的不确定性，对多个投资规划方案用可逼近理 想 解 排 序 法(technique for order preference by similarity to ideal solution，TOPSIS)，进 行 排 序，遴选出兼顾经济性和环保性的最佳方案。

1 基于区间数的综合能源系统不确定性规划模型

园区型综合能源系统可以有效整合不同能源，通过不同耦合设备间的协调工作，实现对能源的梯级利用，从而提高能源利用效率。园区的运营商从能源商处购置天然气、煤炭和电能，通过园区内部各种能源耦合设备的转换，满足园区能源负荷需求。

在实际的投资规划中，园区能源价格和冷热电负荷的预测均存在较大的不确定性，很大程度影响着投资者对园区型综合能源系统的投资决策。在能源交易背景下，能源价格与实时能源交易量有关联，具有一定波动性，一般来说也较难获取到精确的概率密度函数。在实际决策过程时，当不确定变量的取值范围获取易于精确的概率密度函数时，可采用区间规划法获得最优值区间。区间规划法在处理计及不确定性的能源规划问题时有其优点，尤其是不确定因素的精确分布情况获取困难时，可以采用区间数进行描述。

1.1 目标函数

1.1.1 全寿命周期成本

园区型综合能源系统的全寿命周期成本统筹考虑了各能源设备或系统的规划、选型、运行、维护和退役等在给定周期（即整个寿命周期）内发生的直接费用和间接费用的总和，因此本文提出的年综合成本 Coverall目标函数为

式中： Cinv为 投资成本； Cmt为系统维护成本；Coper为 系统运行成本；Cdep为折旧成本。

1）投资成本Cinv。

投资成本主要是指主要指园区型综合能源系统建设初期购置各类能源设备的成本和供能网络的建设费用，具体的计算公式分别为：

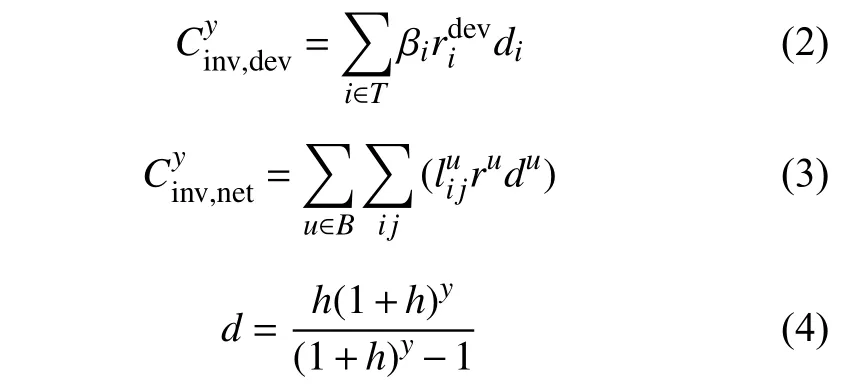
2）系统维护成本Cmt。

系统维护成本主要包括园区设备的维护成本和供能网络的维护成本，具体的计算公式分别为：

3）系统运行成本Coper。

系统运行成本包括能源购置费用和碳排放成本两部分。能源购置费用指系统从外部网络购买电能、天然气和煤炭的能源所花费的成本。

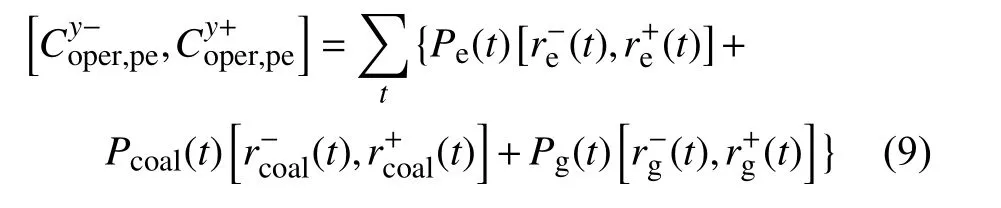
4）折旧成本Cdep。

折旧成本主要体现能源设备磨损损失价值的体现，本文采取固定的折旧费率进行计算，第y年的折旧成本为

式中： βi为选型系数；ri为 设备i的 成本价格； λi为设备i的折旧费率。

1.1.2 碳排放成本

由1.1.1节可知，全寿命周期成本已经包含了碳排放成本，可由式（8）求得，碳排放成本和全寿命周期成本呈现的是一种非线性关系，本文统筹兼顾园区的经济性和环保性，将碳排放成本提升到与全寿命周期成本同等的地位。

1.1.3 约束条件

本文构建的园区型综合能源系统规划运行联合优化模型的约束条件包含规划类约束和运行类约束两大类约束条件。其中运行类约束条件又由功率运行约束、设备运行约束和供能网络运行约束组成。

1）规划约束。

园区内各种能源的生产应该保证满足园区各类负荷最大负荷时的需要，这也是规划期从能源设备库内初步筛选能源设备的主要约束条件。具体约束条件如下所示：

式中： Te为可以产电为园区电负荷供给的所有设备的集合； Th为可以产热为园区热负荷供给的所有设备的集合； Tc为可以制冷为园区冷负荷供给的所有设备的集合；且 Te、 Th、 Tc均 为集合 T的子集； Wrate,i为设备i在额定工作方式下产出相应能源的能量；分别为电、热、冷最大需求负荷。

利用区间数来描述冷热电负荷的波动，即可将式（11）改为

2）运行约束。

①功率平衡约束。

在任一时刻，系统内的电、热、冷的功率平衡约束如下：

式中： Pi(t) 为 t时 刻设备i的 电出力； Hi(t)为 t时刻设备i的热出力； Ci(t)为 t时 刻设备i的冷出力；Le(t)为 园区t时 刻的电负荷； Lh(t) 为 园区t时刻的热负荷； Lc(t)为 园区t时刻的冷负荷。

同样地，用区间数来描述冷热电负荷的不确定性，可将式（13）改为

②设备运行约束。

园区内每个设备都有其运行特性，出力存在上下限，设备运行约束如下：

式中： Wi(t)为 t时 刻设备i的 出力；为设备i 的出力下限；为设备i的出力上限。

③供能网络运行约束。

对于电能传输网络在运行过程中，计算各个电负荷节点消耗的电功率时，需要将循环水泵工作时消耗的电功率考虑进去，因此各节点的有功和无功约束方程为

供热/冷网络的运行约束包括供热/冷负荷节点的换热器/风机的负荷功率模型，供水管道的温度约束和流量约束以及循环水泵的工作特性约束。

1.1.4 模型求解

求解算法采取两阶段分解算法，将包含不确定问题的模型转化成为确定性问题的子模型进行求解。区间线性规划模型一般形式为关键所在，首先构建标准化区间规划模型，其标准化过程见文献[11-12]；然后将构建的模型分解为最优子模型和最劣子模型。

1）求解最优子模型 ：

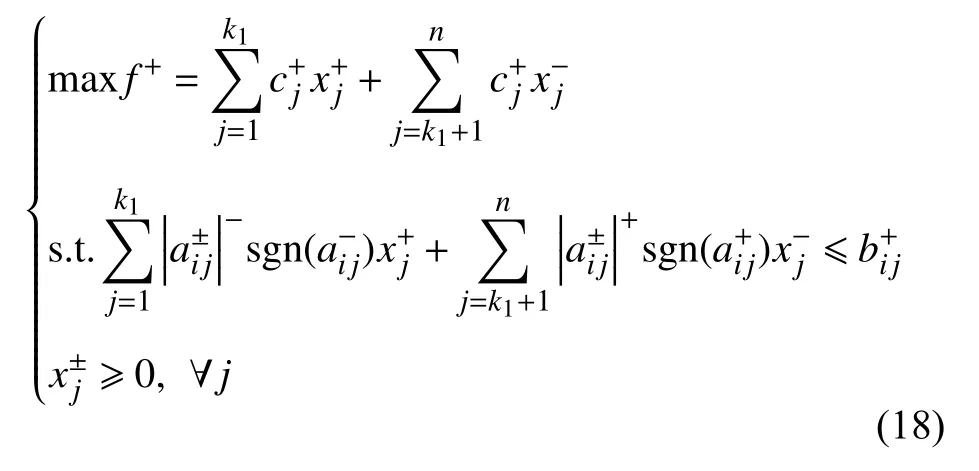
2）求解最劣子模型 f−：

最终对2个子模型的求解结果进行综合，求得模型的目标函数值以及决策变量

模型求解后，得到区间值年综合成本[Coverall]=和 年 碳 排 放 成 本以这2个区间值的均值表征园区的年均成本费用，并分别作为评价园区经济性和环保性的指标。

综上所述，基于区间数的综合能源系统不确定性规划模型的具体流程如图1所示。

图1 基于区间数的综合能源系统不确定性规划模型Fig.1 Uncertainty programming model of integrated energy system based on interval numbers

2 基于TOPSIS的园区型综合能源系统投资决策

TOPSIS法是目前被应用最广泛的多目标决策方法之一。TOPSIS法根据有限个评价对象与理想目标的接近程度对方案进行排序，进而优选方案。TOPSIS法是一种逼近理想解的排序法，其中“正理想解”和“负理想解”是该方法的2个基本概念。所谓正理想解就是理想中的最优方案，该方案的各个指标均达到备选方案中的最优值；而负理想解即是最劣方案，该方案各属性均为最差。该方法的基本原理就是计算出备选方案中的正负理想解，然后通过评价各个方案距最优解和最劣解的距离进行评价[13-14]。

TOPSIS法的基本计算过程为先将原始数据矩阵统一指标类型（一般正向化处理）得到正向化的矩阵，再对正向化的矩阵进行标准化处理以消除各指标量纲的影响。得到标准化矩阵后，从中得到“正理想解”和“负理想解”。再对各方案与正理想解和负理想解间的距离进行计算，得到各评价对象与正理想解之间的相对接近程度，从而确定各方案的好坏程度。TOPSIS法不限制数据分布及样本含量，方便数据计算。

采用TOPSIS 法对多目标综合评选具体流程如下：

1）假设有n个投资方案，其中每个方案包含2个评价指标，进而可以形成多目标决策矩阵F=(fij)n×2。

正向化处理决策矩阵，也就是让所有的指标都转化为极大型指标。反之对于极小型指标，指标越小越好，将其正向化处理的公式为

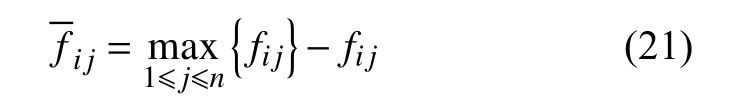
2）为了方便解决不同指标量纲之间的影响，标准化处理已经正向化的矩阵，形成标准化矩阵Z=(zij)n×2。

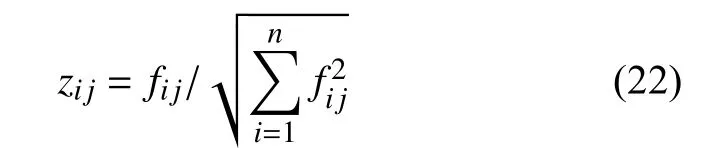
3）求得正理想解 Z+和 负理想解 Z−。

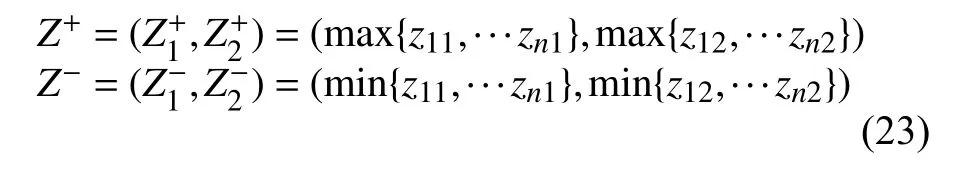
4）计算各个方案到正、负理想解的欧式距离 L+及 L−。方案i的欧式距离公式为

5）计算各个方案与理想点的贴近度S：

6）根据 Si的 值进行排序， Si∈[0,1]， Si值越小，代表该备选方案相对越差。

综上所述，基于TOPSIS法的园区型综合能源系统投资决策的具体流程如图2所示。

图2 基于TOPSIS的园区型综合能源系统投资决策Fig.2 Investment decision flowchart of integrated energy system based on TOPSIS

3 算例分析

3.1 算例场景

本文算例选取某个园区型综合能源系统，具体结构见图3。该园区的供热网、供冷网均包括12各管道和13个节点；供电网络采用IEEE14节点算例，基准功率为100 MV·A，基准电压为23 kV，包括13条支路。为了保证供冷/热网络正常运行，在所有的冷/热源节点处和冷/热负荷节点处安装循环水泵。园区供冷网的冷源供水温度为6 ℃，冷负荷回水温度温度12 ℃。园区供热网的热源供水温度85 ℃，热负荷回水温度30 ℃。水泵扬程为最高30.6 m，水泵的效率为0.8。该系统供能网络的具体参数见附表A1—A3。

图3 园区型综合能源系统结构图Fig.3 Structure of Integrated Energy System for industrial park

本算例构建的候选设备库具体参数详见附表A4—A10。为满足园区冷热电负荷需求，园区的运营商将从上述设备库中选择合适设备，通过园区内部各种能源耦合设备的转换及协调运行，实现对能源的梯级利用。

为简化分析，对一年8760 h的冷热电需求场景进行聚类回归并，将一年分为夏季/冬季/过渡季节3个典型的季节，以典型日的运行情况来代表整个季节的运行情况以减少运行模拟的计算量。各典型日的具体划分情况如表1所示。该园区聚类归并后各典型日的负荷曲线详见附图A1。

表1 典型日分类情况Table 1 The classification of typical days

该园区电价采取分时计价，峰时（08:00—10:00和18:00—22:00）、平时（07:00和11:00—17:00）、谷时（01:00—06:00和23:00—24:00）电 价 分别 为0.9640、0.6785、0.4090元/(kW·h)。园区购置天然气的价格折合成单位热值单价为0.34元/kWh，购置煤炭价格折合成单位热值单价为0.11元/kWh。为了提高园区的环保性，考虑碳排放成本，碳税为0.3元/kg，天然气和煤炭的碳排放系数分别为0.4和0.9。考虑到规划年内不确定性的因素，将负荷的波动设置为−5%和+10%，能源价格的波动设置为±10%。

3.2 技术优选结果分析

首先，以算例中的设备库参数为基础，根据排列组合可知，不同设备不同类型互相组合形成不同的规划方案，总共有220=1048576种方案。根据公式(9)，以满足园区最大负荷需求为硬性条件筛选出满足负荷需求的备选规划方案集Q，共包含8640种方案。因此该园区规划阶段设备选型的初步筛选率为 ε =(8640/1048576)×100%=0.82%。

然后，结合上述计算结果，根据不计及区间数的模型对备选规划方案集Q中每个方案Qi(i=1,2, ···,8640)进行运行优化计算。以年综合成本最小为优化目标，得到备选规划方案集Q中第3664种方案Q3664为联合优化的最优规划方案Qbest。最优规划方案Qbest设备选型的结果为Qbest=[1,1,1,1,1,0,1,0,1,1,1,1,0,0,0,1,0,1,1,1]，即该园区具体的规划方案为：燃煤锅炉3台(240 kW/350 kW/560 kW)、燃 气 锅 炉2台（350 kW/480 kW）、热电联产机组2台（250 kW/750 kW）、热泵机组3台(6 kW/20 kW/53 kW）、吸收式制冷机组1台(2910 kW)和电制冷机组3台(18.5 kW/114.6 kW/40.8 kW)。

为了进一步对比分析园区型综合能源系统年成本费用的构成，本文除了选取联合优化得到的最优规划方案Qbest之外，还从备选规划方案集Q中选取年投资成本最小的方案Qinv和年运行成最小的方案Qoper进行联合对比分析，具体对比结果见表2。

通过表2中园区型综合能源系统3种不同规划方案的成本费用的对比分析，可以得到以下结论：1）园区型综合能源系统的年成本费用主要受到园区负荷和能源价格的影响；2）碳排放成本作为运行成本的主要组成，其数额的大小体现了该综合能源系统环境的友好程度；3）通过3个不同方案对比分析可知，成本费用最低的方案碳排放成本未必最低，碳排放成本最低的方案，其经济性不是最优。由此可见，能源价格和园区负荷是影响园区投资决策的两个因素。

表2 不同方案费用对比Table 2 Costs comparison among different cases 万元

3.3 计及不确定性的投资决策结果分析

为进一步考虑到园区负荷和能源价格的波动对园区投资决策的影响，并兼顾综合能源系统投资的经济性和环保性，从技术优选求解得到的备选规划方案集Q中选取8个备选方案作为本节算例，其中包括3.2小节中提及的3个典型方案：Qbest、Qinv和Qopr。园区内负荷的波动为−5%和+10%，能源价格的波动为±10%，根据公式(1)—(19)，得到计及不确定性的园区型综合能源系统技术优选模型的区间优化形式。采用两阶段分解算法求解，得到各方案年成本费用和碳排放成本的最优值区间，具体结果见表3。

表3 区间优化模型求解结果Table 3 Results of the solving of interval optimization model 万元

以年综合成本和碳排放成本的区间均值表征园区的年均成本费用，并分别作为评价园区经济性和环保性的指标。由于经济性和环保性指标均属于极小型指标，需要对这2类指标按照式(21)进行指标正向化处理。指标正向化后的投资方案评价表见表4。

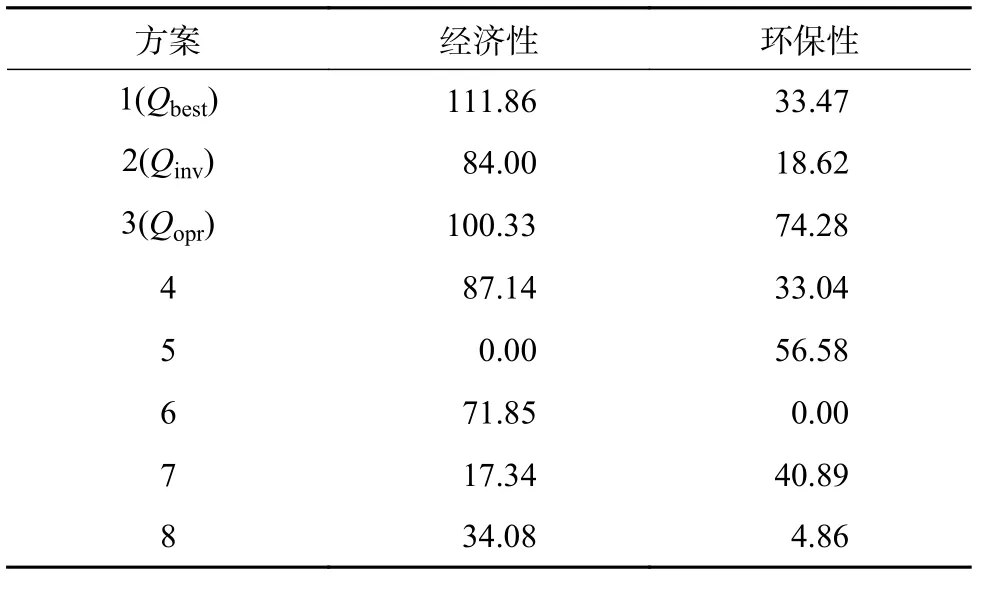
表4 指标正向化后的投资方案评价表Table 4 Appraisal form of investment plan after indicators normalized

依照式(22)进行标准化处理后得到的标准化矩阵如表5。

根据式(23)得到正、负理想解分别为：Z+=(0.5342,0.4968)、 Z−=(0.0000,0.0000)。

依据式(24)计算各个方案到正负理想解的距离 Li+及 Li−， 然后根据式(25)计算贴近度 Si并对方案进行排序，具体结果见表6。

表5 投资方案的标准化矩阵Table 5 Standardized matrix of investment plan

表6 投资方案的相对贴近度及排名Table 6 Relative closeness and ranking of investment plan

由此可见，贴合度最高为方案3，此方案同时统筹了经济性和环保性，所以是最佳的投资方案。通过采用上述投资决策方法，不仅考虑了园区型综合能源系统的不确定性因素，还从众多备选方案中评选中最佳投资方案，给投资方提供更明确投资辅助。

4 结论

1）在进行园区型综合能源系统的投资决策过程中，追求经济性最佳的同时，对环保性的考量是十分必要的。经济性较优的方案，其环保性较差；环保性不错的方案，其成本费用可能略高。若单纯只考虑园区经济性或环保性去遴选方案均不太合理。统筹兼顾经济性和环保性才能更好地对园区型综合能源系统进行投资规划。

2）本文所提的基于TOPSIS的园区型综合能源系统的投资决策方法将优选模型和方案评选结合起来，求解满足园区的投资规划方案的同时，进行方案间比选，操作简单，既兼顾了园区的经济性和环保性，又直观地展示了各个方案之间的相对差距，给投资方提供更明确投资辅助。

（本刊附录请见网络版，印刷版略）