基于概率积分法的采空区残余变形对桑掌隧道的影响研究*

李金洋 臧明东 徐能雄 秦 严 陈 宇

(中国地质大学(北京)工程技术学院， 北京 100083， 中国)

0 引 言

煤炭资源是经济发展与社会进步的重要物质基础。煤炭开采使得地下矿体形成空洞，围岩的原始应力平衡被打破，导致围岩应力重分布(马凤山等， 2018)，造成上覆岩层及地表剧烈破坏，岩层发生变形、开裂、破碎与冒落，形成大量采空区。采空区不但破坏范围广、变形量大，而且变形持续时间长。采空区岩层的残余变形持续时间可达数年甚至数十年(郭广礼， 2001)，对上方构筑物危害巨大。以往遇到采空区通常采取避让的方式，尽可能不去触碰涉及多层采空区的建设场地。然而，随着我国公路铁路网的不断加密，尤其在山西等煤炭生产大省，越来越多的交通隧道不得不穿越采空区(张永波等， 2007； 段丽军等， 2017)，采空区造成隧道衬砌结构变形破坏以及路面和路基下沉成为公路建设中的常见问题(叶懿尉等， 2018)。如何有效评价采空区残余变形对隧道的影响成为穿越采空区隧道工程建设的关键。

1956年，波兰学者Litwiniszyn(1956)提出随机介质理论来研究岩层移动规律。随机介质理论将矿山岩体视为不连续介质，由刚性颗粒组成，则岩层的移动可视为刚性颗粒在重力作用下向下方开采空穴的移动过程。20世纪60年代初期，刘宝琛等(1965)在随机介质理论(Litwiniszyn， 1956)的基础上解算出其简化解，提出了概率积分法，实现了从理论方法到应用的发展，成为目前我国预计地表沉陷的主要方法(姜岳等， 2019)，后来也被广泛用于采空区地表残余沉降的预计。刘天泉等(1995)通过研究给出了基于概率积分法的裂隙带高度计算方法。余学义等(1997)编译了评价采空区对公路影响程度的概率积分法程序。李仁民等(2002)对概率积分法进行改进，提出了适用于多层采空区的地表沉陷预测方法。陈晓斌等(2007)建立了基于随机介质理论的采空区地面变形计算模型，并编制了相关计算程序。王磊等(2011)和朱广轶等(2014)提出了概率积分法等价变采厚计算模型。蔡音飞等(2016)提出了概率积分法的优化方法，将概率积分法应用于起伏地表的采空区残余沉降计算中。李亚兰等(2018)基于随机介质理论，推导出了半圆拱形断面巷道开挖引起地表下沉和水平位移的计算公式，为深部工程的规划设计提供了参考依据。

概率积分法在采空区地表及岩层残余变形预测方面已经得到广泛应用，但在预测穿越采空区隧道的残余变形方面鲜见报道。本文以穿越山西省阳泉二矿采空区的新建桑掌隧道为案例，引入玻兹曼函数对等价变采厚概率积分法中的边界空洞残余可活化厚度进行修正，并引入时间函数对该地区采空区残余变形进行了预测，分析了残余变形对桑掌隧道建设的影响。研究成果可为隧道工程建设提供方法支撑。

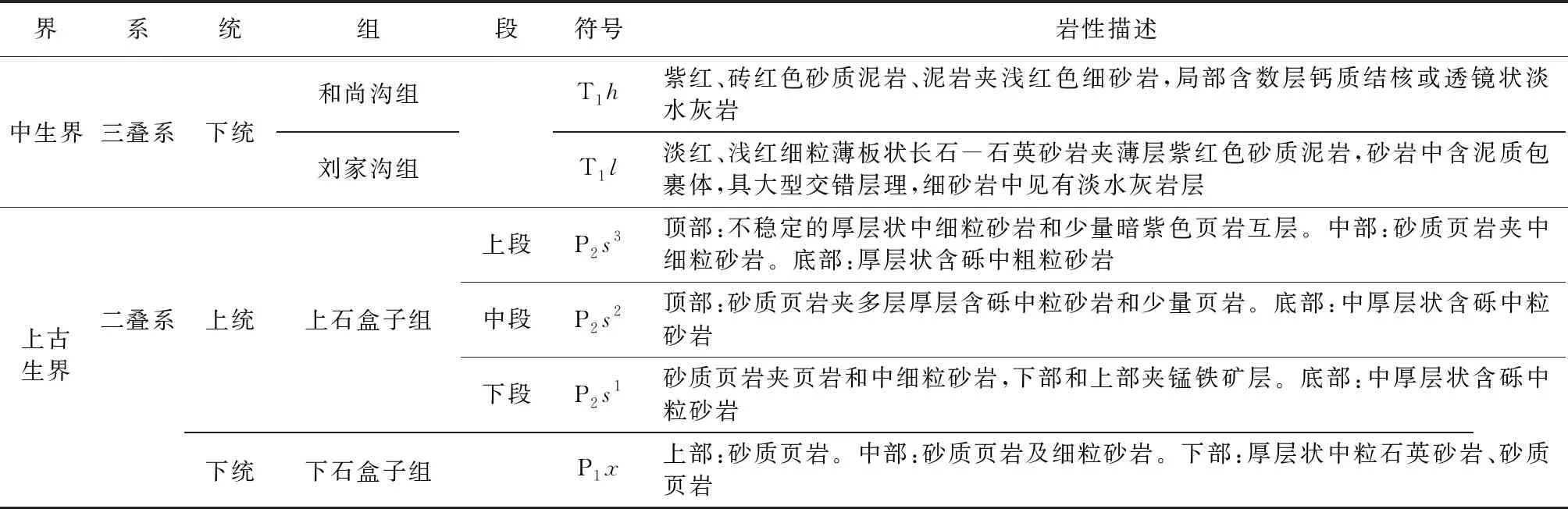
表1 项目区地层岩性描述表

1 研究区地质背景及工程概况

1.1 区域自然地理及工程地质条件

阳泉二矿矿区位于山西省东部的阳泉市西南部郊区，所选研究区位于阳泉二矿西北部(图1)，该区受内陆高原、暖温带季风气候带的大陆性气候影响，四季分明，干燥多风，十年九旱，年平均气温为10.8℃，多年平均降雨量为572mm，雨量集中在7、8两个月，降水量达340mm，占年平均降水量的66.4%。区内植被具有一定的垂直分布特征，冲洪积平原和山间河谷区以草甸植物群落为主，低中山区以木本、草灌植物群落为主。

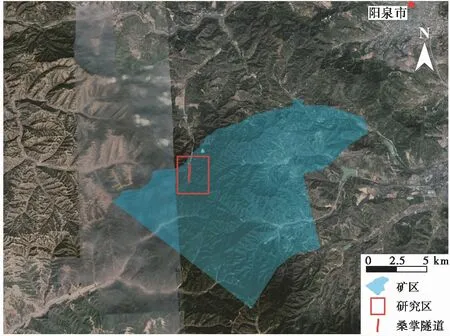
图1 研究区位置(据GoogleEarth卫星影像修改)

矿区地处太行山中部，整体地势西高东低，平均海拔1000m，相对高差约540m，呈典型的构造剥蚀地貌。在构造和长期剥蚀切割作用下，形成了山脉纵横、峰起峦连、沟谷深切的地貌形态(图1)。如图2所示，区内出露地层主要为三叠系下统和尚沟组(T1h)的砂质泥岩夹长石砂岩和刘家沟组(T1l)的长石砂岩夹砂质泥岩以及二叠系上统上石盒子组(P2s)和二叠系下统下石盒子组(P1x)的砂岩、页岩、泥质砂岩、砂质泥岩及泥岩(表1)。

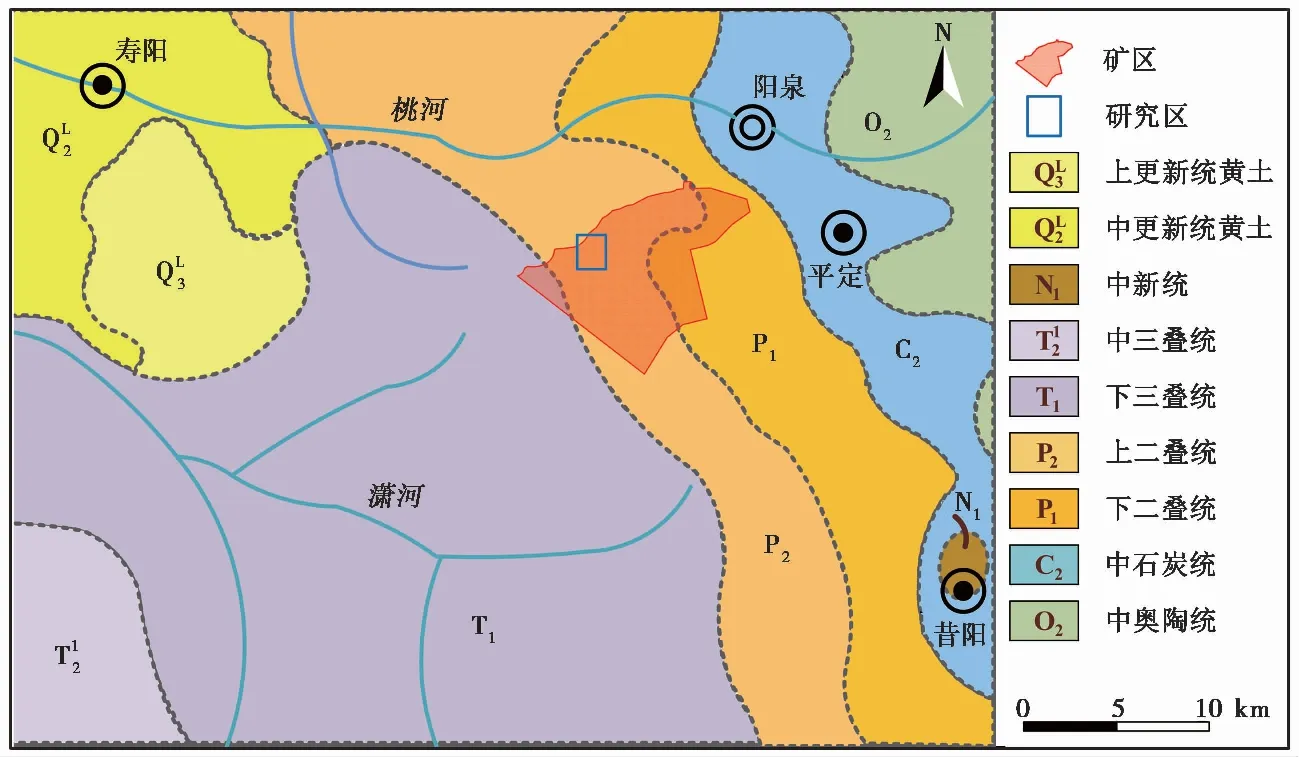
图2 研究区区域地质图(据马丽芳(2002)修改)

1.2 工程概况

阳泉二矿建矿于1951年5月，井田位于沁水煤田东北部，面积约60.06km2。阳泉二矿煤层稳定，赋存丰富，剩余服务年限30年以上(山西省交通规划勘察设计院， 2016)。煤矿开采深度463.3～713.5m，主要可采煤有3#、8#和15#煤层，平均厚度分别为1.96m， 2.26m以及6.42m，采煤方法为综合机械化放顶煤开采，属走向长壁后退式采煤法，顶板管理为全部垮落法。其中： 3#煤层工作面回采率98.6%， 15#煤层工作面回采率88.5%。新建桑掌隧道位于研究区中部(图3)，全长925m，平均埋深80m。隧道从上石盒子组下段地层穿过，距离3#、8#和15#煤的平均垂直高差分别为275m、320m和400m(图4)。由于3#和8#煤层的工作面停采时间较长，对隧道影响较小，因此本文主要研究15#煤层的工作面对隧道的影响。隧道主要受15#煤层的4个采煤工作面影响(图3)。其中： ①号工作面位于隧道起点东南侧，工作面长轴方向与隧道近似平行，该工作面于2019年9月停采； ②号和③号工作面沿长轴方向与隧道小角度相交，分别于2017年9月和2015年4月停采； ④号工作面位于隧道东侧，沿长轴方向平行于②号和③号工作面，于2012年3月停采。

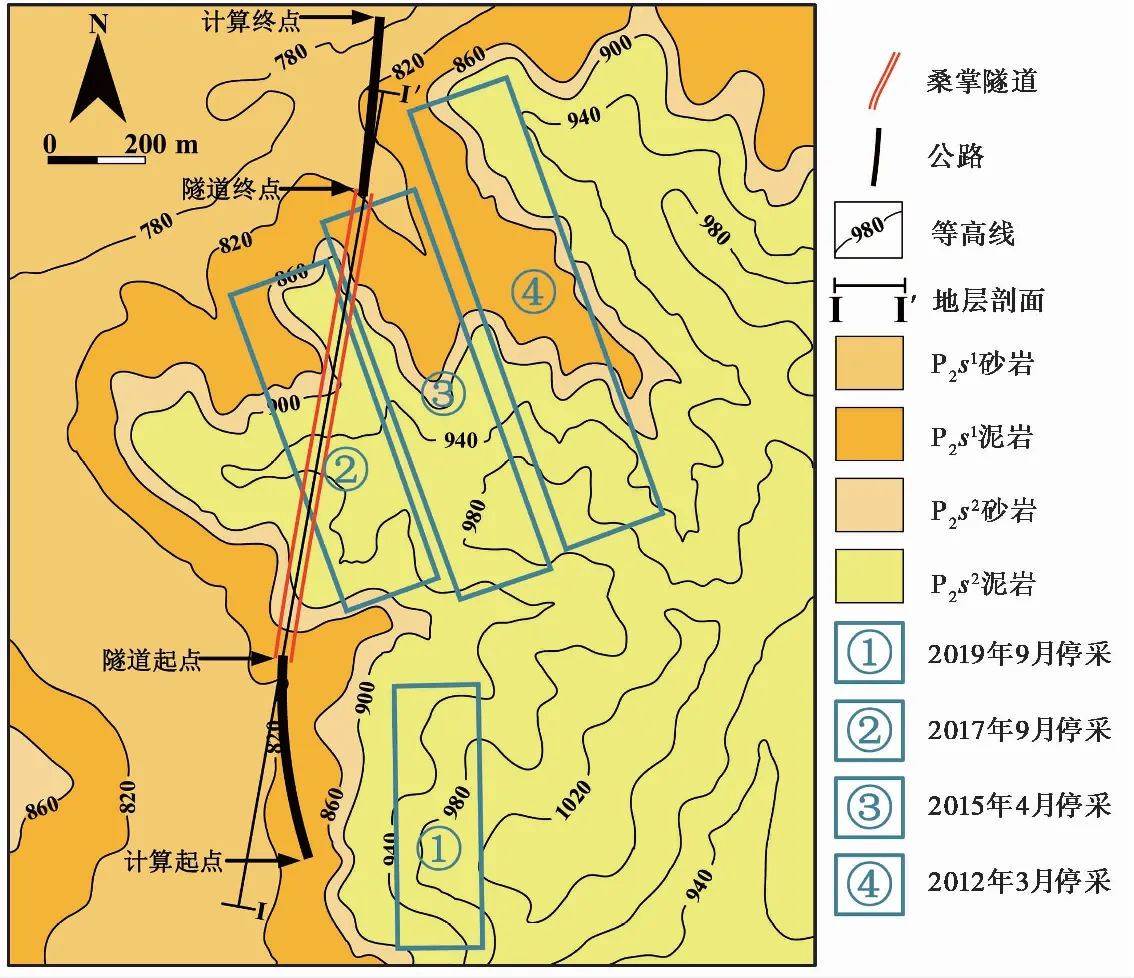
图3 研究区工程地质平面图(地层符号含义见表1)

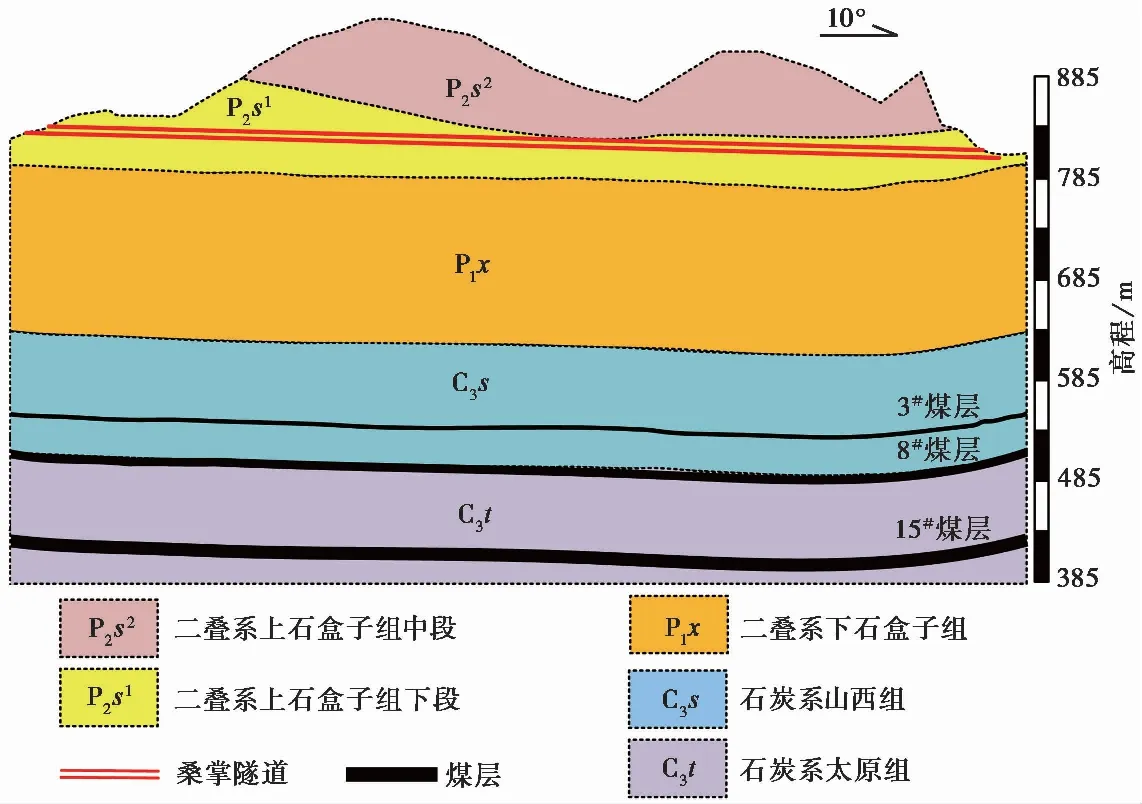
图4 I—I′剖面图(剖面位置见图3)

2 计算方法

2.1 计算模型

本文采用等价变采厚的概率积分法模型(王磊等， 2011； 朱广轶等， 2014； 图6)对隧道轴线所在平面的残余变形进行计算，利用玻兹曼函数对边界区残余可活化厚度进行修正。同时，引入Knothe时间函数(Knothe， 1952)建立残余下沉量与时间的定量关系，用于综合考虑停采历史不同的工作面在同一时刻的残余变形量。

2.1.1 改进的等价变采厚概率积分法模型

如图5所示，煤层开采后上覆岩层依次形成垮落带、断裂带和弯曲带(郭广礼等， 2002)。在垮落带内，岩体破碎，由于边界处的岩梁作用，自老采空区边界至采空中央具有明显的分区性：空洞区、未充分压实区和较充分压实区(王磊等， 2011； 朱广轶等， 2014)。针对长壁后退式开采形成的老采空区活化引起的地表残余沉降，从老采空区的覆岩形态结构出发，采用等价变采厚的概率积分法模型(王磊等， 2011； 朱广轶等， 2014)进行计算：

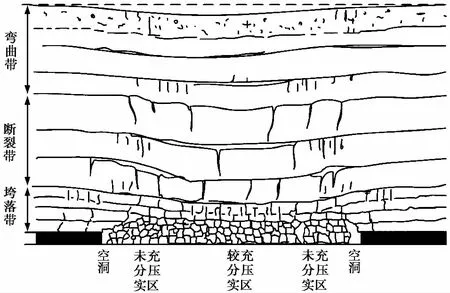
图5 采空区覆岩结构示意图(郭广礼等， 2002)

(1)

m1=m(1-q)

(2)

(3)

式中：W0(x)为残余沉降最大值；x为地表任意点的横坐标；s为开采单元的横坐标； AC、CD、DB为积分区间(图6)；m′与m1分别表示边界区与中部区残余可活化厚度；We(x)为单元开采形成的单元下沉；m为采厚；q为残余变形刚要出现时刻的地表下沉系数；r为影响半径。

如图6所示，由于采空区边界空洞区残余可活化厚度是线性变化的，等价变采厚的概率积分法在此处无法积分，前人在计算时常根据采厚m进行简单估算(王磊等， 2011； 朱广轶等， 2014)，但此假定与边界空洞区实际情况不符，会造成边界区残余变形量比实际允许的残余变形量大，导致地表残余变形量的预测偏大。鉴于边界空洞区实际上为非充分沉陷，本文采用玻兹曼函数对边界区残余可活化厚度进行修正，计算方法为：

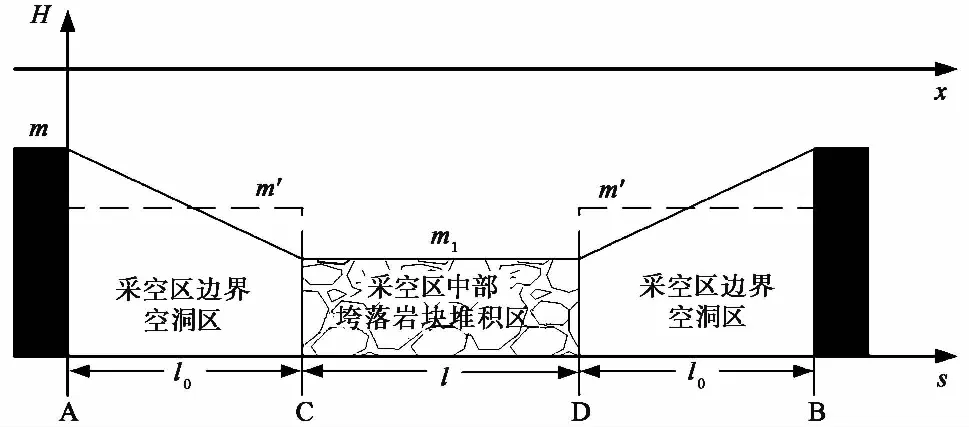
图6 等价变采厚的概率积分法模型示意图(据朱广轶等(2014)，郭庆彪(2017)修改)

m′=m[1-qρW(kL)]

(4)

其中

(5)

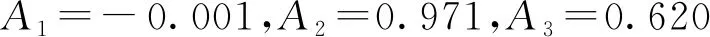
2.1.2 基于时序的残余变形预测模型

采用上一小节所述方法，虽可获得开采后地表残余变形的最大值，但是残余变形随时间变化的中间过程并不清楚。Knothe时间函数(Knothe， 1952)作为开采沉陷预测中常用的时间函数被广泛用于描述地表动态下沉过程(王文学等， 2017)。因此，本文引入Knothe时间函数(Knothe， 1952)来刻画地表下沉量与时间的关系：

W(x，t)=W0(x)(1-e-λt)

(6)

式中：W0(x)为残余沉降最大值，可由式(1)求得；λ为与上覆岩层力学性质相关的时间因素影响系数。

将式(1)～式(5)带入式(6)中，可以得到基于时序的残余变形预测模型：

(7)

2.2 参数选取

采用概率积分法对采空区上覆岩层与地表的残余变形进行预测时，计算参数的选取是关键。根据《建筑物、水体、铁路及主要井巷煤柱留设与压煤开采规范》，计算参数可以根据采空区覆岩的岩性进行选取，如表2所示。

表2 覆岩参数表(国家安全监管总局等， 2017)

根据现场勘察，新建桑掌隧道下伏采空区为3层采空区，采空区埋深463.3～713.5m。其中隧道下伏3#煤层和8#煤层与隧道的平均垂直高差分别为275m与320m，这两层煤的停采时间均超过10年，因此，在计算时可将下伏多层采空区看作重复采动情况，进行相应的参数调整(国家安全监管总局等， 2017)。下伏15#煤层与隧道的平均垂直高差为400m，煤层倾角较小，可近似看作0°。15#煤层覆岩为砂岩、泥岩和粉砂岩，根据表2，覆岩类型为中硬，经计算，非充分沉陷率ρW(kL)=0.81。据艾亚民等(1990)对阳泉地区煤矿的长期观测与工程实践，阳泉地区充分采动的下沉系数为0.85，重复采动情况下，下沉系数为q=0.85+0.1±0.05，本次计算下沉系数取q=0.92，其余计算参数如表3所示。

通过对时间函数的分析可知，参数λ的值越大，时间函数会在越短的时间内趋于一个定值。由于压实区会先于空洞区完成残余变形，所以压实区的λ取值一般大于空洞区的取值。结合阳泉矿务局对二矿周边矿区参数λ选取的经验，本区内参数λ的取值如表4所示。

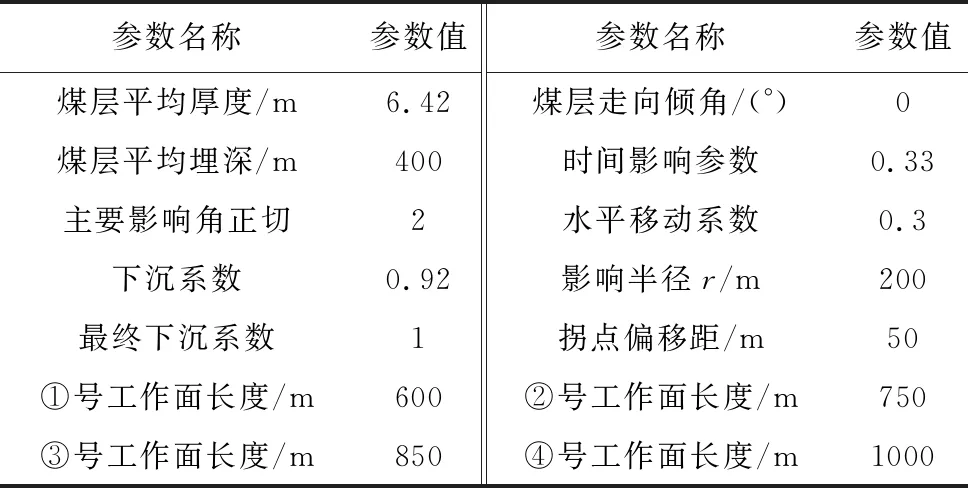
表3 计算参数表

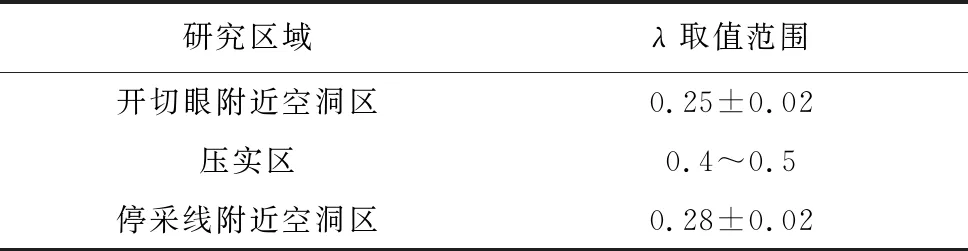
表4 时间影响参数λ取值范围

3 采空区残余变形预测

首先，采用上节所述方法对阳泉二矿一工作面停采后293天的累积沉降量进行试算，预测的最大沉降量为140mm，与实测数据145mm相近(孙富强， 2018)。因此，本文提出的预测模型具有一定的可靠性，可用来对本研究区内采空区的残余变形量进行预测。

将表3所示的计算参数代入式(1)，通过分区及积分叠加的方法计算各工作面停采后的最大残余变形量。其中：工作面沿开采方向的最大残余沉降量和最大残余水平移动如图7所示，垂直开采方向的最大残余沉降量和最大残余水平移动如图8所示。工作面停采后地表最大残余沉降量为647mm，最大残余水平移动为255mm。

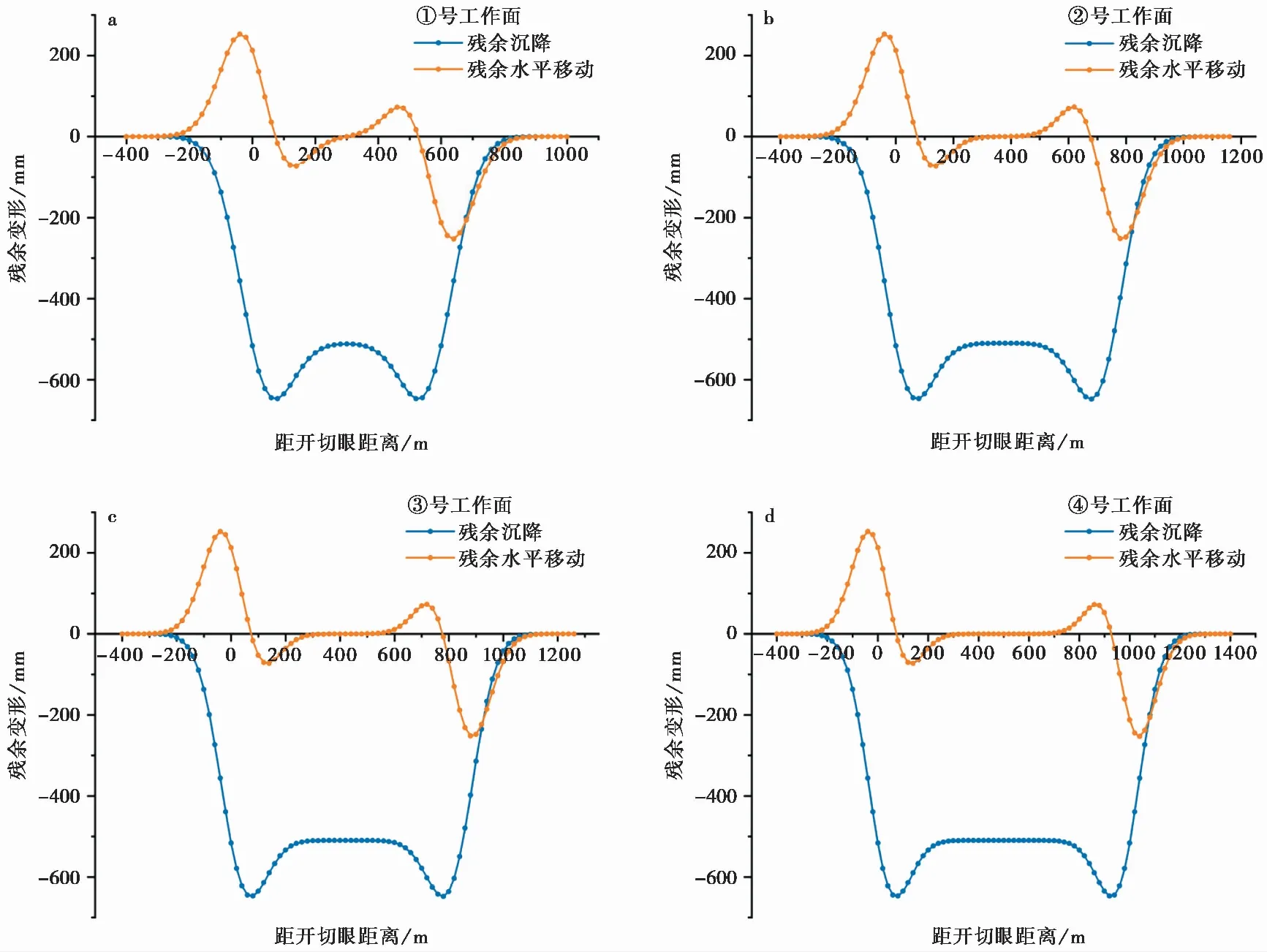
图7 沿开采方向工作面残余沉降与残余水平移动

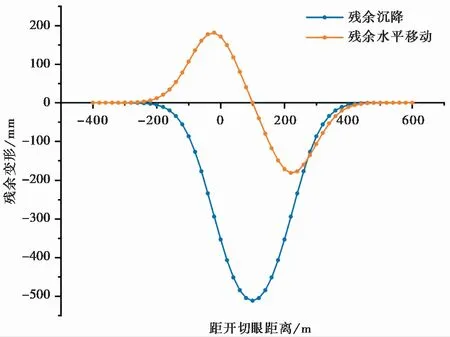
图8 ①～④号工作面垂直开采方向残余沉降与残余水平移动

如图3所示，桑掌隧道受4个工作面影响。隧道起点距离②、③、④号工作面较远，在一定范围内只受到①号工作面的影响。隧道中段部分穿越了②号和③号工作面的上覆岩层，同时也受到①号和④号工作面的影响。4个工作面的停采时间各不相同，因此，采空区残余变形对隧道的影响需要同时考虑工作面停采时间和工作面影响范围两个因素。

首先，考虑工作面停采时间这个因素。如前所述，本文已经通过式(1)计算出了4个工作面停采后潜在的最大残余变形量。在此基础上引入时间函数，并认为采空区变形总量为煤层厚度，即最终下沉系数为1。隧道开挖时， ①、②、③、④号工作面已分别停采1年、3年、5年和8年，通过式(6)计算得到各工作面在2020年之后在隧道轴线所在平面的残余变形量。

然后，考虑工作面影响范围这个因素。由于4个工作面距离较近，相互之间会有影响。针对区域内一点，通过对单个工作面影响下的残余变形进行叠加获取该点的累计残余变形量，并据此做出隧道轴线所在平面的残余沉降等值线(图9)。

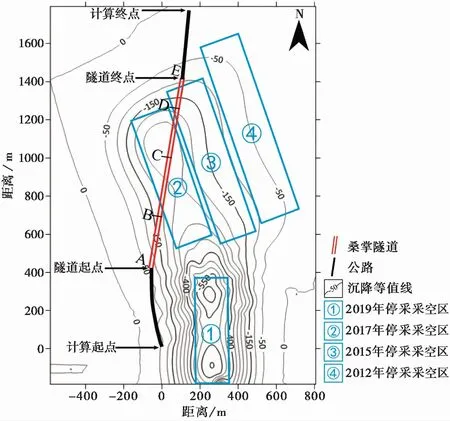
图9 隧道轴线所在平面残余沉降等值线图

沿隧道轴线做剖面，可得隧道沿轴线方向上的残余沉降，如图10所示，以及隧道沿轴线方向上的残余水平位移，如图11所示。其中：残余水平位移可分为垂直于隧道轴线方向和平行于隧道轴线方向两个方向的水平位移(图11)。

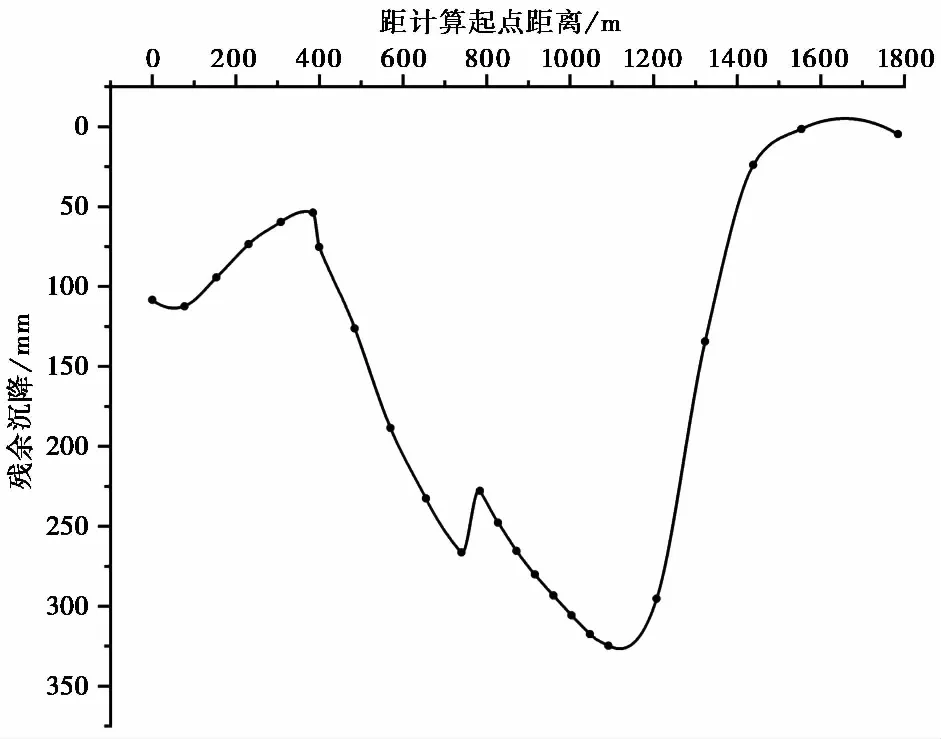
图10 隧道残余沉降(计算起点见图9)

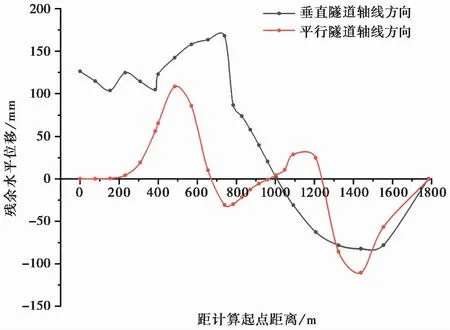
图11 隧道残余水平位移(计算起点见图9)

4 采空区残余变形对隧道的影响分析

通过对比图7和图8可以发现，沿开采方向，工作面残余沉降呈“W”型，工作面残余水平移动呈起伏波动的形态，两者最大值均出现在开切眼与停采线附近的空洞区，而工作面中部的较充分压实区残余变形量相对较小。这主要是由于采用长壁垮落法开采时，开切眼与停采线附近出现了空洞区，致使其潜在可沉降空间较大。垂直开采方向，工作面残余沉降呈“V”型，工作面残余水平移动亦呈起伏波动形态，其中前者最大值出现在断面中心位置，而后者最大值出现在靠近边界的位置。这是由于垂直开采方向的悬空跨度较小，竖向变形集中发生在中部，而侧向位移集中出现在边界位置。

由图9可知， ②、③和④号工作面沿开采方向平行展布，工作面残余沉降较为集中地出现在②号工作面上方，在隧道轴线所在平面内潜在的最大沉降量为325mm。②、③和④号工作面停采较早，采空区沉降历史相对较长，各工作面残余沉降量较之①号工作面偏小。由于①号工作面停采时间只有一年，沉降不充分，残余沉降量较大，在隧道轴线所在平面内潜在的最大沉降量为617mm。由于②、③和④号工作面距离较近，相互之间有影响，因此该区域内残余沉降等值线图的形态与①号工作面存在较大差异。而①号工作面距离其他3个工作面较远，采空区变形相对独立，同时，可以看出计算得出的①号工作面残余沉降呈现分区特征(图9)，边界区残余沉降较大而中部较充分压实区残余沉降较小，这与前人的研究结果是一致的(张永波等， 2010； 王磊等， 2011； 朱广轶等， 2014； 郭庆彪， 2017； 陈怀玉等， 2019)。

由图10可知，隧道的最大残余沉降出现在隧道中段，残余沉降量为325mm。由隧道中段向隧道两端，残余沉降逐渐变小，并在隧道起点和终点处达到最小，残余沉降量均小于100mm。在隧道前段(740m附近)出现了一个残余沉降的“局部峰值”(图10)，产生这个“局部峰值”的原因在于，隧道在此处从②号工作面边界的上方穿过，采空区的边界空洞区相较于中部较充分压实区具有较大的残余沉降，而整个隧道的最大残余沉降出现在②号工作面的另一边界上方(1150m附近)，该处除了受②号工作面边界空洞区的影响，还叠加了③号和④号工作面的影响，使得残余沉降达到最大。

由图11可知，在隧道轴线平面内，沿隧道轴线和垂直隧道轴线两个方向，残余水平位移均呈现起伏波动的形态。在隧道起点和终点附近均存在较大的残余水平位移，最大可至168mm。因隧道与②号工作面的长轴方向呈小角度相交，隧道侧向位移空间较大，因此在垂直隧道轴线方向上隧道的位移更为明显。隧道残余水平位移最大值出现的位置与残余沉降“局部峰值”出现的位置基本相同，可以推断，这两者形成的原因是一致的。对比图10和图11可以发现，在残余沉降最大的位置，残余水平位移并不明显。这是因为该处的位移受到②、③和④号工作面的共同影响，残余沉降由3个工作面引起的沉降叠加形成，而水平位移因其引起的位移方向不同而产生互抵。

根据隧道受采空区残余变形影响后的潜在状态将其分成AB、BC、CD和DE 4段(图9)，各段的变形特征如图12所示。在垂直隧道轴线方向的水平位移方面，由于AC段和CE段的潜在水平位移方向相反，隧道将产生一定的弯曲变形，呈“S”形态； 在平行隧道轴线方向的水平位移方面，AB段和CD段具有向北的位移趋势，而BC段和DE段具有向南的位移趋势，这导致隧道在B点和D点附近将产生较大的压缩变形，而在C点附近将产生较大的拉伸变形； 在沉降变形方面，隧道整体呈下沉趋势，但沉降并不均匀。沿AC方向隧道的潜在沉降量依次增大，沿CE方向则依次减小，最大沉降将出现在C点附近。同时，由于隧道与沉降等值线斜交(图9)，沉降中心并不在隧道的正下方，因此隧道将产生一定的轴向扭转变形。需要指出的是，图12展示了隧道的变形趋势，并不代表隧道的真实变形量。

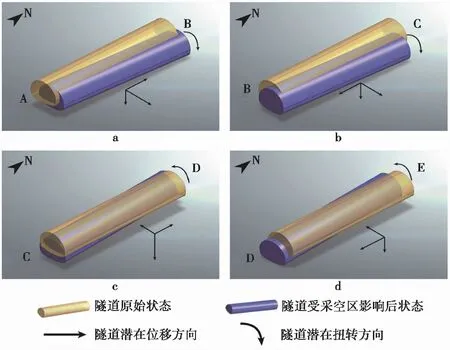
图12 隧道变形特征分段示意图

综上所述，虽然②、③和④号3个工作面停采时间较早，各工作面的残余沉降空间有限，但由于三者距离较近，相互之间存在影响，加之隧道从它们上方穿越，所以三者对隧道变形和长期稳定性的综合影响较大； 同时由于隧道与上述3个工作面的长轴方向呈小角度相交，隧道与残余沉降等值线斜交，因此隧道的变形发生在多个方向上，受力状态复杂，呈现侧向移动、竖向下沉与轴向扭转的复合变形趋势。相反地，尽管①号工作面的残余沉降较大，但由于其与隧道距离较远，工作面长轴与隧道近似平行，隧道与工作面残余变形等值线近似平行，因此①号工作面对隧道变形的影响较为单一而且范围有限。

5 结 论

现有的变采厚概率积分法模型在进行边界空洞区参数选取时，将采厚m看作边界区的残余可活化厚度，导致地表残余变形量的预测值偏大。本文通过煤层上覆岩层岩性和工作面参数，采用玻兹曼函数确定边界空洞区参数，对边界残余可活化厚度进行了修正，同时引入时间函数，构建了基于时序的残余变形预测模型，利用该模型计算了桑掌隧道穿越的4个停采时间不同的采空区在2020年之后的残余变形量，并分析了其对桑掌隧道长期稳定性的影响，取得如下认识：

(1)工作面残余沉降沿开采方向呈“W”型，在垂直开采方向呈“V”型，而工作面残余水平移动均呈起伏波动形态。

(2)新建桑掌隧道线路上潜在的最大残余沉降量和最大残余侧向位移分别为325mm和168mm，分别位于隧道中段和隧道起点附近。

(3)隧道的长期稳定性受②、③和④号工作面的影响较大，受①号工作面的影响相对较小。隧道的变形呈现出侧向移动、竖向下沉与轴向扭转的复合变形趋势。

(4)将时间函数引入概率积分法可以使停采时间不同的采空区在时间尺度上统一，消除沉降历史的差异性，以便于多采空区综合影响下残余沉降的预测。本文的计算方法可以为分析采空区残余变形对隧道的影响提供参考。