基于泛在电力物联网的用电行为特征解析与应用研究

戴晖， 秦镜， 程帅

(国网淮安供电公司，江苏 淮安 223001)

0 引 言

随着国家市场经济的不断发展，电力体制改革进程也在不断深化。对电力企业经营和发展而言，电力市场分析工作显得愈发重要。伴随城市地区电网高速发展，电力系统的负荷发生了很大变化，出现最大电网负荷持续快速增长、负荷峰谷差增大、电网负荷率下降、检修季节部分设备停运时电力供应紧张和电网调峰难度越来越大等一系列现象，加剧了电力供需矛盾，也给电力负荷分析预测、电网规划和业扩报装工作带来许多困难[1-2]。另外，对于用电客户的业扩报装要求，提出新装用电和增加用电申请，受理并确定能够满足用户要求的供电方式，是电网规划部门的一项重要工作[3-4]。本文结合不同区域用户类别调研，对用户用电特性进行分析。

1 基于泛在物联网的用电行为特征解析架构设计

本文以泛在物联网为中心，将各个地区的用电智能终端、传感器和物联网等集合起来，实现不同地区、不同用户用电行为数据的分析和应用[5]。架构示意图如图1所示。

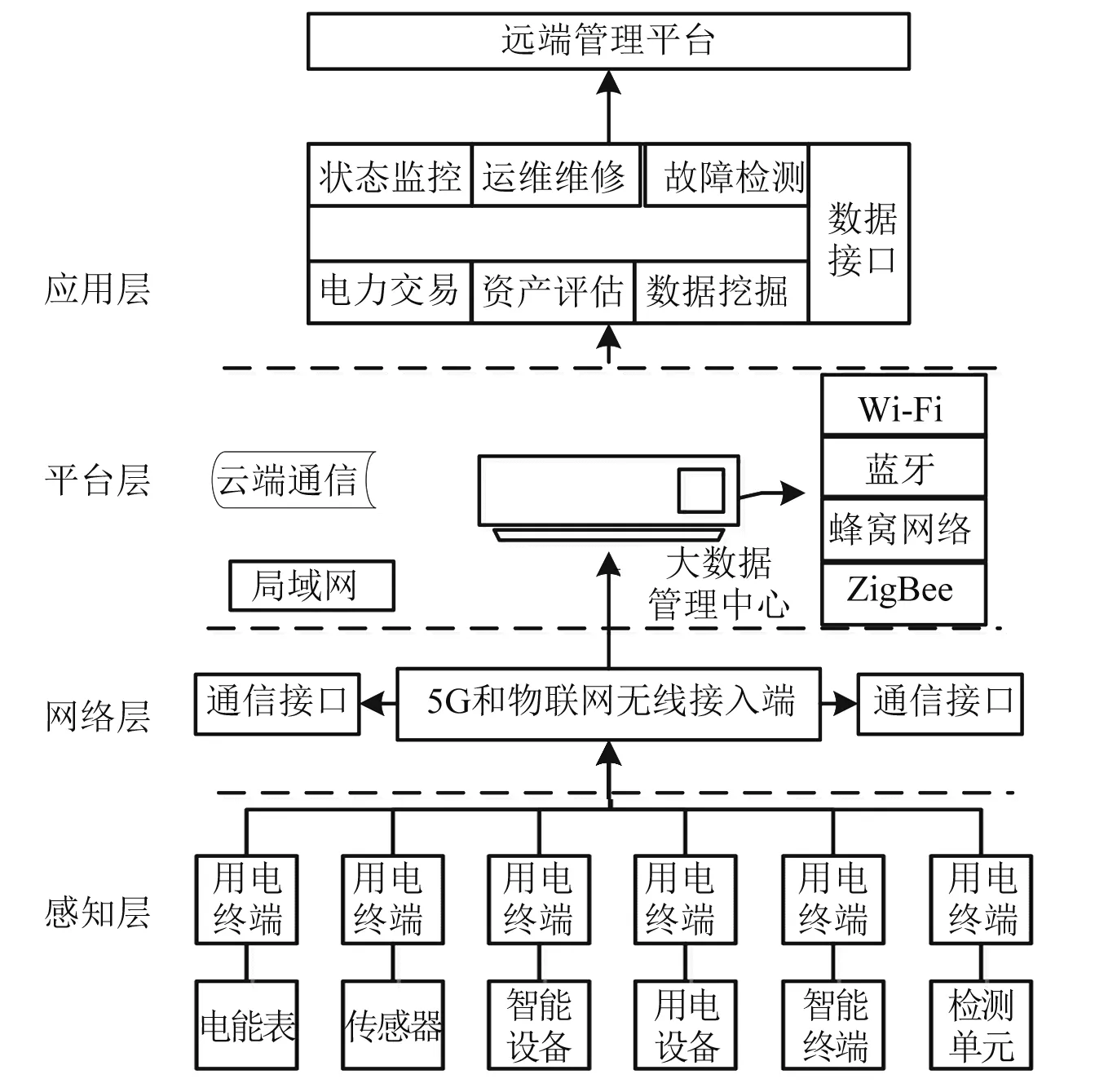
图1 泛在物联网的用电行为解析架构示意图

本文的技术创新点在于以下几点：

(1) 构建出集合多种信息的物联架构系统，在感知层感知用电信息，在网络层传递用电信息，在平台层实现多种信息分析和应用，在应用层实现数据的多种应用，进而实现物联通信。

(2) 将不同区域和不同行业的用电信息集合起来，通过大数据分析技术实现各种不同区域和用户的用电信息分析，能够跨越时空和区域实现数据的信息互联，并具有泛在连接、数据感知、大数据融合和共享等新型特点[6]。

(3) 在大数据统计分析技术原理的基础上，再次应用灰色算法模型，对用户用电行为进行预测。通过拟合曲线将统计出的大数据信息直观地表达出来，进而实现不同地区和不同用户的用电行为分析，大大提高了用户用电效率，提高了用户用电的监控力度。

2 关键技术设计

2.1 基于MEA算法和BP神经网络的多源数据融合算法

本文采用MEA算法来确定BP神经网络初始权值和阈值，从而快速得到最优的用电信息数据融合模型[7]。MEA算法是一种采用迭代进化方式的学习方法，它在遗传算法的“种群”和“进化”思想的基础上提出了“趋同”和“异化”两种操作[8]。“趋同”是在子种群Si(i=1,2,…,n)中快速找到局部最优子种群，i表示不同种群中的某个种群。对各个子种群局部环境信息进行快速检索和打分，通过分数来确定局部最优，最优个体Ni,pbest的得分就是其所在子种群Si的得分；“异化”则是在整个解空间内搜索子种群，对分数较高的子种群予以保留，对分数较低的子种群进行剔除。同时为了保证子种群的总数不变，在解空间内随机产生新的子种群。这样经过不断地进化，最终得到的子种群为最优子种群。

MEA算法可以用来优化初始权值和阈值、学习规则和网络结构，本文将其用来确定BP神经网络的初始权值和阈值，提高BP神经网络的精度和稳定性。采用MEA算法来确定BP神经网络的初始权值和阈值的方案如图2所示。

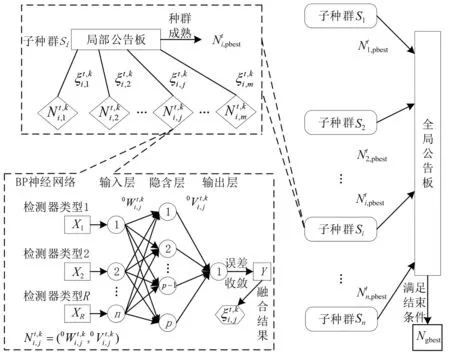
图2 MEA算法和BP神经网络融合结构

图2中:t为MEA算法中当前时刻正在进行的迭代循环次数;k为某个子种群内部当前时刻正在进行的迭代循环次数。从图2可以看出，BP神经网络的初始值和阈值的确定方式用子种群内部的某一个体来替换，在各个子种群内部进行迭代过程。通过局部公告板筛选出局部最优个体，然后将所有种群内部的最优个体通过全局公告板进行进一步比较，筛选出全局最优个体和最优子种群，最终采用全局最优个体代表的初始权值和阈值训练得到BP神经网络模型医疗信息数据融合模型，即医疗信息数据融合模型。

整个模型的关键部分是得到子种群内部的最优个体，在子种群内部进行迭代，以通过局部公告板得分最高的个体为中心进行收缩，直到子种群成熟为止。

将子种群Si内部的个体看作正态分布:

Ni(μi,Ci)

(1)

式中:μi为正态分布的中心向量，在本研究中为子种群内部的最优个体的位置坐标；Ci为正态分布的协方差矩阵，因为BP神经网络的初始权值和阈值之间没有互相影响，所以Ci可以看作对角矩阵。

Ci=diag(σ1,σ2,…,σd，…，σk)

(2)

式中:d为整个解空间中所有个体的维数。

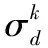
作为“大哥”的“雪龙号”有着出色的成绩单：1994年10月，第一次奔赴南极，执行南极科考和物资补给运输任务，此后一直参与极地的各种科学考察任务，已奔赴南极35次；对北极，“雪龙号”也毫不陌生，从1999年开始，它已经先后9次造访过北极。

(3)

式中:Hd为子种群内部第d维个体的上限;Ld为子种群内部第d维个体的下限。

当迭代次数达到设定的次数,或者五次迭代的正态分布的中心向量，也就是最优解的位置坐标没有变化的时候，就认为子种群达到成熟状态，此时最优个体的得分即为子种群的得分。然后将所有子种群的局部最优解进行迭代计算得到全局最优解，全局最优个体的初始权值和阈值则作为本文中用电信息数据融合模型的初始权值和阈值。

2.2 基于灰色GM(1,1)模型的大数据分析技术

(4)

针对上述x(1)输出的一阶均值，可以导出序列值xi，二者之间存在以下线性关系：

(5)

在式(5)中，k≥2。

对上述线性方程进行微分求解，得出以下函数关系式：

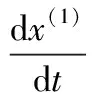
(6)

式中:a为用电终端或者场合；u为用电方式，通过这种方式可以求出a和u之间的关系，可以输出用户在特定环境下的用电特征分析。在求该值时，需要借助于最小二乘法，最终要应用的公式可以为：

(7)

然后进行数据还原，则有：

(8)

(9)

式中:k≥1。

通过上述公式，能够实现用户在不同阶段和区域用电量的精准预测、量化预测。

3 试验结果与分析

为了验证上述数据融合算法的有效性，在试验室内采用计算机仿真进行验证，其中计算机的硬件配置CPU为Inter Core i7-9700H，运行内存为3 200 MHz 8×2 GB，硬盘大小为1 TB。

选取2018年淮安市一年中食品、饮料和烟草制造企业的用电数据为试验数据，对数据进行统计，可以得到如表1所示的试验数据。

表1 试验数据

将前6个月的数据作为训练样本，训练收敛后对后面6个月的用电量进行预测，最后与真实值进行对比。首先对上述收集到的数据进行预处理，处理方式主要是对错误的数据进行剔除、对缺失的数据进行补充以及数据的降噪处理。本文采用的数据融合模型的网络参数设置如表2和表3所示。

表2 数据融合模型算法的网络参数设置

表3 算法网络结构设置

采用上述数据对本文的数据融合算法和传统的BP神经网络数据融合算法进行对比。将本文算法的数据融合结果与100次BP神经网络的数据融合结果进行对比，可以得到图3所示两种算法的收敛性对比。

从训练误差的最低位置来看，本文算法的训练误差要小于BP神经网络，因此本文算法的收敛性要比BP神经网络的要好。同时在图3中可以很明显地看到BP神经网络陷入了局部最优，而本文算法没有出现陷入局部最优的情况。只通过收敛性并不能全面地比较两种算法的好坏，下面对两种算法的精度和稳定性进行对比，采用平均相对误差(mean relative error, MRE)和最小误差平方和(least square estimate, LSE)来作为算法的精度和稳定性的评价指标。两种指标的计算公式为：

图3 两种算法的收敛性对比

(10)

(11)

式中:D为用于验证的信息数据样本量;ARe为融合算法得到的第e个融合后信息;AMe为第e个真实的诊断信息。通过计算得到两种算法的误差对比如表4所示。

表4 两种算法的误差对比

从MRE值可以看出，本文的数据融合算法的精度为88.82%，传统的BP神经网络数据融合的精度为81.05%，提高了7.77个百分点。通过比较两种算法的LSE值可知，本文数据融合算法的稳定性比传统BP神经网络数据融合提高了31.52% 。

数据融合完成后，采用上述灰色GM(1,1)模型对食品、饮料和烟酒制造行业后6个月的用电量进行预测，然后与直接用灰色GM(1,1)模型进行预测的结果进行对比。对预测结果进行记录，可以得到表5所示的预测结果对比数据。

表5 预测结果对比数据

从表5中数据可以看出，进行数据融合后的预测结果比直接预测的结果更准确。为了更好地表现两者之间的差距，对比预测的结果与真实值计算预测的误差率，误差率(w)的计算公式为：

(12)

通过计算，可以得到图4所示的预测误差率对比图。

图4 预测误差率对比图

从图4中可以看出，两种预测方式均存在波动性。但是总体来说先进行数据融合再进行预测的结果要比直接预测的结果误差要小，计算6次误差的平均值，先数据融合再进行预测的误差率相比直接预测的误差率降低了约1.495个百分点。

4 结束语

针对淮安市区域用电问题，提出了基于泛在物联网的用电行为解析架构，该架构能够联系各个地区的用电智能终端、传感器和物联网等，获取不同地区和范围的用户用电。通过淮安市区域用电总体情况以及淮安典型行业年用电特性分析，得到淮安用电的综合情况。结合基于统计学原理的大数据分析技术以及灰色GM(1，1)模型的大数据分析技术，实现了不同用户用电不同方式的分析。但是本文也存在一些不足，需要进一步地挖掘和研究。