基于新型双矢量模型预测的永磁同步电机控制

孙元杰， 周士贵， 张可程

(1.曲阜师范大学 工学院，山东 日照 276800;2.日照东方电机有限公司，山东 日照 276800)

0 引 言

随着永磁同步电机(permanent magnet synchronous motor, PMSM)在伺服系统中的广泛应用，模型预测控制以控制器设计简单和动态相应好等优点被广泛应用于电机的控制系统中。根据在一个控制周期内参与调整的基本电压矢量个数不同，可分为单矢量模型预测控制、双矢量模型预测控制和多矢量模型预测控制[1-2]。单矢量模型预测控制，稳态性能差，转矩脉动过大[3]。为此，文献[4]将占空比引入到模型预测控制中，在每个周期内选则两个电压矢量，第二个为零电压矢量，并且占空比的计算总是在选择最优电压矢量之后，因此不能保证选择的电压矢量最优，仍有电流波动。文献[5]采用两次电压矢量选择，选择的电压矢量为任意幅值和方向，并且考虑了作用时间对电压矢量选择的影响。文献[6]将电压误差引入到目标函数中，在选择出第一个电压矢量后，根据第一个电压矢量选择第二个电压矢量，此方法使算法的复杂度和计算量大为减少。

为减少计算量和电流的脉动，本文通过无差拍控制的思想以电压重新构造最优函数，通过设定预选集来选取最优电压矢量，最后根据调制模型的原理计算各电压矢量作用的时间。该方法与单矢量模型预测控制相比减少了电流的脉动，与传统占空比调制模型预测控制相比减小了算法的计算量和复杂度。最后通过试验，验证了该新型双矢量模型预测控制的有效性，减小了电流脉动，同时提高了系统的动态性能。

1 PMSM数学模型

假设不计电机中的漏电感、铁芯的涡流损耗且电机的绕组成对称分布等理想的条件下，永磁同步电机在同步旋转坐标系dq轴下的电流方程为：

(1)

式中：ud、uq为定子电压dq轴分量；id、iq为定子电流dq轴分量；Ld、Lq为dq轴电感；Rs为定子电阻；ψr为永磁体磁链；ω为电动机电角速度。

由于电机的控制周期远小于电机的机械时间常数，因此认为电机的速度采样周期没发生变化，即ωk=ωk+1。通过前向欧拉逼近代替负载电流导数di/dt，即通过式(2)逼近导数：

(2)

式中：Ts为电机控制系统的采样时间；ik+1为预测的下一个时刻的定子电流值；ik为当前时刻的电流采样值。

结合式(1)和式(2)得到离散的电流方程为：

(3)

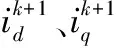
2 传统的模型预测控制

模型预测的控制框图如图1所示。在模型预测控时，首先获取三相电流经过Clarke和Park得到dq轴的电流;然后根据离散的dq坐标下的PMSM离散的电流预测模型，得到下一时刻预测的dq轴电流;再根据预测的dq轴电流进行滚动优化计算，选择出使目标函数值最小的电流值对应的电压矢量;最后根据选择的电压矢量选择相应的逆变器各开关器件的开关状态，进而控制PMSM。

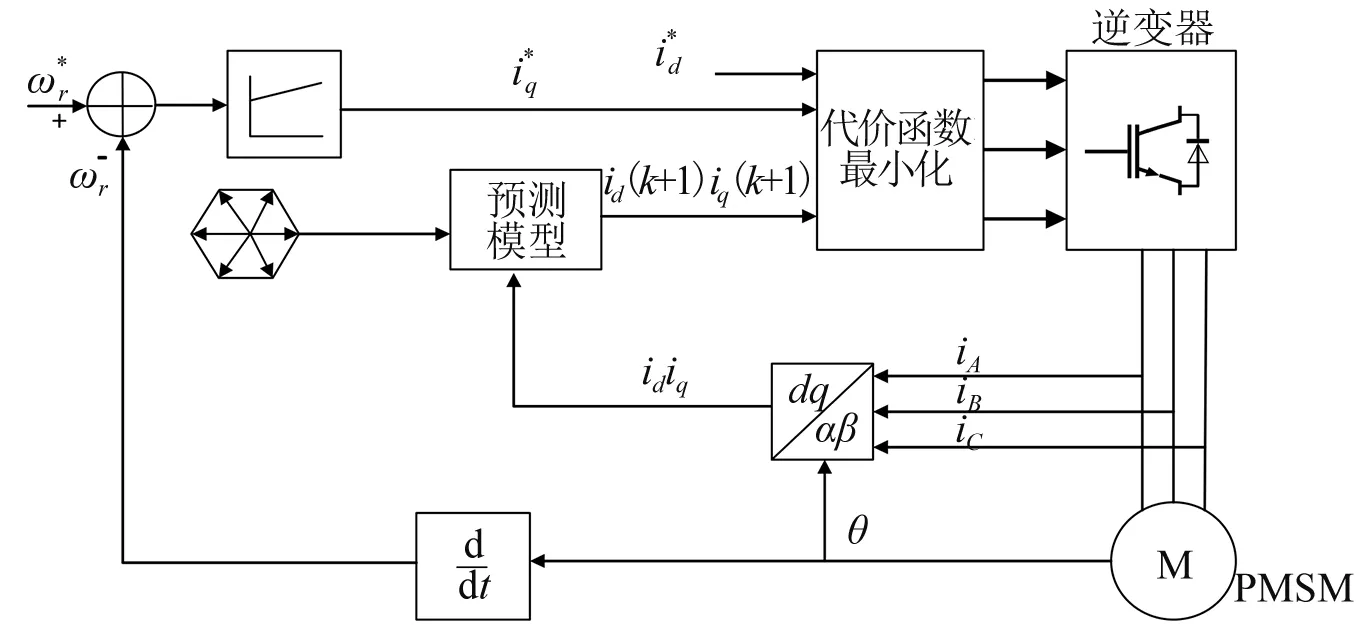
图1 模型预测控制框图

目标函数主要包含：使d轴电流最小，接近给定值0，对于PMSM来说，此时的转矩电流比最大；使q轴电流接近给定值，对iq实现精确快速跟踪；限制定子电流幅值，避免定子电流超过最大值，烧坏电机。为了达到控制目标，将目标函数设置为：

(4)

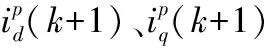
(5)

式中：f为非线性函数；idmax、iqmax为dq轴的最大电流值。

由逆变器的开关状态可知共有8中开关状态，包括6种有效电压输出状态，2种无效电压输出状态，如图2所示。电压矢量依次代入式(3),得到相应的预测电流。将预测的电流依次代入目标函数式(4)，滚动优化，将预测的下一时刻电流与给定的电流进行比较选择出误差最小的预测电流，然后将此电流值对应的逆变器开关状态作用于电机。如图3所示,S3所对应的电流与给定电流iref之间的误差最小，对应的目标函数的值最小，因此选用S3对应的逆变器开关状态作用于电机。

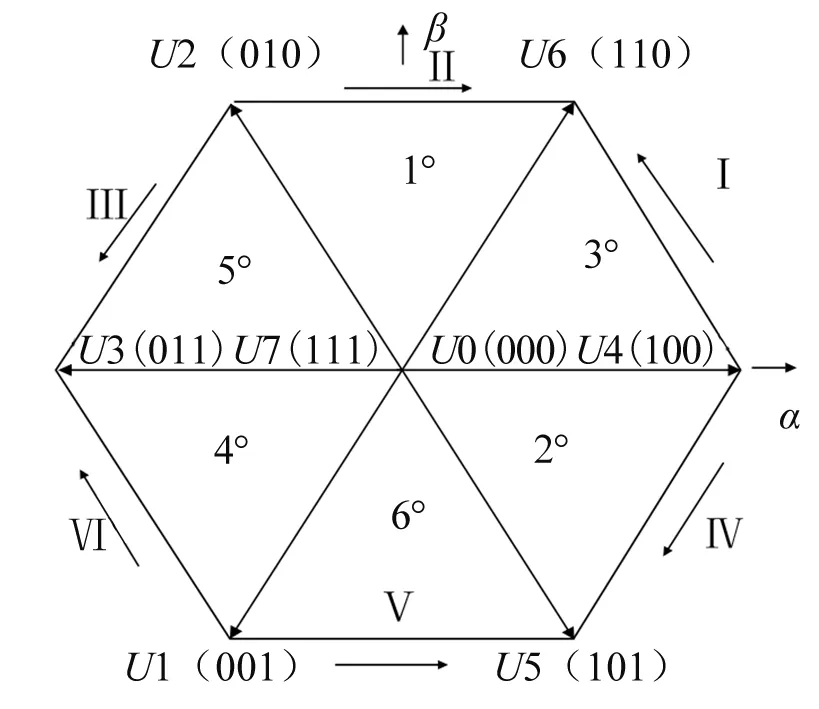
图2 基本电压空间矢量图

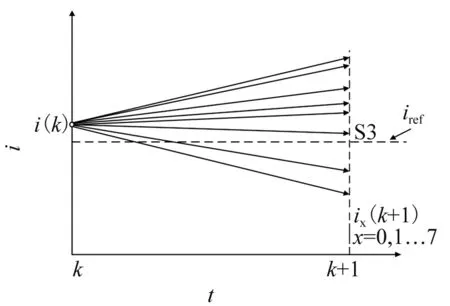
图3 电流矢量选择图

3 改进的双矢量模型预测控制

传统的单矢量模型预测电流含有的谐波大。而传统的双矢量控制中，在对最优电压选择时需要对最优的电流进行预测，由于是双矢量控制，因此在一次最优选择时就需要进行14次的电流预测计算，这样会大大增加计算的时间。为了简化算法，实现优良的控制效果,本文提出了改进的双矢量模型预测控制的方法。根据无差拍控制的思想通过式(3)可以得到目标电压方程。

(6)

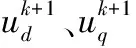
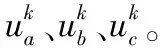
(7)

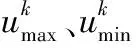
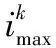
表1 预选矢量表

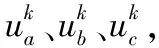
(8)

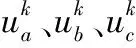
在通过目标函数选择出最优电压矢量后，需要对选择出的电压矢量计算各自作用的时间。根据调制模型预测控制的原理得到的各电压矢量中每一个电压矢量作用的时间为：

(9)

式中：t1为第一个电压矢量作用的时间;t2为第二个电压矢量作用的时间；g1为第一个电压矢量对应的最优函数;g2为第二个电压矢量对应的最优函数。

根据调制模型预测和电压矢量的关系，在得到各个电压矢量的组合之后各自作用的时间，将其合成新的电压矢量，具体公式如下：

U=(t1u1+t2u2)/TS

(10)

式中：u1为电压矢量组合中第一个电压矢量;u2为电压矢量组合中第二个电压矢量。然后用上述预选集中选择的电压矢量，通过上式合成的新电压矢量依次代入到电压最优函数中，选择一个使电压最优函数值最小的电压矢量组合作为电机控制中下一个周期的电机的电压矢量组合，从而实现电机高效、高性能的转动。

综上所述，改进的算法实现过程如下：①首先采集三相电流和三相电压，将采集的电压和电流进行大小判断，根据所判断的电流电压的大小选择相应的扇区；②根据扇区所对应的预选集分别代入式(8)中，选出使最优函数最小的电压矢量；③根据调制模型预测控制的原理，计算电压矢量作用的时间t1、t2，再根据式(10)合成新的电压矢量；④将合成的电压矢量再次代入到式(8)中选择出使最优函数值最小的电压矢量，作为逆变器的电压矢量值。

4 结果分析

为验证模型预测电流控制的有效性，按照图4搭建了PMSM的调速控制系统试验平台。试验采用TMS320F28335型号的DSP作为整个系统的控制单元进行算法的验证对比。PMSM的参数如下：Rs=0.17 Ω，Ld=Lq=0.78 mH,ψr=0.012 Wb，额定转速3 000 r/min，额定功率0.75 kW。对传统模型预测控制算法和新型双矢量模型预测控制算法进行了试验研究分析。

图4 永磁同步电机试验平台

第一组试验为电流环试验，比较传统模型预测控制器和新型双矢量模型预测控制器的电流跟踪情况。将电机转子固定，q轴给定电流在t1时刻从0 A阶跃上升为1 A。图5(a)为传统模型预测控制器下的电流跟踪情况。图5(b)为新型双矢量模型预测控制下的电流跟踪情况，纵坐标每小格为2 A。可以看到q轴反馈值快速达到给定值，采用新型双矢量模型预测控制电流的跟踪情况较好，响应快速。

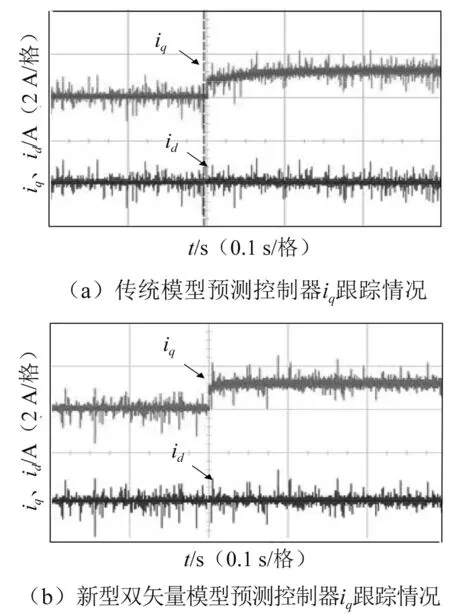
图5 d/q轴电流跟随情况(上q轴，下d轴)

第二组试验为减载试验。电机带2 N·m负载启动运行，稳定运行后，在t1时刻减小负载到1 N·m。图6为两种控制算法的电磁转矩波形，纵坐标每一小格为0.5 N·m，横坐标每一小格代表1 s。图7为转矩动态响应，纵坐标每一小格为0.5 N·m，横坐标每一小格为0.5 s。图7传统控制算法下，响应时间大约为500 ms。图7本文控制算法下，响应时间大约为300 ms，相比之下，新型双矢量模型预测控制拥有更快的响应速度，转矩波动小。

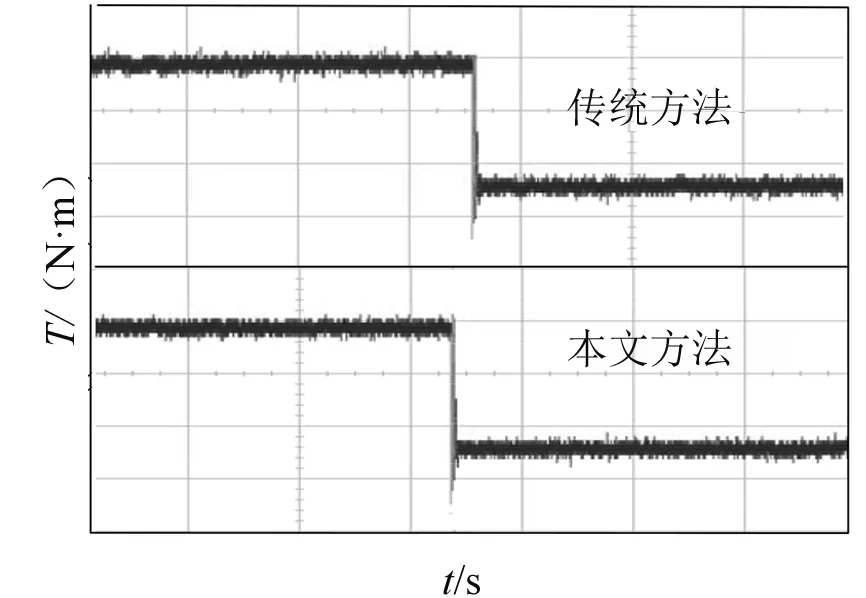
图6 电磁转矩波形

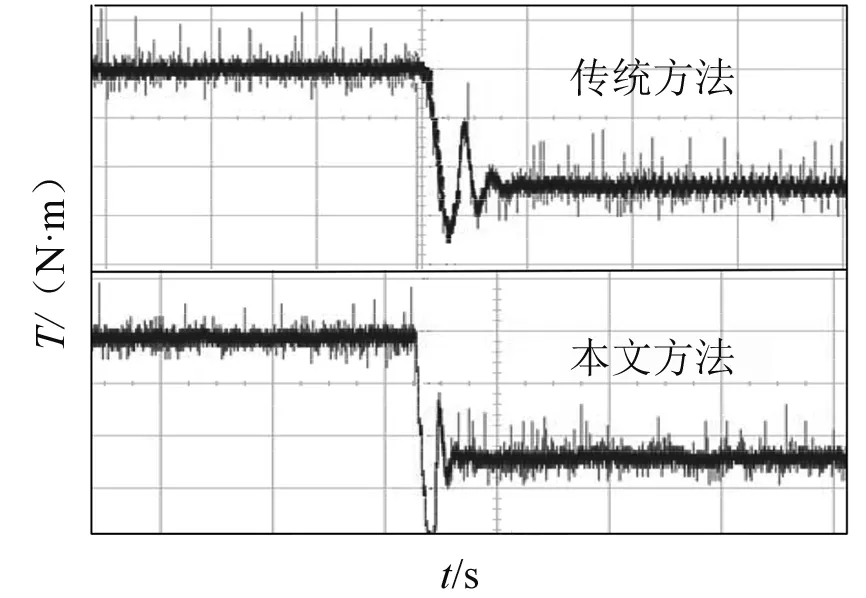
图7 动态响应时间

5 结束语

本文对模型预测控制进行分析，提出了一种改进的双矢量模型预测控制策略。该方法与传统的单矢量法相比大大地减小了电流谐波，与传统的双矢量法相比提高了逆变器的开关频率和开关器件的损耗，降低了模型预测算法的计算算量，使代码简化。通过试验验证了本文所提出的控制策略的有效性。