直升机双速传动系统低速挡动力学建模与特性分析

陈志刚，谢峰，刘志辉

(1.邵阳学院 机械与能源工程学院，湖南 邵阳，422000；2.邵阳学院 高效动力系统智能制造湖南省重点实验室，湖南 邵阳，422000)

直升机拥有良好的机动能力与垂直起降的性能，因此,被广泛应用于治安巡查、紧急救援、侦察运输等国民经济领域和国防建设领域中。为了提升直升机的性能，美国率先引入了一种双速传动系统[1]，该系统由两对齿轮副、超越离合器和摩擦离合器组成。随着直升机的飞跃发展，各种直升机事故也引起了人们的高度重视，研究表明，事故与传动系统有着密切关系，传动系统作为直升机的关键部件，其良好的动力学特性是直升机实现空中悬停、低速航行等行为最为重要的性能保障。关于直升机双速传动系统的研究文献较少，STEVENS等[2]提供了一种比较典型的双速传动系统的概念模型。国内针对汽车双离合自动变速器的动态特性展开了相关研究[3-5]，但暂未有专门针对直升机双速系统动态特性分析的相关文献。

当双速传动系统处于低速挡时，系统本质上是超越离合器与两级直齿轮传动副耦合的转子系统，系统的动力学模型见图1。齿轮传动系统动力学特性的研究一直是传动系统的研究热点[6-7]，在研究过程中，首先，需要建立系统的动力学模型。目前的动力学模型主要有集中参数模型、有限元模型、数学模型等，建模时，主要考虑时变啮合刚度、齿侧间隙等非线性因素。然后，应用Runga-Kutta法、集中参数法等方法对系统模型进行求解，得到齿轮系统的分岔、混沌等非线性特性[8-10]。对于超越离合器的动力学行为研究主要集中在与其工作环境下相对应的结构设计和可靠性分析，应力接触、疲劳寿命及过载能力分析等方面[11-13]。

虽然超越离合器与齿轮副组成的耦合系统已在汽车、船舶、直升机等领域应用广泛，但就此类系统的非线性特性研究并不多见，GILL-JEONG[14]研究了超越离合器与1对齿轮耦合的传动系统，建立了三自由度动力学模型；LEWICKI等[15]考虑了齿轮、离合器、轴的摩擦、扭转等因素，建立了系统的六自由度模型；王鹏等[16]综合考虑了齿侧间隙、啮合刚度等因素，建立了含超越离合的单对齿轮传动系统的非线性动力学模型；刘延伟等[17]以现有动力学模型为基础，建立了含转角补偿的超越离合器-齿轮系统动力学模型。

由以上分析可知，在研究过程中，中间连接轴扭转刚度这一参数对传动系统的影响规律未被深入探讨。为了探明直升机双速传动系统低速挡的振动机理，本文建立了考虑齿轮啮合刚度、啮合阻尼、离合器扭转刚度、扭转阻尼、中间连接轴扭转刚度、扭转阻尼等多种因素的五自由度动力学模型，运用Runga-Kutta法对系统进行求解，研究了两根中间连接轴扭转刚度对齿轮副动态传递误差、动载系数以及超越离合器动态滑溜角的影响，研究成果可为后续对此类双速传动系统的动态设计和优化提供参考，为提升直升机的机动性和经济性提供理论基础。

1 双速系统低速挡动力学模型

双速系统低速挡动力学模型见图1。

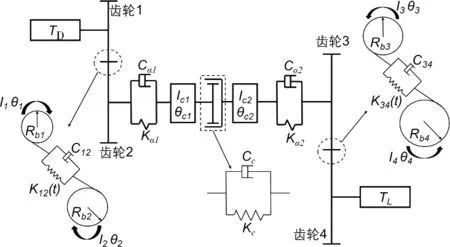
图1 双速系统低速挡动力学模型Fig.1 Low-speed gear dynamic model of the two-speed system

图1中，Rbi，Ii和θi(i=1，2，3，4)分别表示齿轮1，2，3和4的基圆半径、转动惯量与扭转位移；k12(34)(t)表示2对齿轮副的时变啮合刚度；Ici和θci(i=1，2)分别表示超越离合器主动端和从动端的转动惯量与扭转位移；Cαi和kαi(i=1，2)分别表示输入和输出2根中间连接轴的阻尼系数以及扭转刚度；kc表示超越离合器的扭转刚度；Cc表示超越离合器的扭转阻尼；bi(i=1，2)表示2对啮合齿轮齿侧间隙的一半；e12(34)(t)分别表示2对啮合齿轮的综合齿频误差，是以啮合齿频ωi(i=1,2)作为变化频率的周期函数，如式(1)所示；TD和TL表示作用在齿轮1上的驱动转矩和齿轮4输出的负载扭矩；TC表示超越离合器的转矩，如式(2)所示，其中a=1.5，b=1，c=0.25；f(x)表示具有齿侧间隙时齿轮副啮合力的非线性函数，如式(3)所示；C12(34)表示2对齿轮啮合的阻尼系数，如式(4)所示，其中，ζ1(2)表示齿轮副啮合阻尼比。

e12(34)(t)=eaicos(ωit+φhi)(i=1,2)

(1)

(2)

(3)

(4)

在进行动力学分析之前，首先做出假设：①2对齿轮副的齿轮都是未经修形的直齿轮；②离合器中所有斜撑块受载均匀，在楔合和脱开的过程中与内、外环无相对滑动；③忽略输入轴和输出轴的扭转、弯曲等变形；④视超越离合器的内、外环为弹性体，斜撑块为刚体。运用集中参数法、牛顿定律，可推出式(5)所示的五自由度运动微分方程:

(5)

定义齿轮1，2，3和4在啮合线上的位移分别为x1，x2，x3和x4，定义离合器主、从动端在啮合线上的位移分别为xc1和xc2，则有：x1=Rb1θ1；x2=Rb2θ2；x3=Rb3θ3；x4=Rb4θ4；xc1=Rb2θc1；xc2=Rb3θc2。引入齿轮副传动误差q，如式(6)所示，则q1，q2，q3，q4和qc分别表示齿轮1与齿轮2、齿轮3与齿轮4、齿轮2与离合器主动端、离合器从动端与齿轮3、超越离合器主、从动端的相对位移。简化方程组(5)，得到式(7):

(6)

(7)

式中：M1=m1m2/(m1+m2)，为齿轮副1的等效质量；M2=m3m4/(m3+m4)，为齿轮副2的等效质量；M2，c1=m2mc1/(m2+mc1)，为齿轮2与离合器主动端的等效质量；Mc2，3=mc2m3/(mc2+m3)，为离合器从动端与齿轮3的等效质量。

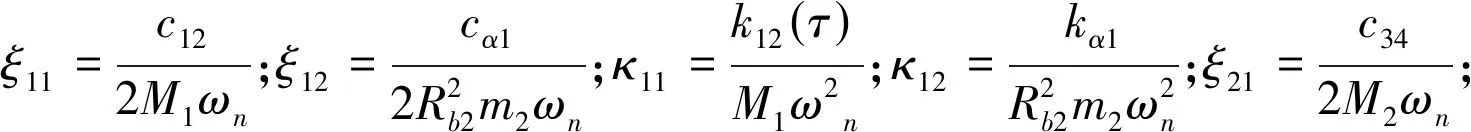
定义量纲一时间尺度τ=tωn与位移尺度bc，可将式(7)转换为量纲一化方程，如式(8)所示：

(8)

2 参数研究

传动系统的基本参数见表1，采用Runga-Kutta法对方程组进行求解，以中间连接轴1和中间连接轴2之间的扭转刚度比值为控制参数，研究齿轮副的动态传递误差、动载荷、超越离合器动态滑溜角随比值所产生的变化规律。

表1 含超越离合器的两级齿轮属性Table 1 Specifications of two-stage gear with one-way clutch

为研究对齿轮副的动态传递误差和超越离合器的动态滑溜角的影响规律，可采用均方根值(EDT)和均方根值误差(oscillating DTE,EODT)对影响规律进行描述，如式(9)和(10)所示：

(9)

(10)

为研究控制参数对齿轮在工作过程中所允许的最大啮合力的影响规律，可采用动载系数KV对影响规律进行描述，如式(11)所示：

(11)

2.1 齿轮副特性分析

输出端中间连接轴的扭转刚度与输入端中间连接轴的扭转刚度之间的比值为Ω。图2(a)～(c)所示分别为齿轮传动副1在不同中间连接轴扭转刚度比下的EDT响应、EODT响应和动载系数Kv。从图2(a)可以看到：当比值Ω≤2.5时，响应曲线存在明显的跳跃现象并达到最大值；当Ω≥2.5时，传递误差只在小幅度范围波动。从图2(b)可以看出:当Ω≤2.5时，存在明显的跳跃现象，波动范围大且有多处突变；当Ω≥2.5时，继续增加比值能够有效抑制齿轮在运转过程中产生的振动和噪声。由图2(c)可知:在Ω≤2.5的范围内，齿轮所承受的最大动载荷达到峰值；当Ω≥2.5时，随着比值的增加，能有效减小齿轮承受的最大动载荷。

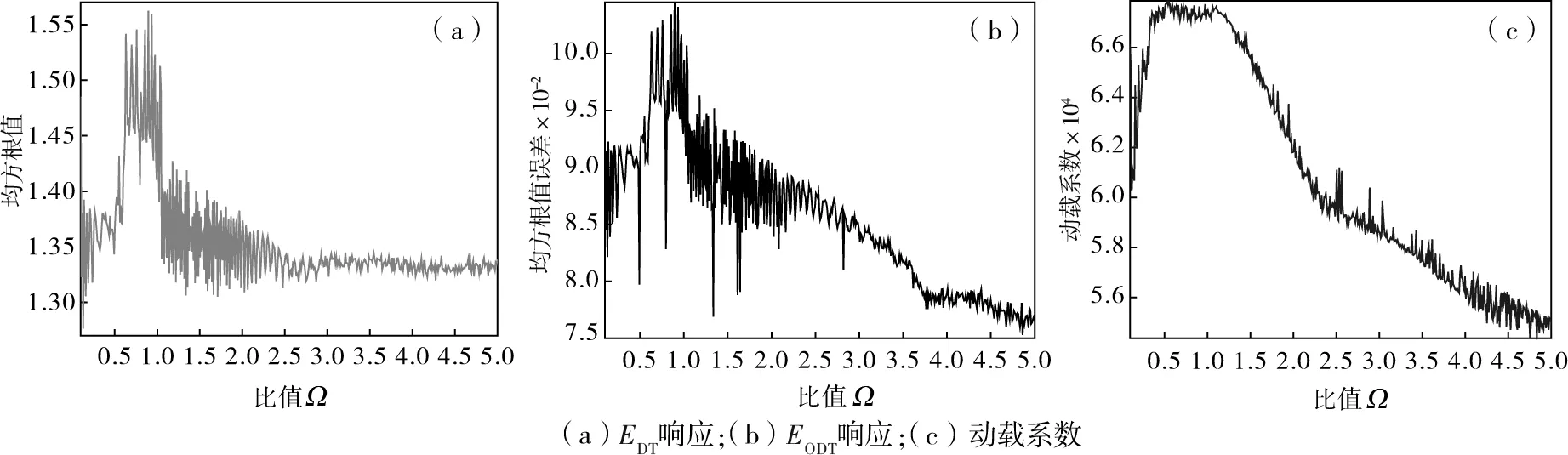
图2 不同Ω下齿轮传动副1的EDT响应、EODT响应、动载系数Fig.2 Traces of EDT response,EODT response and dynamic load coefficient of Gear Pair 1 with different Ω

图3(a)～(c)所示分别是齿轮传动副2在不同中间连接轴扭转刚度比下的EDT响应、EODT响应和动载系数KV。从图3(a)可以看出:当比值Ω≤2.5时，响应曲线呈规律的上下波动，随着输出轴扭转刚度的递增，波动范围逐渐递减；当Ω≥2.5时，传递误差均方根值基本维持在一恒定值，只存在小幅度波动。由图3(b)可知:当比值Ω较小时，存在明显的非线性跳跃现象；当比值Ω较大时，曲线波动幅度减小，齿轮副2产生的振动和噪声有所改善。由图3(c)可知:随着比值Ω的递增，齿轮副2所承受的最大动载荷减小。

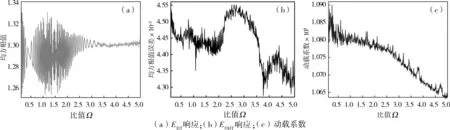
图3 不同Ω下齿轮传动副1的EDT响应、EODT响应、动载系数Fig.3 Traces of EDT response,EODT response and dynamic load coefficient of Gear Pair 2 with different Ω

2.2 超越离合器动态滑溜角分析

当超越离合器处于工作状态时，若要实现外环与内环的同步转动，则外环要比内环多转动一定角度，这个转角差被称为滑溜角。超越离合器接合后外、内环的瞬时转角差被称为动态滑溜角。图4(a)和4(b)所示分别表示超越离合器的动态滑溜角在不同中间连接轴扭转刚度比下的EDT响应和EODT响应。由图4(a)可知：当比值Ω≤2.5时，动态滑溜角随着比值的递增达到峰值，然后逐渐下降；当Ω≥2.5时，离合器的动态滑溜角基本保持恒定值。图4(b)说明了当扭转刚度比值Ω≥2.0时，随着比值的递增，离合器在运转过程中产生的振动和噪声得到有效的控制。

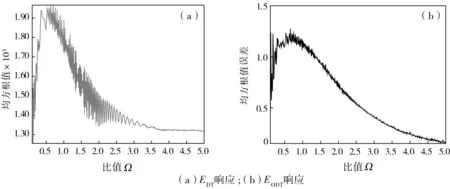
图4 不同Ω下超越离合器动态滑溜角的EDT响应、EODT响应Fig.4 Traces of EDT response,EODT response of the dynamic windup angle error of one-way clutch with different Ω

3 结论

本文在现有的基础上完善了超越离合器-两级齿轮传动系统的非线性动力学模型，通过研究中间连接轴扭转刚度之间的关系对系统动态性能的影响，得到以下结论：

1)当输出、输入两根中间连接轴扭转刚度之间的比值Ω≥2.5时，可以有效抑制齿轮副的动态传递误差，能够同时有效减小齿轮副所承受的最大动载荷，延长系统的使用寿命。

2)当Ω≥2.5时，继续增大输出端中间连接轴的扭转刚度，可以使超越离合器的动态滑溜角减小，提高系统的灵敏度。