四个平行共轴等大载流方线圈磁场的均匀性分析
昝会萍,张引科
(西安建筑科技大学 理学院,陕西 西安 710055)
匀强磁场在科学研究和工程领域有广泛应用[1,2].常用亥姆霍兹线圈在小区域产生近似均匀的磁场[3],该磁场在线圈轴线上线圈半径大小的范围内有大于5%的起伏[4].昝会萍等[5,6]及曾晓英[7]提出了用3个平行共轴圆线圈产生匀强磁场的设想,3线圈系统的磁场在轴线上线圈半径范围内的起伏小于1%.郑珂等[8]与赵立强等[9]提出了方形亥姆霍兹线圈方案,当2个线圈之间的距离是线圈边长的0.5445倍时,在线圈中心附近沿线圈轴线方向0.343倍线圈边长、垂直线圈轴线方向0.384倍线圈边长的区域内,磁感应强度的相对偏差小于1%;在轴线方向0.190倍线圈边长、垂直线圈轴线方向0.222倍线圈边长的区域内,磁感应强度的相对偏差小于1‰[10].吴亚冬等[11]提出了用3个平行共轴方线圈产生匀强磁场的方法.本文建立了4个平行共轴等大载流方线圈磁场磁感应强度的表达式,得出了系统磁场均匀性最好的条件,对系统在3种具体情况下形成磁场的均匀性进行了分析.与方形亥姆霍兹线圈的磁场相比,4个平行共轴等大载流方线圈的磁场均匀性更好、均匀区域范围更大.
1 4个平行共轴等大载流方线圈的磁场
图1所示为4个平行共轴等大载流方线圈,它由4个边长均为2a的方线圈组成,方线圈平行于坐标系的xOy坐标面、中心在z轴上、各边与x轴或y轴平行,中间两个线圈距离xOy坐标面均为d1、电流强度为I1,左右两个线圈距离xOy坐标面均为d2、电流强度为I2.
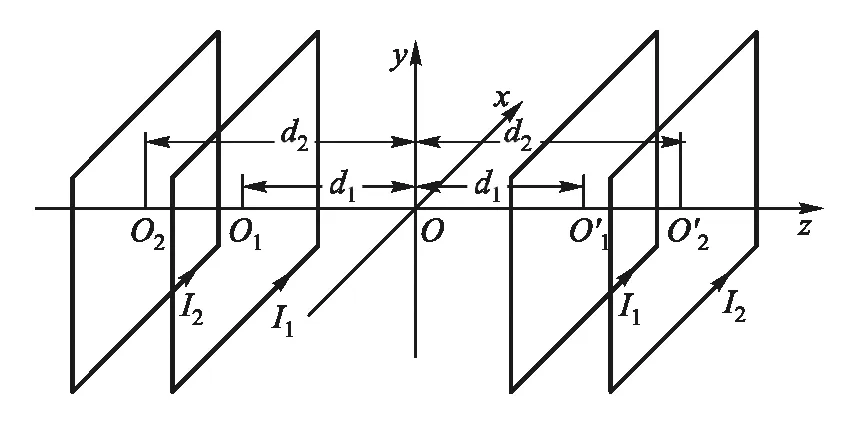
图1 4个平行共轴等大载流方线圈
根据磁场叠加原理及方形亥姆霍兹线圈磁感应强度的表达式,4个平行共轴等大载流方线圈磁感应强度的3个分量分别是:
Bfx(x,y,z)=Btx(I1,d1;x,y,z)+
Btx(I2,d2;x,y,z)
(1)
Bfy(x,y,z)=Bty(I1,d1;x,y,z)+
Bty(I2,d2;x,y,z)
(2)
Bfz(x,y,z)=Btz(I1,d1;x,y,z)+
Btz(I2,d2;x,y,z)
(3)
在这3式中,Btx(I,d;x,y,z),Bty(I,d;x,y,z)和Btz(I,d;x,y,z)分别是边长为2a、间距为2d、电流强度为I的正方形亥姆霍兹线圈磁感应强度的3个分
量,具体表达式参见文献[12]中的式(1)—式(3).在z轴上的各点,4个线圈的磁场只有z分量,磁感应强度为
(4)
其中
(5)
坐标原点(即线圈系统中心)的磁感应强度为
(6)
2 4个平行共轴等大载流方线圈形成匀强磁场的条件
4个平行共轴等大载流方线圈轴线上磁感应强度函数Bfz0(z′)是z′的偶函数.为了使线圈系统中心区域的磁场均匀性最好,可以使Bfz0(z′)对z′的低次偶数阶导数在z′=0处的值等于零,由此确定参量α1,α2和β的取值,进而得到4个方线圈形成最均匀磁场时线圈中的电流及线圈之间的距离必须满足的关系,这就是4个平行共轴等大载流方线圈形成匀强磁场的条件.把函数Bfz0(z′)在z′=0处用泰勒级数展开,有
(7)
式中,Bfz0(z′)对z′的二阶导数、四阶导数和六阶导数在z′=0处的值分别是
(8)
(9)
(10)
式中
(11)
(12)
(13)
2.1 均匀性较低磁场的形成条件
为了使线圈中心区域磁场的均匀性较好,使Bfz0(z′)对z′的二阶导数在z′=0处值等于零,即
g1(α1)+βg1(α2)=0
(14)
显然
(15)
式(14)就是线圈系统在中心区域形成均匀性较低磁场的条件,在其满足的情况下,线圈系统中心区域内z轴方向的磁感应强度分量表示为
(16)
其中
(17)
(18)
从数学上看,式(14)是关于α1、α2和β的超定方程,一般有无数组解.对于所研究的问题,可以要求β>0及α2>α1,考虑到函数g1(α)的特点,α1和α2的解存在区间分别是(0,0.5445)和(0.5445,+∞).表1和表2分别给出了用数值方法在电流相等和线圈间距相等两种特殊条件下得到的式(14)的几组解,也就是这两种条件下线圈系统产生均匀性较低磁场时α1,α2和β的几组取值.

表1 电流相同(即β=1)的4个线圈产生均匀性较低磁场时α1和α2的几组取值

表2 间距相等(即α2=2α1)的4个线圈产生均匀性较低磁场时α1和β的几组取值
2.2 均匀性较高磁场的形成条件
为了使线圈中心区域磁场的均匀性更佳,使Bfz0(z′)对z′的二阶导数和四阶导数在z′=0处的值同时等于零,也就是
g1(α1)+βg1(α2)=0
(19)
g2(α1)+βg2(α2)=0
(20)
显然
(21)
式(19)和(20)就是线圈系统在中心区域形成较高均匀性磁场的条件,在其满足的时,线圈系统中心区域z轴方向的磁感应强度分量可以表示为
(22)
其中
(23)
(24)
表3给出了4个平行共轴等大载流方线圈产生均匀性较高磁场时α1,α2和β的几组取值.

表3 4个平行共轴等大载流方线圈产生均匀性较高磁场时α1、α2和β的几组取值
3 4个平行共轴等大载流方线圈磁场的均匀性分析
采用磁感应强度相对偏差EB(x,y,z)描述磁场的均匀性,EB(x,y,z)定义为
(25)
它描述磁感应强度B(x,y,z)对磁感应强度B(0,0,0)偏离的相对程度.
3.1 电流相同或间距相等的4个线圈产生的均匀性较低磁场分析
图2给出了电流相同的4个线圈产生的均匀性较低磁场在xOz坐标面上的分布.此时,3个参量的取值分别是α1=0.4500,α2=1.4144和β=1.可以看出,xOz坐标面上,相对于线圈系统中心点的磁感应强度,在|x|<0.35a及|z|<0.7a的范围内,磁感应强度x分量的起伏小于5%、z分量的起伏小于1%,磁场的均匀性总体较低.在|x|<0.35a及|z|<0.4a的范围内,磁感应强度的相对偏差小于1%、磁场与z轴的夹角小于1度,磁场的均匀性较低;在|x|<0.2a及|z|<0.22a的范围内,磁感应强度的相对偏差小于0.1%、磁场与z轴的夹角小于0.1度,磁场的均匀性较高;在|x|<0.11a及|z|<0.13a的范围内,磁感应强度的相对偏差小于0.01%、磁场与z轴的夹角小于0.01度,磁场的均匀性极高.
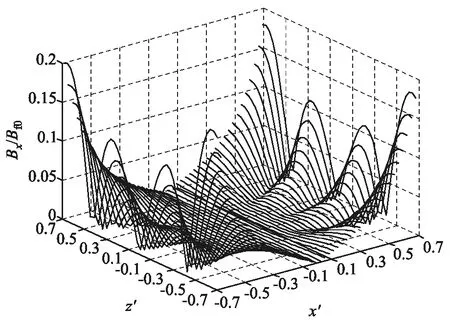
(a) | Bx|/Bf00m的分布
图3是间距相等的4个线圈产生的均匀性较低磁场在xOz坐标面上的分布.此时,3个参量的取值分别是α1=0.3500、α2=0.7000和β=2.1695.可以发现,xOz坐标面上,相对于线圈系统中心点的磁感应强度,在|x|<0.2a及|z|<0.7a的范围内,磁感应强度x分量的起伏小于5%、z分量的起伏小于1%,磁场的均匀性总体较低;在|x|<0.32a及|z|<0.38a的范围内,磁感应强度的相对偏差小于1%、磁场与z轴的夹角小于1度,磁场的均匀性较低;在|x|<0.18a及|z|<0.2a的范围内,磁感应强度的相对偏差小于0.1%、磁场与z轴的夹角小于0.1度,磁场的均匀性较高;在|x|<0.13a及|z|<0.11a的范围内,磁感应强度的相对偏差小于0.01%、磁场与z轴的夹角小于0.01度,磁场的均匀性极高.
3.2 4个线圈产生的均匀性较高磁场分析
图4为4个线圈产生的均匀性较高磁场在xOz坐标面上的分布.此时,3个参量的取值分别是α1=0.2500、α2=0.9966和β=2.4033.可以发现,在xOz坐标面上,相对于线圈系统中心点的磁感应强度,在|x|<0.3a及|z|<0.7a的范围内,磁感应强度x分量的起伏小于1%、z分量的起伏小于1%,磁场的均匀性总体较高.在|x|<0.53a及|z|<0.63a的范围内,磁感应强度的相对偏差小于1%、磁场与z轴的夹角小于1度,磁场的均匀性较低;在|x|<0.4a及|z|<0.5a的范围内,磁感应强度的相对偏差小于0.1%、磁场与z轴的夹角小于0.1度,磁场的均匀性较高;在|x|<0.3a及|z|<0.35a的范围内,磁感应强度的相对偏差小于0.01%、磁场与z轴的夹角小于0.01度,磁场的均匀性极高.可见,4线圈磁场无论在均匀性还是在方向性方面,都明显优于方形亥姆霍兹线圈磁场.
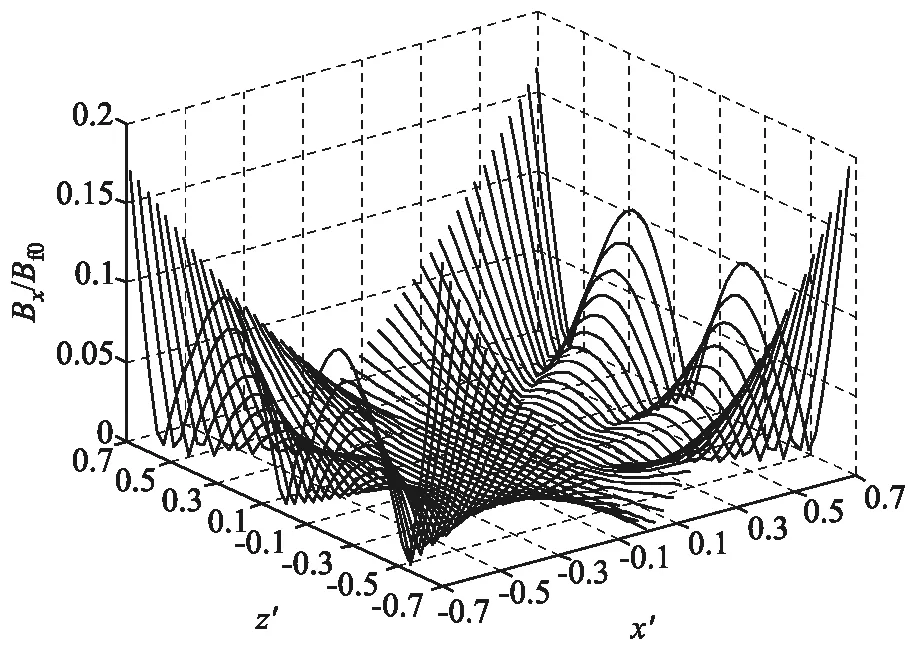
(a) |Bx|/Bf00m的分布
4 结论
用4个平行共轴等大载流方线圈在小区域产生匀强磁场的方法简单易行,对4线圈系统在3种具体情况下磁场均匀性的分析表明,建立的4线圈系统磁感应强度表达式和产生均匀性最佳磁场的条件是正确的和可行的.主要结论有:1)在最佳条件下,4个平行共轴等大载流方线圈在线圈中心区域内产生的磁感应强度对中心处磁感应强度的相对偏差与(z/a)6成正比.2)在最佳状态下,4线圈系统能够在大约|z|<0.35a及|x|<0.3a的范围内,产生磁感应强度相对偏差小于0.01%、磁场方向偏差小于0.01度的磁场.3)与方形亥姆霍兹线圈相比,四线圈的磁场在均匀性、方向性等方面都有明显优势.
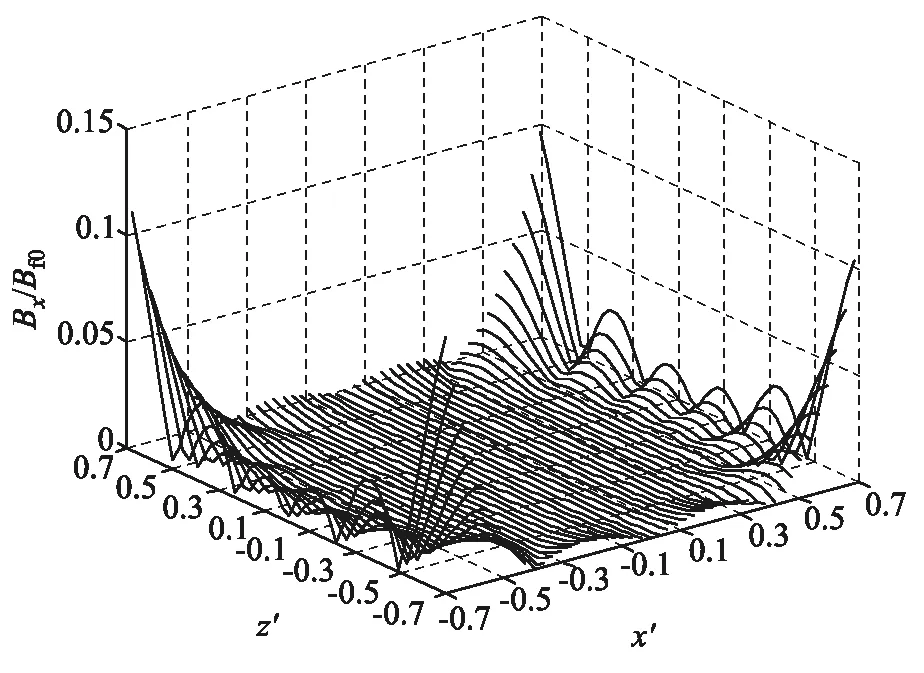
(a) |Bx|/Bf00m的分布

